MATLAB 状态空间设计 —— LQG/LQR 和极点配置算法
系列文章目录
文章目录
- 系列文章目录
- 前言
- 一、相关函数 —— LQG/LQR 和极点配置算法
- 1.1 LQR —— lqr 函数
- 1.1.1 函数用法
- 1.1.2 举例
- 1.1.2.1 倒摆模型的 LQR 控制
- 1.2 LQG —— lqg() 函数
- 1.2.1 函数用法
- 1.2.2 举例
- 1.3 极点配置 —— place() 函数
- 1.3.1 函数用法
- 1.3.2 示例
- 1.3.2.1 二阶系统的极点配置设计
- 1.3.2.2 极点配置观测器设计
前言
状态空间控制设计方法,如 LQG/LQR 和极点配置算法,适用于 MIMO 设计。
一、相关函数 —— LQG/LQR 和极点配置算法
1.1 LQR —— lqr 函数
1.1.1 函数用法
[K,S,P] = lqr(sys,Q,R,N)
[K,S,P] = lqr(A,B,Q,R,N)
说明
[K,S,P] = lqr(sys,Q,R,N)计算连续时间或离散时间状态空间模型sys的最优增益矩阵
K、相关代数黎卡提方程的解S和闭环极点P。Q和R分别是状态和输入的权重矩阵。交叉项矩阵N
在省略时设为零。
[K,S,P] = lqr(A,B,Q,R,N)使用连续时间状态空间矩阵A和B计算最佳增益矩阵K、相关黎卡提方程的解S以及闭环极点P。对于离散时间模型,请使用dlqr。
输入参数
sys- 动态系统模型,动态系统模型,以ss模型对象的形式指定。
A- 状态矩阵,状态矩阵,指定为n x n矩阵,其中n为状态数。
B- 输入到状态矩阵,输入 - 状态矩阵,指定为n x m的输入 - 状态矩阵,其中m为输入个数。
Q- 状态成本权重矩阵,状态-成本加权矩阵,指定为n x n矩阵,其中n为状态数。你可以使用 Bryson 规则来设置Q的初始值,其给定值为
Q i , i = 1 m a x i m u m a c c e p t a b l e v a l u e o f ( e r r o r s t a t e s ) 2 , i ∈ { 1 , 2 , . . . , n } Q_{i,i}=\dfrac{1}{\mathrm{maximum~acceptable~value~of~(error_{states})^{2}}},~\mathrm{i}\in\{1,2,...,n\} Qi,i=maximum acceptable value of (errorstates)21, i∈{1,2,...,n}
Q = [ Q 1 , 1 0 ⋯ 0 0 Q 2 , 2 ⋯ 0 0 0 ⋱ ⋮ 0 0 ⋯ Q n , n ] Q=\left[\begin{array}{c c c c}{{Q_{1,1}}}&{{0}}&{{\cdots}}&{{0}}\\ {{0}}&{{Q_{2,2}}}&{{\cdots}}&{{0}}\\ {{0}}&{{0}}&{{\ddots}}&{{\vdots}}\\ {{0}}&{{0}}&{{\cdots}}&{{Q_{n,n}}}\end{array}\right] Q=⎣⎢⎢⎢⎡Q1,10000Q2,200⋯⋯⋱⋯00⋮Qn,n⎦⎥⎥⎥⎤
R- 输入成本权重矩阵,输入成本加权矩阵,指定为标量或与D'D相同大小的矩阵。这里,D是馈通状态空间矩阵。可以使用 Bryson 规则设置R的初始值,其给定值为
R i , i = 1 m a x i m u m a c c e p t a b l e v a l u e o f ( e r r o r s t a t e s ) 2 , i ∈ { 1 , 2 , . . . , m } R_{i,i}=\dfrac{1}{\mathrm{maximum~acceptable~value~of~(error_{states})^{2}}},~\mathrm{i}\in\{1,2,...,m\} Ri,i=maximum acceptable value of (errorstates)21, i∈{1,2,...,m}
R = [ R 1 , 1 0 ⋯ 0 0 R 2 , 2 ⋯ 0 0 0 ⋱ ⋮ 0 0 ⋯ R n , n ] R=\left[\begin{array}{c c c c}{{R_{1,1}}}&{{0}}&{{\cdots}}&{{0}}\\ {{0}}&{{R_{2,2}}}&{{\cdots}}&{{0}}\\ {{0}}&{{0}}&{{\ddots}}&{{\vdots}}\\ {{0}}&{{0}}&{{\cdots}}&{{R_{n,n}}}\end{array}\right] R=⎣⎢⎢⎢⎡R1,10000R2,200⋯⋯⋱⋯00⋮Rn,n⎦⎥⎥⎥⎤
这里,m 是输入的个数。
N- 可选的交叉项矩阵,可选的交叉项矩阵,以矩阵形式指定。如果没有指定N,lqr默认将N设为 0。
输出参数
K- 最优增益,闭环系统的最优增益,以大小为n的行向量形式返回,其中n为状态数。
S- 相关代数黎卡提方程的解,相关代数黎卡提方程的解,以n x n矩阵形式返回,其中n为状态数。换句话说,S
的维度与状态空间矩阵A相同。更多信息,请参见 icare 和 idare。
P- 闭环系统的极点,闭环系统的极点,以大小为n的列向量形式返回,其中n为状态数。
局限性
输入数据必须满足以下条件:
-
一对矩阵 A 和 B 必须是可稳定的。
-
[ Q , N ; N ′ , R ] [Q,N;N',R] [Q,N;N′,R] 必须是非负定。
-
R > 0 R>0 R>0 并且 Q − N R − 1 N T ≥ 0. Q-N R^{-1}N^{T}\ge0. Q−NR−1NT≥0.
-
( Q − N R − 1 N T , A − B R − 1 N T ) (Q-N R^{-1}N^{T},\,A-B R^{-1}N^{T}) (Q−NR−1NT,A−BR−1NT) 在虚轴(或离散时间中的单位圆)上没有不可观测的模式。
提示: lqr 支持非奇异 E 的描述符模型。lqr 的输出 S 是等效显式状态空间模型的代数黎卡提方程的解: d x d t = E − 1 A x + E − 1 B u {\dfrac{d x}{d t}}=E^{-1}A x+E^{-1}B u dtdx=E−1Ax+E−1Bu
LQR 算法
对于连续时间系统,lqr 计算的状态反馈控制 u=-Kx 可使二次成本函数最小化
J ( u ) = ∫ 0 ∞ ( x T Q x + u T R u + 2 x T N u ) d t J(u)=\int_{0}^{\infty}(x^{T}Q x+u^{T}R u+2x^{T}N u)d t J(u)=∫0∞(xTQx+uTRu+2xTNu)dt 系统动力学
x ˙ = A x + B u . {\dot{x}}=A x+B u. x˙=Ax+Bu.除了状态反馈增益 K 之外,lqr 还返回相关代数黎卡提方程的解 S A T S + S A − ( S B + N ) R − 1 ( B T S + N T ) + Q = 0 A^{T}S+S A-(S B+N)R^{-1}(B^{T}S+N^{T})+Q=0 ATS+SA−(SB+N)R−1(BTS+NT)+Q=0 和闭环极点 P = eig(A-BK)。增益矩阵 K 由 S 得出,计算公式为
K = R − 1 ( B T S + N T ) . K=R^{-1}(B^{T}S+N^{T}). K=R−1(BTS+NT). 对于离散时间系统,lqr 可计算状态反馈控制 u n = − K x n u_{n}=-K x_{n} un=−Kxn
最小化 J = ∑ n = 0 ∞ { x T Q x + u T R u + 2 x T N u } J=\sum_{n=0}^{\infty}\{x^{T}Q x+u^{T}R u+2x^{T}N u\} J=n=0∑∞{xTQx+uTRu+2xTNu} 系统动力学
x n + 1 = A x n + B u n x_{n+1}=A x_{n}+B u_{n} xn+1=Axn+Bun在任何情况下,如果省略交叉项矩阵 N,lqr 都会将 N 设为 0。
1.1.2 举例
1.1.2.1 倒摆模型的 LQR 控制
pendulumModelCart.mat 包含小车上倒立摆的状态空间模型,其输出为小车位移 x 和摆角 θ,控制输入 u 为小车上的水平力。
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{bmatrix…
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \bm{y}=\begin{…
首先,将状态空间模型 sys 加载到工作区。
load('pendulumCartModel.mat','sys')
由于输出为 x x x 和 θ \theta θ,而输入只有一个,因此使用 Bryson 规则确定 Q 和 R。
Q = [1,0,0,0;...0,0,0,0;...0,0,1,0;...0,0,0,0];
R = 1;
使用 lqr 求增益矩阵 K。由于没有指定 N,lqr 将 N 设为 0。
[K,S,P] = lqr(sys,Q,R)
K = 1×4-1.0000 -1.7559 16.9145 3.2274S = 4×41.5346 1.2127 -3.2274 -0.68511.2127 1.5321 -4.5626 -0.9640-3.2274 -4.5626 26.5487 5.2079-0.6851 -0.9640 5.2079 1.0311P = 4×1 complex-0.8684 + 0.8523i-0.8684 - 0.8523i-5.4941 + 0.4564i-5.4941 - 0.4564i
虽然 Bryson 规则通常能提供令人满意的结果,但它通常只是根据设计要求调整闭环系统响应的试错迭代设计程序的起点。
1.2 LQG —— lqg() 函数
1.2.1 函数用法
reg = lqg(sys,QXU,QWV)
reg = lqg(sys,QXU,QWV,QI)
reg = lqg(sys,QXU,QWV,QI,'1dof')
reg = lqg(sys,QXU,QWV,QI,'2dof')
reg = lqg(___,'current')
[reg,info] = lqg(___)
说明
reg = lqg(sys,QXU,QWV)给定一个被控对象的状态空间模型sys以及权重矩阵QXU和
QWV,计算出一个最优线性二次高斯(LQG)调节器reg。动态调节器reg利用测量值y生成控制信号u,将
y调节到零值附近。使用正反馈将该调节器与被控对象的输出y连接起来。
LQG 调节器使成本函数最小化
J = E { * l i m τ → ∞ 1 τ ∫ 0 τ [ x T , u T ] Q x u [ x u ] d t } J=E\left\{\operatorname*{lim}_{\tau\rightarrow\infty}\frac{1}{\tau}\int_{0}^{\tau}[x^{T},u^{T}]Q x u\begin{bmatrix} x \\ u \end{bmatrix}d t\right\} J=E{*limτ→∞τ1∫0τ[xT,uT]Qxu[xu]dt}受被控对象方程的约束
d x / d t = A x + B u + w y = C x + D u + ν \begin{array}{c}{{d x/d t=A x+B u+w}}\\ {{y=C x+D u+\nu}}\end{array} dx/dt=Ax+Bu+wy=Cx+Du+ν
其中,过程噪声 w 和测量噪声 v 均为具有协方差的高斯白噪声:
KaTeX parse error: Undefined control sequence: \cal at position 95: …rime}]\right)={\̲c̲a̲l̲ ̲Q}{\cal W}V
reg = lqg(sys,QXU,QWV,QI)使用设定点指令r和测量值y来生成控制信号u。
LQG 伺服控制器可使成本函数最小化
J = E { * l i m τ → ∞ 1 τ ∫ 0 τ ( [ x T , u T ] Q x u ∣ u x ∣ + x i T Q i x i ) d t } J=E\left\{\operatorname*{lim}_{\tau\rightarrow\infty}\frac{1}{\tau}\int_{0}^{\tau}\left([x^{T},u^{T}]Q x u\biggl|_{u}^{x}\biggr|+x_{i}^{T}Q_i x_{i}\right)d t\right\} J=E{*limτ→∞τ1∫0τ([xT,uT]Qxu∣∣∣∣ux∣∣∣∣+xiTQixi)dt}
对于多输入多输出系统,
r、y和 x i x_i xi 的长度必须相同。
reg = lqg(sys,QXU,QWV,QI,'1dof')计算以e = r - y而不是[r ; y]
作为输入的一自由度伺服控制器。
reg = lqg(sys,QXU,QWV,QI,'2dof')等价于
LQG(sys,QXU,QWV,QI),并产生前面显示的二自由度伺服控制器。
reg = lqg(____,'current')使用 "current"卡尔曼估计器,该估计器在计算离散时间系统的 LQG
调节器时使用x[n|n]作为状态估计值。
[reg,info] = lqg(____)返回前面任何语法结构info
中的控制器和估计器增益矩阵。例如,您可以使用控制器和估计器增益以观测器形式实现控制器。更多信息,请参阅算法。
1.2.2 举例
线性-二次高斯 (LQG) 调节器和伺服控制器设计
本例介绍如何为以下系统设计线性二次高斯(LQG)调节器、一自由度 LQG 伺服控制器和二自由度 LQG 伺服控制器。

被控对象有三个状态 (x)、两个控制输入 (u)、三个随机输入 (w)、一个输出 (y)、输出的测量噪声 (v),以及以下状态方程和测量方程。
d x d t = A x + B u + w y = C x + D u + ν \dfrac{d x}{d t}=A x+B u+w \\ y=C x+D u+\nu dtdx=Ax+Bu+wy=Cx+Du+ν
A = [ 0 1 0 0 0 1 1 0 0 ] B = [ 0.3 1 0 1 − 0.3 0.9 ] \begin{array}{r l}{A={\left[\begin{array}{l l l}{0}&{1}&{0}\\ {0}&{0}&{1}\\ {1}&{0}&{0}\end{array}\right]}}&{{}B={\left[\begin{array}{l l}{0.3}& {1}\\ 0& 1 \\ {-0.3} &{0.9}\end{array}\right]}}\end{array} \\ A=⎣⎡001100010⎦⎤B=⎣⎡0.30−0.3110.9⎦⎤ C = [ 1.9 1.3 1 ] D = [ 0.53 − 0.61 ] C=\left[1.9\quad\ 1.3\quad\ 1\right]\quad D=\left[0.53-0.61\right] C=[1.9 1.3 1]D=[0.53−0.61]
系统的噪声协方差数据如下
Q n = E ( w w T ) = [ 4 2 0 2 1 0 0 0 1 ] Q n=E(w w^{T})=\left[{\begin{array}{c c c}{4}&{2}&{0}\\ {2}&{1}&{0}\\ {0}&{0}&{1}\end{array}}\right] Qn=E(wwT)=⎣⎡420210001⎦⎤
R n = E ( ν ν T ) = 0.7 R_{n}=E(\nu\nu^{T})=0.7 Rn=E(ννT)=0.7
对于调节器,使用以下成本函数来定义调节性能和控制输入之间的权衡:
J ( u ) = ∫ 0 ∞ ( 0.1 x T x + u T [ 1 0 0 2 ] u ) d t J(u)=\int_{0}^{\infty}(0.1x^{T}x+u^{T}\begin{bmatrix} 1&0 \\ 0&2 \end{bmatrix}u)d t J(u)=∫0∞(0.1xTx+uT[1002]u)dt
对于伺服控制器,使用以下成本函数来定义跟踪器性能和控制力之间的权衡:
J ( u ) = ∫ 0 ∞ ( 0.1 x T x + x i 2 + u T [ 1 0 0 2 ] u ) d t J(u)=\int_{0}^{\infty}(0.1x^{T}x+x_{i}^{2}+u^{T}\begin{bmatrix} 1&0 \\ 0&2 \end{bmatrix}u)d t J(u)=∫0∞(0.1xTx+xi2+uT[1002]u)dt
为该系统设计 LQG 控制器:
- 在 MATLAB 命令窗口中输入以下内容,创建状态空间系统:
A = [0 1 0;0 0 1;1 0 0];
B = [0.3 1;0 1;-0.3 0.9];
C = [1.9 1.3 1];
D = [0.53 -0.61];
sys = ss(A,B,C,D);
- 输入以下命令,定义噪声协方差数据和加权矩阵:
nx = 3; %Number of states
ny = 1; %Number of outputs
Qn = [4 2 0; 2 1 0; 0 0 1];
Rn = 0.7;
R = [1 0;0 2]
QXU = blkdiag(0.1*eye(nx),R);
QWV = blkdiag(Qn,Rn);
QI = eye(ny);
- 键入以下命令,组建 LQG 调节器:
KLQG = lqg(sys,QXU,QWV)
This command returns the following LQG regulator:
A = x1_e x2_e x3_ex1_e -6.212 -3.814 -4.136x2_e -4.038 -3.196 -1.791x3_e -1.418 -1.973 -1.766B = y1x1_e 2.365x2_e 1.432x3_e 0.7684C = x1_e x2_e x3_eu1 -0.02904 0.0008272 0.0303u2 -0.7147 -0.7115 -0.7132D = y1u1 0u2 0Input groups: Name ChannelsMeasurement 1 Output groups: Name Channels Controls 1,2 Continuous-time model.
- 键入以下命令,形成单自由度 LQG 伺服控制器:
KLQG1 = lqg(sys,QXU,QWV,QI,'1dof')
This command returns the following LQG servo controller:
A = x1_e x2_e x3_e xi1x1_e -7.626 -5.068 -4.891 0.9018x2_e -5.108 -4.146 -2.362 0.6762x3_e -2.121 -2.604 -2.141 0.4088xi1 0 0 0 0B = e1x1_e -2.365x2_e -1.432x3_e -0.7684xi1 1C = x1_e x2_e x3_e xi1u1 -0.5388 -0.4173 -0.2481 0.5578u2 -1.492 -1.388 -1.131 0.5869D = e1u1 0u2 0Input groups: Name Channels Error 1 Output groups: Name ChannelsControls 1,2 Continuous-time model.
- 输入以下命令,生成二自由度 LQG 伺服控制器:
KLQG2 = lqg(sys,QXU,QWV,QI,'2dof')
This command returns the following LQG servo controller:
A = x1_e x2_e x3_e xi1x1_e -7.626 -5.068 -4.891 0.9018x2_e -5.108 -4.146 -2.362 0.6762x3_e -2.121 -2.604 -2.141 0.4088xi1 0 0 0 0B = r1 y1x1_e 0 2.365x2_e 0 1.432x3_e 0 0.7684xi1 1 -1C = x1_e x2_e x3_e xi1u1 -0.5388 -0.4173 -0.2481 0.5578u2 -1.492 -1.388 -1.131 0.5869D = r1 y1u1 0 0u2 0 0Input groups: Name ChannelsSetpoint 1 Measurement 2 Output groups: Name Channels Controls 1,2 Continuous-time model.
小贴士
lqg可用于连续时间和离散时间被控对象。在离散时间情况下,lqg默认使用x[n|n-1]作为状态估计值。要使用x[n|n]作为状态估计并计算最优 LQG 控制器,请使用 "current"输入参数。有关状态估计器的详细信息,请参见
kalman。计算
LQG调节器时,lqg 使用 lqr 和kalman命令。要计算伺服控制器,lqg使用lqi和kalman命令。如果希望更灵活地设计调节器,可以使用
lqr、kalman和lqgreg命令。在设计伺服控制器时,如果需要更大的灵活性,可以使用lqi、kalman和lqgtrack
命令。有关使用这些命令以及如何决定何时使用这些命令的更多信息,请参阅线性-二次方-高斯 (LQG)
调节设计和带积分动作的伺服控制器的线性-二次方-高斯 (LQG) 设计。
LQG 算法
控制器方程为
- 对于连续时间: d x e = A x e + B u + L ( y − C x e − D u ) u = − K x e − K i x i d x_e=A x_e+B u+L(y-C x_e-D u) \\ u=-K x_e-K_i x_i dxe=Axe+Bu+L(y−Cxe−Du)u=−Kxe−Kixi
- 对于离散时间: x [ n + 1 ∣ n ] = A x [ n ∣ n − 1 ] + B u [ n ] + L ( y [ n ] − C x [ n ] n − 1 ] − D u [ n ] ) x[n+1|n]=A x[n|n-1]+B u[n]+L(y[n]-C x[n]n-1]-D u[n]) x[n+1∣n]=Ax[n∣n−1]+Bu[n]+L(y[n]−Cx[n]n−1]−Du[n])
- 延迟估计器: u [ n ] = − K x x [ n ] n − 1 ] − K i x i [ n ] u[n]=-K_{x}x[n]n-1]-K_{i}x_{i}[n] u[n]=−Kxx[n]n−1]−Kixi[n]
- 目前的估算器: u [ n ] = − K x x [ n ] n ] − K i x i [ n ] − K w w [ n ] = − K x x [ n ] n − 1 ] − K i x i [ n ] − ( K x M x + K w M w ) y i n n [ n ] {u[n]=-K_{x}x[n]n]-K_{i}x_{i}[n]-K_{w}w[n]=-K_{x}x[n]n-1]-K_{i}x_{i}[n]-(K_{x}M_{x}+K_{w}M_{w})y_{ i n n}[n]} u[n]=−Kxx[n]n]−Kixi[n]−Kww[n]=−Kxx[n]n−1]−Kixi[n]−(KxMx+KwMw)yinn[n] y i n n [ n ] = y [ n ] − C x [ n ] n − 1 ] − D u [ n ] y_{i n n}[n]=y[n]-C x[n]n-1]-D u[n] yinn[n]=y[n]−Cx[n]n−1]−Du[n]
这里
A、B、C 和 D 是 LQG 调节器的状态空间矩阵,reg.
x i x_i xi 是跟踪误差 r - y 的积分。
K x K_x Kx、 K w K_w Kw、 K i K_i Ki、L、 M x M_x Mx 和 M w M_w Mw 是信息中返回的控制器和估计器增益矩阵。
1.3 极点配置 —— place() 函数
1.3.1 函数用法
K = place(A,B,p)
[K,prec] = place(A,B,p)
说明
极点配置是一种计算最优增益矩阵的方法,用于将闭环极点分配给指定位置,从而确保系统稳定性。闭环极点位置会直接影响上升时间、稳定时间和瞬变振荡等时间响应特性。有关详细信息,请参阅极点配置。
从图中,假设有以下状态空间形式的线性动态系统:
x ˙ = A x + B u y = C x + D u \begin{array}{c}{{\dot{x}=A x+B u}}\\ {{}}\\ {{y=C x+D u}}\end{array} x˙=Ax+Buy=Cx+Du
对于期望的自共轭闭环极点位置的给定向量p,place计算增益矩阵K,使得状态反馈u = –Kx将极点配置在位置p。换句话说,A - BK的特征值将匹配p的条目(取决于排序)。
K = place(A,B,p)通过计算状态反馈增益矩阵K,配置所需的闭环极点p。被控对象的所有输入都假定为控制输入。
place也适用于多输入系统,并且基于 [1] 中的算法。此算法使用额外的自由度来求一个解,以使闭环极点对于A或B中的扰动具有最小的敏感度。
[K,prec] = place(A,B,p)还返回prec,用于精确估计A - BK的特征值与指定位置p的匹配程度(prec可计算实际闭环极点中的精确小数位数)。如果某个非零闭环极点偏离期望位置超出10%,则系统会发出警告。
输入参数
A — 状态矩阵 状态矩阵,指定为一个 Nx×Nx 矩阵,其中 Nx 是状态数。
B — 输入-状态矩阵 输入-状态矩阵,指定为 Nx×Nu 矩阵,其中 Nx 是状态数,Nu 是输入数。
p — 闭环极点位置 闭环极点位置,指定为长度为 Nx 的向量,其中 Nx 是状态数。换句话说,p 的长度必须与 A 的行大小匹配。闭环极点位置会直接影响上升时间、稳定时间和瞬变振荡等时间响应特性。有关选择极点的示例,请参阅二阶系统的极点配置设计。
如果 p 中某些极点的重数大于 rank(B),则 place 返回错误。
在高阶问题中,选择某些极点位置会导致增益非常大。大增益会带来敏感性问题,这表明在使用极点配置方法时要小心。有关数值测试的结果,请参阅 [2]。
输出参数
K — 最优增益 最优增益或全状态反馈增益,以 Ny×Nx 矩阵形式返回,其中 Nx 是状态数,Ny 是输出数。place 计算增益矩阵
K,使得状态反馈 u = -Kx 将闭环极点配置于位置 p。当矩阵 A 和 B 为实数时,则 K 为:
实数,前提是 p 具有自共轭性。
复数,前提是极点位置不具有复共轭性。
prec — 指定极点的准确性估计值 指定极点的准确性估计值,以标量形式返回。prec 对比 p
中指定的极点位置来计算实际闭环极点的精确小数位数。
1.3.2 示例
1.3.2.1 二阶系统的极点配置设计
对于此示例,假设有一个具有以下状态空间矩阵的简单二阶系统:
A = [ − 1 − 2 1 0 ] B = [ 2 0 ] C = [ 0 1 ] D = 0 A={\left[\begin{array}{l l}{-1}&{-2}\\ {1}&{0}\end{array}\right]}\quad B={\left[\begin{array}{l l}2\\ {0}\end{array}\right]}\quad C=\left[0\quad1\right]\quad D=0 A=[−11−20]B=[20]C=[01]D=0
输入矩阵并创建状态空间系统。
A = [-1,-2;1,0];
B = [2;0];
C = [0,1];
D = 0;
sys = ss(A,B,C,D);
计算开环极点并检查开环系统的阶跃响应。
Pol = pole(sys)
Pol = 2×1 complex-0.5000 + 1.3229i-0.5000 - 1.3229i
figure(1)
step(sys)
hold on;

请注意,生成的系统为欠阻尼系统。因此,选择复平面左半部分的实极点来消除振荡。
p = [-1,-2];
使用极点配置求增益矩阵 K,并检查 syscl 的闭环极点。
K = place(A,B,p);
Acl = A-B*K;
syscl = ss(Acl,B,C,D);
Pcl = pole(syscl)
Pcl = 2×1-2.0000-1.0000
现在,比较闭环系统的阶跃响应。
figure(1)
step(syscl)

因此,使用极点配置获得的闭环系统是稳定的,具有良好的稳态响应。
请注意,选择远离虚轴的极点可以缩短响应时间,但会减小系统的稳态增益。例如,假设上述系统使用极点 [-2,-3]。
p = [-2, -3];
K2 = place(A,B,p);
syscl2 = ss(A-B*K2,B,C,D);
figure(1);
step(syscl2);

stepinfo(syscl)
ans = struct with fields:RiseTime: 2.5901TransientTime: 4.6002SettlingTime: 4.6002SettlingMin: 0.9023SettlingMax: 0.9992Overshoot: 0Undershoot: 0Peak: 0.9992PeakTime: 7.7827
stepinfo(syscl2)
ans = struct with fields:RiseTime: 1.4130TransientTime: 2.4766SettlingTime: 2.4766SettlingMin: 0.3003SettlingMax: 0.3331Overshoot: 0Undershoot: 0Peak: 0.3331PeakTime: 4.12161.3.2.2 极点配置观测器设计
对于此示例,假设有以下 SISO 状态空间模型:
A = [ − 1 − 0.75 1 0 ] B = [ 1 0 ] C = [ 1 1 ] D = 0 A={\left[\begin{array}{l l}{-1}&{-0.75}\\ {1}&{0}\end{array}\right]}\quad B={\left[\begin{array}{l l}1\\ {0}\end{array}\right]}\quad C=\left[1\quad1\right]\quad D=0 A=[−11−0.750]B=[10]C=[11]D=0
创建由以下状态空间矩阵定义的 SISO 状态空间模型:
创建由以下状态空间矩阵定义的 SISO 状态空间模型:
现在,向被控对象提供一个脉冲,并使用 lsim 对其进行仿真。绘制输出。
N = 250;
t = linspace(0,25,N);
u = [ones(N/2,1); zeros(N/2,1)];
x0 = [1;2];
[y,t,x] = lsim(Plant,u,t,x0);figure
plot(t,y);
title('Output');

对于此示例,假设所有状态变量都无法测量,只有输出才能测量。因此,使用这种测量方法设计一个观测器。使用 place 来计算估计器增益,方法是转置 A 矩阵,并用 C’ 代换矩阵 B。对于此实例,将所需的极点位置选为 -2 和 -3。
L = place(A',C',[-2,-3])';
使用估计器增益,依据对偶/分离原理代换状态矩阵,并创建估计的状态空间模型。
At = A-L*C;
Bt = [B,L];
Ct = [C;eye(2)];
sysObserver = ss(At,Bt,Ct,0);
使用相同的脉冲输入对系统的时间响应进行仿真。
[observerOutput,t] = lsim(sysObserver,[u,y],t);
yHat = observerOutput(:,1);
xHat = observerOutput(:,[2 3]);
比较实际系统和估计系统的响应。
figure;
plot(t,x);
hold on;
plot(t,xHat,'--');
legend('x_1','x_2','xHat_1','xHat_2')
title('Comparison - Actual vs. Estimated');

相关文章:

MATLAB 状态空间设计 —— LQG/LQR 和极点配置算法
系列文章目录 文章目录 系列文章目录前言一、相关函数 —— LQG/LQR 和极点配置算法1.1 LQR —— lqr 函数1.1.1 函数用法1.1.2 举例1.1.2.1 倒摆模型的 LQR 控制 1.2 LQG —— lqg() 函数1.2.1 函数用法1.2.2 举例 1.3 极点配置 —— place() 函数1.3.1 函数用法1.3.2 示例1.3…...
杭州-区块链前瞻性论坛邀请函
2023密码与安全前瞻性论坛邀请函 生成合法节点或非法节点,测试共识协议...

ElasticSearch学习篇6_ES实践与Lucene对比及原理分析技术分享小记
前言 QBM、MFS的试题检索、试题查重、公式转换映射等业务场景以及XOP题库广泛使用搜索中间件,业务场景有着数据量大、对内容搜索性能要求高等特点,其中XOP题库数据量更是接近1亿,对检索性能以及召回率要求高。目前QBM、MFS使用的搜索中间件是…...
mysql练习1
-- 1.查询出部门编号为BM01的所有员工 SELECT* FROMemp e WHEREe.deptno BM01; -- 2.所有销售人员的姓名、编号和部门编号。 SELECTe.empname,e.empno,e.deptno FROMemp e WHEREe.empstation "销售人员";-- 3.找出奖金高于工资的员工。 SELECT* FROMemp2 WHE…...
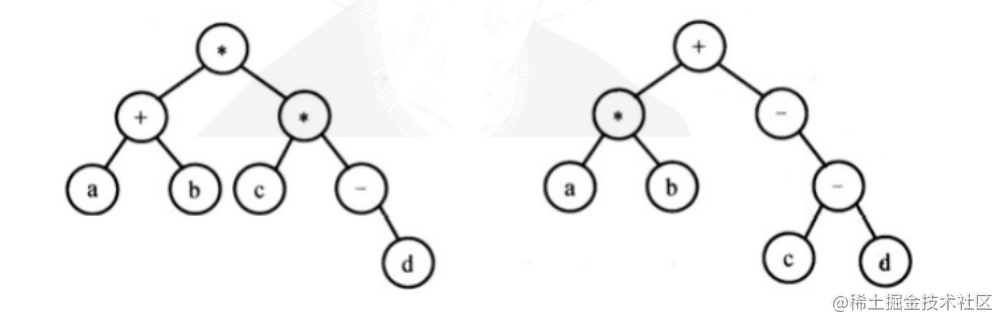
【2017年数据结构真题】
请设计一个算法,将给定的表达式树(二叉树)转换成等价的中缀表达式(通过括号反映次序),并输出。例如,当下列两棵表达式树作为算法的输入时: 输出的等价中缀表达式分别为(ab)(a(-d)) 和…...
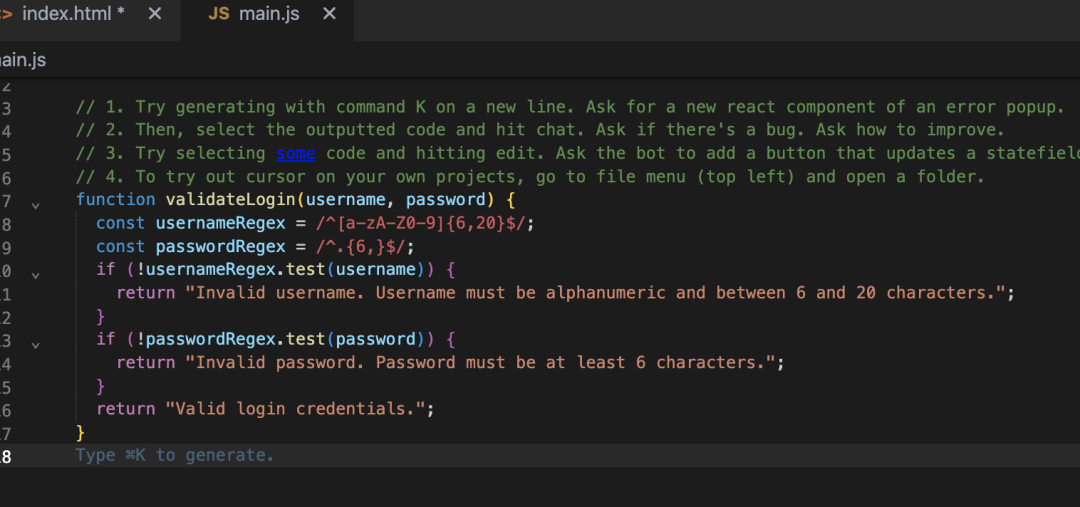
神辅助 Cursor 编辑器,加入 GPT-4 让编码更轻松!
分类 互联网 在 ChatGPT 问世之前,我们的编码方式很多时候都是面向搜索引擎编码,需要不断地进行搜索,然后复制粘贴,俗称复制粘贴工程师。 但是,随着ChatGPT的出现,这一切将彻底改变。 ChatGPT 是一种基于…...
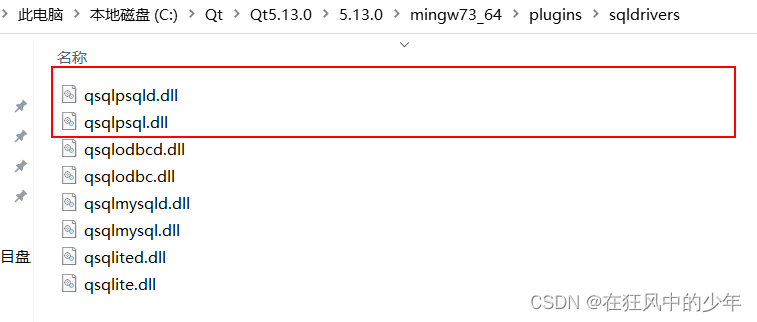
解决Qt5.13.0无MySQL驱动问题
一、前言 由于Qt5.12.3是最后提供mysql数据库插件的版本,往后的版本需要自行编译对应的mysql数据库插件,官方安装包不再提供。使用高版本的Qt就需要自行编译mysql驱动。 若没有编译在QT中调用Qsqldatabase库连接mysql时,提示出现如下问题&a…...

YOLOv8改进 | 如何在网络结构中添加注意力机制、C2f、卷积、Neck、检测头
一、本文介绍 本篇文章的内容是在大家得到一个改进版本的C2f一个新的注意力机制、或者一个新的卷积模块、或者是检测头的时候如何替换我们YOLOv8模型中的原有的模块,从而用你的模块去进行训练模型或者检测。因为最近开了一个专栏里面涉及到挺多改进的地方ÿ…...

记录一个困难
Mysql加插件 create table tb_xuesheng1 as select * from tb_xuesheng; 会报如下错误 SQL 错误 [3185] [HY000]: Cant find master key from keyring, please check in the server log if a keyring is loaded and initialized successfully.当我去搜寻答案网上都说缺少插件…...

Linux 进程管理 实时调度类及SMP和NUMA
文章目录 一、 实时调度类分析1.1 实时调度实体sched_rt_entity数据结构1.2 实时调度类rt_sched_class数据结构1.3 实时调度类功能函数 二、SMP和NUMA2.1 SMP(多对称处理器结构,UMA)2.2 NUMA(非一致内存访问结构)2.3 C…...
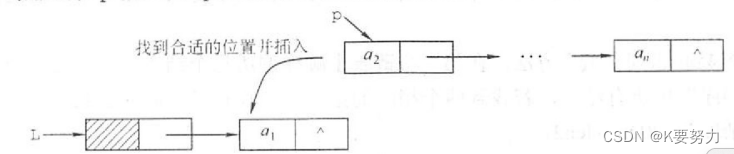
线性表--链表-1
文章目录 主要内容一.链表练习题1.设计一个递归算法,删除不带头结点的单链表 L 中所有值为 X 的结点代码如下(示例): 2.设 L为带头结点的单链表,编写算法实现从尾到头反向输出每个结点的值代码如下(示例): …...

WPF小知识
在编写WPF程序遇到一些小问题,所以记录起来,查其他方便。 Label自动换行 网上搜的都不能自动换行,发现使用Run 就可以。在脚本中直接调用labTip.Text进行赋值就可以了。 <Label Foreground"#FF9E9E9E" FontSize"16"…...

坐标系下的运动旋量转换
坐标系下的运动旋量转换 文章目录 坐标系下的运动旋量转换前言一、运动旋量物体运动旋量空间运动旋量 二、伴随变换矩阵三、坐标系下运动旋量的转换四、力旋量五、总结参考资料 前言 对于刚体而言,其角速度可以写为 ω ^ θ ˙ \hat {\omega} \dot \theta ω^θ˙&…...

Android Termux安装MySQL,通过内网穿透实现公网远程访问
🔥博客主页: 小羊失眠啦. 🔖系列专栏: C语言、Linux、Cpolar ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 前言1.安装MariaDB2.安装cpolar内网穿透工具3. 创建安全隧道映射mysql4. 公网远程连接5. 固定远程连接地址 前…...

Python in Visual Studio Code 2023年11月发布
排版:Alan Wang 我们很高兴地宣布 Visual Studio Code 的 Python 和 Jupyter 扩展将于 2023 年 11 月发布! 此版本包括以下公告: 改进了使用 Shift Enter 在终端中运行当前行弃用内置 linting 和格式设置功能对 Python linting 扩展的改进重…...
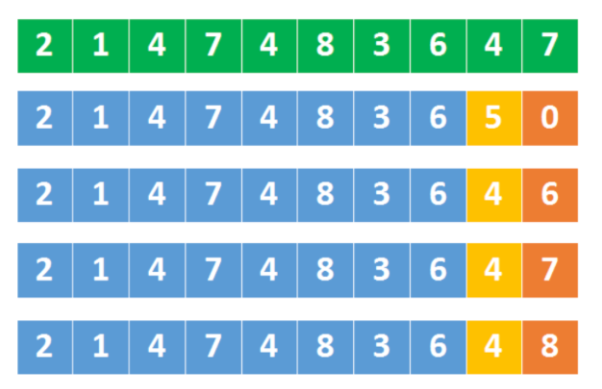
算法通关村——数字中的统计、溢出、进制转换处理模板
数字与数学基础问题 1、数字统计 1.1、符号统计 LeetCode1822. 给定一个数组,求所有元素的乘积的符号,如果最终答案是负的返回-1,如果最终答案是正的返回1,如果答案是0返回0. 这题其实只用看数组中0和负数的个数就好了&#x…...

ESP01S通过心知天气获取天气和时间信息
ESP01S通过心知天气获取天气和时间信息 设置STA模式 ATCWMODE1 连接wifi ATCWJAP"wifi名称","wifi密码"3.设置时间地域 ATCIPSNTPCFG1,8获取时间 ATCIPSNTPTIME?返回: CIPSNTPTIME:Fri Nov 17 17:09:22 2023 OK连接心知服务器 ATCIPSTAR…...

docker容器内core dumped却找不到core文件
1. 检查ulimit, 使用命令: ulimit -a rootb7c19f6da1e3:/usr# ulimit -a core file size (blocks, -c) unlimited data seg size (kbytes, -d) unlimited scheduling priority (-e) 0 file size (blocks…...
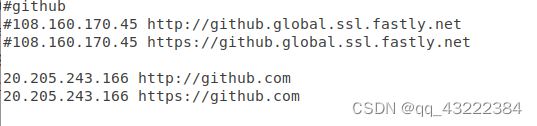
ubuntu提高 github下载速度
Github一般用于Git的远程仓库,由于服务器位于国外,国内访问速度比较慢,为了提高访问速度,决定绕过DNS域名解析。 获取Github的IP地址 按下ctrl+alt+T打开命令终端,输入: nslookup gi…...

Node.js之path路径模块
让我为大家介绍一下path路径模块吧! 什么是path路径模块? path 模块是 Node.s 官方提供的、用来处理路径的模块。它提供了一系列的方法和属性,用来满足用户对路径的处理需求。 介绍三个关于path模块的方法: path.join() 方法&…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...



