【每日一题】三个无重叠子数组的最大和
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:滑动窗口
- 写在最后
Tag
【滑动窗口】【数组】【2023-11-19】
题目来源
689. 三个无重叠子数组的最大和

题目解读
解题思路
方法一:滑动窗口
单个子数组的最大和
我们先来考虑一个长度为 k 的子数组的最大值与取得最大值时的初始位置。可以使用固定长度的滑动窗口来解决本题。
滑动窗口是数组和字符串等问题中常用的一个概念。利用滑动窗口可以去掉重复的运算,从而降低时间复杂度。滑动窗口的 “滑动” 指的是窗口每次向右移动一个位置,那么该窗口内的就会增加原窗口右侧的元素,并且会减少原窗口左端点的元素。
我们从数组 [0, k-1] 区间开始,不断地向右滑动窗口,直至窗口右端点到达数组末尾时停止。统计这一过程中长度为 k 的窗口内元素和 sum1 的最大值(记为 maxSum1)及其对应位置。
实现代码为:
class Solution {
public:vector<int> maxSumOfOneSubarray(vector<int> &nums, int k) {vector<int> ans;int sum1 = 0, maxSum1 = 0;for (int i = 0; i < nums.size(); ++i) {sum1 += nums[i];if (i >= k - 1) {if (sum1 > maxSum1) {maxSum1 = sum1;ans = {maxSum1, i - k + 1};}sum1 -= nums[i - k + 1];}}return ans;}
};
两个子数组的最大和
我们可以仿照 单个子数组的最大和 问题的解题方法,使用两个固定长度的滑动窗口来求解 两个子数组的最大和。
设 sum1 为第一个滑动窗口的元素和,该滑动窗口从 [0, k - 1] 开始,sum2 为第二个滑动窗口的元素和,该滑动窗口从 [k, 2*k - 1] 开始。我们同时向右滑动这两个窗口,并维护 sum1 的最大值 maxSum1 及其对应位置。每次滑动时,记录当前的 maxSum1 与 sum2 之和。统计这一过程中的 maxSum1 + sum2 的最大值(记作 maxSum12)及其对应位置。
实现代码为:
class Solution {
public:vector<int> maxSumOfTwoSubarrays(vector<int> &nums, int k) {vector<int> ans;int sum1 = 0, maxSum1 = 0, maxSum1Idx = 0;int sum2 = 0, maxSum12 = 0;for (int i = k; i < nums.size(); ++i) {sum1 += nums[i - k];sum2 += nums[i];if (i >= k * 2 - 1) {if (sum1 > maxSum1) {maxSum1 = sum1;maxSum1Idx = i - k * 2 + 1;}if (maxSum1 + sum2 > maxSum12) {maxSum12 = maxSum1 + sum2;ans = {maxSum1Idx, i - k + 1};}sum1 -= nums[i - k * 2 + 1];sum2 -= nums[i - k + 1];}}return ans;}
};
三个子数组的最大和
在本题中,可以使用三个长度为 k 的滑动窗口。设 sum1 为第一个滑动窗口的元素和,该滑动窗口从 [0, k - 1] 开始,sum2 为第二个滑动窗口的元素和,该滑动窗口从 [k, 2*k - 1] 开始,sum3 为第三个滑动窗口的元素和,该滑动窗口从 [2*k, 3*k - 1] 开始。
我们同时向右滑动这三个窗口,并维护 maxSum12 及其对应位置。每次滑动时,记录当前的 maxSum12 与 sum3 之和。统计这一过程中的 maxSum12 + sum3 的最大值(记作 maxTotal)及其对应位置。
对于题目要求的最小字典序,由于我们是从左向右遍历的,并且仅当元素和超过最大元素和时才修改最大元素和,从而保证求出来的下标列表是字典序最小的。
复杂度分析
class Solution {
public:vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {vector<int> res;int sum1 = 0, maxSum1 = 0, maxSum1Idx = 0;int sum2 = 0, maxSum12 = 0, maxSum12Idx1 = 0, maxSum12Idx2 = 0;int sum3 = 0, maxTotal = 0;for (int i = 2 * k; i < nums.size(); ++i) {sum1 += nums[i - 2 * k];sum2 += nums[i - k];sum3 += nums[i];if (i >= 3 * k - 1) {if (sum1 > maxSum1) {maxSum1 = sum1;maxSum1Idx = i - 3 * k + 1; }if (maxSum1 + sum2 > maxSum12) {maxSum12 = maxSum1 + sum2;maxSum12Idx1 = maxSum1Idx;maxSum12Idx2 = i - 2 * k + 1;}if (maxSum12 + sum3 > maxTotal) {maxTotal = maxSum12 + sum3;res = {maxSum12Idx1, maxSum12Idx2, i - k + 1};}sum1 -= nums[i - 3 * k + 1];sum2 -= nums[i - 2 * k + 1];sum3 -= nums[i - k + 1];}}return res;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n)。
空间复杂度: O ( 1 ) O(1) O(1)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【每日一题】三个无重叠子数组的最大和
文章目录 Tag题目来源题目解读解题思路方法一:滑动窗口 写在最后 Tag 【滑动窗口】【数组】【2023-11-19】 题目来源 689. 三个无重叠子数组的最大和 题目解读 解题思路 方法一:滑动窗口 单个子数组的最大和 我们先来考虑一个长度为 k 的子数组的最…...
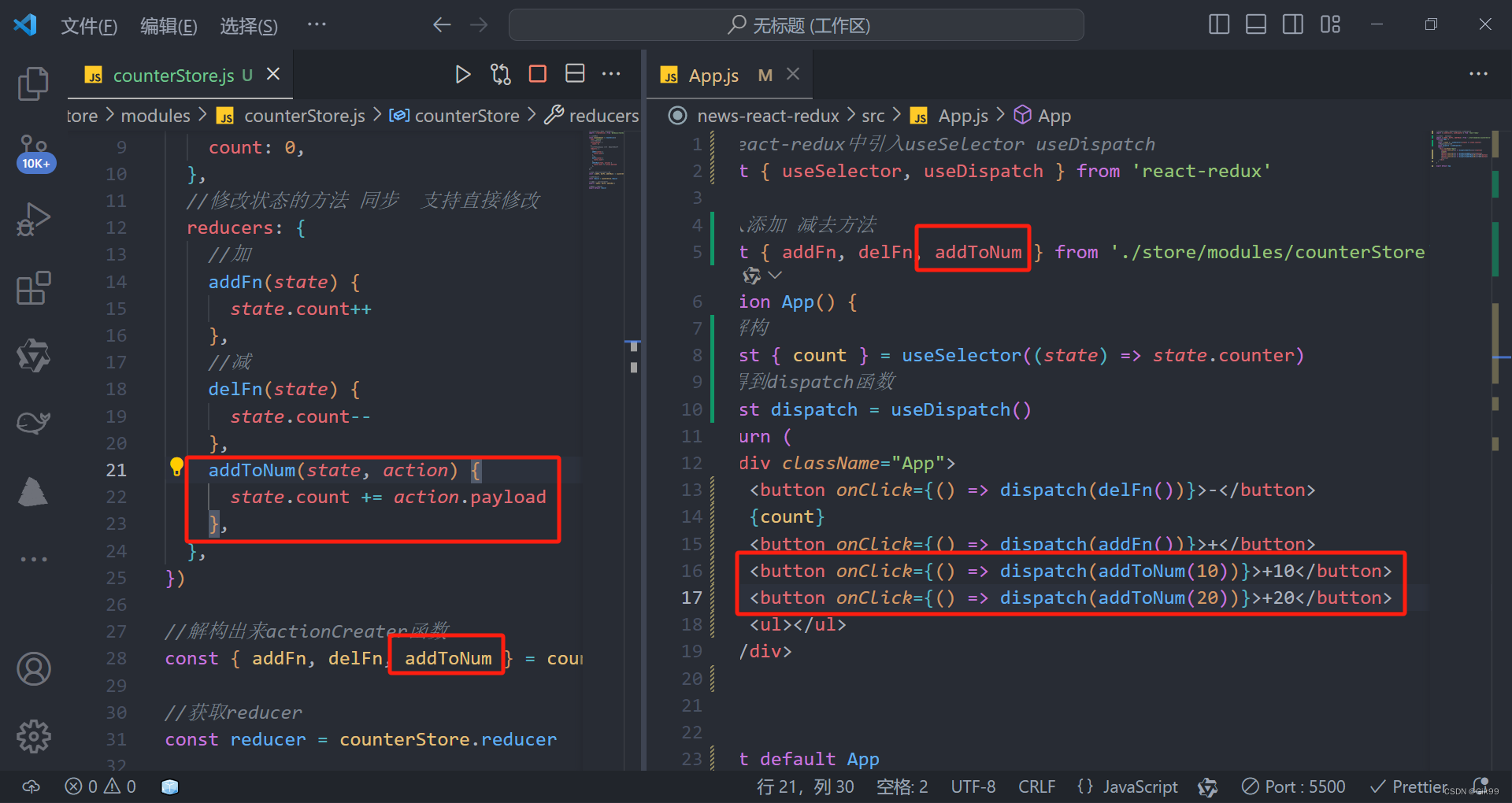
react之基于@reduxjs/toolkit使用react-redux
react之基于reduxjs/toolkit使用react-redux 一、配置基础环境二、使用React Toolkit 创建 counterStore三、为React注入store四、React组件使用store中的数据五、实现效果六、提交action传递参数七、异步状态操作 一、配置基础环境 1.使用cra快速创建一个react项目 npx crea…...
基于51单片机水位监测控制报警仿真设计( proteus仿真+程序+设计报告+讲解视频)
这里写目录标题 💥1. 主要功能:💥2. 讲解视频:💥3. 仿真💥4. 程序代码💥5. 设计报告💥6. 设计资料内容清单&&下载链接💥[资料下载链接:](https://doc…...

git基本用法和操作
文章目录 创建版本库方式:Git常用操作命令:远程仓库相关命令分支(branch)操作相关命令版本(tag)操作相关命令子模块(submodule)相关操作命令忽略一些文件、文件夹不提交其他常用命令 创建版本库方式: 创建文件夹 在目录下 右键 Git Bush H…...

设计模式-组合模式-笔记
“数据结构”模式 常常有一些组件在内部具有特定的数据结构,如果让客户程序依赖这些特定数据结构,将极大地破坏组件的复用。这时候,将这些特定数据结构封装在内部,在外部提供统一的接口,来实现与特定数据结构无关的访…...
Android 弹出自定义对话框
Android在任意Activity界面弹出一个自定义的对话框,效果如下图所示: 准备一张小图片,右上角的小X图标64*64,close_icon.png,随便找个小图片代替; 第一步:样式添加,注意:默认在value…...
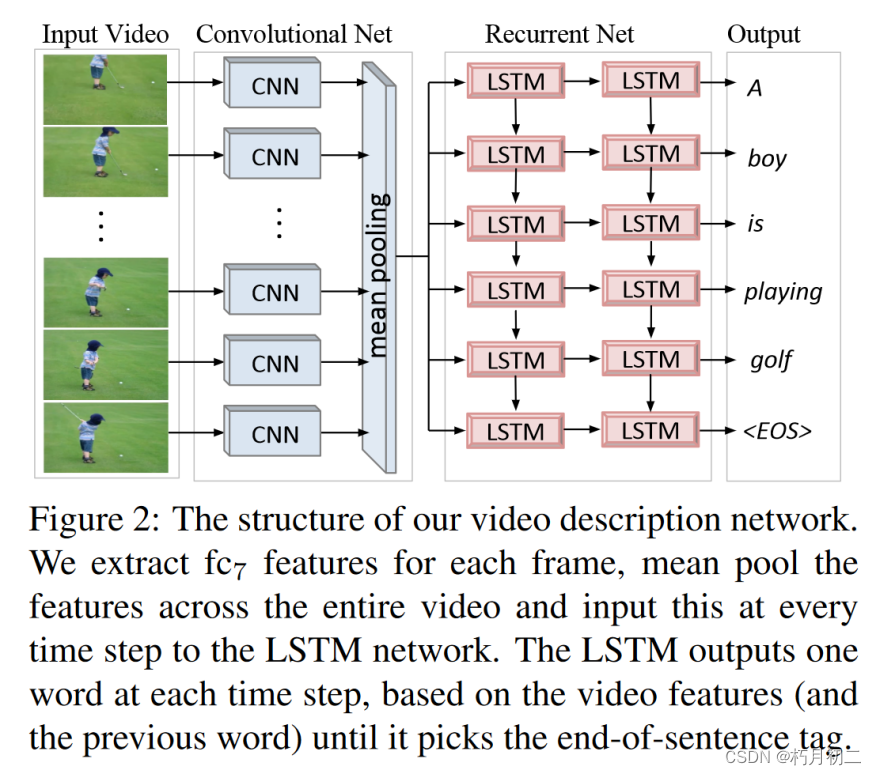
(论文阅读40-45)图像描述1
40.文献阅读笔记(m-RNN) 简介 题目 Explain Images with Multimodal Recurrent Neural Networks 作者 Junhua Mao, Wei Xu, Yi Yang, Jiang Wang, Alan L. Yuille, arXiv:1410.1090 原文链接 http://arxiv.org/pdf/1410.1090.pdf 关键词 m-RNN、…...
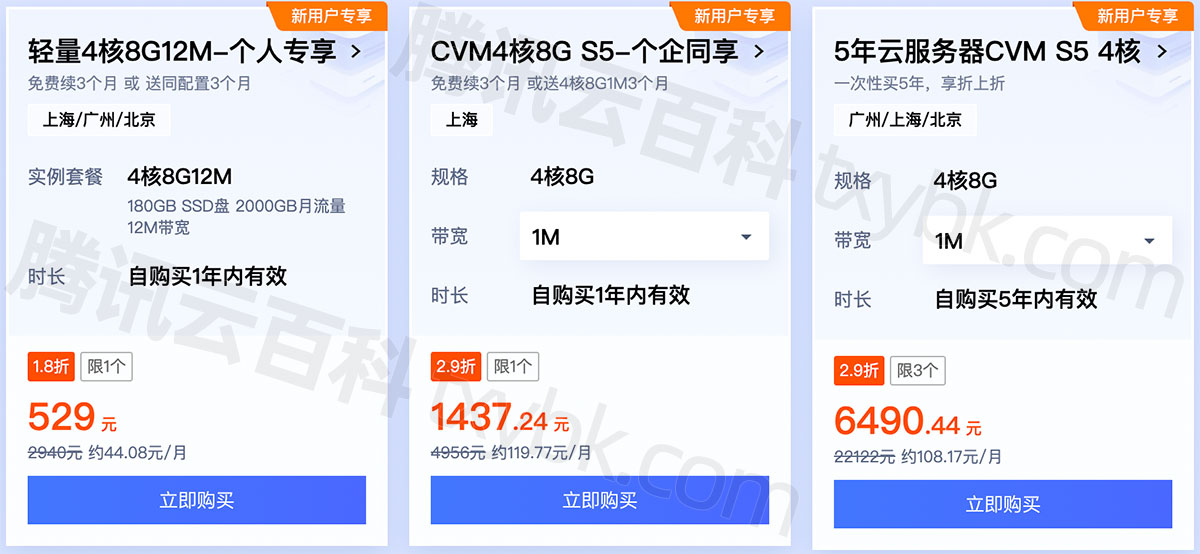
4核8G服务器价格选择轻量还是CVM合适?
腾讯云服务器4核8G配置优惠价格表,轻量应用服务器和CVM云服务器均有活动,云服务器CVM标准型S5实例4核8G配置价格15个月1437.3元,5年6490.44元,轻量应用服务器4核8G12M带宽一年446元、529元15个月,腾讯云百科txybk.com分…...

Selenium操作已经打开的Chrome浏览器窗口
Selenium操作已经打开的Chrome浏览器窗口 0. 背景 在使用之前的代码通过selenium操作Chrome浏览器时,每次都要新打开一个窗口,觉得麻烦,所以尝试使用 Selenium 获取已经打开的浏览器窗口,在此记录下过程 本文使用 chrome浏览器来…...

创新研报|新业务发展是CEO推动企业增长的必要选择 – Mckinsey研究
🔍📈 创新研究报告 |新业务拓展:CEO推动企业成长的必然选择 – 麦肯锡研究 🔥💼 所有执行长和商界领袖请注意!您是否正在寻找为您的组织释放成长机会的钥匙? 🌐 麦肯锡最近的一份研究…...

rv1126-rv1109-openssh
这是一个工具,可以通过ssh远程登录来操作,非常逆天! 于是rv1109代码自身自带有openssh 所以只需要打开config即可 diff --git a/buildroot/configs/rockchip_rv1126_rv1109_spi_nand_defconfig b/buildroot/configs/rockchip_rv1126_rv1109…...

MySQL中json类型,你使用过吗
在最近的项目开发过程中,遇到了消息发送内容以Map形式存储的情况。最初的解决方案是将对象转换为字符串,并存储在MySQL的varchar(3000)字段中。然而,由于对存储空间的限制,不得不寻找其他解决方案。在调研中发现,从MyS…...

MATLAB 状态空间设计 —— LQG/LQR 和极点配置算法
系列文章目录 文章目录 系列文章目录前言一、相关函数 —— LQG/LQR 和极点配置算法1.1 LQR —— lqr 函数1.1.1 函数用法1.1.2 举例1.1.2.1 倒摆模型的 LQR 控制 1.2 LQG —— lqg() 函数1.2.1 函数用法1.2.2 举例 1.3 极点配置 —— place() 函数1.3.1 函数用法1.3.2 示例1.3…...
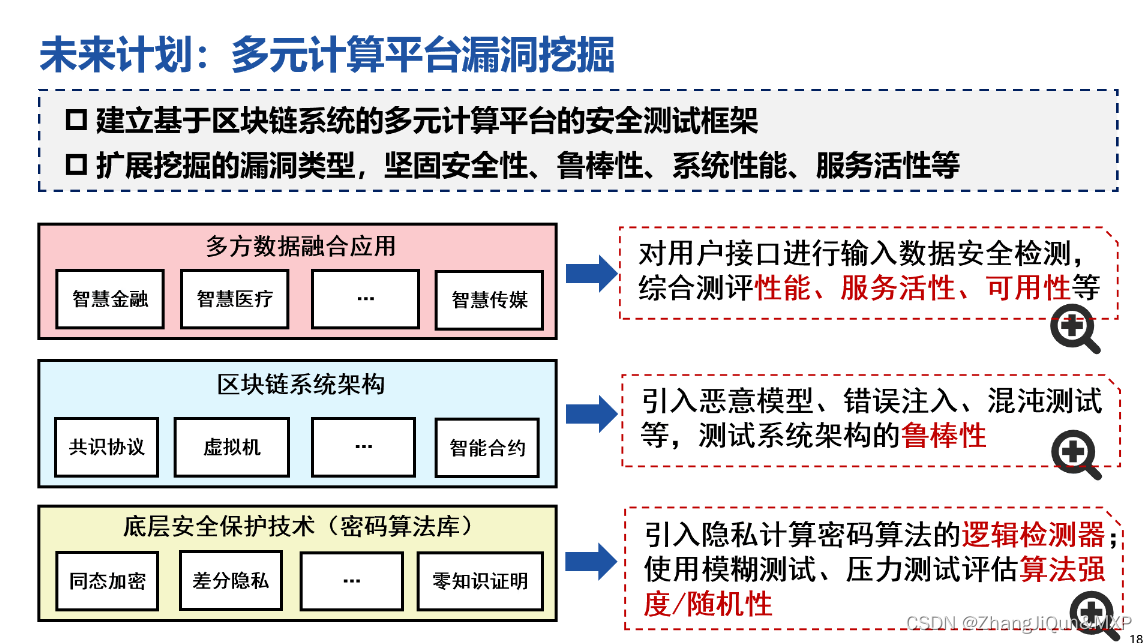
杭州-区块链前瞻性论坛邀请函
2023密码与安全前瞻性论坛邀请函 生成合法节点或非法节点,测试共识协议...

ElasticSearch学习篇6_ES实践与Lucene对比及原理分析技术分享小记
前言 QBM、MFS的试题检索、试题查重、公式转换映射等业务场景以及XOP题库广泛使用搜索中间件,业务场景有着数据量大、对内容搜索性能要求高等特点,其中XOP题库数据量更是接近1亿,对检索性能以及召回率要求高。目前QBM、MFS使用的搜索中间件是…...
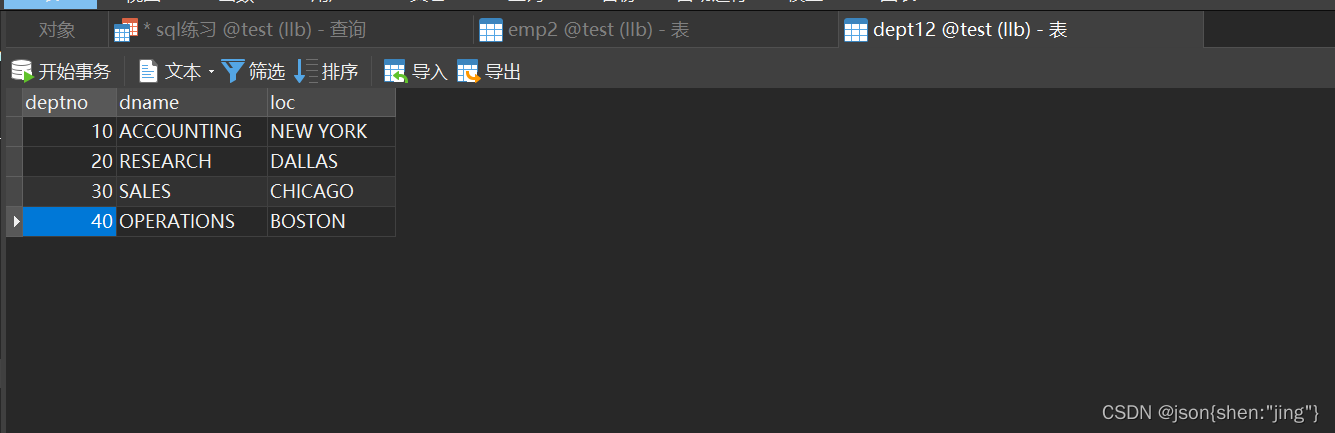
mysql练习1
-- 1.查询出部门编号为BM01的所有员工 SELECT* FROMemp e WHEREe.deptno BM01; -- 2.所有销售人员的姓名、编号和部门编号。 SELECTe.empname,e.empno,e.deptno FROMemp e WHEREe.empstation "销售人员";-- 3.找出奖金高于工资的员工。 SELECT* FROMemp2 WHE…...
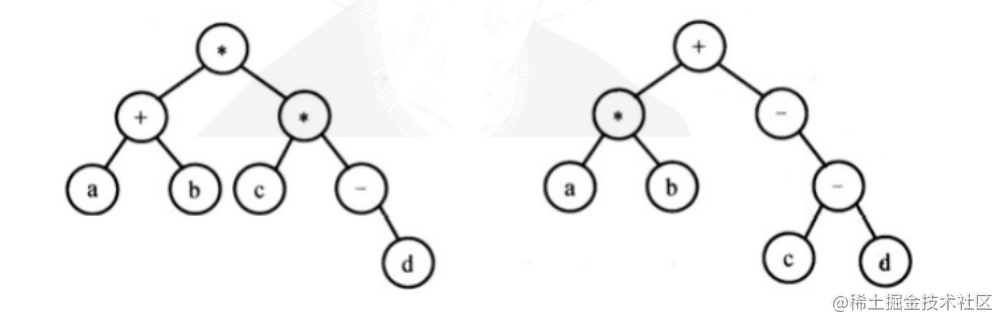
【2017年数据结构真题】
请设计一个算法,将给定的表达式树(二叉树)转换成等价的中缀表达式(通过括号反映次序),并输出。例如,当下列两棵表达式树作为算法的输入时: 输出的等价中缀表达式分别为(ab)(a(-d)) 和…...
神辅助 Cursor 编辑器,加入 GPT-4 让编码更轻松!
分类 互联网 在 ChatGPT 问世之前,我们的编码方式很多时候都是面向搜索引擎编码,需要不断地进行搜索,然后复制粘贴,俗称复制粘贴工程师。 但是,随着ChatGPT的出现,这一切将彻底改变。 ChatGPT 是一种基于…...
解决Qt5.13.0无MySQL驱动问题
一、前言 由于Qt5.12.3是最后提供mysql数据库插件的版本,往后的版本需要自行编译对应的mysql数据库插件,官方安装包不再提供。使用高版本的Qt就需要自行编译mysql驱动。 若没有编译在QT中调用Qsqldatabase库连接mysql时,提示出现如下问题&a…...

YOLOv8改进 | 如何在网络结构中添加注意力机制、C2f、卷积、Neck、检测头
一、本文介绍 本篇文章的内容是在大家得到一个改进版本的C2f一个新的注意力机制、或者一个新的卷积模块、或者是检测头的时候如何替换我们YOLOv8模型中的原有的模块,从而用你的模块去进行训练模型或者检测。因为最近开了一个专栏里面涉及到挺多改进的地方ÿ…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
