矩阵运算_矩阵的协方差矩阵/两个矩阵的协方差矩阵_求解详细步骤示例
1. 协方差矩阵定义
在统计学中,方差是用来度量单个随机变量的离散程度,而协方差则一般用来刻画两个随机变量的相似程度。
参考: 带你了解什么是Covariance Matrix协方差矩阵 - 知乎
2. 协方差矩阵计算过程
- 将输入数据A进行中心化处理得到A'。即通过减去每个维度的平均值来实现中心化。
- 注意:平均值的计算有两种方式,按行计算(如numpy)和按列计算(如matlab),两者结果是不一样的,但原理是一样的,本文采用按行计算平均值为例。
- 按列计算均值(每一行是一个observation(样本),那么每一列就是一个随机变量(特征))的一个实例:协方差矩阵计算方法_如何算瞬时协方差矩阵-CSDN博客
-
对于按行计算方式:协方差矩阵等于去中心化后的数据A'乘以A'的转置矩阵, 然后除以 (列数-1)。如果输入数据的维度为(N,M),则该乘积的形状为(N,M)和(M,N),得到一个形状为(N,N)的矩阵。即对于NxM的矩阵A, 去中心化后的矩阵为A', 则协方差等于:
-
3. 示例
一个矩阵A的协方差矩阵计算
设2x4的矩阵A为:
按行计算均值,意味着每一列是一个observation(样本),那么每一行就是一个随机变量(特征),举例如对于随机变量X,Y, 有四组采样结果(1,2), (2,3), (4,2), (1,5), 写成矩阵相乘的形式为:
则均值向量为
去中心化后的矩阵A'为:
则协方差矩阵cov(A)为:
所以,
代码numpy验算
import numpy as npA = np.array([[1, 2, 4, 1], [2, 3, 2, 5]])
print("======= cov(A) =======")
print(np.cov(A))mean_A = np.mean(A,axis=1,keepdims=True)
print("======= mean_A =======")
print(mean_A)A1 = A - mean_A
print("======= A - mean_A =======")
print(A1)covA =np.matmul(A1, A1.T)/(A1.shape[1]-1)
print("======= covA =======")
print(covA)输出结果:

两个矩阵A、B的协方差矩阵计算
设矩阵A (维度NxM), B (维度NxM),去中心化后的矩阵为A', B', 则两个矩阵的协方差矩阵cov(A,B)为:
设A,B (维度为2x4)值分别为:
,
则 按行求平均值, 得平均值向量为,
, 去中心化后,得到:
,
则其协方差矩阵 cov(A,B)(维度为4x4)为
性质:
代码numpy验算
A = np.array([[1, 2, 4, 1], [2, 3, 2, 5]])
B = np.array([[5, 3, 4, 4], [2, 2, 8, 8]])B1 = B - np.mean(B,axis=1,keepdims=True)
A1 = A - np.mean(A,axis=1,keepdims=True)C11 = np.cov(A)
C22 = np.cov(B)
C12 = np.matmul(A1, B1.T)/(B1.shape[1]-1)
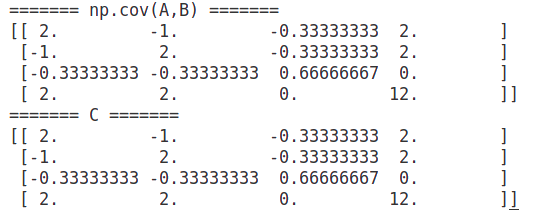
C21 = np.matmul(B1, A1.T)/(A1.shape[1]-1)C = np.vstack((np.hstack((C11,C12)),np.hstack((C21,C22))))print("======= np.cov(A,B) =======")
print(np.cov(A,B))print("======= C =======")
print(C)
结果:
参考:
协方差矩阵计算实例_协方差矩阵例子-CSDN博客
协方差的计算方法_协方差计算-CSDN博客 (matlab计算)
带你了解什么是Covariance Matrix协方差矩阵
https://wenku.csdn.net/answer/2408abac75f64f0186adff81be057f99
相关文章:

矩阵运算_矩阵的协方差矩阵/两个矩阵的协方差矩阵_求解详细步骤示例
1. 协方差矩阵定义 在统计学中,方差是用来度量单个随机变量的离散程度,而协方差则一般用来刻画两个随机变量的相似程度。 参考: 带你了解什么是Covariance Matrix协方差矩阵 - 知乎 2. 协方差矩阵计算过程 将输入数据A进行中心化处理得到A…...
——第108天:Pyecharts绘制多种炫酷词云图参数说明+代码实战)
100天精通Python(可视化篇)——第108天:Pyecharts绘制多种炫酷词云图参数说明+代码实战
文章目录 专栏导读一、词云图介绍1. 词云图是什么?2. 词云图应用场景?二、参数说明1. 导包2. add函数三、词云库实战1. 基础词云图2. 矩形词云图3. 三角形词云图4. 菱形词云图5. 自定义图片词云图书籍推荐专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本…...
Spark 平障录
Profile Profile 是最重要的第一环。 利用好 spark UI 和 yarn container log分析业务代码,对其计算代价进行预判建设基准,进行对比,比如application id 进行对比,精确到 job DAG 环节 充分利用 UI Stage 页面 页头 summary&…...

基于一致性算法的微电网分布式控制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 本模型主要是基于一致性理论的自适应虚拟阻抗、二次电压补偿以及二次频率补偿,实现功率均分,保证电压以及频率稳定性。 一致性算法 分布式一致性控制主要分为两类:协调同…...

Android 10.0 系统修改usb连接电脑mtp和PTP的显示名称
1.前言 在10.0的产品定制化开发中,在usb模块otg连接电脑,调整为mtp文件传输模式的时候,这时可以在电脑看到手机的内部存储 显示在电脑的盘符中,会有一个mtp名称做盘符,所以为了统一这个名称,就需要修改这个名称,接下来分析下处理的 方法来解决这个问题 2.系统修改usb连…...
飞鼠异地组网工具实战之访问k8s集群内部服务
飞鼠异地组网工具实战之访问k8s集群内部服务 一、飞鼠异地组网工具介绍1.1 飞鼠工具简介1.2 飞鼠工具官网 二、本次实践介绍2.1 本次实践场景描述2.2 本次实践前提2.3 本次实践环境规划 三、检查本地k8s集群环境3.1 检查k8s各节点状态3.2 检查k8s版本3.3 检查k8s系统pod状态 四…...
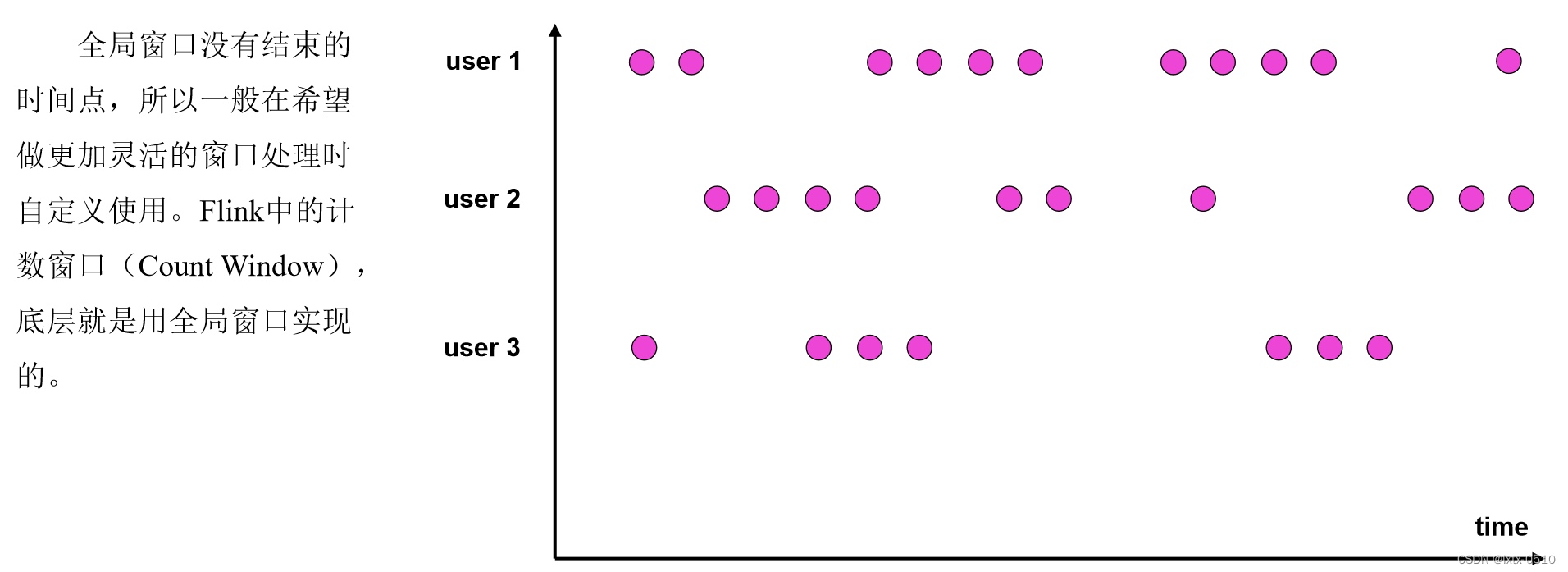
【Flink】窗口(Window)
窗口理解 窗口(Window)是处理无界流的关键所在。窗口可以将数据流装入大小有限的“桶”中,再对每个“桶”加以处理。 本文的重心将放在 Flink 如何进行窗口操作以及开发者如何尽可能地利用 Flink 所提供的功能。 对窗口的正确理解ÿ…...
读像火箭科学家一样思考笔记03_第一性原理(上)
1. 思维的两种障碍 1.1. 为什么知识会成为一种缺陷而非一种美德 1.1.1. 知识是一种美德 1.1.2. 知识同样的特质也会把它变成一种缺点 1.1.3. 知识确实是个好东西,但知识的作用应该是给人们提供信息,而不是起约束作用 1.1.4. 知识应该启发智慧&#…...

npm私有云
安装node时npm会自动安装,npm也可以单独安装。 package.json 在使用npm时,package.json文件是非常重要的,因为它包含了关于项目的必要信息,比如名称、版本、依赖项等。在初始化新项目时,通常会使用npm init命令生成一…...

莹莹API管理系统源码附带两套模板
这是一个API后台管理系统的源码,可以自定义添加接口,并自带两个模板。 环境要求 PHP版本要求高于5.6且低于8.0,已测试通过的版本为7.4。 需要安装PHPSG11加密扩展。 已测试:宝塔/主机亲测成功搭建! 安装说明 &am…...

【Kingbase FlySync】命令模式:安装部署同步软件,实现KES到KES实现同步
【Kingbase FlySync】命令模式:安装部署同步软件,实现KES到KES实现同步迁移 概述准备环境目标资源1.测试虚拟机下载地址包含node1,node22.同步工具下载地址3.临时授权下载地址4.ruby工具下载地址5.EXAMv0.11.sql下载地址 实操:同步软件安装部署1.node1准…...
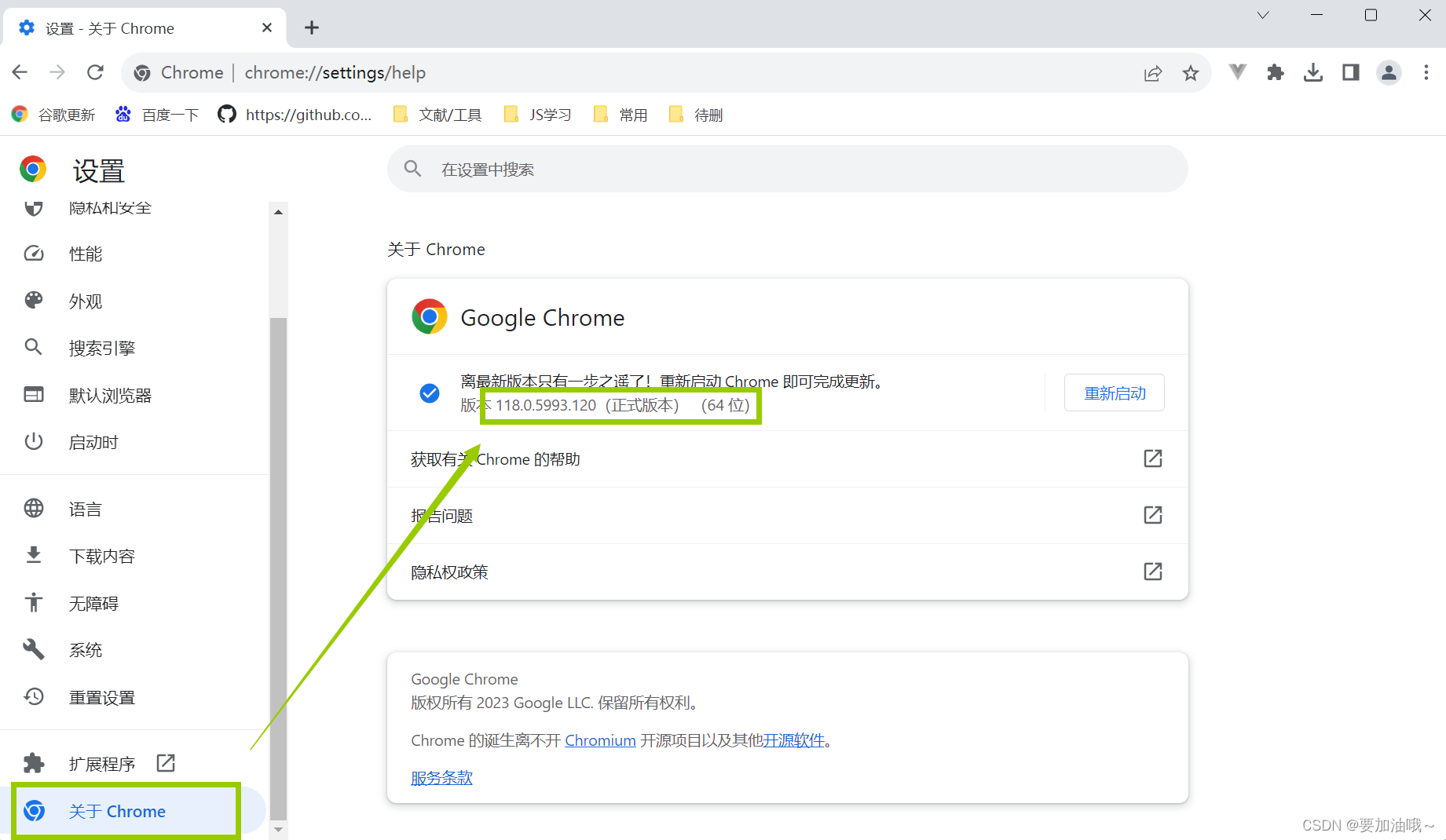
python使用selenium webDriver时 报错
可能原因和解决: 1. python 解释器 ----> 设置 2. 浏览器版本 与 浏览器驱动版本不一致 ----> 安装同一版本的 (下载chromedriver | 谷歌驱动更高版本的测试版) 参考:Python使用Selenium WebDriver的入门介绍及安装教程-CSDN博客 Selenium安…...

【ROS2机器人入门到实战】
ROS2机器人入门到实战教程(鱼香ROS) 写在前面 当前平台文章汇总地址:ROS2机器人从入门到实战获取完整教程及配套资料代码,请关注公众号<鱼香ROS>获取教程配套机器人开发平台:两驱版| 四驱版为方便交流,搭建了机器人技术问…...

Nuxt3框架局部文件引用外部JS/CSS文件的相关配置方法
引入外部JS: <script setup>useHead({script: [ {type: "text/javascript",src: https://cdnjs.cloudflare.com/ajax/libs/jquery/3.7.0/jquery.min.js}]}) </script>useHead只能与组件的setup和生命周期钩子一起使用 如果需要将js放置body区…...
Docker 可视化面板 ——Portainer
Portainer 是一个非常好用的 Docker 可视化面板,可以让你轻松地管理你的 Docker 容器。 官网:Portainer: Container Management Software for Kubernetes and Docker 【Docker系列】超级好用的Docker可视化工具——Portainer_哔哩哔哩_bilibili 环境 …...

Java 教育局民办教育信息服务与监管平台
1) 项目背景 按照《中华人民共和国民办教育促进法》和《中华人民共和国政府信息公开条例》的相关规定,为满足学生和家长、社会各界获取权威信息的需求,着力解决服务老百姓最后一公里问题,达到宣传民办教育和引导家长择校的效果࿰…...
小迪笔记(1)——操作系统文件下载反弹SHELL防火墙绕过
名词解释 POC:验证漏洞存在的代码; EXP:利用漏洞的代码; payload:漏洞利用载荷, shellcode:漏洞代码, webshell:特指网站后门; 木马:强调控制…...

Pytorch D2L Subplots方法对画图、图片处理
问题代码 def show_images(imgs, num_rows, num_cols, titlesNone, scale1.5): #save """绘制图像列表""" figsize (num_cols * scale, num_rows * scale) _, axes d2l.plt.subplots(num_rows, num_cols, figsizefigsize) axes axes.flatten…...
)
MATLAB算法实战应用案例精讲-【目标检测】YOLOV5(补充篇)
目录 算法原理 YOLOv5数据集训练 软硬件背景: 数据集准备 配置文件 模型训练...

WPF中可视化树和逻辑树的区别是什么
在WPF中,用户界面元素被组织成树形结构。这种结构主要分为两种:逻辑树(Logical Tree)和可视化树(Visual Tree)。它们在设计上各有特点和用途。 逻辑树(Logical Tree) 逻辑树是WPF中…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
