计算机网络——物理层-信道的极限容量(奈奎斯特公式、香农公式)
目录
介绍
奈氏准则
香农公式
介绍
信号在传输过程中,会受到各种因素的影响。
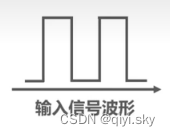
如图所示,这是一个数字信号。
当它通过实际的信道后,波形会产生失真;当失真不严重时,在输出端还可根据已失真的波形还原出发送的码元。
但当失真严重时,在输出端就很难判断这个信号在什么时候是1,和在什么时候是0。
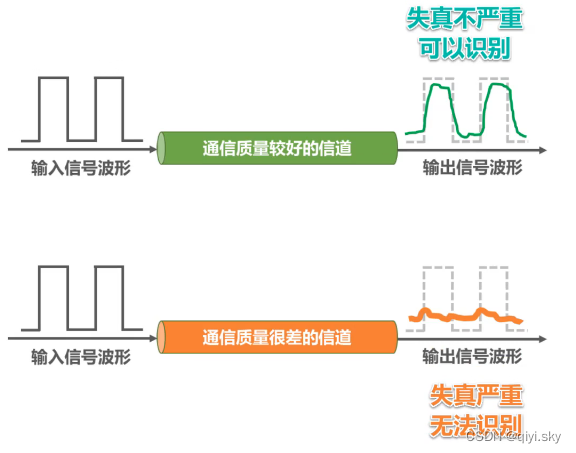
信号波形失去了码元之间的清晰界限,这种现象叫做码间串扰。
产生失真的原因主要有:
- 码元传输速率
- 信号传输距离
- 噪声干扰
- 传输媒体质量等
奈氏准则
(奈奎斯特公式)
早在1924年,奈奎斯特就推导出了著名的奈氏准则,他给出了在假定的理想条件下,为了避免码间串扰,码元传输速率的上限。
- 理想低通信道的最高码元传输速率 = 2W Baud = 2W 码元 / 秒
- 理想带通信道的最高码元传输速率 = W Baud = W 码元 / 秒
W:信道带宽(单位为 Hz)
Baud: 波特 ,即 码元 / 秒
码元传输速率又称为波特率、调制速率、波形速率或符号速率。它与比特率有一定的关系:
- 当一个码元只携带1比特的信息量时,则波特率(码元 / 秒)与比特率(比特 / 秒)在数值上是相等的;
- 当一个码元携带n比特的信息量时,则波特率转换成比特率时,数值要乘以n。
要提高信息的传输速率(比特率),就必须设法使每一个码元能够携带更多个比特的信息量。这需要采用多元制。
还记得我们之前介绍的调幅、调频以及调相这三种基本调制方法吗?
它们属于二元调制,只能产生两种不同的码元,也就是两种不同的基本波形。因此,每个码元只能携带1比特的信息量。
而混合调制属于多元调制,例如QAM16可以调制出16种不同的码元,因此,每个码元可以携带4比特的信息量。
需要说明的是:
实际的信道所能传输的最高码元速率要明显低于奈氏准则给出的这个上限值。
这是因为,奈氏准则是在假定的理想条件下推导出来的,他不考虑其他因素,例如传输距离、噪声干扰、传输媒体质量等。
仅从公式来看,只要采用更好的调制方法,让码元可以携带更多的比特,岂不是可以无限制的提高信息的传输速率吗?
答案是否定的。信道的极限信息传输速率,还要受限于实际的信号在信道中传输时的信噪比。
因为信道中的噪声也会影响接收端对码元的识别,并且噪声功率相对信号功率越大,影响就越大。
香农公式
1948年,香农用信息论的理论,推导出了带宽受限,且有高斯白噪声干扰的信道的极限信息传输速率。
具体公式如下所示:
其中c是信道的极限信息传输速率,单位是比特每秒;W是信道带宽,单位为赫兹;S是信道内所传送信号的平均功率;N是信道内的高斯噪声功率;S/N是信噪比,使用分贝作为度量单位。
信噪比(db) =
如下所示,从相同公式可以看出:信道带宽或信道中信道比越大,信息的极限传输速率就越大。

需要说明的是:
在实际信道上,能够达到的信息传输速率,要比该公式的极限传输速率低不少。
这是因为在实际信道中,信号还要受到其他一些损伤,例如各种脉冲干扰 。信号在传输中的衰减和失真等这些因素在香农公式中并未考虑。

综合来看,奈氏准则和香农公式在信道带宽一定的情况下,要想提高信息的传输速率,就必须采用多元制(更好的调制方法)和努力提高信道中的信噪比。
- 自从香农公式发表以后,各种新的信号处理和调制方法就不断出现,其目的都是为了尽可能地接近香农公式所给出的传输速率极限。
END
学习自:湖科大——计算机网络微课堂
相关文章:

计算机网络——物理层-信道的极限容量(奈奎斯特公式、香农公式)
目录 介绍 奈氏准则 香农公式 介绍 信号在传输过程中,会受到各种因素的影响。 如图所示,这是一个数字信号。 当它通过实际的信道后,波形会产生失真;当失真不严重时,在输出端还可根据已失真的波形还原出发送的码元…...

【算法挨揍日记】day31——673. 最长递增子序列的个数、646. 最长数对链
673. 最长递增子序列的个数 673. 最长递增子序列的个数 题目解析: 给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。 注意 这个数列必须是 严格 递增的。 解题思路: 算法思路: 1. 状态表⽰: 先尝试…...
Jmeter做接口测试
1.Jmeter的安装以及环境变量的配置 Jmeter是基于java语法开发的接口测试以及性能测试的工具。 jdk:17 (最新的Jeknins,只能支持到17) jmeter:5.6 官网:http://jmeter.apache.org/download_jmeter.cgi 认识JMeter的目录࿱…...

第14届蓝桥杯青少组python试题解析:23年5月省赛
选择题 T1. 执行以下代码,输出结果是()。 lst "abc" print(lstlst)abcabc abc lstlst abcabc T2. 执行以下代码,输出的结果是()。 age {16,18,17} print(type(sorted(age)))<class set&…...
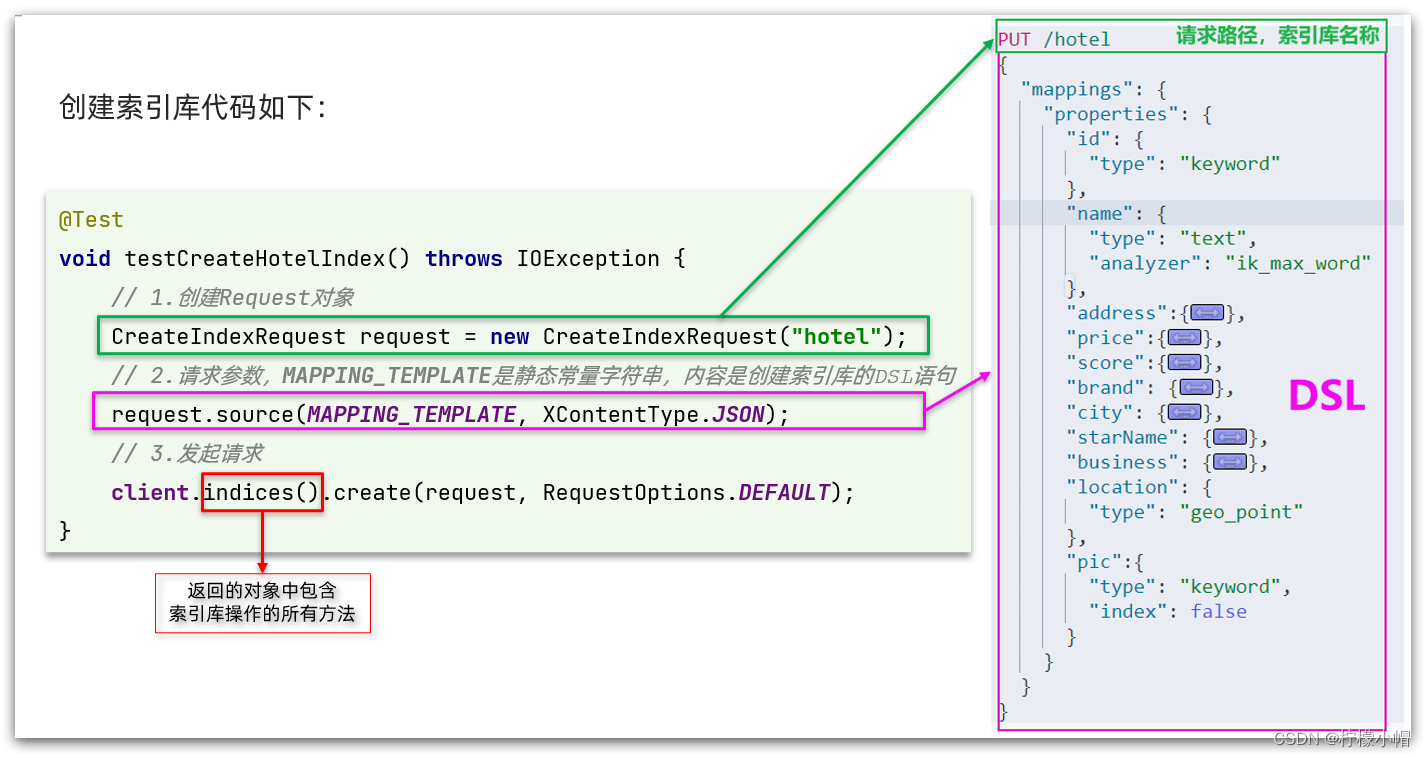
SpringCloud 微服务全栈体系(十四)
第十一章 分布式搜索引擎 elasticsearch 四、RestAPI ES 官方提供了各种不同语言的客户端,用来操作 ES。这些客户端的本质就是组装 DSL 语句,通过 http 请求发送给 ES。官方文档地址:https://www.elastic.co/guide/en/elasticsearch/client/…...

【开题报告】基于微信小程序的个人健康管理系统的设计与实现
1.选题背景与意义 在现代社会,人们对健康的关注日益增加。随着生活方式的变化和工作压力的增加,许多人意识到保持良好的身体健康对于提高生活质量和幸福感的重要性。 然而,许多人在日常生活中缺乏对自身健康状况的了解和管理。他们可能没有…...

Swagger笔记
一、导包 <!--引入swagger--> <dependency><groupId>io.springfox</groupId><artifactId>springfox-swagger2</artifactId><version>2.9.2</version> </dependency> <!--前端的UI界面--> <dependency><…...
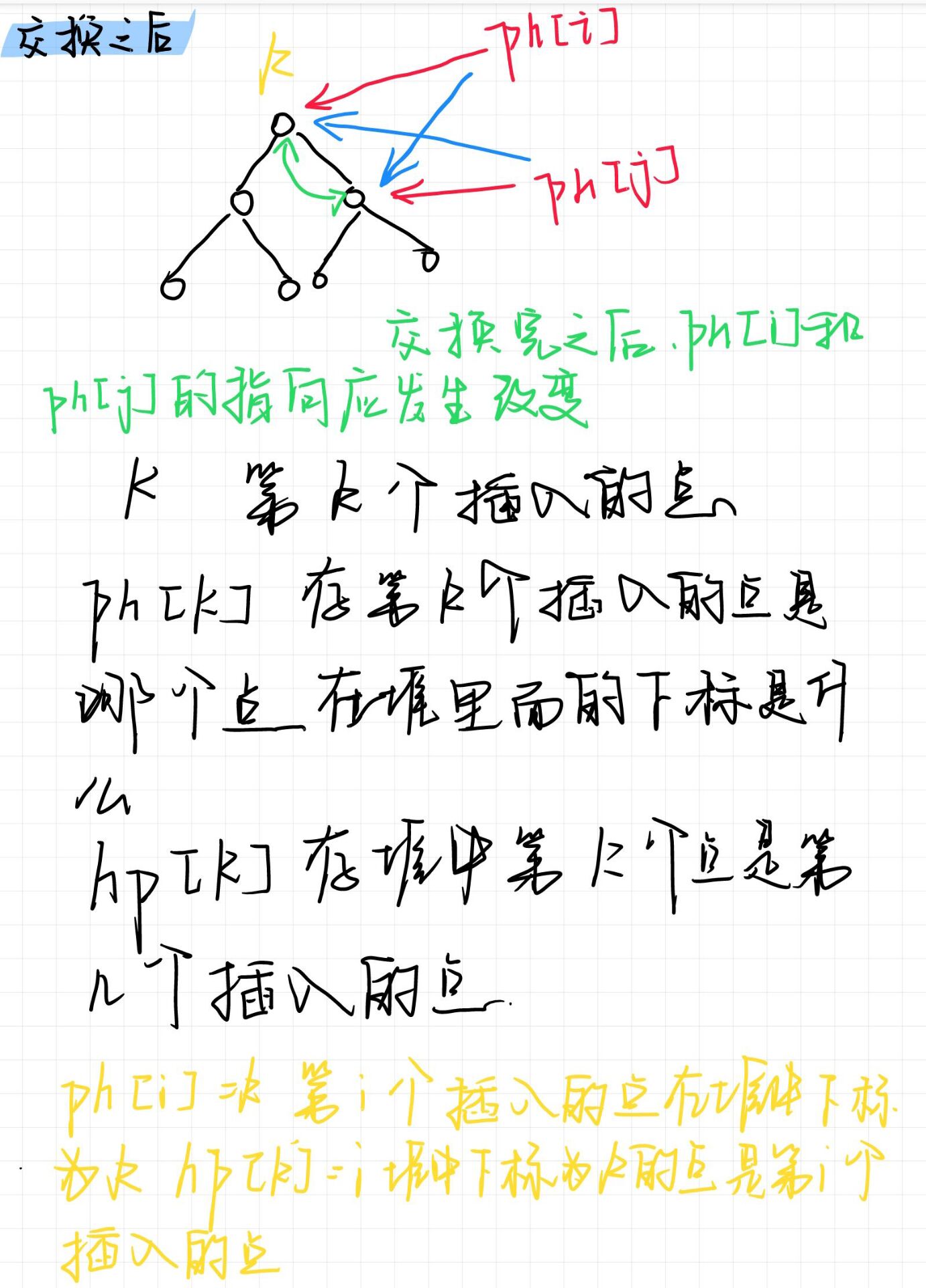
数据结构 堆
手写堆,而非stl中的堆 如何手写一个堆? //将数组建成堆 <O(n) for (int i n / 2;i;i--) //从n/2开始down down(i); 从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层…...
将 ONLYOFFICE 文档编辑器与 Node.js 应用集成
我们来了解下,如何将 ONLYOFFICE 文档编辑器与您的 Web 应用集成。 许多 Web 应用都可以从文档编辑功能中获益。但是要从头开始创建这个功能,需要花费大量时间和精力。幸运的是,您可以使用 ONLYOFFICE——这是一款开源办公套件,可…...
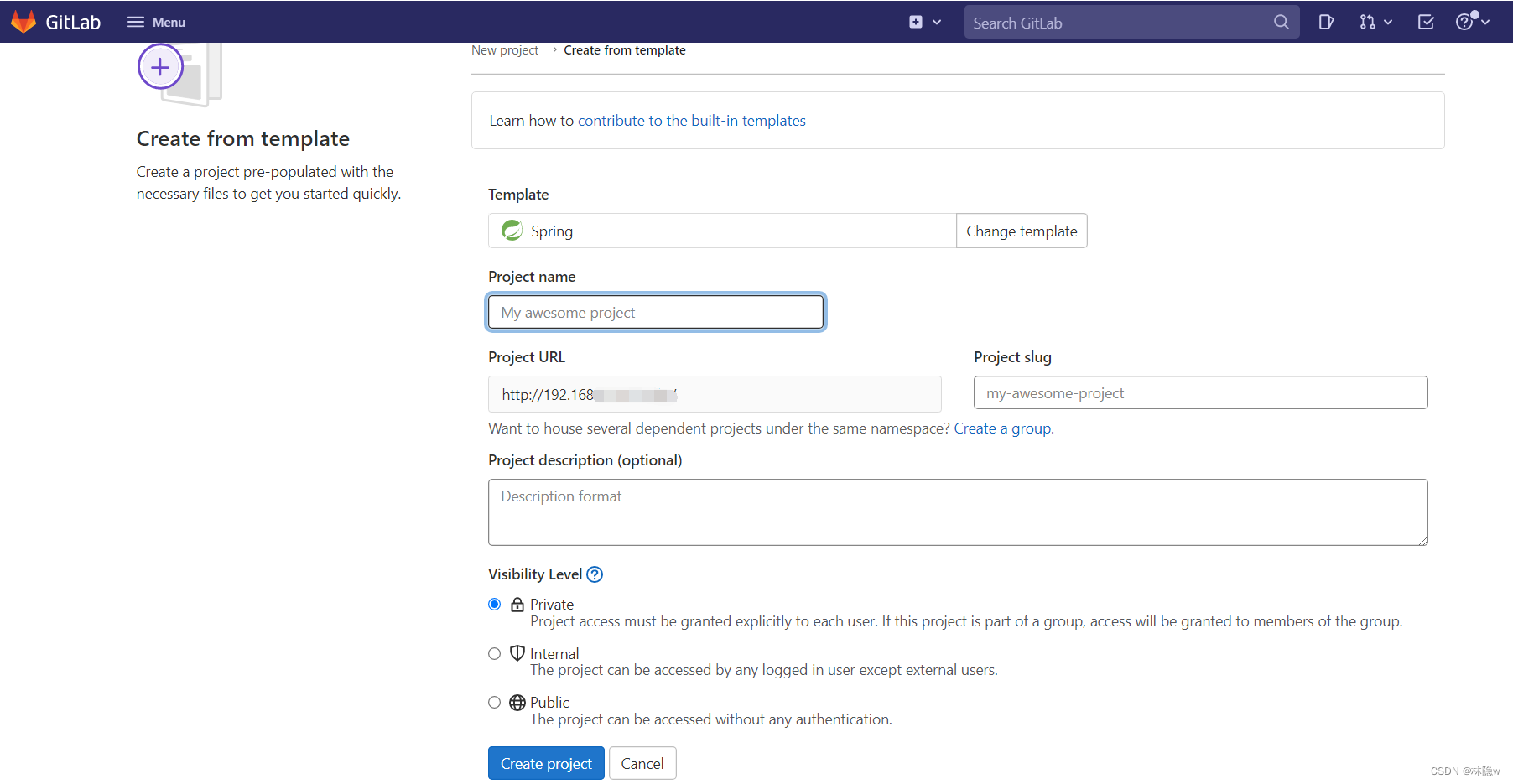
CentOS 7搭建Gitlab流程
目录 1、查询docker镜像gitlab-ce 2、拉取镜像 3、查询已下载的镜像 4、新建gitlab文件夹 5、在gitlab文件夹下新建相关文件夹 6、创建运行gitlab的容器 7、查看docker容器 8、根据Linux地址访问gitlab 9、进入docker容器,设置用户名的和密码 10、登录git…...
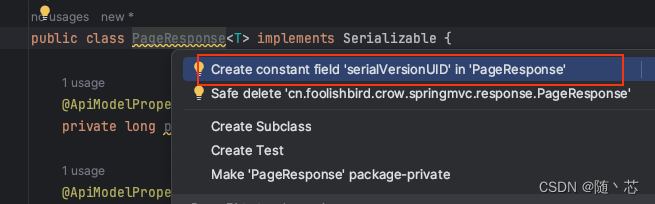
Idea安装完成配置
目录: 环境配置Java配置Maven配置Git配置 基础设置编码级设置File Header自动生成序列化编号配置 插件安装MyBtisPlusRestfulTooklkit-fix 环境配置 Java配置 Idea右上方,找到Project Settings. 有些版本直接有,有些是在设置下的二级菜单下…...

超详细~25考研规划~感恩现在努力的你!!!
25考研规划 俄语,翻译过来叫我爱你 考试时间 第一天 8.30-11.30政治——100分 2.00-5.00英语——100分 第二天 8.30-11.30数学——150分 2.00-5.00专业课——150分 1.什么是25考研 将在2024年12月参加考研,2025年本科毕业,9月读研究…...

智慧城市安全监控的新利器
在传统的城市管理中,井盖的监控一直是一个难题,而井盖异动传感器的出现为这一问题提供了有效的解决方案。它具有体积小、重量轻、安装方便等特点,可以灵活地应用于各种类型的井盖,实现对城市基础设施的全方位监控。 智能井盖监测终…...
)
【算法】石子合并(区间dp)
题目 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子…...

C++-特殊类和单例模式
1.请设计一个类,不能被拷贝 拷贝构造函数以及赋值运算符重载,因此想要让一个类禁止拷贝,只需让该类不能调用拷贝构造函数以及赋值运算符重载即可。 //该类不能发生拷贝class NonCopy{public:NonCopy(const NonCopy& Nc) delete;NonCopy&…...

【开源】基于Vue.js的智能教学资源库系统
项目编号: S 050 ,文末获取源码。 \color{red}{项目编号:S050,文末获取源码。} 项目编号:S050,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课…...

C语言之qsort()函数的模拟实现
C语言之qsort()函数的模拟实现 文章目录 C语言之qsort()函数的模拟实现1. 简介2. 冒泡排序3. 对冒泡排序进行改造4. 改造部分4.1 保留部分的冒泡排序4.2 比较部分4.3 交换部分 5. bubble_sort2完整代码6. 使用bubble_sort2来排序整型数组7. 使用bubble_sort2来排序结构体数组7.…...

数字化未来:实时云渲染在智慧城市中的创新应用
数字中国战略"是国家推动数字经济发展的战略框架。这个战略旨在加速数字化转型,推动信息技术在各个领域的应用,提高社会经济效益和人民生活质量。而智慧城市作为其中的重要一环,重要性不言而喻。 智慧城市是当今城市发展的热点和趋势&a…...
Go语言常用命令详解(二)
文章目录 前言常用命令go bug示例参数说明 go doc示例参数说明 go env示例 go fix示例 go fmt示例 go generate示例 总结写在最后 前言 接着上一篇继续介绍Go语言的常用命令 常用命令 以下是一些常用的Go命令,这些命令可以帮助您在Go开发中进行编译、测试、运行和…...

ChatGPT 从零到一打造私人智能英语学习助手
近几年,随着智能化技术的发展和人工智能的兴起,越来越多的应用程序开始涌现出来。在这些应用中,语音识别、自然语言处理以及机器翻译等技术都得到了广泛的应用。其中,聊天机器人成为了最受欢迎的人工智能应用之一,它们…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
