DAY59 503.下一个更大元素II + 42. 接雨水
503.下一个更大元素II
题目要求:
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
- 输入: [1,2,1]
- 输出: [2,-1,2]
- 解释: 第一个 1 的下一个更大的数是 2;数字 2 找不到下一个更大的数;第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
思路
可以选择扩充nums数组,或者其实也可以不扩充nums,而是在遍历的过程中模拟走了两边nums。
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {vector<int> result(nums.size(), -1);if (nums.size() == 0) return result;stack<int> st;st.push(0);for (int i = 1; i < nums.size() * 2; ++i) {if (nums[i % nums.size()] < nums[st.top()]) st.push(i % nums.size());else if (nums[i % nums.size()] == nums[st.top()]) st.push(i % nums.size());else {while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {result[st.top()] = nums[i % nums.size()];st.pop();}st.push(i % nums.size());}}return result;}
};42. 接雨水
题目要求:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

- 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 输出:6
- 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
- 输入:height = [4,2,0,3,2,5]
- 输出:9
思路
本题暴力解法也是也是使用双指针。
首先要明确,要按照行来计算,还是按照列来计算。
按照行来计算如图:
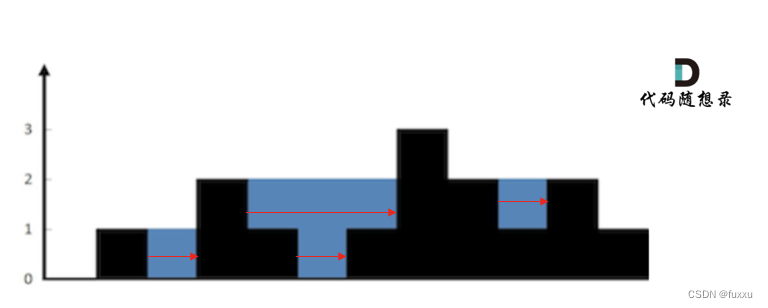
按照列来计算如图:
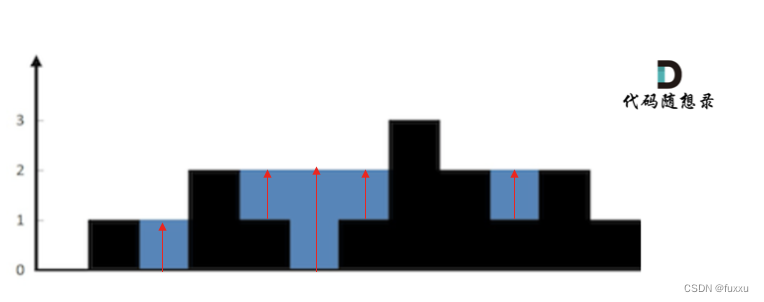
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
首先,如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。
可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
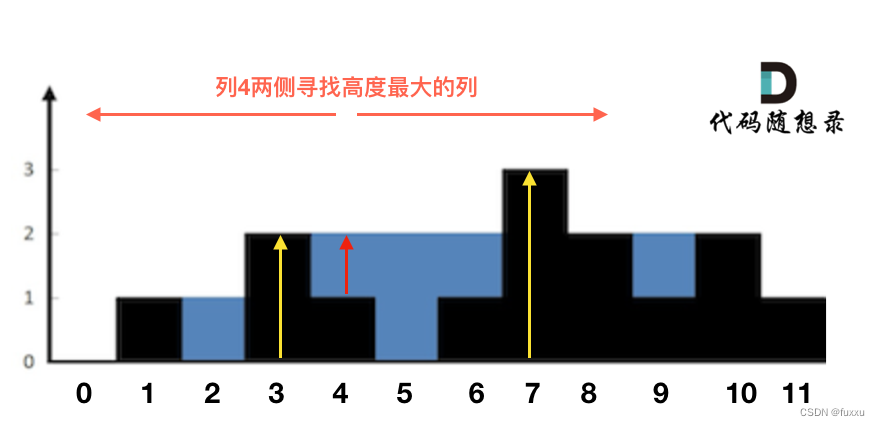
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
列4 柱子的高度为1(以下用height表示)
那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
此时求出了列4的雨水体积。
一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
首先从头遍历所有的列,并且要注意第一个柱子和最后一个柱子不接雨水,代码如下:
for (int i = 0; i < height.size(); i++) {// 第一个柱子和最后一个柱子不接雨水if (i == 0 || i == height.size() - 1) continue;
}在for循环中求左右两边最高柱子,代码如下:
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {if (height[l] > lHeight) lHeight = height[l];
}最后,计算该列的雨水高度,代码如下:
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中整体代码如下:
class Solution {
public:int trap(vector<int>& height) {int sum = 0;for (int i = 0; i < height.size(); i++) {// 第一个柱子和最后一个柱子不接雨水if (i == 0 || i == height.size() - 1) continue;int rHeight = height[i]; // 记录右边柱子的最高高度int lHeight = height[i]; // 记录左边柱子的最高高度for (int r = i + 1; r < height.size(); r++) {if (height[r] > rHeight) rHeight = height[r];}for (int l = i - 1; l >= 0; l--) {if (height[l] > lHeight) lHeight = height[l];}int h = min(lHeight, rHeight) - height[i];if (h > 0) sum += h;}return sum;}
};因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2),空间复杂度为O(1)。
力扣后面修改了后台测试数据,所以以上暴力解法超时了。
单调栈解法
单调栈就是保持栈内元素有序。通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
而接雨水这道题目,我们正需要寻找一个元素,右边最大元素以及左边最大元素,来计算雨水面积。
准备工作
那么本题使用单调栈有如下几个问题:
1. 首先单调栈是按照行方向来计算雨水,如图:

知道这一点,后面的就可以理解了。
2. 使用单调栈内元素的顺序
从大到小还是从小到大呢?
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
如图:

3. 遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
如图所示:
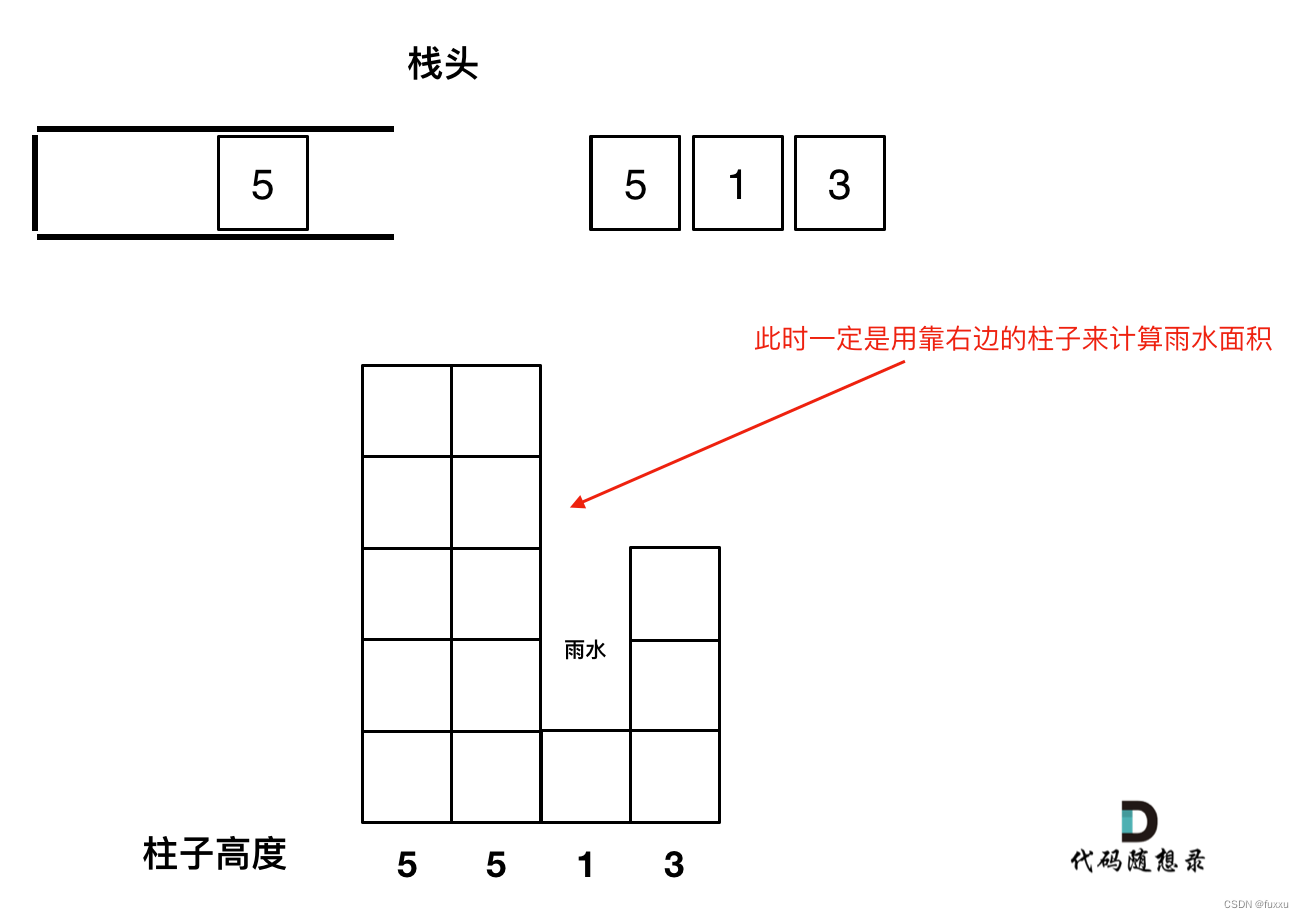
4. 栈里要保存什么数值
使用单调栈,也是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,
那么栈里有没有必要存一个pair<int, int>类型的元素,保存柱子的高度和下标呢。
其实不用,栈里就存放下标就行,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下:
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度明确了如上几点,我们再来看处理逻辑。
单调栈处理逻辑
以下逻辑主要就是三种情况
- 情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
- 情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
- 情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
先将下标0的柱子加入到栈中,st.push(0);。 栈中存放我们遍历过的元素,所以先将下标0加进来。
然后开始从下标1开始遍历所有的柱子,for (int i = 1; i < height.size(); i++)。
如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
代码如下:
if (height[i] < height[st.top()]) st.push(i);如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
代码如下:
if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况st.pop();st.push(i);
}如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
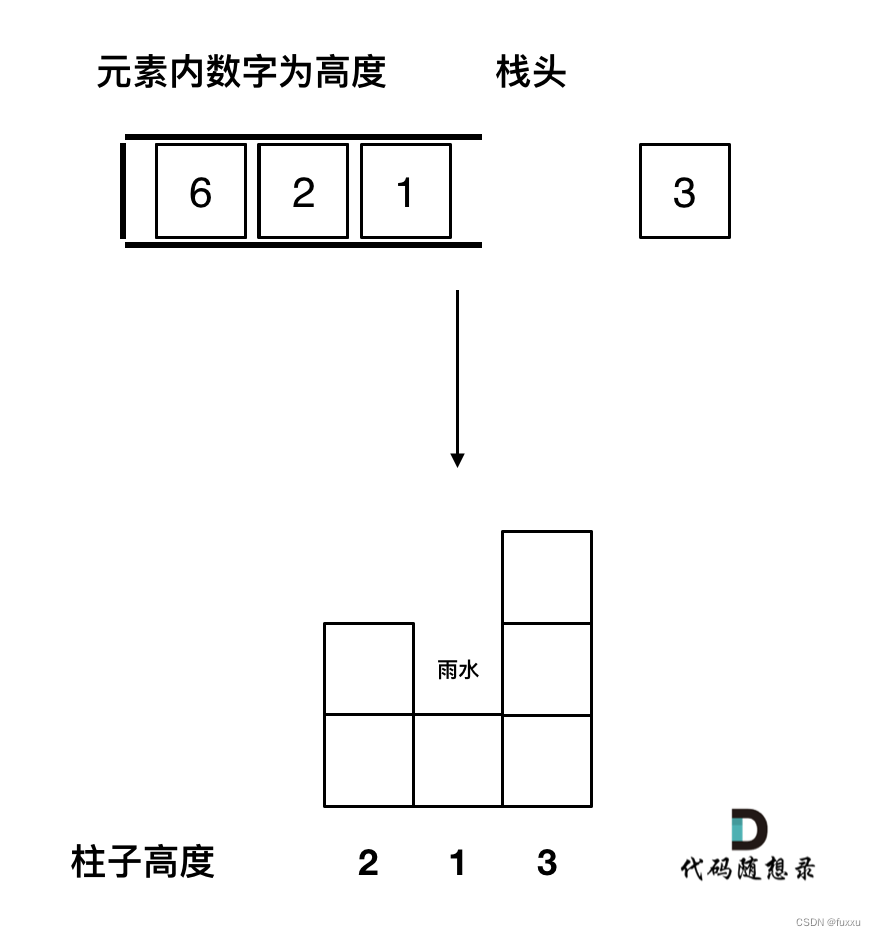
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的元素,三个元素来接水!
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:int h = min(height[st.top()], height[i]) - height[mid];
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:int w = i - st.top() - 1 ;
当前凹槽雨水的体积就是:h * w。
求当前凹槽雨水的体积代码如下:
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素int mid = st.top();st.pop();if (!st.empty()) {int h = min(height[st.top()], height[i]) - height[mid];int w = i - st.top() - 1; // 注意减一,只求中间宽度sum += h * w;}
}class Solution {
public:int trap(vector<int>& height) {if (height.size() <= 2) return 0;stack<int> st;st.push(0);int sum = 0;for (int i = 1; i < height.size(); ++i) {if (height[i] < height[st.top()]) {st.push(i);} else if (height[i] == height[st.top()]) {st.pop();st.push(i);} else {while (!st.empty() && height[i] > height[st.top()]) {int mid = st.top();st.pop();if (!st.empty()) {int h = min(height[st.top()], height[i]) - height[mid];int w = i - st.top() - 1;sum += h * w;}}st.push(i);}}return sum;}
};相关文章:

DAY59 503.下一个更大元素II + 42. 接雨水
503.下一个更大元素II 题目要求: 给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数&am…...

【如何将任何直流电机变成伺服电机】
【如何将任何直流电机变成伺服电机】 1 前沿2 伺服电机工作原理3 如何制作定制伺服电机4 AS5600 编码器 – 磁性旋转位置传感器5 定制伺服电机电路图6 PCB设计7 自定义伺服3D模型8 定制伺服齿轮箱的 3D 打印零件9 对控制器进行编程9.1 引导加载程序刻录9.2 代码上传9.3 源代码9…...

单片机语音芯片在工业控制中的应用优势
单片机语音芯片,这一智能化的代表产品,不仅在家庭和消费电子领域发挥着重要的作用,更为工业控制领域注入了新的活力。将单片机语音芯片与语音交互技术相结合,为工业设备的控制和监测提供了前所未有的解决方案。 首先,…...

【开源】基于Vue.js的高校实验室管理系统的设计和实现
项目编号: S 015 ,文末获取源码。 \color{red}{项目编号:S015,文末获取源码。} 项目编号:S015,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 实验室类型模块2.2 实验室模块2.3 实…...

Xrdp+内网穿透实现远程访问Linux Kali桌面
XrdpCpolar实现远程访问Linux Kali桌面 文章目录 XrdpCpolar实现远程访问Linux Kali桌面前言1. Kali 安装Xrdp2. 本地远程Kali桌面3. Kali 安装Cpolar 内网穿透4. 配置公网远程地址5. 公网远程Kali桌面连接6. 固定连接公网地址7. 固定地址连接测试 前言 Kali远程桌面的好处在于…...

【洛谷算法题】P5713-洛谷团队系统【入门2分支结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5713-洛谷团队系统【入门2分支结构】🌏题目描述🌏输入格…...
Eclipse切换中文环境
PACK包链接 地址,进入后可以看到不同版本的包。 要选择跟自己Eclipse版本一致的包,比如我的Eclipse启动界面如下,我就要找Helios的包( Juno、Indigo、Helios、Kepler这些具体怎么划分的我也不清楚)。 在线安装 打…...

栈和队列概念
栈stack 栈只能在一端插入/删除元素先入后出只能从栈顶插入,栈顶删除栈底不允许插入和删除push:进栈pop:出栈应用场景: 队列 Queue 队列的插入操作称为 “入队”(Enqueue),是在队尾进行的&am…...
a标签下载文件与解决浏览器默认打开某些格式文件的问题
前言 在实际项目中,我们通常会遇到这么一个需求:后端给前端返回一个任意文件类型的完整的url路径,前端拿到这个路径直接通过浏览器下载文件到本地。我想大家应该都会首先想到使用HTML中的<a>标签,,因为<a>…...

EasyCVR视频监控+AI智能分析网关如何助力木材厂安全生产?
旭帆科技有很多工厂的视频监管方案,小编也经常分享出来供大家参考。近期,又有伙伴后台私信我们想要关于木材厂的方案。针对木材厂的生产过程与特性以及安全风险等,我们来分享一下相关的监管方案: 1)温湿度监测…...
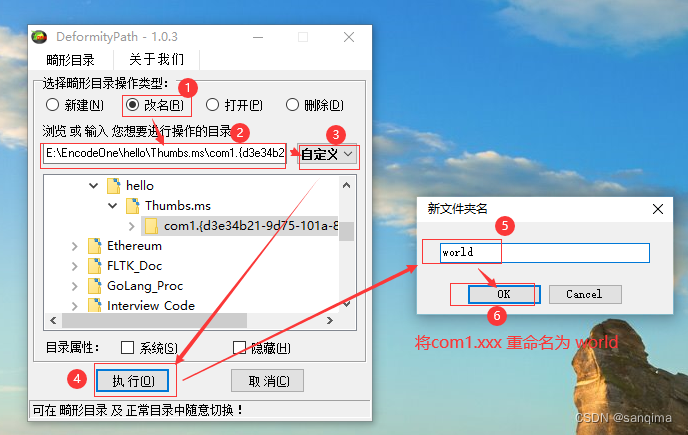
重命名com1.{d3e34b21-9d75-101a-8c3d-00aa001a1652}文件夹
今天在win10系统上,发现一个名称为: com1.{d3e34b21-9d75-101a-8c3d-00aa001a1652} 的文件夹,该文件夹很奇怪,既不能手动删除,也不能手动给文件夹重命名,如图(1)所示: E:\EncodeOne\hello\Thumbs.ms\com1.…...

springboot+activiti5.22.0集成Activiti在线流程设计器
SpringBoot集成Activiti5.22在线流程设计器 文章目录 SpringBoot集成Activiti5.22在线流程设计器📝1.增加配置pom依赖 增加数据库及redis配置文件📜 2.启动类ActivitiDesignApplication排除安全校验注解启动项目后将会自动在数据库中生成表 📘…...

pdf如何让多张图片在一页
pdf保存为一页六张图片的方法是: 1、打开pdf查看器,打开文档。 2、点击【打印】图标进入打印程序,选择打印范围。 3、在【打印处理】选项,选择【每张张上放置多页】。 4、自定义每页放置的图片张数为六张,并对打印排版预览设置。 5、设置打印…...

【C语言_题库】输入4个整数,要求按照从小到大的顺序输出
题目 输入4个整数 要求按照从小到大的顺序输出 书上的学习辅导答案 // 主要部分 int main(){int t,a,b,c,d;printf("请输入四个数:");scanf("%d,%d,%d,%d"...

Cascade-MVSNet论文笔记
Cascade-MVSNet论文笔记 摘要1 立体匹配(Stereo Matching)2 多视图立体视觉(Multi-View Stereo)3 立体视觉和立体视觉的高分辨率输出4 代价体表达方式(Cost volume Formulation)4.1 多视图立体视觉的3D代价…...
Linux调试器---gdb的使用
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 键盘敲烂,年薪百万! 一、gdb的背景 gdb,全称为GNU调试器(GNU Debugger),是一个功能强大的源代码级调试工具,主要…...
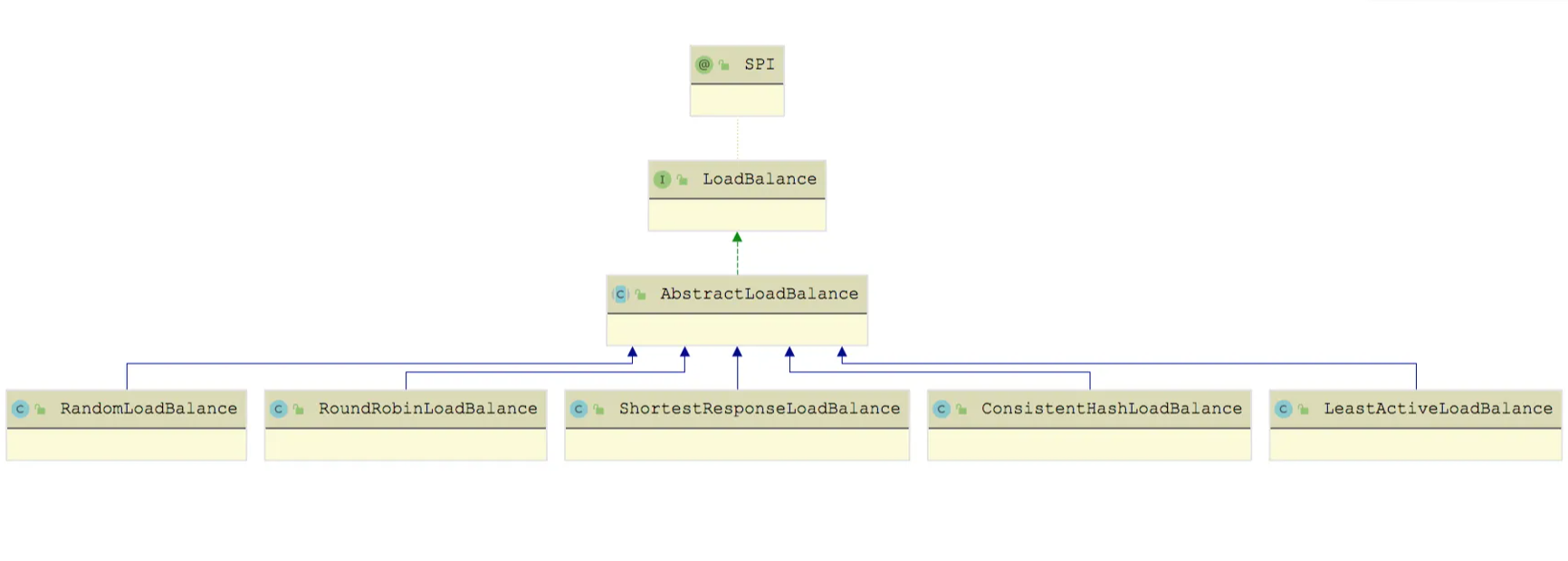
【Dubbo】Dubbo负载均衡实现解析
📫作者简介:小明java问道之路,2022年度博客之星全国TOP3,专注于后端、中间件、计算机底层、架构设计演进与稳定性建设优化,文章内容兼具广度、深度、大厂技术方案,对待技术喜欢推理加验证,就职于…...

怎样备份电脑文件比较安全
域智盾软件是一款功能强大的电脑监控软件,它不仅具备实时屏幕监控、行为审计等功能,还能够对电脑文件进行备份和管理。下面将介绍域智盾软件如何备份电脑文件,以确保数据安全。 1、开启文档备份功能 部署后台,然后点击文档安全&a…...

python 计算最大回撤
1. 什么是最大回撤 最大回撤是评估金融产品收益的一个非常重要的风险指标,它指的是在选定历史周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值。 以上图为例, 最大回撤 ( V a l u e A − V a l u e B ) V a l u e …...

Linux系统中常用的压缩与解压缩方法
目录 一.前言二.如何压缩与解压缩 一.前言 Linux系统中压缩和解压缩的方法很多,这篇文章只简单介绍一下使用tar和gzip进行压缩与解压缩。 二.如何压缩与解压缩 tar和gzip命令内容很多,这篇文章只是简单介绍一下。 1.看一下gzip命令压缩与解压缩方法。…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
