a标签下载文件与解决浏览器默认打开某些格式文件的问题
前言
在实际项目中,我们通常会遇到这么一个需求:后端给前端返回一个任意文件类型的完整的url路径,前端拿到这个路径直接通过浏览器下载文件到本地。我想大家应该都会首先想到使用HTML中的<a>标签,,因为<a>标签中提供download属性,使得流量拿起将链接url视为下载资源。
然后我想记录此篇文章的主要原因是,在使用<a>标签下载文件时,由于浏览器默认行为,对于一些特殊格式的文件比如:txt,png,jpg等文件这些浏览器支持直接打开的文件是不会执行下载任务的,而是会直接打开文件。因此,本文主要先讲一下<a>下载文件的用法,后面也会给出对于特殊文件时浏览器直接打开的解决方式。
<a>元素介绍
<a>元素(或称锚元素),可以通过它的href属性创建通向其他网页、文件、电子邮件地址、同一页面内的位置或者其他URL的超链接
属性
download
导致浏览器将链接URL视为下载资源。可以使用或不适用filename值:
- 如果没有指定值,浏览器会从多个来源决定文件名和扩展名:
- Content-Disposition HTTP标头
- URL 路径的最后一段
- 媒体类,来自Content-Type标头,data:URL的开头,或者blob:URL的Blob.type
- filename:决定文件名的值。/和\被转换为下划线( _ )。文件系统可能会阻止文件名中其他的字符,因此浏览器会在必要时适当调整文件名。
href
超链接所指向的URL。链接不限于基于HTTP的URL------它们可以使用浏览器支持任何URL的协议:
- 使用文档片段链接到页面的某一段
- 使用文本片段链接到某一段文字
- 使用媒体片段链接到某个媒体文件
- 使用
tel:URL 链接到一个电话号码 - 使用
mailto:URL 链接到一个邮箱地址 - 如果 web 浏览器不能支持其他 URL 协议,网站可以使用 registerProtocolHandler()
target
该属性指定在何处显示链接URL,作为浏览器上下文的名称(标签、窗口或者<iframe>)。以下关键字对加载的URL的位置有特殊含义:
- _self:当前页面加载(默认)
- _blank:通常在新标签页打开,但用户可以通过配置选择在新窗口打开
- _parent:当前浏览环境的父级浏览上下文。如果没有父级框架,行为与_self相同
- _top:最顶级的浏览上下文(当前浏览上下文中最“高”的祖先),如果没有祖先,行为与_self相同。
我在这里主要介绍几个我常用到的属性,但是<a>还有很多其他属性,感兴趣的话可以在这里进行详细的了解<a>:锚元素 - HTML(超文本标记语言) | MDN
使用<a>元素下载文件遇到的问题
这里我要说明一下我使用<a>元素下载文件时遇到的问题:chrome浏览器中会打开支持预览的文件(比如前面提到的:txt,png,jpg等),而不是直接下载。然后我也看到一些人给出的方法是说给a标签加一个“download”属性,但是不知道为啥,我试了是不行的。
然后我又找到如下可以有效解决该问题的方式:
解决方式1:设置Content-type
chrome浏览器对与txt,json等文件直接打开应该是浏览器对这些类型的文件支持预览,可以设置Content-type:application/octet-stream来解决此问题,即告诉浏览器这是一个字节流,浏览器处理字节流的默认方式是下载,以下是我需要使用到的一些文件格式,并对其进行处理,还有很多其他文件格式,拼接的类型 会有所差别,可以详细查看这份:如何设置Content-Type(MIME)_对象存储 OSS-阿里云帮助中心
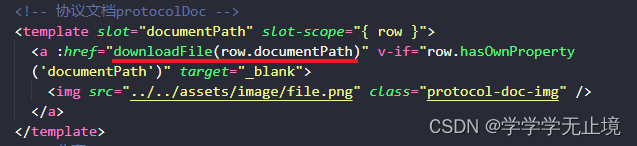
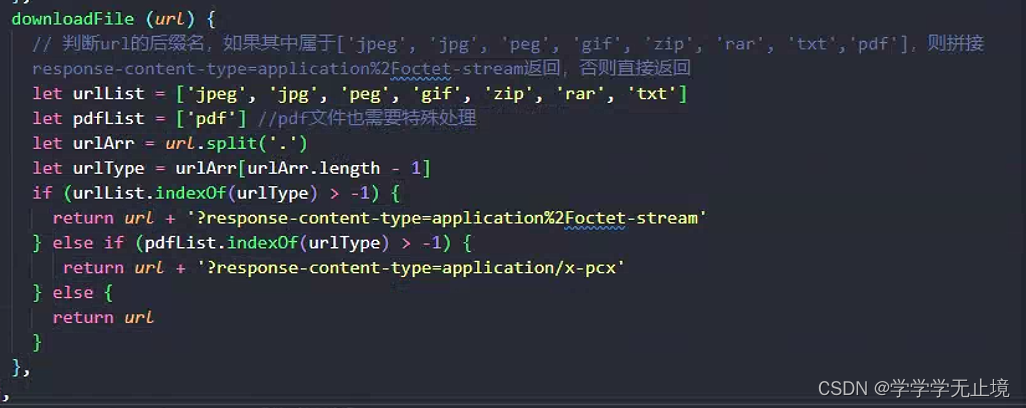
解决方法2:使用ajax请求该url,获取到文本内容,手动实现下载。
可以参开这个博主这篇文章:使用a标签下载文件,浏览器会直接打开解决方案_a标签下载图片会打开-CSDN博客
相关文章:

a标签下载文件与解决浏览器默认打开某些格式文件的问题
前言 在实际项目中,我们通常会遇到这么一个需求:后端给前端返回一个任意文件类型的完整的url路径,前端拿到这个路径直接通过浏览器下载文件到本地。我想大家应该都会首先想到使用HTML中的<a>标签,,因为<a>…...

EasyCVR视频监控+AI智能分析网关如何助力木材厂安全生产?
旭帆科技有很多工厂的视频监管方案,小编也经常分享出来供大家参考。近期,又有伙伴后台私信我们想要关于木材厂的方案。针对木材厂的生产过程与特性以及安全风险等,我们来分享一下相关的监管方案: 1)温湿度监测…...
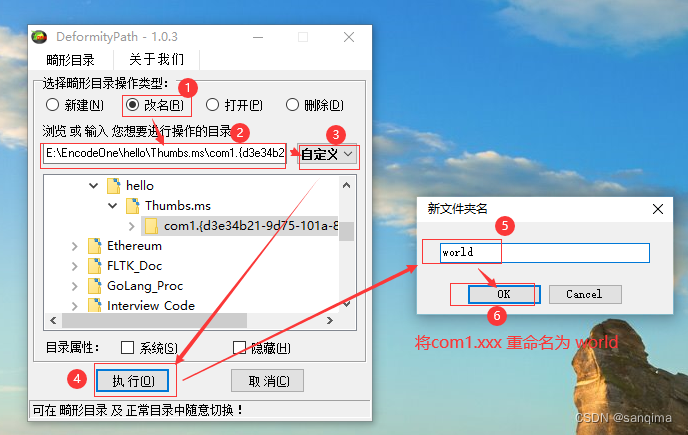
重命名com1.{d3e34b21-9d75-101a-8c3d-00aa001a1652}文件夹
今天在win10系统上,发现一个名称为: com1.{d3e34b21-9d75-101a-8c3d-00aa001a1652} 的文件夹,该文件夹很奇怪,既不能手动删除,也不能手动给文件夹重命名,如图(1)所示: E:\EncodeOne\hello\Thumbs.ms\com1.…...

springboot+activiti5.22.0集成Activiti在线流程设计器
SpringBoot集成Activiti5.22在线流程设计器 文章目录 SpringBoot集成Activiti5.22在线流程设计器📝1.增加配置pom依赖 增加数据库及redis配置文件📜 2.启动类ActivitiDesignApplication排除安全校验注解启动项目后将会自动在数据库中生成表 📘…...

pdf如何让多张图片在一页
pdf保存为一页六张图片的方法是: 1、打开pdf查看器,打开文档。 2、点击【打印】图标进入打印程序,选择打印范围。 3、在【打印处理】选项,选择【每张张上放置多页】。 4、自定义每页放置的图片张数为六张,并对打印排版预览设置。 5、设置打印…...

【C语言_题库】输入4个整数,要求按照从小到大的顺序输出
题目 输入4个整数 要求按照从小到大的顺序输出 书上的学习辅导答案 // 主要部分 int main(){int t,a,b,c,d;printf("请输入四个数:");scanf("%d,%d,%d,%d"...

Cascade-MVSNet论文笔记
Cascade-MVSNet论文笔记 摘要1 立体匹配(Stereo Matching)2 多视图立体视觉(Multi-View Stereo)3 立体视觉和立体视觉的高分辨率输出4 代价体表达方式(Cost volume Formulation)4.1 多视图立体视觉的3D代价…...
Linux调试器---gdb的使用
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 键盘敲烂,年薪百万! 一、gdb的背景 gdb,全称为GNU调试器(GNU Debugger),是一个功能强大的源代码级调试工具,主要…...
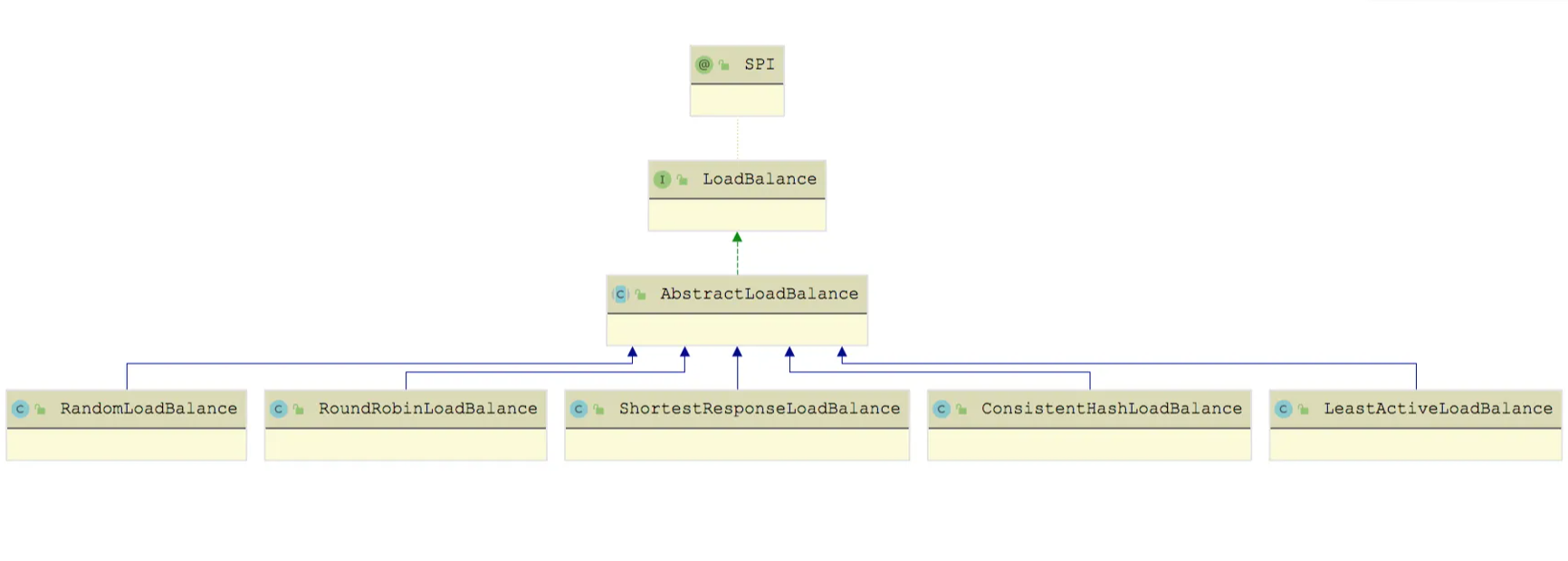
【Dubbo】Dubbo负载均衡实现解析
📫作者简介:小明java问道之路,2022年度博客之星全国TOP3,专注于后端、中间件、计算机底层、架构设计演进与稳定性建设优化,文章内容兼具广度、深度、大厂技术方案,对待技术喜欢推理加验证,就职于…...

怎样备份电脑文件比较安全
域智盾软件是一款功能强大的电脑监控软件,它不仅具备实时屏幕监控、行为审计等功能,还能够对电脑文件进行备份和管理。下面将介绍域智盾软件如何备份电脑文件,以确保数据安全。 1、开启文档备份功能 部署后台,然后点击文档安全&a…...

python 计算最大回撤
1. 什么是最大回撤 最大回撤是评估金融产品收益的一个非常重要的风险指标,它指的是在选定历史周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值。 以上图为例, 最大回撤 ( V a l u e A − V a l u e B ) V a l u e …...

Linux系统中常用的压缩与解压缩方法
目录 一.前言二.如何压缩与解压缩 一.前言 Linux系统中压缩和解压缩的方法很多,这篇文章只简单介绍一下使用tar和gzip进行压缩与解压缩。 二.如何压缩与解压缩 tar和gzip命令内容很多,这篇文章只是简单介绍一下。 1.看一下gzip命令压缩与解压缩方法。…...
)
目标检测YOLO实战应用案例100讲-基于机器视觉的水稻病虫害监测预警(续)
目录 3.3 试验结果与分析 3.3.1 数据集介绍 3.3.3 评价标准 3.3.4 模型训练参数设置...

【星海随笔】redis 解析
redis 非关系型数据库 支持事务,操作都是原子性 所谓的原子性就是对数据的更改要么全部执行,要么全部不执行。 redis-server:顾名思义,redis服务 redis-cli:redis client,提供一个redis客户端,…...
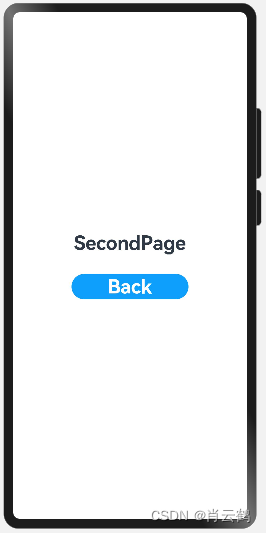
鸿蒙:实现两个Page页面跳转
效果展示 这篇博文在《鸿蒙:从0到“Hello Harmony”》基础上实现两个Page页面跳转 1.构建第一个页面 第一个页面就是“Hello Harmony”,把文件名和显示内容都改一下,改成“FirstPage”,再添加一个“Next”按钮。 Entry Compone…...

C#有关里氏替换原则的经典问题答疑
目录 理解创建类型与变量类型很关键 先来理解变量类型。 再来理解创建类型。 有了正确的理解再来看疑问 里氏替换原则是面向对象七大原则中最重要的原则。 语法表现:父类容器装子类对象。 namespace 里氏替换原则 {class GameObject { } class Player : GameO…...
【每日一题】689. 三个无重叠子数组的最大和-2023.11.19
题目: 689. 三个无重叠子数组的最大和 给你一个整数数组 nums 和一个整数 k ,找出三个长度为 k 、互不重叠、且全部数字和(3 * k 项)最大的子数组,并返回这三个子数组。 以下标的数组形式返回结果,数组中…...

“开源 vs. 闭源:大模型的未来发展趋势预测“——探讨大模型未来的发展方向
文章目录 每日一句正能量前言什么是大模型的开源与闭源开源与闭源的定义和特点开源的意义开源和闭源的优劣势比较不同的大模型企业,开源、闭源的策略不尽相同。企业在开发垂类模型时选择开源还是闭源大模型开源vs 闭源:两者并非选择题后记 每日一句正能量…...

计算机网络——物理层-信道的极限容量(奈奎斯特公式、香农公式)
目录 介绍 奈氏准则 香农公式 介绍 信号在传输过程中,会受到各种因素的影响。 如图所示,这是一个数字信号。 当它通过实际的信道后,波形会产生失真;当失真不严重时,在输出端还可根据已失真的波形还原出发送的码元…...

【算法挨揍日记】day31——673. 最长递增子序列的个数、646. 最长数对链
673. 最长递增子序列的个数 673. 最长递增子序列的个数 题目解析: 给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。 注意 这个数列必须是 严格 递增的。 解题思路: 算法思路: 1. 状态表⽰: 先尝试…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
