python 计算最大回撤
1. 什么是最大回撤
最大回撤是评估金融产品收益的一个非常重要的风险指标,它指的是在选定历史周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值。

以上图为例, 最大回撤 = ( V a l u e A − V a l u e B ) V a l u e A 最大回撤 = \frac{(ValueA - ValueB) } {ValueA} 最大回撤=ValueA(ValueA−ValueB)
2. 计算最大回撤
下面演示使用pandas 计算最大回撤
- 获取贵州茅台20191.1到2019.12.31的日k数据
import pandas as pd
import numpy as np
import baostock as bslg = bs.login()
# 显示登陆返回信息
print('login respond error_code:'+lg.error_code)
print('login respond error_msg:'+lg.error_msg)#### 获取沪深A股历史K线数据 ####
# 详细指标参数,参见“历史行情指标参数”章节;“分钟线”参数与“日线”参数不同。“分钟线”不包含指数。
# 分钟线指标:date,time,code,open,high,low,close,volume,amount,adjustflag
# 周月线指标:date,code,open,high,low,close,volume,amount,adjustflag,turn,pctChg
rs = bs.query_history_k_data_plus("sh.600519","date,code,open,high,low,close,volume",start_date='2019-01-01', end_date='2019-12-31',frequency="d", adjustflag="3")
print('query_history_k_data_plus respond error_code:'+ rs.error_code)
print('query_history_k_data_plus respond error_msg:'+ rs.error_msg)data_list = []
while (rs.error_code == '0') & rs.next():# 获取一条记录,将记录合并在一起data_list.append(rs.get_row_data())
result = pd.DataFrame(data_list, columns=rs.fields)#### 结果集输出到csv文件 ####
result.to_csv("贵州茅台_k_data.csv", index=False)
print(result)#### 登出系统 ####
bs.logout()

2. 读取贵州茅台的日k数据,读入日期和收盘价
data = pd.read_csv("贵州茅台_k_data.csv")[["date", "close"]];
3.计算每天的回撤值
# 找出当前值以前的最大值
data["previous_max"] = data["close"].cummax(axis=0)
# 计算每一天的回撤
data['draw_downs'] = data['close'] / data['previous_max'] - 1
4.可视化
data.plot(y=['close','previous_max'], figsize=(8,4))

# 绘制回撤曲线
data.plot(y='draw_downs',figsize=(8,4),color='g')

5.计算最大回撤
# 最大回撤
data['draw_downs'].min()
相关文章:

python 计算最大回撤
1. 什么是最大回撤 最大回撤是评估金融产品收益的一个非常重要的风险指标,它指的是在选定历史周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值。 以上图为例, 最大回撤 ( V a l u e A − V a l u e B ) V a l u e …...

Linux系统中常用的压缩与解压缩方法
目录 一.前言二.如何压缩与解压缩 一.前言 Linux系统中压缩和解压缩的方法很多,这篇文章只简单介绍一下使用tar和gzip进行压缩与解压缩。 二.如何压缩与解压缩 tar和gzip命令内容很多,这篇文章只是简单介绍一下。 1.看一下gzip命令压缩与解压缩方法。…...
)
目标检测YOLO实战应用案例100讲-基于机器视觉的水稻病虫害监测预警(续)
目录 3.3 试验结果与分析 3.3.1 数据集介绍 3.3.3 评价标准 3.3.4 模型训练参数设置...

【星海随笔】redis 解析
redis 非关系型数据库 支持事务,操作都是原子性 所谓的原子性就是对数据的更改要么全部执行,要么全部不执行。 redis-server:顾名思义,redis服务 redis-cli:redis client,提供一个redis客户端,…...
鸿蒙:实现两个Page页面跳转
效果展示 这篇博文在《鸿蒙:从0到“Hello Harmony”》基础上实现两个Page页面跳转 1.构建第一个页面 第一个页面就是“Hello Harmony”,把文件名和显示内容都改一下,改成“FirstPage”,再添加一个“Next”按钮。 Entry Compone…...

C#有关里氏替换原则的经典问题答疑
目录 理解创建类型与变量类型很关键 先来理解变量类型。 再来理解创建类型。 有了正确的理解再来看疑问 里氏替换原则是面向对象七大原则中最重要的原则。 语法表现:父类容器装子类对象。 namespace 里氏替换原则 {class GameObject { } class Player : GameO…...
【每日一题】689. 三个无重叠子数组的最大和-2023.11.19
题目: 689. 三个无重叠子数组的最大和 给你一个整数数组 nums 和一个整数 k ,找出三个长度为 k 、互不重叠、且全部数字和(3 * k 项)最大的子数组,并返回这三个子数组。 以下标的数组形式返回结果,数组中…...

“开源 vs. 闭源:大模型的未来发展趋势预测“——探讨大模型未来的发展方向
文章目录 每日一句正能量前言什么是大模型的开源与闭源开源与闭源的定义和特点开源的意义开源和闭源的优劣势比较不同的大模型企业,开源、闭源的策略不尽相同。企业在开发垂类模型时选择开源还是闭源大模型开源vs 闭源:两者并非选择题后记 每日一句正能量…...

计算机网络——物理层-信道的极限容量(奈奎斯特公式、香农公式)
目录 介绍 奈氏准则 香农公式 介绍 信号在传输过程中,会受到各种因素的影响。 如图所示,这是一个数字信号。 当它通过实际的信道后,波形会产生失真;当失真不严重时,在输出端还可根据已失真的波形还原出发送的码元…...

【算法挨揍日记】day31——673. 最长递增子序列的个数、646. 最长数对链
673. 最长递增子序列的个数 673. 最长递增子序列的个数 题目解析: 给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。 注意 这个数列必须是 严格 递增的。 解题思路: 算法思路: 1. 状态表⽰: 先尝试…...
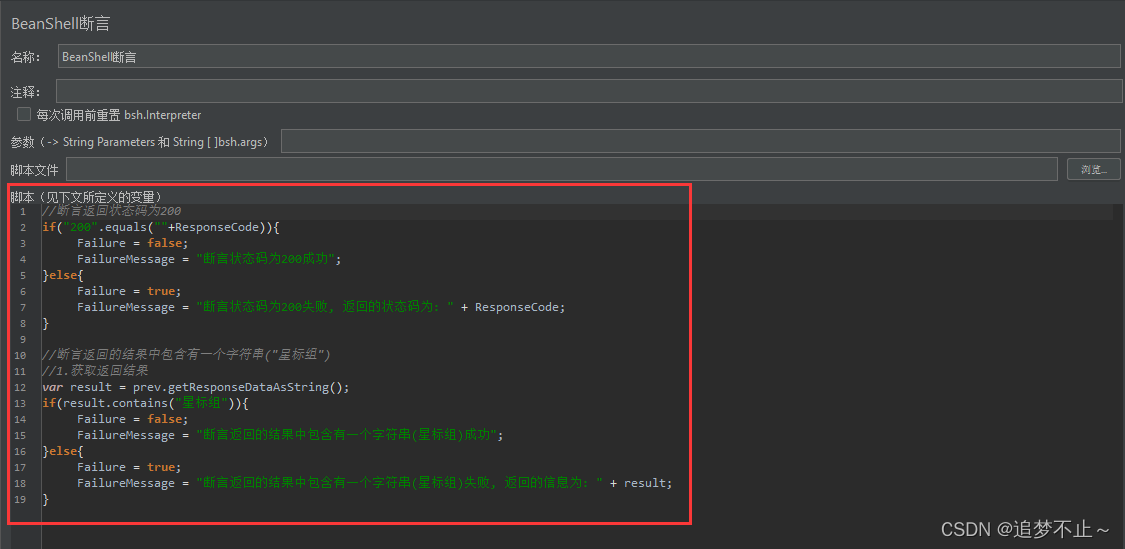
Jmeter做接口测试
1.Jmeter的安装以及环境变量的配置 Jmeter是基于java语法开发的接口测试以及性能测试的工具。 jdk:17 (最新的Jeknins,只能支持到17) jmeter:5.6 官网:http://jmeter.apache.org/download_jmeter.cgi 认识JMeter的目录࿱…...

第14届蓝桥杯青少组python试题解析:23年5月省赛
选择题 T1. 执行以下代码,输出结果是()。 lst "abc" print(lstlst)abcabc abc lstlst abcabc T2. 执行以下代码,输出的结果是()。 age {16,18,17} print(type(sorted(age)))<class set&…...
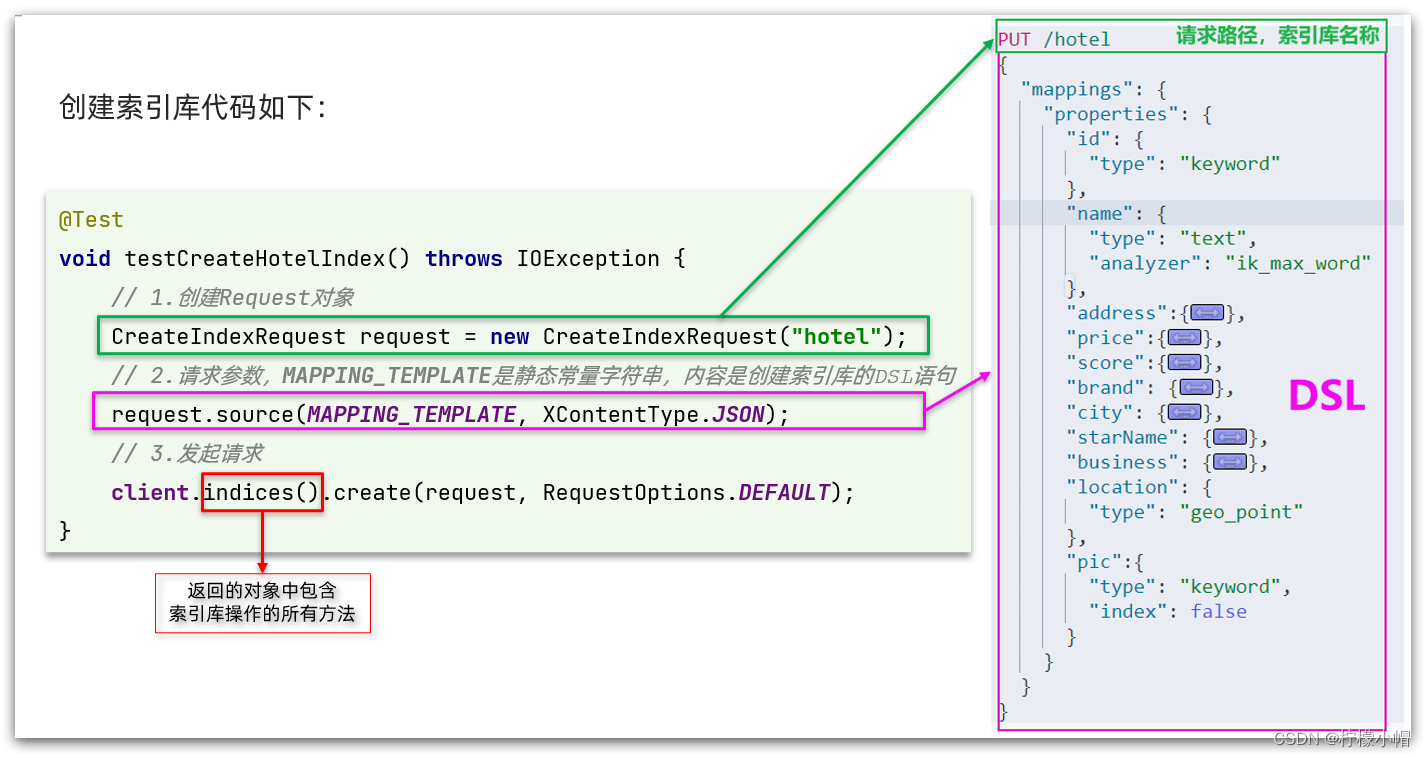
SpringCloud 微服务全栈体系(十四)
第十一章 分布式搜索引擎 elasticsearch 四、RestAPI ES 官方提供了各种不同语言的客户端,用来操作 ES。这些客户端的本质就是组装 DSL 语句,通过 http 请求发送给 ES。官方文档地址:https://www.elastic.co/guide/en/elasticsearch/client/…...

【开题报告】基于微信小程序的个人健康管理系统的设计与实现
1.选题背景与意义 在现代社会,人们对健康的关注日益增加。随着生活方式的变化和工作压力的增加,许多人意识到保持良好的身体健康对于提高生活质量和幸福感的重要性。 然而,许多人在日常生活中缺乏对自身健康状况的了解和管理。他们可能没有…...

Swagger笔记
一、导包 <!--引入swagger--> <dependency><groupId>io.springfox</groupId><artifactId>springfox-swagger2</artifactId><version>2.9.2</version> </dependency> <!--前端的UI界面--> <dependency><…...
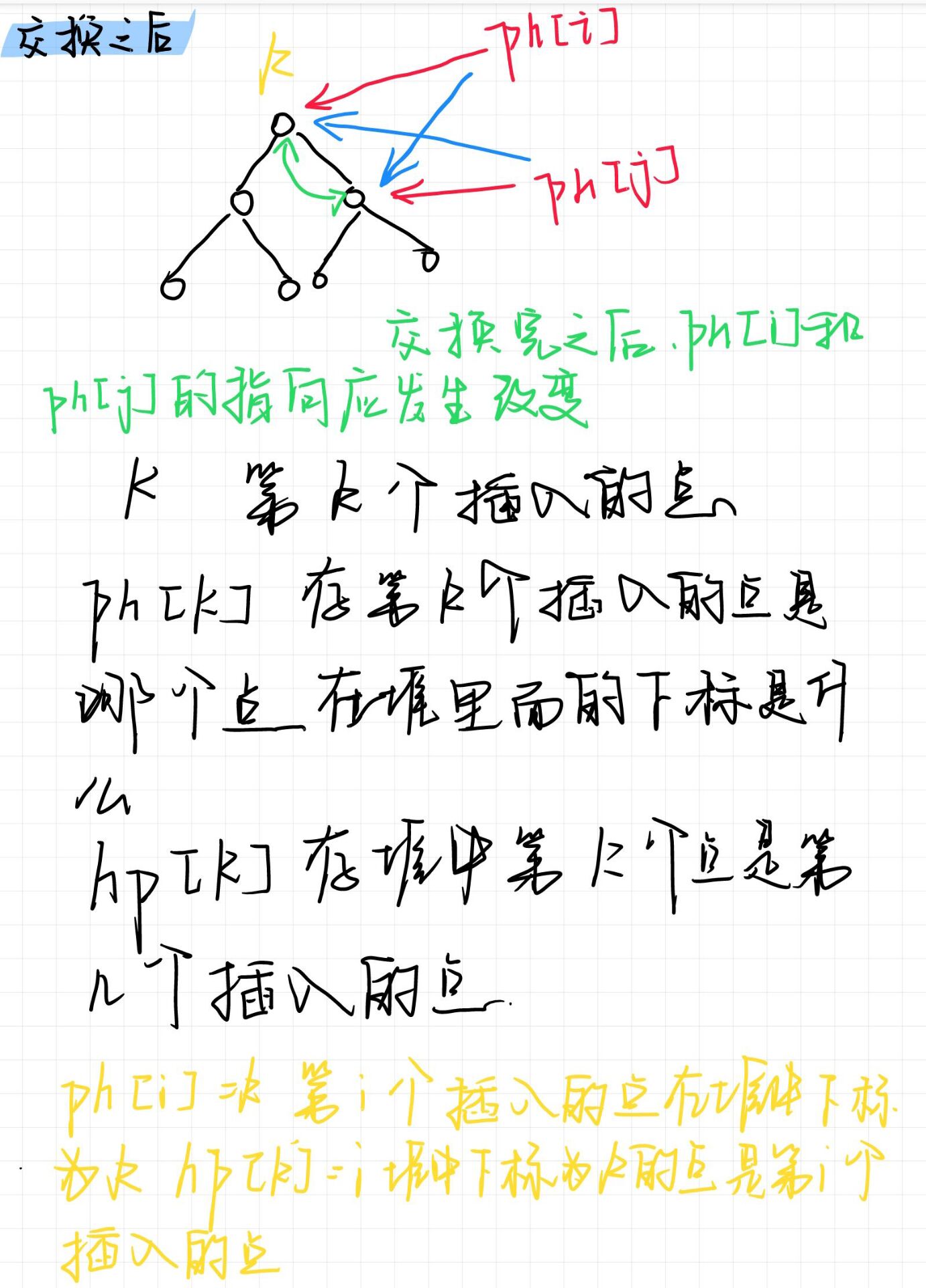
数据结构 堆
手写堆,而非stl中的堆 如何手写一个堆? //将数组建成堆 <O(n) for (int i n / 2;i;i--) //从n/2开始down down(i); 从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层…...
将 ONLYOFFICE 文档编辑器与 Node.js 应用集成
我们来了解下,如何将 ONLYOFFICE 文档编辑器与您的 Web 应用集成。 许多 Web 应用都可以从文档编辑功能中获益。但是要从头开始创建这个功能,需要花费大量时间和精力。幸运的是,您可以使用 ONLYOFFICE——这是一款开源办公套件,可…...
CentOS 7搭建Gitlab流程
目录 1、查询docker镜像gitlab-ce 2、拉取镜像 3、查询已下载的镜像 4、新建gitlab文件夹 5、在gitlab文件夹下新建相关文件夹 6、创建运行gitlab的容器 7、查看docker容器 8、根据Linux地址访问gitlab 9、进入docker容器,设置用户名的和密码 10、登录git…...
Idea安装完成配置
目录: 环境配置Java配置Maven配置Git配置 基础设置编码级设置File Header自动生成序列化编号配置 插件安装MyBtisPlusRestfulTooklkit-fix 环境配置 Java配置 Idea右上方,找到Project Settings. 有些版本直接有,有些是在设置下的二级菜单下…...

超详细~25考研规划~感恩现在努力的你!!!
25考研规划 俄语,翻译过来叫我爱你 考试时间 第一天 8.30-11.30政治——100分 2.00-5.00英语——100分 第二天 8.30-11.30数学——150分 2.00-5.00专业课——150分 1.什么是25考研 将在2024年12月参加考研,2025年本科毕业,9月读研究…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
