Semi-Supervised Multi-Modal Learning with Balanced Spectral Decomposition
相关文章：
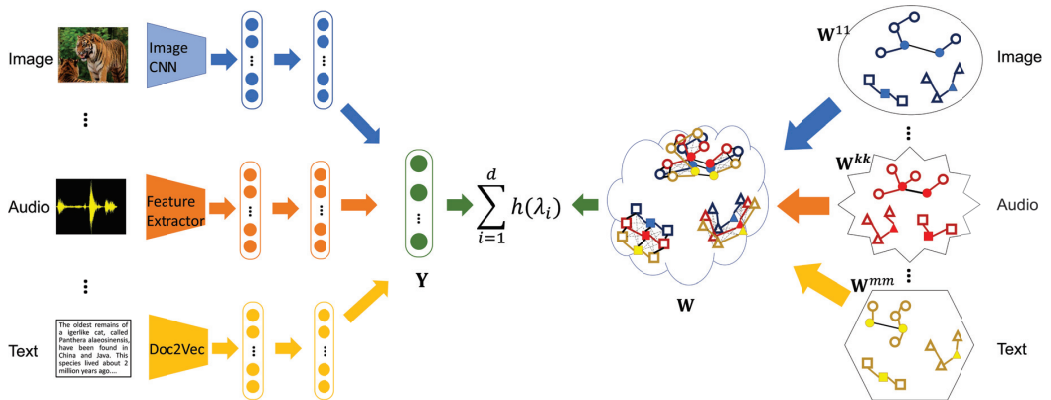
Semi-Supervised Multi-Modal Learning with Balanced Spectral Decomposition
Y是所有模态的表征矩阵， ∑ i 1 d h ( λ i ) \sum_{i1}^dh(\lambda_i) ∑i1dh(λi) is the proposed eigenvalue-based objective function,the final similarity matrix W for the multimodal data as a block matrix 辅助信息 作者未提供代码...
3296：【例50.2】 计算书费《信息学奥赛一本通编程启蒙（C++版）》
3296：【例50.2】 计算书费《信息学奥赛一本通编程启蒙（C版）》 【题目描述】 下面是一个图书的单价表： 1、计算概论 28.9 元/本 2、数据结构与算法 32.7 元/本 3、数字逻辑 45.6 元/本 4、C程序设计教程 78 元/本 5、人工智能…...
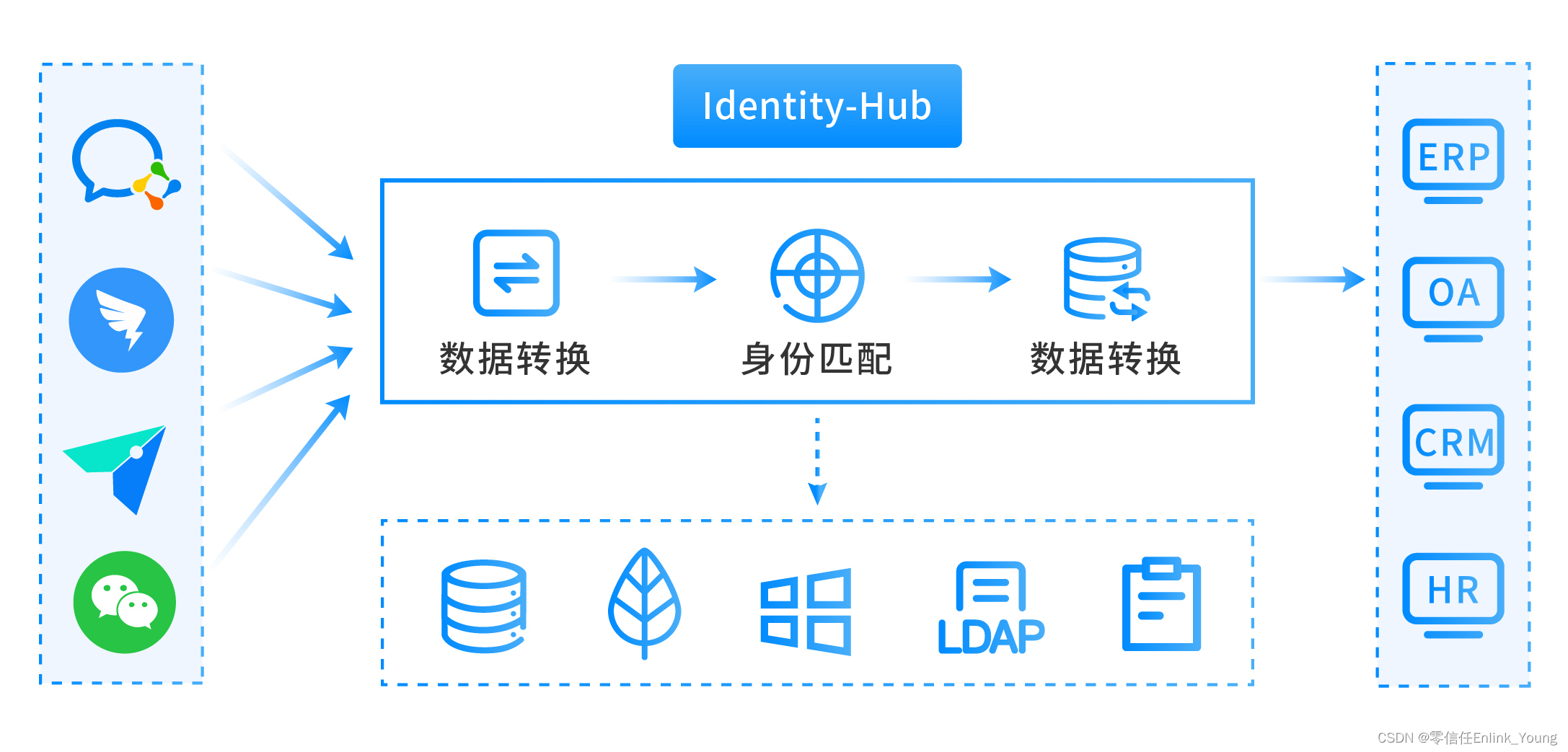
统一身份认证平台之SSO建设
前言 上篇说道Passwordless无密码技术，也提到了数字时代密码管理的难度，其实在日常的生活中，很多用户也会因为忘记某些网站的登录密码而烦恼。为了方便记忆，很多人都在不同的站点使用相同的用户名和密码，虽然也可以减少…...
【开题报告】基于SpringBoot的膳食营养健康网站的设计与实现
1.选题背景与意义 基于SpringBoot的膳食营养健康网站的设计与实现是一个具有重要意义的选题。背景和意义主要包括以下几点： （1）社会健康意识的提升：随着人们健康意识的提高，越来越多的人开始关注自己的饮食营养问题。…...
超五类网线和六类网线的相同点和区别
本文对超五类网线和六类网线的相同点和区别进行了简单介绍，帮助大家区分和建立相应的概念。 相同点： （1）都是网络跳线，用于连接网络设备。 （2）网线内部由8根不同颜色的线组成。 区别…...
Linux--初识和基本的指令（1）
目录 前言 0.什么是操作系统 0.1 搭建 Linux 环境 0.2搭建 Linux 环境小结 1.使用 XShell 远程登录 Linux 1.1关于 Linux 桌面 1.2下载安装 XShell 1.3查看 Linux 主机 ip 1.4XShell 下的复制粘贴 2.Linux下基本指令 2.1 pwd命令 2.2 ls命令 2.3 mkdir指令 2.4 cd…...
万宾科技智能井盖传感器，提升市政井盖健康
市政井盖就是城市里不可或缺的基础设施之一，关于它的监测工作可马虎不得。它承载着保护市民的交通安全以及城市正常运转的重要使命。虽然现在城市化的速度很快，但是传统的市政井盖管理方式变得有些力不从心了。井盖的覆盖范围很广，如果单单依…...
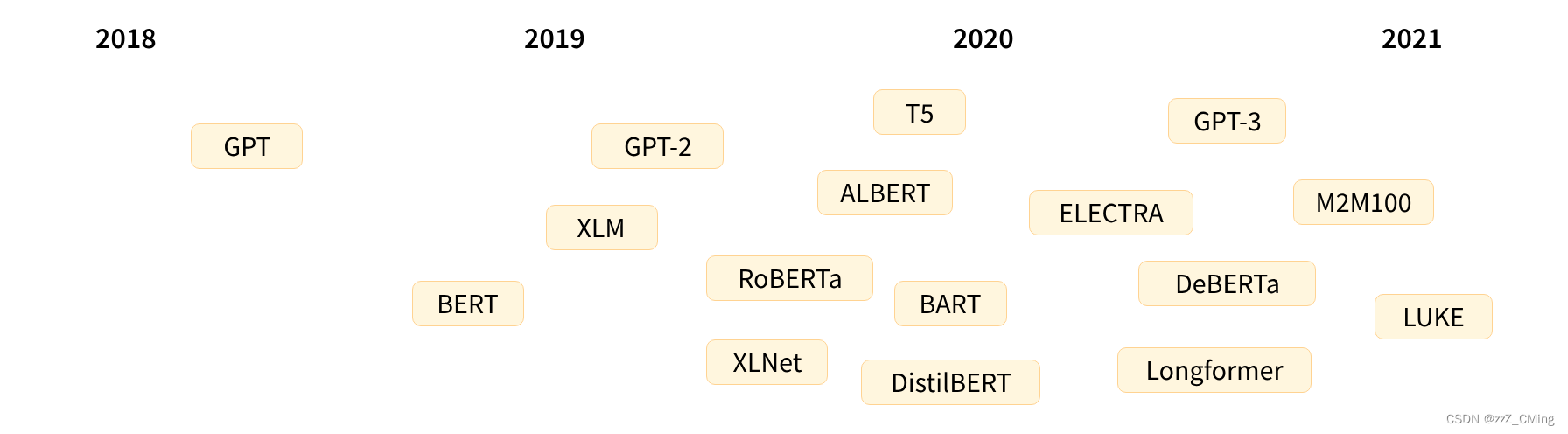
transformer学习资料
一、NLP 自然语言处理 NLP 是机器学习在语言学领域的研究，专注于理解与人类语言相关的一切。NLP 的目标不仅是要理解每个单独的单词含义，而且也要理解这些单词与之相关联的上下文之间的意思。 常见的NLP 任务列表： 对整句的分类࿱…...
一起学docker系列之四docker的常用命令--系统操作docker命令及镜像命令
目录 前言1 操作 Docker 的命令1.1 启动 Docker1.2 停止 Docker1.3 重启 Docker1.4 查看 Docker 状态1.5 查看 Docker 所有命令的信息1.6 查看某个命令的帮助信息 2 操作镜像的命令2.1 查看所有镜像2.2 搜索某个镜像2.3 下载某个镜像2.4 查看镜像所占空间2.5 删除镜像2.6 强制删…...
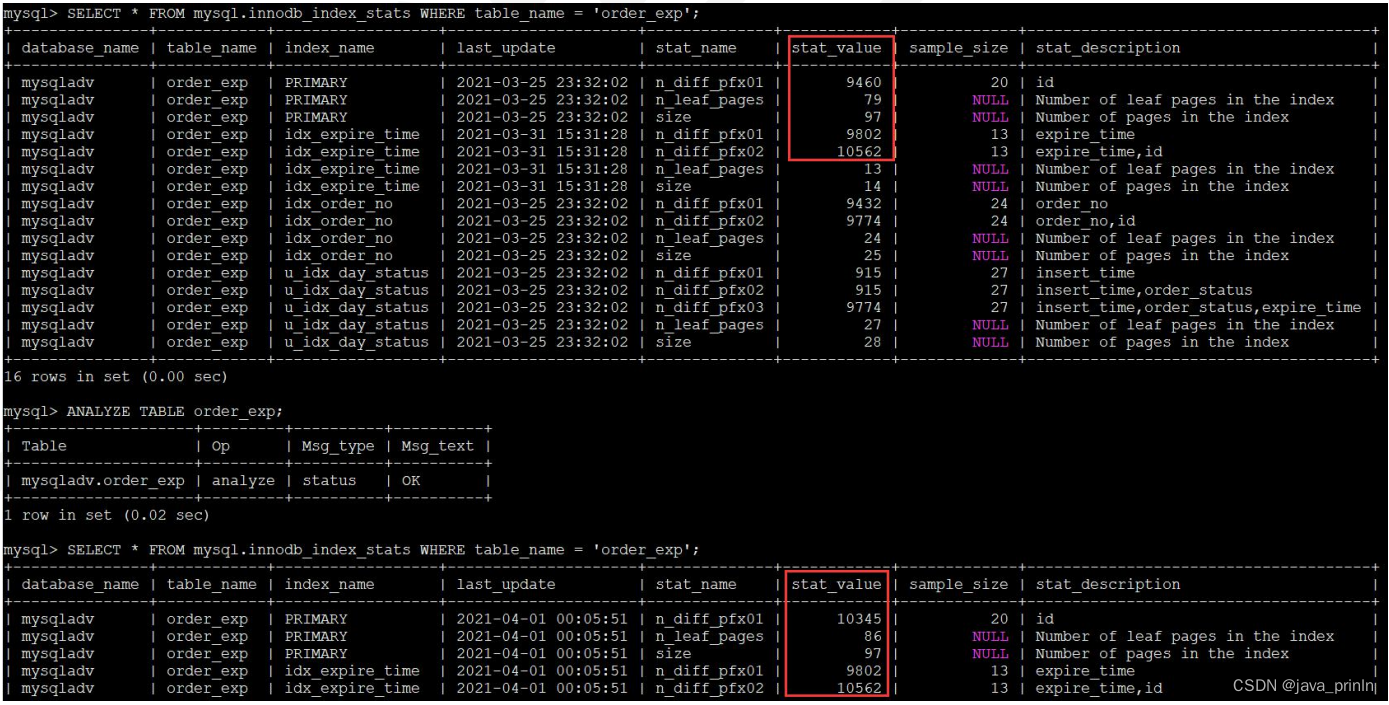
MySQL 的执行原理（三）
5.4. InnoDB 中的统计数据 我们前边唠叨查询成本的时候经常用到一些统计数据，比如通过 SHOW TABLE STATUS 可以看到关于表的统计数据，通过 SHOW INDEX 可以看到关于索引 的统计数据，那么这些统计数据是怎么来的呢？它们是以什么方…...
一道好题——分治
一道好题应该有一个简洁的题面。 有一个长度为 n，初始全为 0 的序列 a，另有一个长度为 n 的序列 b，你希望将 a 变成 b，你可以执行如下两种操作： 1 x：将 a 中所有值为 x 的数 11。 2 x：将 a 中下…...
庖丁解牛：NIO核心概念与机制详解 02 _ 缓冲区的细节实现
文章目录 PreOverview状态变量概述PositionLimitCapacity演示： 观察变量 访问方法get() 方法put()方法类型化的 get() 和 put() 方法 缓冲区的使用：一个内部循环 Pre 庖丁解牛：NIO核心概念与机制详解 01 接下来我们来看下缓冲区内部细节 Ov…...
 函数用法)
Python itertools模块中的combinations() 函数用法
Python itertools模块中的combinations 函数用法 调用方法示例1示例2 调用方法 itertools.combinations(iterable, r)各个参数意义： iterable：输入数据，数据应该是可迭代的。 r：子序列的长度 返回值：从输入的可迭代数…...
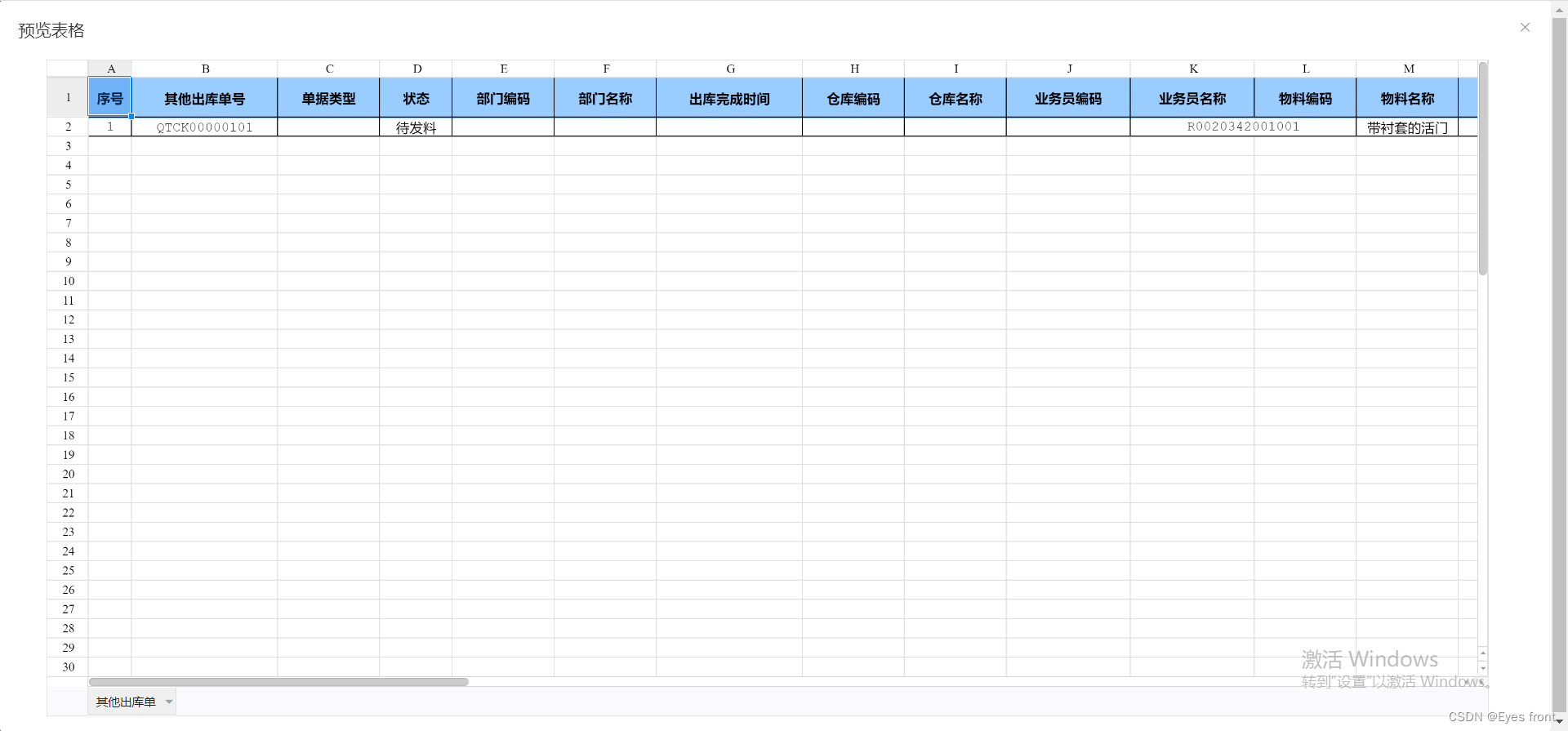
在线预览excel，luckysheet在vue项目中的使用
一. 需求 需要在内网项目中在线预览excel文档，并可以下载 二.在项目中下载并引入luckysheet 1.打开项目根目录，npm i luckyexcel 安装 npm i luckyexcel2.在项目的index.html文件中引入依赖 外网项目中的引入（CDN引入）&#…...
【python】OpenCV—Image Pyramid（8）
文章目录 1 图像金字塔2 拉普拉斯金字塔 1 图像金字塔 高斯金字塔 在 OpenCV 中使用函数 cv2.pyrDown()，实现图像高斯金字塔操作中的向下采样，使用函数 cv2.pyrUp() 实现图像金字塔操作中的向上采样 import cv2img cv2.imread(C://Users/Administrat…...
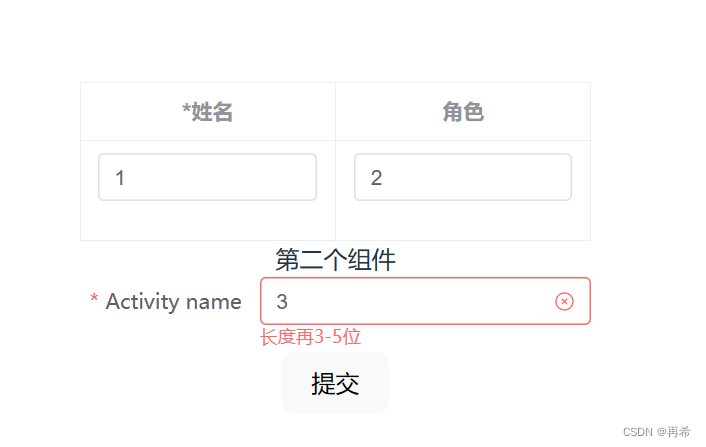
vue3父组件提交校验多个子组件
实现功能：在父组件提交事件中校验多个子组件中的form 父组件： <script setup lang"ts">import {ref, reactive} from vueimport childForm from ./childForm.vueimport childForm2 from ./childForm2.vuelet approvalRef ref()let ap…...
系统移植-uboot
uboot概述： 操作系统运行之前运行的一小段代码，用于将软硬件环境初始化到 一个合适的状态，为操作系统的加载和运行做准备（其本身不是操作系统） Bootloader基本功能 1.初始化软硬件环境 2.引导加载linux内核 3. 给lin…...
使用FFmpeg合并多个ts视频文件转为mp4格式
前言 爬取完视频发现都是ts文件，而且都是几百KB的视频片段，.ts 全名叫：MPEG Transport Stream，它是一个万能的多媒体容器，可以装下音频、视频、字幕。有时我们需要将.ts文件转换为其他更加广泛被支持的格式࿰…...
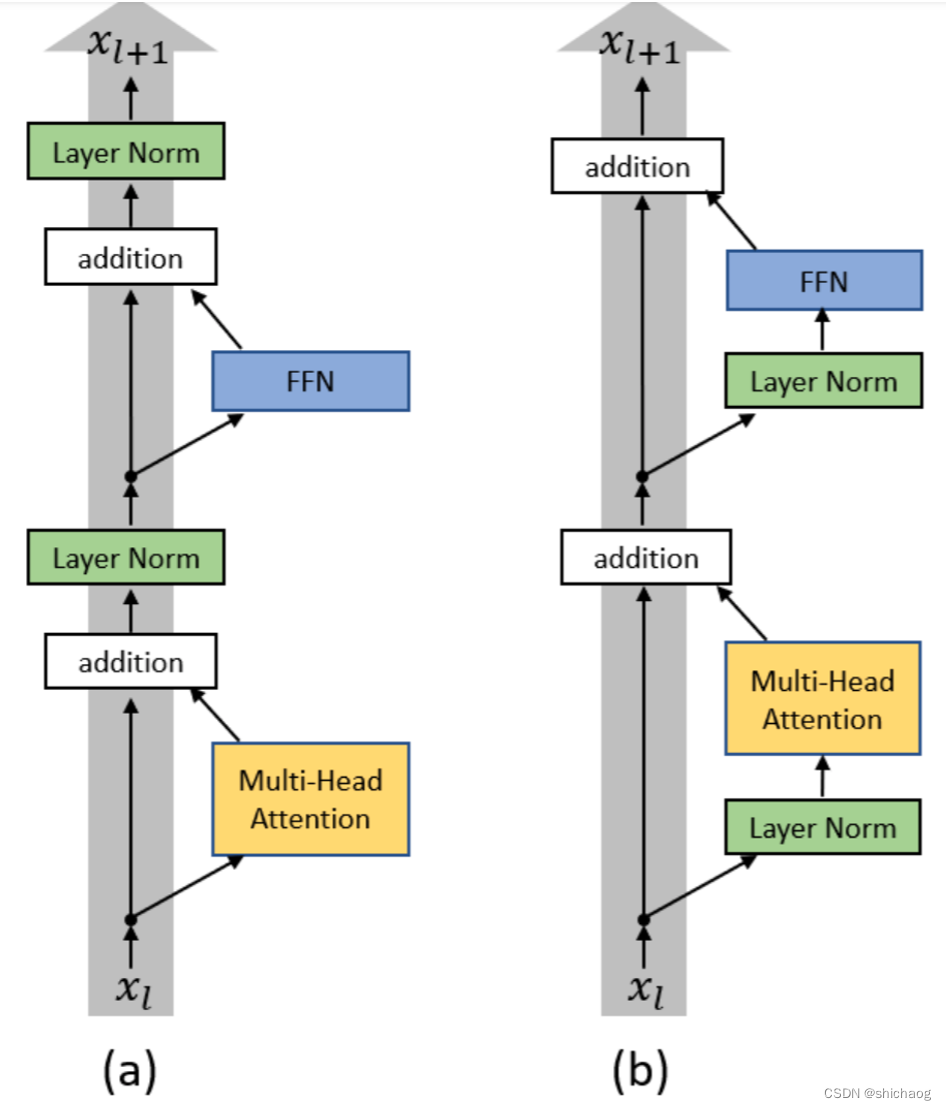
大模型之十二十-中英双语开源大语言模型选型
从ChatGPT火爆出圈到现在纷纷开源的大语言模型，众多出入门的学习者以及跃跃欲试的公司不得不面临的是开源大语言模型的选型问题。 基于开源商业许可的开源大语言模型可以极大的节省成本和加速业务迭代。 当前（2023年11月17日)开源的大语言模型如下&#…...
.Net6 部署到IIS示例
基于FastEndpoints.Net6 框架部署到IIS 环境下载与安装IIS启用与配置访问网站 环境下载与安装 首先下载环境安装程序，如下图所示,根据系统位数选择x86或者x64进行下载安装,网址：Download .NET 6.0。 IIS启用与配置 启用IIS服务 打开控制面板ÿ…...
aardio 简单网页自动化
WebView自动化，以前每次重复做网页登录、搜索这些操作时都觉得好麻烦，现在终于能让程序替我干活了，赶紧记录下这个超实用的技能！ 一、初次接触WebView WebView自动化就像给程序装了个"网页浏览器"，第一步得…...
DeepSeek 终章：破局之路，未来已来
目录 一、DeepSeek 技术发展现状回顾二、未来发展趋势2.1 多模态融合的拓展2.2 模型可解释性的强化2.3 垂直领域的深化应用 三、面临的技术挑战3.1 数据隐私与安全难题3.2 算法偏见与公平性困境3.3 网络攻击与恶意利用威胁 四、挑战应对策略探讨4.1 技术层面的解决方案4.2 算法…...
机器学习14-迁移学习
迁移学习学习笔记 一、迁移学习概述 迁移学习是机器学习中的一个重要领域，它旨在解决当目标任务的训练数据有限时，如何利用与目标任务相关但不完全相同的源任务数据来提高学习性能的问题。在现实世界中，获取大量高质量的标注数据往往成本高…...
pytorch 与 张量的处理
系列文章目录 文章目录 系列文章目录一、Tensor 的裁剪二、Tensor 的索引与数据筛选torch.wheretorch.indicestorch.gathertorch.masked_selecttorch.taketorch.nonzero（省略） 三、Tensor 的组合与拼接torch.cattorch.stack 四、Tensor的切片chunksplit …...
基于深度学习（Unet和SwinUnet）的医学图像分割系统设计与实现：超声心脏分割
基于深度学习的医学图像分割系统设计与实现 摘要 本文提出了一种基于深度学习的医学图像分割系统，该系统采用U-Net和Swin-Unet作为核心网络架构，实现了高效的医学图像分割功能。系统包含完整的训练、验证和推理流程，并提供了用户友好的图形界面。实验结果表明，该系统在医…...
Hadolint：Dockerfile 语法检查与最佳实践验证的终极工具
在容器化应用开发的浪潮中，Dockerfile 作为构建 Docker 镜像的核心配置文件，其质量直接影响着应用的安全性、稳定性和可维护性。然而，随着项目复杂度的增加，手动检查 Dockerfile 不仅耗时，还容易遗漏潜在问题。今天，我要向大家介绍一款强大的工具——Hadolint，它将彻底改…...
Vue解决开发环境 Ajax 跨域问题
一、前言 在使用 Vue 进行前后端分离开发时，前端通常运行在本地开发服务器（如 http://localhost:8080），而后端接口可能部署在其他域名或端口下（如 http://api.example.com:3000）。这时就可能出现 跨域&…...
性能优化笔记
性能优化转载 https://www.cnblogs.com/tengzijian/p/17858112.html 性能优化的一般策略及方法 简言之，非必要，不优化。先保证良好的设计，编写易于理解和修改的整洁代码。如果现有的代码很糟糕，先清理重构，然后再考…...
家政小程序开发——AI+IoT技术融合，打造“智慧家政”新物种
基于用户历史订单（如“每周一次保洁”）、设备状态（如智能门锁记录的清洁频率），自动生成服务计划。 结合天气数据（如“雨天推荐玻璃清洁”），动态推送服务套餐。 IoT设备联动&#x…...
rk3588 区分两个相同的usb相机
有时候会插入两个一模一样的usb相机，担心每次启动他们所对应的设备节点 /dev/video* 会变化，所以需要绑定usb口，区分两个相机。把两个相机都插入后，查看usb信息 rootrk3588:/# udevadm info --attribute-walk --name/dev/video0U…...