【机器学习Python实战】线性回归
🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习python实战 欢迎订阅!后面的内容会越来越有意思~
⭐内容说明:本专栏主要针对机器学习专栏的基础内容进行python的实现,部分基础知识不再讲解,有需要的可以点击专栏自取~
💡往期推荐(机器学习基础专栏):
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
【机器学习基础】多元线性回归(适合初学者的保姆级文章)
⭐本期内容:针对以上的一元和多元线性回归的梯度下降求解方法,进行代码展示
文章目录
- 一元线性回归
- 多元线性回归
一元线性回归
- 设计思路:
首先,class LinearRegression(object):定义一个LinearRegression类,继承自object类。
在这个类中,首先def __init__(self):定义类的构造函数。
在构造函数中,初始化线性回归模型的参数self.__M、self.__theta0和self.__theta1,以及梯度下降中的步长(学习率)self.__alpha。

线性回归模型是要不断计算输出的,所以定义函数def predict(self, x),用于预测给定输入x对应的输出。
同时线性回归的目的是通过迭代,不断的修改参数 θ \theta θ,所以需要定义函数用来做这个工作,它是通过梯度下降的方法来求解的,所以def __cost_theta0(self, X, Y)和def __cost_theta1(self, X, Y)这两个方法用于计算代价函数关于参数 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1的偏导数。
下面,def train(self, features, target)把上面的每个步骤和到了一起,定义了一个训练方法train,用于通过梯度下降算法找到最优的模型参数 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1的,使得代价函数的平方误差最小。在训练过程中,通过迭代更新参数,并输出每次迭代后的参数值。
在while的每一次迭代中,通过更新参数self.__theta0和self.__theta1来逐渐最小化代价函数的平方误差。
if "0:o.5f".format(prevt0) == "0:o.5f".format(self.__theta0) and "0:o.5f".format(prevt1) == "0:o.5f".format(self.__theta1):判断是否达到收敛条件,即两次迭代的参数值没有改变,如果满足条件,则退出循环。
最后,输出最终得到的参数值。

- 总体代码实现:
定义LinearRegression的class
#!/usr/bin/env python3
# 这是一个Shebang,指定了此脚本要使用的解释器为python3。
import numpyclass LinearRegression(object):# Constructor. Initailize Constants.def __init__(self):super(LinearRegression, self).__init__()self.__M = 0self.__theta0 = 2self.__theta1 = 2# defining Alpha I.E length of steps in gradient descent Or learning Rate.self.__alpha = 0.01def predict(self,x):return (self.__theta0 + x * self.__theta1)# Cost Function fot theta0.def __cost_theta0(self,X,Y):sqrerror = 0.0for i in range(0,X.__len__()):sqrerror += (self.predict(X[i]) - Y[i])return (1/self.__M * sqrerror)# Cost Function fot theta1.def __cost_theta1(self,X,Y):sqrerror = 0.0for i in range(0,X.__len__()):sqrerror += (self.predict(X[i]) - Y[i]) * X[i]return (1/self.__M * sqrerror)# training Data :# Finding Best __theta0 and __theta1 for data such that the Squared Error is Minimized.def train(self,features,target):# Validate Dataif not features.__len__() == target.__len__():raise Exception("features and target should be of same length")# Initailize M with Size of X and Yself.__M = features.__len__()# gradient descentprevt0, prevt1 = self.__theta0 , self.__theta1while True:tmp0 = self.__theta0 - self.__alpha * (self.__cost_theta0(features,target))tmp1 = self.__theta1 - self.__alpha * (self.__cost_theta1(features,target))self.__theta0, self.__theta1 = tmp0, tmp1print("theta0(b) :", self.__theta0)print("theta1(m) :", self.__theta1)if "0:o.5f".format(prevt0) == "0:o.5f".format(self.__theta0) and "0:o.5f".format(prevt1) == "0:o.5f".format(self.__theta1):breakprevt0, prevt1 = self.__theta0 , self.__theta1# Training Completed.# log __theta0 __theta1print("theta0(b) :", self.__theta0)print("theta1(m) :", self.__theta1)样例测试
from LinearRegression_OneVariables import LinearRegression
import numpy as npX = np.array([1,2,3,4,5,6,7,8,9,10])# Y = 0 + 1X
Y = np.array([1,2,3,4,5,6,7,8,9,10])modal = LinearRegression.LinearRegression()modal.train(X,Y)print(modal.predict(14))多元线性回归
- 设计思路:
首先,将文件导入,打乱顺序并选择训练集。
data=pd.read_csv("c:\\windquality.csv")data_array=data.values#shuffling for train test spplit
np.random.shuffle(data_array)train,test=data_array[:1200,:],data_array[1200:,:]
x_train=train[:,:-1]
x_test=test[:,:-1]
y_train=train[:,-1]
y_test=test[:,-1]

然后初始化参数,注意这里是多元的,所以有多个参数需要初始化。包括迭代次数和学习率
coef1=0
coef2=0
coef3=0
coef4=0
coef5=0
coef6=0
coef7=0
coef8=0
coef9=0
coef10=0
coef11=0
epoch=1000
alpha=.0001
然后使用梯度下降算法进行计算
总体代码实现:
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdata=pd.read_csv("c:\\windquality.csv")data_array=data.values#shuffling for train test spplit
np.random.shuffle(data_array)train,test=data_array[:1200,:],data_array[1200:,:]
x_train=train[:,:-1]
x_test=test[:,:-1]
y_train=train[:,-1]
y_test=test[:,-1]coef1=0
coef2=0
coef3=0
coef4=0
coef5=0
coef6=0
coef7=0
coef8=0
coef9=0
coef10=0
coef11=0
epoch=1000
alpha=.0001
c=0
n=len(y_train)
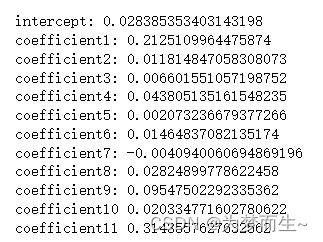
for i in range(epoch):y_pred=((coef1*x_train[:,0])+(coef2*x_train[:,1])+(coef3*x_train[:,2])+(coef4*x_train[:,3])+(coef5*x_train[:,4])+(coef6*x_train[:,5])+(coef7*x_train[:,6])+(coef8*x_train[:,7])+(coef9*x_train[:,8])+(coef10*x_train[:,9])+(coef11*x_train[:,10])+c)#to predict drivativeintercept=(-1/n)*sum(y_train-y_pred)dev1=(-1/n)*sum(x_train[:,0]*(y_train-y_pred))dev2=(-1/n)*sum(x_train[:,1]*(y_train-y_pred))dev3=(-1/n)*sum(x_train[:,2]*(y_train-y_pred))dev4=(-1/n)*sum(x_train[:,3]*(y_train-y_pred))dev5=(-1/n)*sum(x_train[:,4]*(y_train-y_pred))dev6=(-1/n)*sum(x_train[:,5]*(y_train-y_pred))dev7=(-1/n)*sum(x_train[:,6]*(y_train-y_pred))dev8=(-1/n)*sum(x_train[:,7]*(y_train-y_pred))dev9=(-1/n)*sum(x_train[:,8]*(y_train-y_pred))dev10=-1/n*sum(x_train[:,9]*(y_train-y_pred))dev11=-1/n*sum(x_train[:,10]*(y_train-y_pred))#linec=c-alpha*interceptcoef1=coef1-alpha*dev1coef2=coef2-alpha*dev2coef3=coef3-alpha*dev3coef4=coef4-alpha*dev4coef5=coef5-alpha*dev5coef6=coef6-alpha*dev6coef7=coef7-alpha*dev7coef8=coef8-alpha*dev8coef9=coef9-alpha*dev9coef10=coef10-alpha*dev10coef11=coef11-alpha*dev11print("\nintercept:",c,"\ncoefficient1:",coef1,"\ncoefficient2:",coef2,"\ncoefficient3:",coef3,"\ncoefficient4:",coef4,"\ncoefficient5:",coef5,"\ncoefficient6:",coef6,"\ncoefficient7:",coef7,"\ncoefficient8:",coef8,"\ncoefficient9:",coef9,"\ncoefficient10",coef10, "\ncoefficient11",coef11)#Calculating the predicted values
predicted_values = []
for i in range(0,399):y_pred = ((coef1 * x_test[i,0]) + (coef2 * x_test[i,1]) + (coef3 * x_test[i,2]) + (coef4 * x_test[i,3]) + (coef5 * x_test[i,4]) + (coef6 * x_test[i,5]) + (coef7 * x_test[i,6]) + (coef8 * x_test[i,7]) + (coef9 * x_test[i,8]) + (coef10 * x_test[i,9]) + (coef11 * x_test[i,10]) + intercept)predicted_values.append(y_pred)for i in range(len(predicted_values)):print(predicted_values[i])相关文章:

【机器学习Python实战】线性回归
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习python实战 欢迎订阅!后面的内容会越来越有意思~ ⭐内容说明:本专栏主要针对机器学习专栏的基础内容进行python的实现,部分…...

做外贸这么久,为什么一直做不好?
很多外贸业务员在开发客户过程中,总感觉自己做了很多事情,聊了很多客户,但却总是拿不到单子。 其实,这是由于缺乏对采购商心理的认识程度,没有换位思考,该做的事没做,不该做的事却忙得忘乎所以&…...
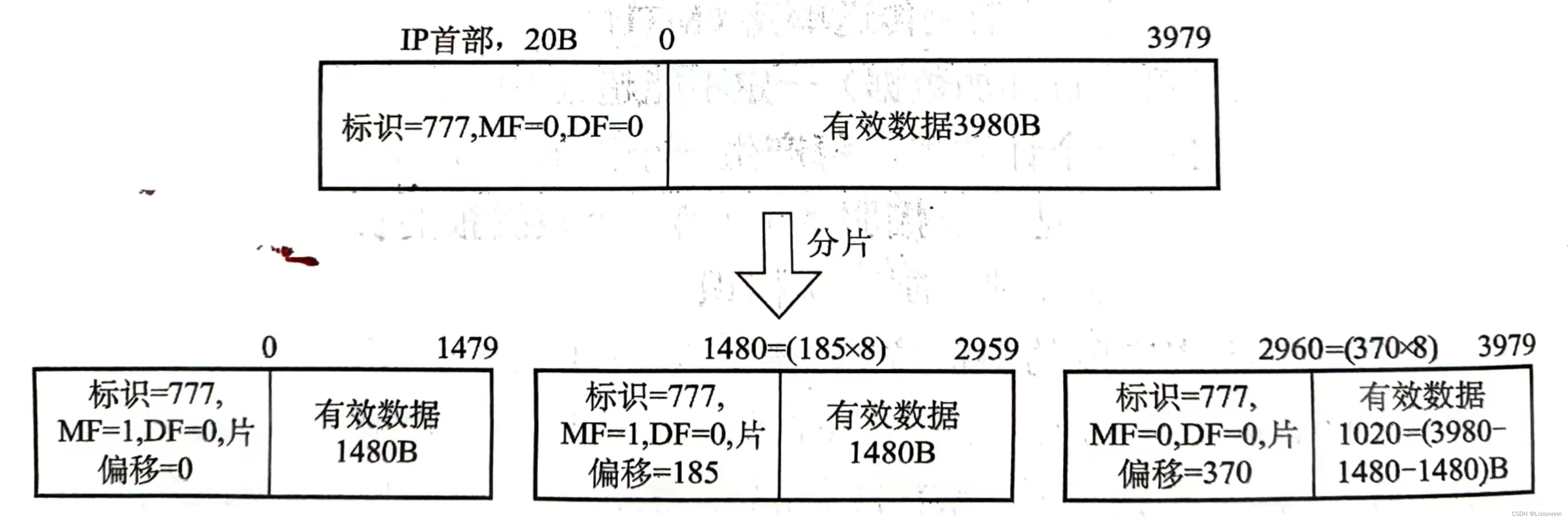
IPv4数据报格式
IPv4是IP协议的第四个版本(版本1-3和版本5都未曾使用过)IP地址不能反映任何有关主机位置的地理信息以前还有个逆地址解析协议RAPR(Reverse APR),它的作用是使只知道自己MAC地址的主机能通过RAPR找到其IP地址,而现在的DHCP(Dynamic Host Configuration Pr…...
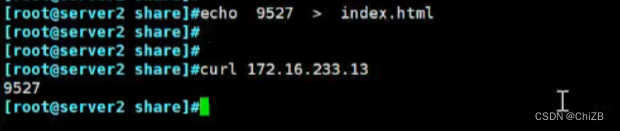
搭建网关服务器实现DHCP自动分配、HTTP服务和免密登录
目录 一. 实验要求 二. 实验准备 三. 实验过程 1. 网关服务器新建网卡并改为仅主机模式 2. 修改新建网卡IP配置文件并重启服务 3. 搭建网关服务器的dhcp服务 4. 修改server2网卡配置文件重启服务并效验 5. 设置主机1的网络连接为仅主机模式 6. 给server2和网关服务器之…...
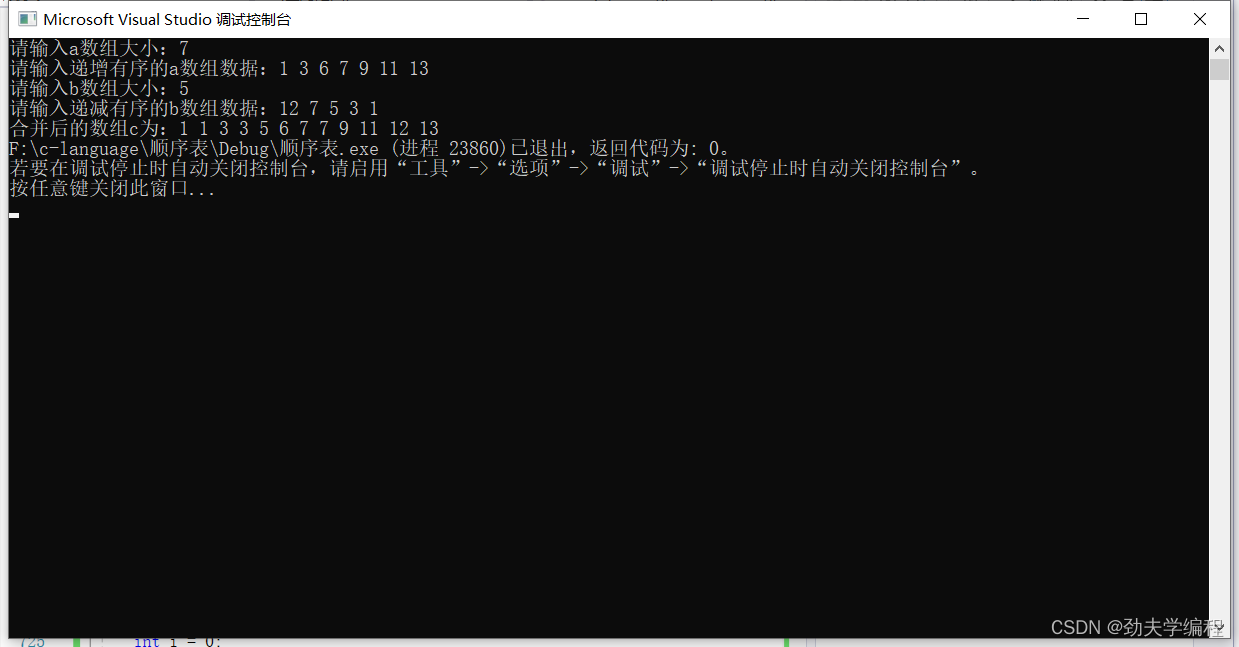
【18年扬大真题】给定有m个整数的递增有序数组a和有n个整数的递减有序数组b,将a数组和b数组归并为递增有序的数组c
【18年扬大真题】 给定有m个整数的递增有序数组a和有n个整数的递减有序数组b, 将a数组和b数组归并为递增有序的数组c。 void Merge(int arr[],int m ,int brr[],int n,int crr[]) {int i 0;int j n-1;int k 0;while(i < m&&j > 0) {if (arr[i] &l…...

图片叠加_图片压缩
图片叠加 try {/* 1 读取第一张图片*/File fileOne new File("1.png");BufferedImage imageFirst ImageIO.read(fileOne);/* 2读取第二张图片 */File fileTwo new File("2.png");BufferedImage imageSecond ImageIO.read(fileTwo);//创建一个最底层画…...
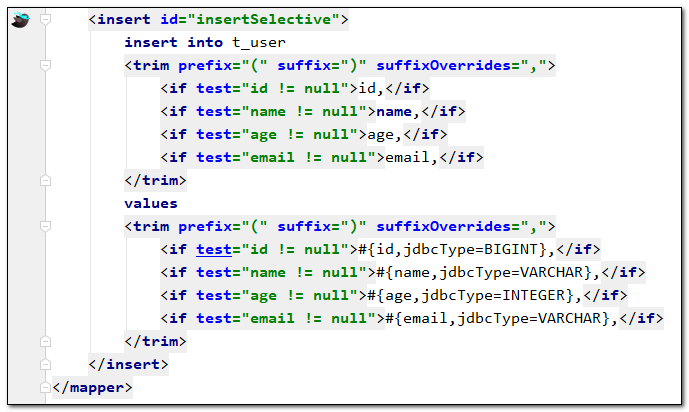
Mybatis-Plus《学习笔记 22版尚硅谷 》——感谢【尚硅谷】官方文档
Mybatis-Plus《学习笔记 22版尚硅谷 》 一、MyBatis-Plus1.简介2.特性3.支持数据库4.框架结构5.官方地址 二、入门案例1.开发环境2.建库建表3.创建工程4.配置编码5.测试查询 三、增删改查1.BaseMapper<T>2.调用Mapper层实现CRUD2.1 插入2.2 删除a、根据ID删除数据b、根据…...

git安装后报git: ‘remote-https‘ is not a git command. See ‘git --help‘.
1. 问题说明 使用的是linux系统,采用编译安装的方式进行安装,安装完成clone项目后提示“git: ‘remote-https’ is not a git command. See ‘git --help’.” 2. 问题解决 需要安装1个额外的库:libcurl4-openssl-de sudo apt-get install …...

场景交互与场景漫游-交运算与对象选取(8-1)
交运算与对象选取 在面对大规模的场景管理时,场景图形的交运算和图形对象的拾取变成了一项基本工作。OSG作为一个场景管理系统,自然也实现了场景图形的交运算,交运算主要封装在osgUtil 工具中在OSG中,osgUtil是一个非常强有力的工…...

Vue中动态Class实战
效果展示 需求 想实现一个假如有5个div块,默认都是灰色,鼠标悬浮到哪个div上,那个div就显示为黑色。 具体的实现业务逻辑可根据这个进行演变 设计 通过动态 class 类名来实现,实现鼠标悬浮到div时动态绑定class 版本 Vue 3.…...
B站短视频如何去水印?一键解析下载B站视频!
在浏览B站视频时,我们有时会遇到带有水印的场景。这些水印可能会干扰我们对视频内容的观看体验,特别是在全屏观看时。此外,当我们想要保存或分享这些视频时,水印也会成为一种障碍。因此,去除水印的需求就变得非常迫切。…...

最大子段和(分治法+动态规划法)
求最大子段和 此类问题通常是求数列中连续子段和的最大值,经典的股票问题就是考察的这个思想及拓展。 例题: AcWing:1054. 股票买卖 Leetcode:53. 最大子数组和 分治法O(nlogn) 此类问题时分适合采用分治思想,因为所有子区间 [ s t a r t …...
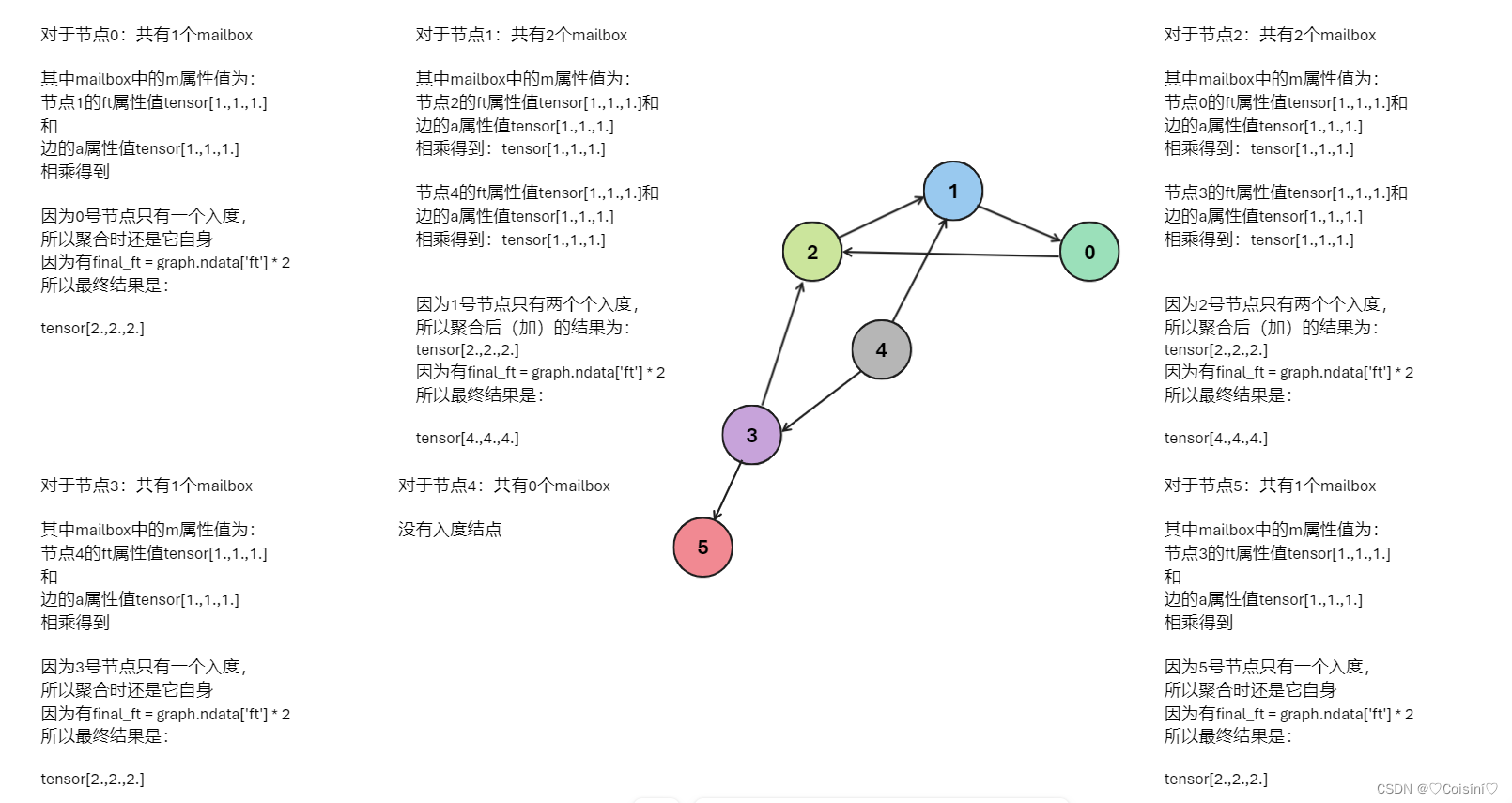
内置函数和消息传递API
消息传递范式 消息函数、聚合函数与更新函数 消息函数接受一个参数 edges,这是一个 EdgeBatch 的实例, 在消息传递时,它被DGL在内部生成以表示一批边。edges 有 src、 dst 和 data 共3个成员属性, 分别用于访问源节点、目标节点…...

不标年份的葡萄酒质量好吗?
我们在葡萄酒标上经常看到生产年份,也就是指全部葡萄采摘的年份。旧世界葡萄酒产国认为葡萄酒年份对他们的影响较大,而新世界葡萄酒,年份的意义就稍微小些。甚至有一部分葡萄酒酒标上没有年份。在酒标上没有标注年份的葡萄酒,被称…...
2023年【高处安装、维护、拆除】模拟考试题及高处安装、维护、拆除模拟考试题库
题库来源:安全生产模拟考试一点通公众号小程序 2023年【高处安装、维护、拆除】模拟考试题及高处安装、维护、拆除模拟考试题库,包含高处安装、维护、拆除模拟考试题答案和解析及高处安装、维护、拆除模拟考试题库练习。安全生产模拟考试一点通结合国家…...

简单模拟 Spring 创建的动态代理类(解释一种@Transactional事务失效的场景)
模拟 Spring 创建的动态代理类 本文主要目的是从父类和子类继承的角度去分析为什么在 Service 标注的业务类中使用 this 调用方法会造成事务失效。解释在这种情况下 this 为什么是原始类对象而不是代理类对象。 问题描述 在 Service 标注的业务类中,如果调用本类…...
万户OA upload任意文件上传漏洞复现
0x01 产品简介 万户OA ezoffice是万户网络协同办公产品多年来一直将主要精力致力于中高端市场的一款OA协同办公软件产品,统一的基础管理平台,实现用户数据统一管理、权限统一分配、身份统一认证。统一规划门户网站群和协同办公平台,将外网信息…...

如何写好一篇软文?怎样写软文比较有吸引力?
软文,即柔性广告,是一种通过文字、图片等形式,将广告信息融入到内容中,以达到宣传、推广、营销目的的文章。企业和品牌每天都会在互联网上投放大量软文,软文起到润物细无声的作用,可以在无形中影响用户心智…...

从0开始学习JavaScript--JavaScript中的对象
JavaScript中的对象是一种重要的数据结构,它不仅是语言的基石,还提供了丰富的功能和灵活性。本文将深入研究JavaScript对象的创建、属性访问、方法定义,以及实际应用中的技巧,通过丰富的示例代码,帮助读者更全面地了解…...
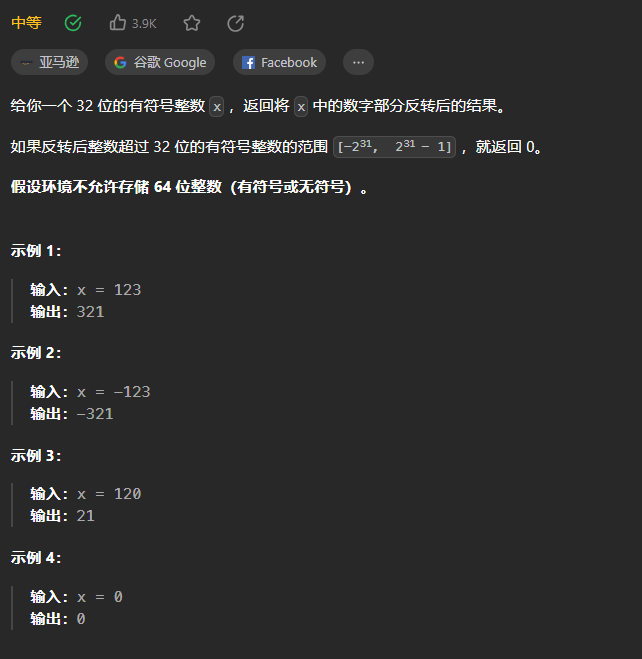
【LeetCode刷题】--7.整数反转
7.整数反转 注意:在推入数字之前,需要判断MIN_VALUE< res*10digit<MAX_VALUE,不满足就返回0 class Solution {public int reverse(int x) {int res 0;while(x!0){//需要判断MIN_VALUE< res*10digit<MAX_VALUEif(res < Integ…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
