常见的面试算法题:阶乘、回文、斐波那契数列
1.阶乘算法 Factorial
例如:给出数字5,对其以下的的每个数字相乘,结果等于120
解:递归 Recursive
function factorial(n) {// 如果n为0或1,阶乘是1if (n === 0 || n === 1) {return 1;}// 否则,返回n乘以n-1的阶乘return n * factorial(n - 1);
}
console.log(factorial(5)); // 输出 120
虽然递归是一个直观的解决方案,但对于非常大的数字,递归可能导致栈溢出错误。对于更大的数字,你可以使用迭代方法来避免栈溢出:
解:迭代 Iterative
function factorialIterative(n) {let result = 1;for (let i = 2; i <= n; i++) {result *= i;}return result;
}
console.log(factorialIterative(5)); // 输出 120
2.回文算法 Palindrome
实现一个检查回文的算法相对简单。回文是一个字符串,它从前往后读和从后往前读是一样的。下面是一个简单的实现:
解:使用系统自带的reverse函数
function isPalindrome(str) {// 移除非字母数字字符并转换为小写const cleanedStr = str.replace(/[\W_]/g, '').toLowerCase();// 检查清理后的字符串是否是回文return cleanedStr === cleanedStr.split('').reverse().join('');
}
// 使用示例
console.log(isPalindrome("A man, a plan, a canal, Panama")); // 应该输出 true
console.log(isPalindrome("racecar")); // 应该输出 true
console.log(isPalindrome("hello")); // 应该输出 false
解:不使用系统自带的reverse函数
这种方法不需要改变字符串本身,只需遍历到字符串的一半即可。
a.清理字符串:和之前一样,首先移除所有非字母数字的字符,并将所有字符转换为同一大小写。b.手动比较字符:遍历清理后的字符串,直到中间位置。在每一步中,比较第 i 个字符和倒数第 i 个字符。如果这些字符在任何时候不匹配,函数应该返回 false。如果所有对应的字符都匹配,则字符串是回文。
function isPalindrome(str) {const cleanedStr = str.replace(/[\W_]/g, '').toLowerCase();const len = cleanedStr.length;for (let i = 0; i < len / 2; i++) {if (cleanedStr[i] !== cleanedStr[len - 1 - i]) {return false;}}return true;
}
// 使用示例
console.log(isPalindrome("A man, a plan, a canal, Panama")); // 应该输出 true
console.log(isPalindrome("racecar")); // 应该输出 true
console.log(isPalindrome("hello")); // 应该输出 false
3.斐波那契数列算法 Fibonacci
斐波那契数列是一个著名的数列,其中每个数字是前两个数字之和。数列以0和1开始,后续的数是通过加前两个数来得到的。在JavaScript中实现斐波那契数列有几种方法,包括递归、动态规划和闭包。
1.递归
递归是最直观的实现方式,但对于较大的数字效率较低,因为它包含了大量的重复计算。
function fibonacciRecursion(n) {if (n < 2) {return n;}return fibonacciRecursion(n - 1) + fibonacciRecursion(n - 2);
}
2.动态规划
动态规划方法存储了中间结果,避免了重复计算,因此效率更高。
function fibonacciDynamic(n) {let fib = [0, 1];for (let i = 2; i <= n; i++) {fib[i] = fib[i - 1] + fib[i - 2];}return fib[n];
}
3.闭包
使用闭包可以创建一个函数,记住之前计算的值,从而避免重复计算。
function fibonacciClosure() {let cache = [0, 1];return function fib(n) {if (cache[n] !== undefined) {return cache[n];}cache[n] = fib(n - 1) + fib(n - 2);return cache[n];}
}
const fib = fibonacciClosure();
未完待续。。。
相关文章:

常见的面试算法题:阶乘、回文、斐波那契数列
1.阶乘算法 Factorial 例如:给出数字5,对其以下的的每个数字相乘,结果等于120 解:递归 Recursive function factorial(n) {// 如果n为0或1,阶乘是1if (n 0 || n 1) {return 1;}// 否则,返回n乘以n-1的…...

微服务 Spring Cloud 7,Nacos配置中心的Pull原理,附源码
目录 一、本地配置二、配置中心1、以Nacos为例:2、Pull模式3、也可以通过Nacos实现注册中心 三、配置中心提供了哪些功能四、如何操作配置中心1、配置注册2、配置反注册3、配置查看4、配置变更订阅 五、主流的微服务注册中心有哪些,如何选择?…...

c#Nettonsoft.net库常用的方法json序列化反序列化
Newtonsoft.Json 是一个流行的 JSON 操作库,用于在 .NET 应用程序中序列化、反序列化和操作 JSON 数据。下面是 Newtonsoft.Json 常用的一些方法: 序列化对象为 JSON 字符串: string json JsonConvert.SerializeObject(obj);var obj new {…...

力扣刷题-二叉树-二叉树的高度与深度
二叉树最大深度 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 递归法 本题可以使用前序(中左…...

Vue3新增加的css语法糖
一、deep <template><div class""><el-input /> </div> </template> <style scoped> /* 样式穿透 */ :deep input {background: red; } </style> 二、slotted 子组件修改插槽里面的样式 <template><div clas…...
Windows安装Vmware 虚拟机
目录 一、Vmware 虚拟机介绍 二、Vmware 虚拟机的三种网络模式 2.1桥接模式 2.2仅主机模式 2.3NAT 网络地址转换模式 三、Vmware 虚拟机的安装 一、Vmware 虚拟机介绍 VMware Workstation Pro 是一款可以在个人电脑的操作系统上创建一个完全与主机操作系统隔离的 虚拟机&…...

uniapp地图手动控制地图scale
前言 首次使用uniapp开发地图过程中,发现uniapp地图居然没有提供手动控制地图scale的方法,这个也着实没有想到,查了半天资料,也终于找到一个方法能够比较好的控制scale,做个记录。 代码 要定义一个地图mapÿ…...

Kotlin学习之函数
原文链接 Understanding Kotlin Functions 函数对于编程语言来说是极其重要的一个组成部分,函数可以视为是程序的执行,是真正活的代码,为啥呢?因为运行的时候你必须要执行一个函数,一般从主函数入口,开始一…...
若依启动步骤
1.创建数据库 2.启动redis 3.改后端的数据库连接配置 4.配置redis redis的地址:cmd中ipconfig命令查看 6.启动后端:如下 7.启动前端ruoyi-ui中 先运行npm install,再npm run dev。项目就启动成功了。 用户名:admin 密码&#x…...
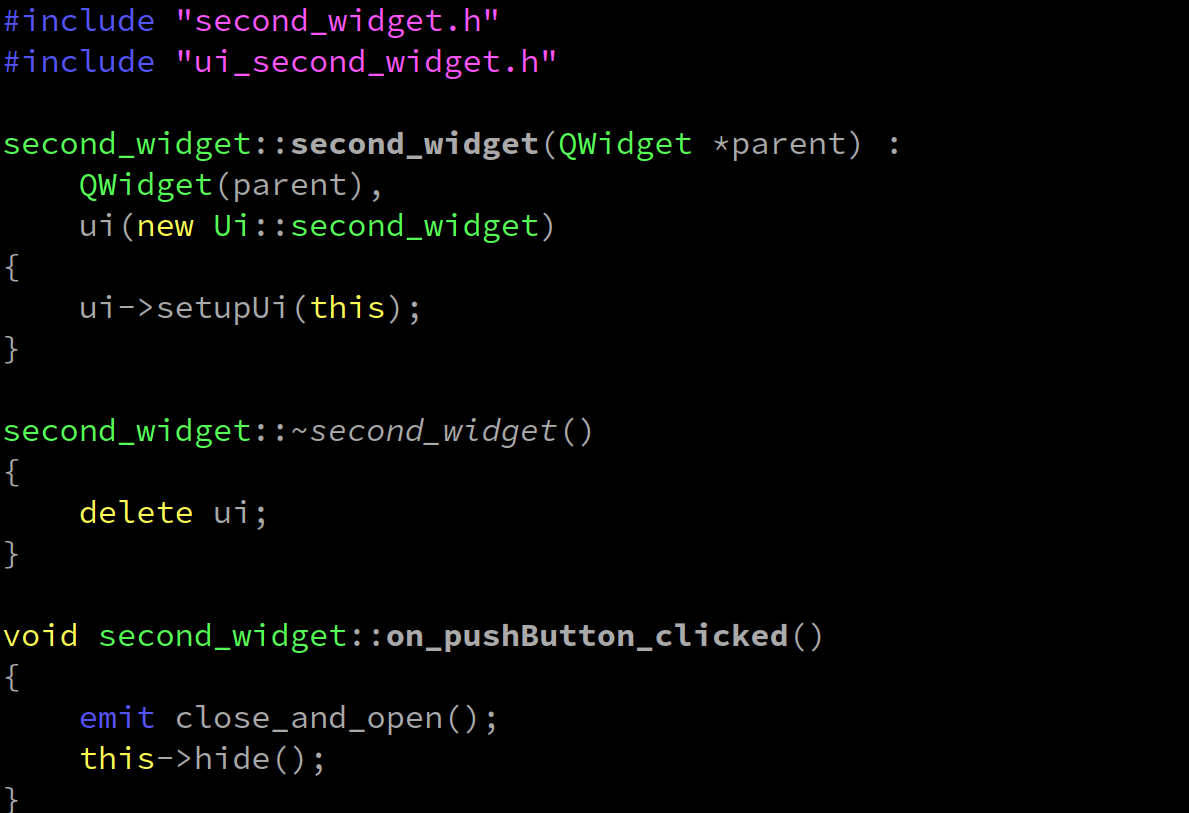
qt-C++笔记之两个窗口ui的交互
qt-C笔记之两个窗口ui的交互 code review! 文章目录 qt-C笔记之两个窗口ui的交互0.运行1.文件结构2.先创建widget项目,搞一个窗口ui出来3.项目添加第二个widget窗口出来4.补充代码4.1.qt_widget_interaction.pro4.2.main.cpp4.3.widget.h4.4.widget.cpp4.5.second…...
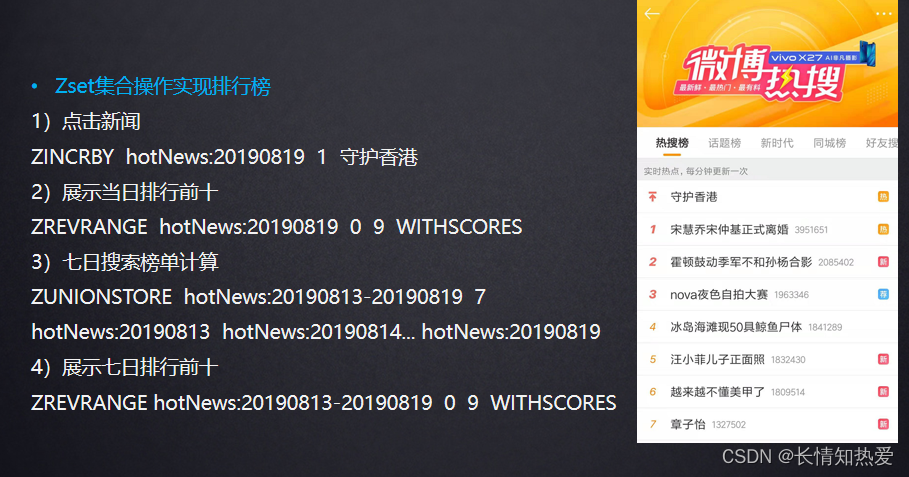
Redis-核心数据结构
五种数据结构 String结构 String结构应用场景 Hash结构 Hash结构应用场景 List结构 List结构应用场景 Set结构 Set结构应用场景 ZSet有序结构 ZSet有序结构应用场景...

设计模式—结构型模式之外观模式(门面模式)
设计模式—结构型模式之外观模式(门面模式) 外观(Facade)模式又叫作门面模式,是一种通过为多个复杂的子系统提供一个一致的接口,而使这些子系统更加容易被访问的模式。 例子 我们的电脑会有很多 组件&am…...

CentOS Stream 9-使用 systemd 管理自己程序时自定义日志路径
systemd 文件 [rootnode1 ~]# cat /etc/systemd/system/spms-wvp.service [Unit] DescriptionWVP service [Service] # 关键配置部分,注意这里的 spms-wvp ,后面需要用 SyslogIdentifierspms-wvp StandardOutputsyslog StandardErrorsyslog Typesimple Environment…...
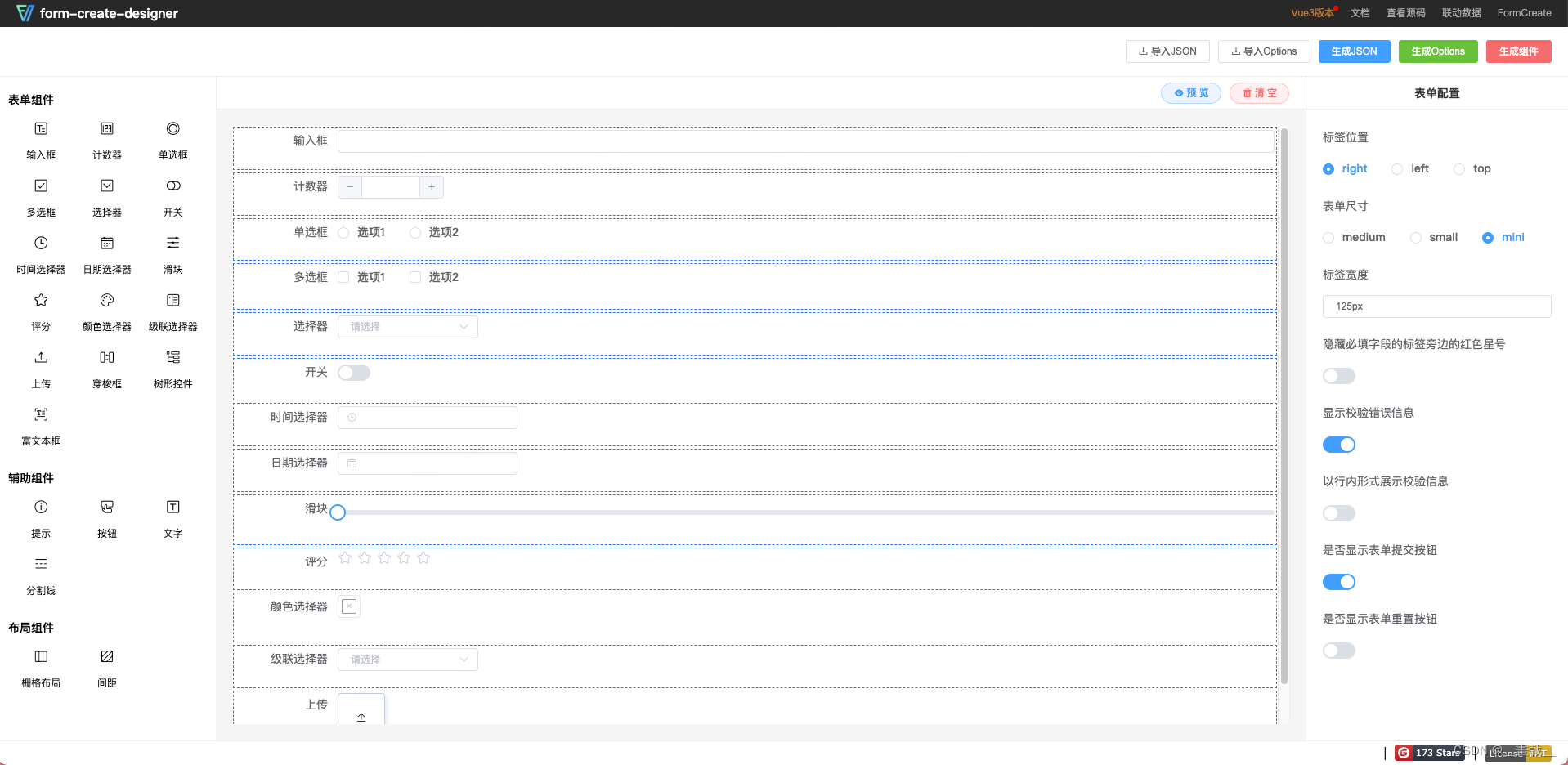
动态页面调研及设计方案
文章目录 vue2 动态表单、动态页面调研一、form-generator二、ng-form-element三、Variant Form四、form-create vue2 动态表单、动态页面调研 一、form-generator 预览:https://mrhj.gitee.io/form-generator/#/ Vue2 Element UI支持拖拽生成表单不支持其他组件…...
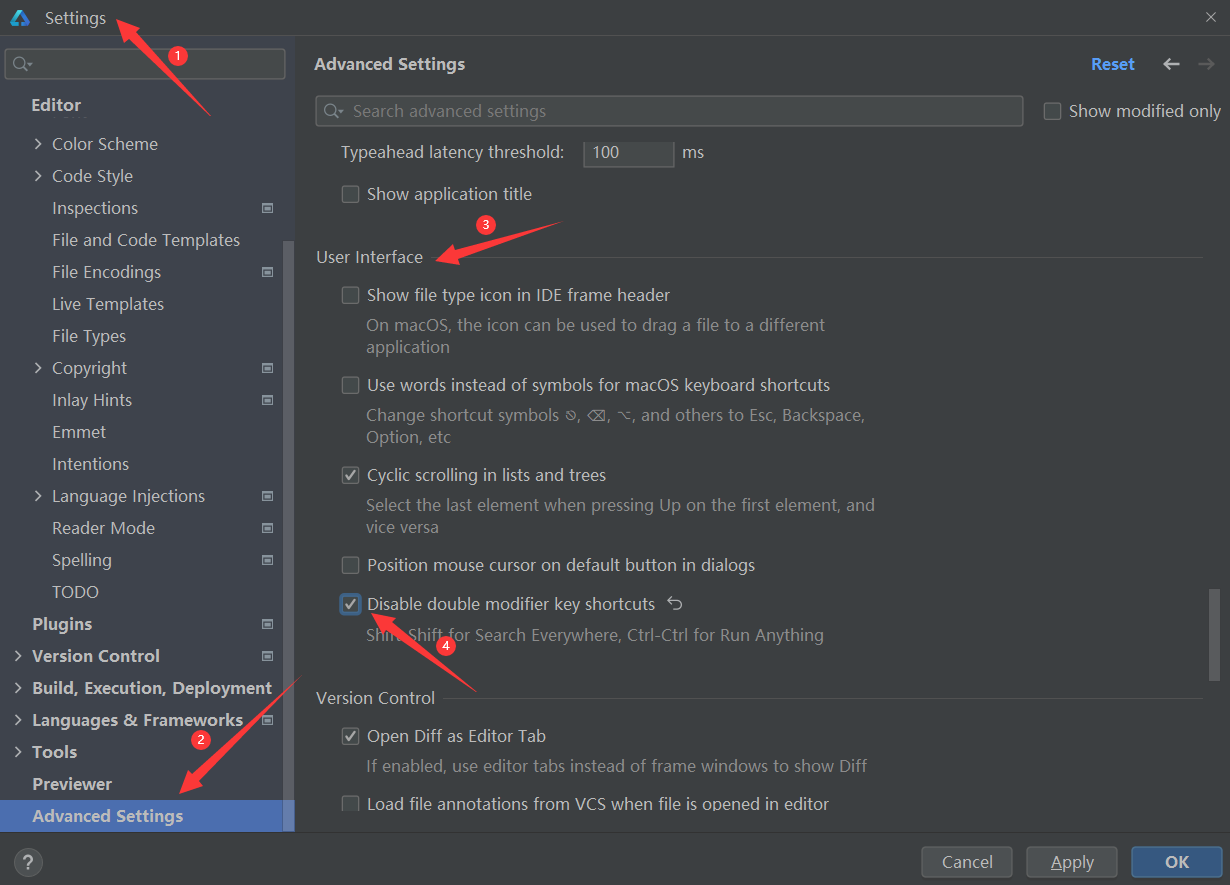
鸿蒙4.0开发笔记之DevEco Studio之配置代码片段快速生成(三)
一、作用 配置代码片段可以让我们在Deveco Studio中进行开发时快速调取常用的代码块、字符串或者某段具有特殊含义的文字。其实现方式类似于调用定义好变量,然而这个变量是存在于Deveco Studio中的,并不会占用项目的资源。 二、配置代码段的方法 1、打…...

HarmonyOS真机调试报错:INSTALL_PARSE_FAILED_USESDK_ERROR处理
文章目录 1、 新建应用时选择与自己真机匹配的sdk版本2、 根据报错提示连接打开处理方案3、查询真机版本对应的**compileSdkVersion** 和 **compatibleSdkVersion** 提示3.1版本之后和3.1版本之前的不同命令(此处为3.0版本)4、根据查询修改参数5、连接成…...

webSocket基于面向对象二次封装
今天不睡,熬夜赶了个WebSocket 二次封装,也对这几天文章摸鱼感到抱歉,所以我出了一个注释非常非常全的代码 思路如下 首先,需要通过调用connect方法来建立WebSocket连接。当连接成功时,会调用我提供的回调函数,并将连接成功的消息帧作为参数…...

【Web】PHP反序列化的一些trick
目录 ①__wakeup绕过 ②加号绕过正则匹配 ③引用绕过相等 ④16进制绕过关键词过滤 ⑤Exception绕过 ⑥字符串逃逸 要中期考试乐(悲) ①__wakeup绕过 反序列化字符串中表示属性数量的值 大于 大括号内实际属性的数量时,wakeup方法会被绕过 (php5-p…...

【测试功能篇 01】Jmeter 压测接口最大并发量、吞吐量、TPS
压力测试,我们针对比较关键的接口,可以进行相应的压力测试,主要还是测试看看接口能抗住多少的请求数,TPS稳定在多少,也就是吞吐量多少 安装 Jmeter的安装很简单,官网下载地址 http://jmeter.apache.org/ &…...
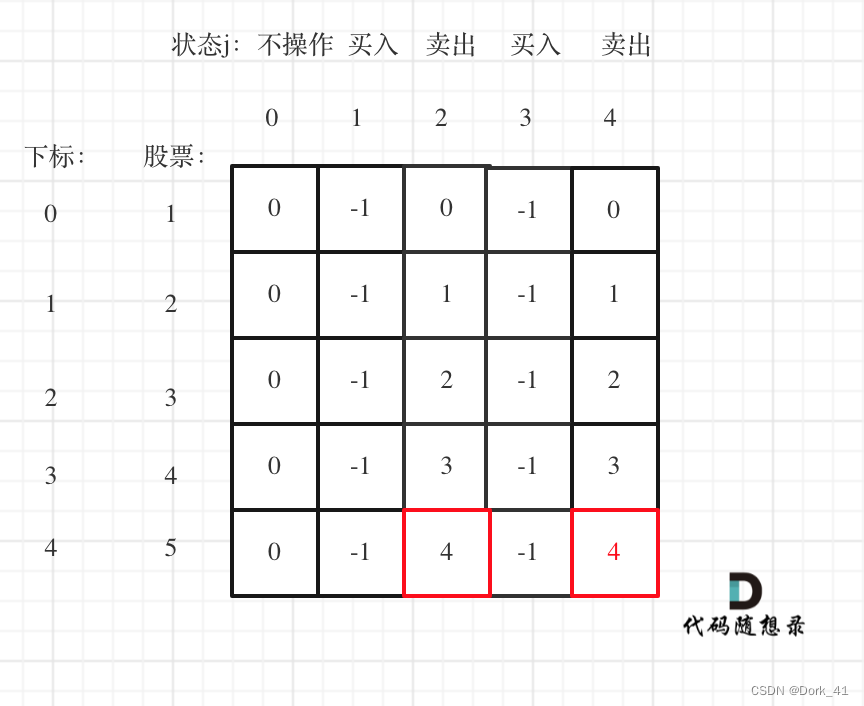
代码随想录算法训练营第四十九天| 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
文档讲解:代码随想录 视频讲解:代码随想录B站账号 状态:看了视频题解和文章解析后做出来了 123.买卖股票的最佳时机III class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices) 0:return 0dp [[0] * 5 for _ in…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
