如何学习算法
在不知其所以然的情况下,算法只是一堆离散的机械步骤,缺少背后的思想的支撑,
这些步骤之间就没有一个本质层面上的关联(先知亚里士多德早就指出:学习即联接)。
所以就跟背历史书也没多大区别。然而,知道了算法是怎样一步步被推导出来的,我们就一下拥有了大量的记忆提取线索:
对算法发现过程中的任何一个关键步骤(尤其是本质)的回忆都可能使我们能够自己动手推导出剩余的内容。
譬如你知道堆(heap)是怎样由朴素的决策树演化而来的,它又是为了解决什么问题的,你即便忘
记了具体的细节,也可以自己推导出来。
譬如你知道KMP算法的本质在于消除回溯,至于如何消除回溯却并不是那么难以推导的,所以即便
忘了也可以借助于大脑的逻辑演绎能力再现出来。
譬如你知道Tarjan算法其实只是从后序遍历经过两个优化调整而来的(其中并査集的使用其实只
是优化手段——为了能够迅速判断祖先节点是谁——而非算法本质 ——
当然,算法设计的主要任务本来就是通过问题条件中蕴含的知识来“消除冗余计算”和“避免不必要计算”,
所以你也可以说并査集的使用是关乎本质的,只不过,知道了为什么需要引入并査集,就会强烈地感觉
到一切是顺理成章的了),那这个出了名的绕人的算法也就不那么难以理解和记忆了。
譬如你知道排序的本质,就能够对什么是最优排序,为什么它是最优排序有深刻的认识。
揣摩的重要性,是怎么说都不为过的。揣摩的一些指导性的问题有:为什么要这样(为什么这是好的)?
为什么不是那样(有其它做法吗?有更好的做法吗?)?这样做是最好的吗?(为什么?能证明吗?)
这个做法跟其它的什么做法有本质联系吗?这个跟这个的区别是什么?问题的本质是什么?
这个做法的本质又是什么?到底本质上是什么东西导致了这个做法如此..?与这个问题类似的还有其它问题吗?
(同样或类似的做法也适用吗?)等等。
猜数:用二分法: 本质:为什么这种策略具有最优下界?答案也很简单,这个策略是平衡的。
这种策略的本质可以概括成“让未知世界无机可乘”。
二分搜索为什么好,就是因为它每次都将可能性排除一半并且无论如何都能排除一
半(它是最糟情况下表现最好的)。
称球:指导思想——你选择的称法必须使得当天平平衡的时候答案剩下的可能性和天平左倾(右倾)的
时候答案剩下的可能性一样多。实际上,这等同于你得选择一种称法,使得天平输出三种结果的概率
是均等的,因为天平输出某个结果的概率就等同于所有支持这个结果(左倾、右倾、平衡)的答案可
能性的和,并且答案的每个可能性都是等概率的。
排序的本质可以这样来表述:一组未排序的N个数字,它们一共有N!种重排,其中只有一种排列是满足
题意的(譬如从大到小排列)。换句话说,排序问题的可能性一共有N!种。
基排高效的本质原因:假设前i张牌都已经放到了它们对应的位置上,第i+1张牌放出去的时候,实际
上就相当于“一下子”就确立了它和前i张牌的大小关系,用O(1)的操作就将这张牌正确地插入到了
前i张牌中的正确位置上,这个效果就相当于插入排序的第i轮原本需要比较O (i)次的,现在只需要O(1)了。
当i张牌放到位之后,放置第i+1张牌的时候有多少种可能性?大约i+1种,因为前i张牌将13个位置分割成
了i+1个区间——第i+1张牌可以落在任意一个区间。所以放置第i+1张牌就好比是询问这样一个问题:
“这张牌落在哪个区间呢?”而这个问题的答案有i+1种可能性?所以它就将剩下来的可能性均分成了
i+1份(换句话说,砍掉了i/i+1的可能性!)。再看看基于比较的排序吧:由于每次比较只有两种结
果,所以最多只能将剩下的可能性砍掉一半。
只需要一种看问题的本质视角:将排序问题看成和猜数字一样,是通过问问题来缩小/排除
(narrow down)结果的可能性区间,这样一来,就会发现,“最好的问题”就是那些能够均分所有可能
性的问题,因为那样的话不管问题的答案如何,都能排除掉k- 1/k(k为问题的答案有多少种输出——猜
数字里面是2,称球里面是3)种可能性,而不均衡的问题总会有一个或一些答案分支排除掉的可能性
要小于k- 1/k。于是策略的下界就被拖累了。
思想与技术水平都是挂钩的,到了哪一层技术才能有相应的思想。
相关文章:

如何学习算法
在不知其所以然的情况下,算法只是一堆离散的机械步骤,缺少背后的思想的支撑, 这些步骤之间就没有一个本质层面上的关联(先知亚里士多德早就指出:学习即联接)。 所以就跟背历史书也没多大区别。然而…...

MFC/QT 一些快要遗忘的细节:
1:企业应用中,MFC平台除了用常见的对话框模式还有一种常用的就是单文档模式, 维护别人的代码,不容易区分,其实找与程序同名的cpp就知道了,比如项目名称为 DoCMFCDemo,那么就看BOOL CDocMFCDemoApp::InitI…...

常见的面试算法题:阶乘、回文、斐波那契数列
1.阶乘算法 Factorial 例如:给出数字5,对其以下的的每个数字相乘,结果等于120 解:递归 Recursive function factorial(n) {// 如果n为0或1,阶乘是1if (n 0 || n 1) {return 1;}// 否则,返回n乘以n-1的…...

微服务 Spring Cloud 7,Nacos配置中心的Pull原理,附源码
目录 一、本地配置二、配置中心1、以Nacos为例:2、Pull模式3、也可以通过Nacos实现注册中心 三、配置中心提供了哪些功能四、如何操作配置中心1、配置注册2、配置反注册3、配置查看4、配置变更订阅 五、主流的微服务注册中心有哪些,如何选择?…...

c#Nettonsoft.net库常用的方法json序列化反序列化
Newtonsoft.Json 是一个流行的 JSON 操作库,用于在 .NET 应用程序中序列化、反序列化和操作 JSON 数据。下面是 Newtonsoft.Json 常用的一些方法: 序列化对象为 JSON 字符串: string json JsonConvert.SerializeObject(obj);var obj new {…...

力扣刷题-二叉树-二叉树的高度与深度
二叉树最大深度 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 递归法 本题可以使用前序(中左…...

Vue3新增加的css语法糖
一、deep <template><div class""><el-input /> </div> </template> <style scoped> /* 样式穿透 */ :deep input {background: red; } </style> 二、slotted 子组件修改插槽里面的样式 <template><div clas…...
Windows安装Vmware 虚拟机
目录 一、Vmware 虚拟机介绍 二、Vmware 虚拟机的三种网络模式 2.1桥接模式 2.2仅主机模式 2.3NAT 网络地址转换模式 三、Vmware 虚拟机的安装 一、Vmware 虚拟机介绍 VMware Workstation Pro 是一款可以在个人电脑的操作系统上创建一个完全与主机操作系统隔离的 虚拟机&…...

uniapp地图手动控制地图scale
前言 首次使用uniapp开发地图过程中,发现uniapp地图居然没有提供手动控制地图scale的方法,这个也着实没有想到,查了半天资料,也终于找到一个方法能够比较好的控制scale,做个记录。 代码 要定义一个地图mapÿ…...

Kotlin学习之函数
原文链接 Understanding Kotlin Functions 函数对于编程语言来说是极其重要的一个组成部分,函数可以视为是程序的执行,是真正活的代码,为啥呢?因为运行的时候你必须要执行一个函数,一般从主函数入口,开始一…...
若依启动步骤
1.创建数据库 2.启动redis 3.改后端的数据库连接配置 4.配置redis redis的地址:cmd中ipconfig命令查看 6.启动后端:如下 7.启动前端ruoyi-ui中 先运行npm install,再npm run dev。项目就启动成功了。 用户名:admin 密码&#x…...
qt-C++笔记之两个窗口ui的交互
qt-C笔记之两个窗口ui的交互 code review! 文章目录 qt-C笔记之两个窗口ui的交互0.运行1.文件结构2.先创建widget项目,搞一个窗口ui出来3.项目添加第二个widget窗口出来4.补充代码4.1.qt_widget_interaction.pro4.2.main.cpp4.3.widget.h4.4.widget.cpp4.5.second…...
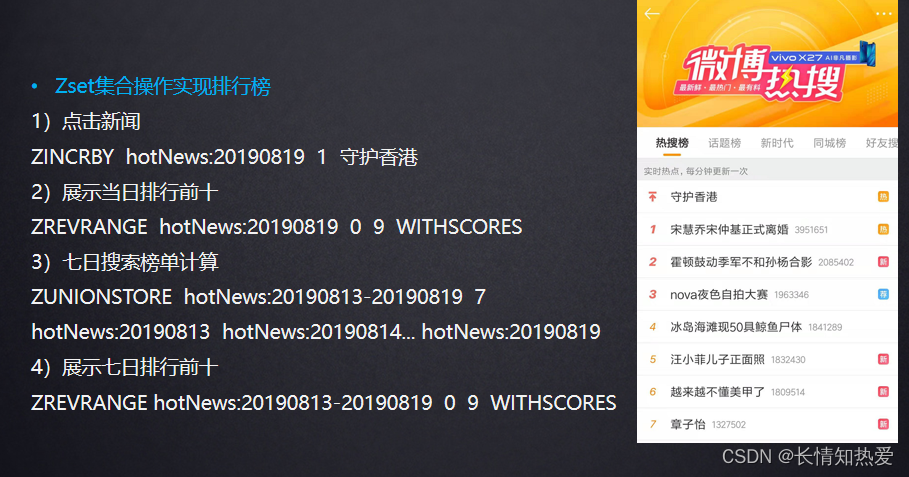
Redis-核心数据结构
五种数据结构 String结构 String结构应用场景 Hash结构 Hash结构应用场景 List结构 List结构应用场景 Set结构 Set结构应用场景 ZSet有序结构 ZSet有序结构应用场景...

设计模式—结构型模式之外观模式(门面模式)
设计模式—结构型模式之外观模式(门面模式) 外观(Facade)模式又叫作门面模式,是一种通过为多个复杂的子系统提供一个一致的接口,而使这些子系统更加容易被访问的模式。 例子 我们的电脑会有很多 组件&am…...

CentOS Stream 9-使用 systemd 管理自己程序时自定义日志路径
systemd 文件 [rootnode1 ~]# cat /etc/systemd/system/spms-wvp.service [Unit] DescriptionWVP service [Service] # 关键配置部分,注意这里的 spms-wvp ,后面需要用 SyslogIdentifierspms-wvp StandardOutputsyslog StandardErrorsyslog Typesimple Environment…...
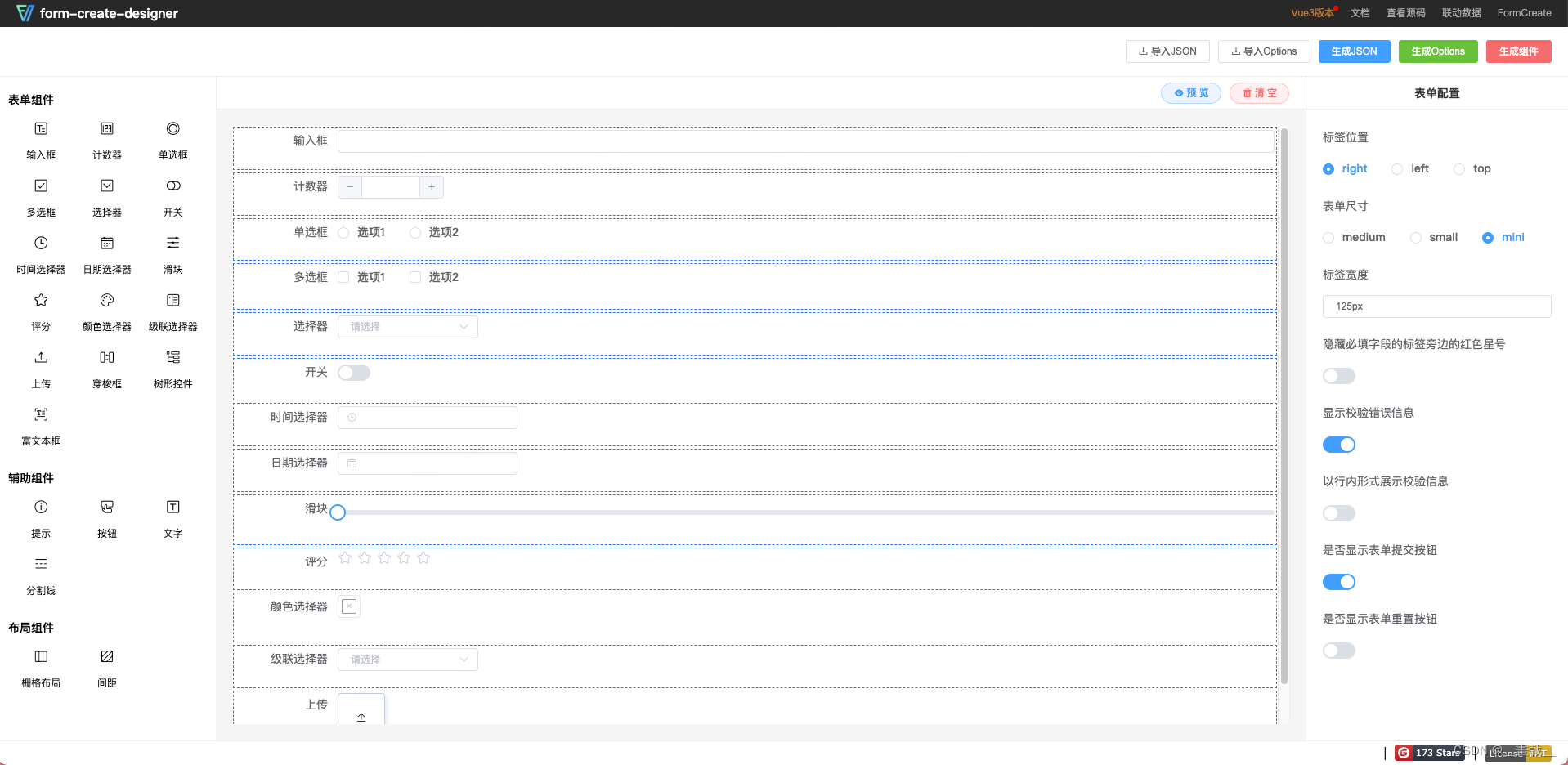
动态页面调研及设计方案
文章目录 vue2 动态表单、动态页面调研一、form-generator二、ng-form-element三、Variant Form四、form-create vue2 动态表单、动态页面调研 一、form-generator 预览:https://mrhj.gitee.io/form-generator/#/ Vue2 Element UI支持拖拽生成表单不支持其他组件…...
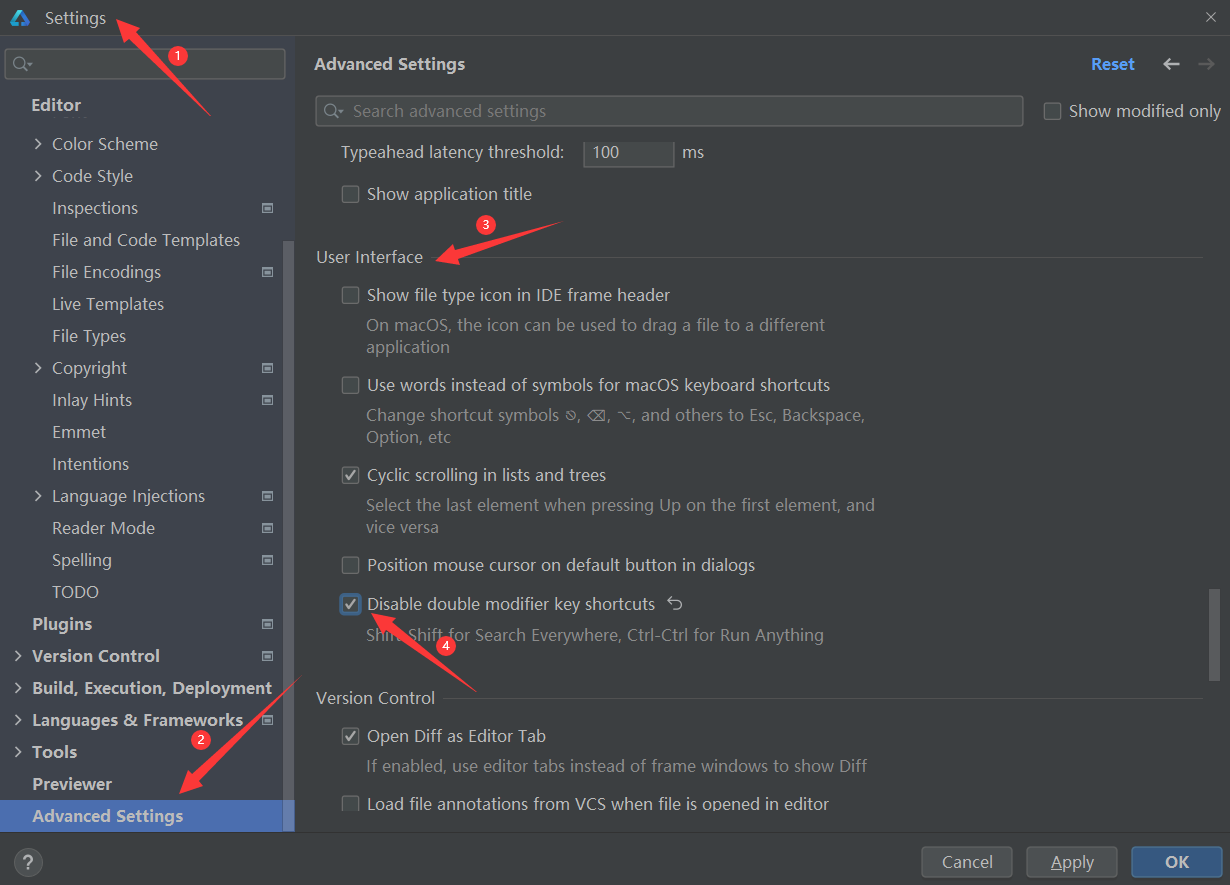
鸿蒙4.0开发笔记之DevEco Studio之配置代码片段快速生成(三)
一、作用 配置代码片段可以让我们在Deveco Studio中进行开发时快速调取常用的代码块、字符串或者某段具有特殊含义的文字。其实现方式类似于调用定义好变量,然而这个变量是存在于Deveco Studio中的,并不会占用项目的资源。 二、配置代码段的方法 1、打…...

HarmonyOS真机调试报错:INSTALL_PARSE_FAILED_USESDK_ERROR处理
文章目录 1、 新建应用时选择与自己真机匹配的sdk版本2、 根据报错提示连接打开处理方案3、查询真机版本对应的**compileSdkVersion** 和 **compatibleSdkVersion** 提示3.1版本之后和3.1版本之前的不同命令(此处为3.0版本)4、根据查询修改参数5、连接成…...

webSocket基于面向对象二次封装
今天不睡,熬夜赶了个WebSocket 二次封装,也对这几天文章摸鱼感到抱歉,所以我出了一个注释非常非常全的代码 思路如下 首先,需要通过调用connect方法来建立WebSocket连接。当连接成功时,会调用我提供的回调函数,并将连接成功的消息帧作为参数…...

【Web】PHP反序列化的一些trick
目录 ①__wakeup绕过 ②加号绕过正则匹配 ③引用绕过相等 ④16进制绕过关键词过滤 ⑤Exception绕过 ⑥字符串逃逸 要中期考试乐(悲) ①__wakeup绕过 反序列化字符串中表示属性数量的值 大于 大括号内实际属性的数量时,wakeup方法会被绕过 (php5-p…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
