时间序列与 Statsmodels:预测所需的基本概念(1)
后文:时间序列与 statsmodels:预测所需的基本概念(2)-CSDN博客
一、说明
二、时间序列介绍
时间序列通常是在固定采样间隔内随时间顺序测量的变量,从而产生时间序列形式的数据。时间序列最重要的特征之一是时间上接近的观察结果往往是相关的(序列相关)。基本上,我们基于这种序列依赖性进行所有预测,从经典的 SARIMA 模型到 LSTM 或 LGBT。时间序列中最重要的概念是趋势,季节性、周期、随机游走和白噪声。
趋势是时间序列中的系统性变化,看起来不具有周期性。相反,季节性变化是每个时期(无论采样间隔是年、月、周等)内的重复模式,并且可以在更多采样周期内重复自身。周期是一种与某些固定采样间隔不对应的模式,但它具有相同的重复模式(例如米兰科维奇周期、厄尔尼诺现象、商业周期……)。白噪声是时间序列中的纯粹随机性,当我们删除所有模式(趋势、季节性、自相关)时留下的。白噪声应该与此处定义的随机游走区分开来,并且它不是平稳过程,因为它与时间无关。
让我们看一个示例,使用非常简单且有用的包 statsmodels 来分解时间序列 - 如何提取趋势和季节性以及如何检查时间序列是否平稳。所有这些使我们能够进行预测,基本上假设现有的时间序列模式将在某个(至少)较短的未来时间继续(推断)。我们将使用可以在此处找到的著名的航空乘客数据。

航空旅客数据
三、趋势和季节性示例
现在我们将时间序列分解为趋势和季节(将采用 12 个月的输入参数)。之后我们必须检查残差的平稳性。平稳时间序列是一种其属性不依赖于观察该序列的时间的序列。因此,具有趋势或季节性的时间序列并不是静止的——趋势和季节性会影响时间序列在不同时间的值。另一方面,白噪声序列是平稳的——什么时候观察它并不重要,它在任何时间点看起来都应该大致相同。因此,我们将检查残差的平稳性,这表明我们确实做了趋势和季节性解释了时间序列的所有“模式”。
from statsmodels.tsa.seasonal import seasonal_decomposedef decomposition(timeseries, period):decomposition = seasonal_decompose(timeseries, period=period)trend = decomposition.trendseasonal = decomposition.seasonalresidual = decomposition.residplt.figure(figsize=(10, 5))plt.subplot(411)plt.plot(timeseries, label='Original')plt.legend(loc='best')plt.subplot(412)plt.plot(trend, label='Trend')plt.legend()plt.subplot(413)plt.plot(seasonal,label='Seasonality')plt.legend()plt.subplot(414)plt.plot(residual, label='Residuals')plt.legend()plt.tight_layout()plt.show(block=False)
decomposition(data, 12)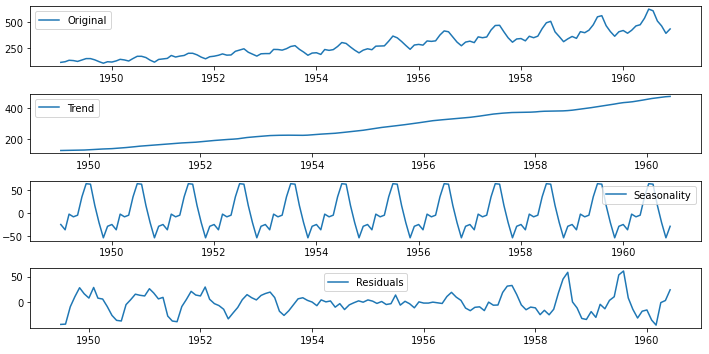
时间序列的分解
我们将使用 adfuller 检验来告诉我们零假设是否为真(时间序列不是平稳的)。
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries, rolling=12):#Determing rolling statisticsrolmean = timeseries.rolling(rolling).mean()rolstd = timeseries.rolling(rolling).std()#Plot rolling statistics:plt.figure(figsize=(10, 5))orig = plt.plot(timeseries, color='blue',label='Original')mean = plt.plot(rolmean, color='red', label='Rolling Mean')std = plt.plot(rolstd, color='black', label = 'Rolling Std')plt.title('Power consumption Old data')plt.xlabel('Time - periods(30s)')plt.ylabel('Power consumption in Watts')plt.legend(loc='best')plt.title('Rolling Mean & Standard Deviation')plt.show()#Perform Dickey-Fuller test:print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC')dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])for key,value in dftest[4].items():dfoutput['Critical Value (%s)'%key] = valueprint (dfoutput)if dfoutput['p-value'] < 0.05:print('The timeseries is stationary at 95% level of confidence')else:print('The timeseries is not stationary at 95% level of confidence')
test_stationarity(data, rolling=12)
时间序列平稳性检验结果
从结果中可以看出,残差不是平稳的,并且您可以看到标准差如何随着时间的推移而增加,这意味着时间序列中还有一些参数需要额外分析。这导致了自回归参数和移动平均线。另外,我们显然在这个时间序列中具有乘性季节性效应,这意味着季节性效应随着趋势的增加而增加(Xt = mt(趋势)* st(季节)+ zt(误差))。但是让我们注意自回归。
自回归可以很容易地理解为自相关,即时间序列与其自身在其他时间点的相关性。为此,我们使用相关图来显示不同时间点的去季节和去趋势时间序列的相关性。作为参数,我们可以输入要计算自相关的滞后数(在此数据中,我们有 144 个时间点)。
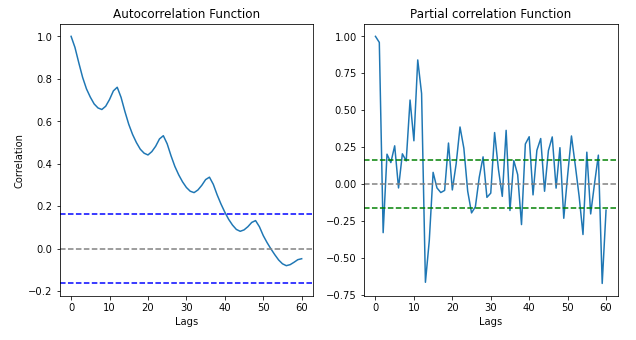
蓝色和绿色线是我们的时间序列的时间滞后的相关性和部分相关性的置信水平。
通常,如果 ACF 和 PACF 正在缓慢衰减,则意味着我们必须再做一件事,那就是求差。这应该有助于我们获得残差的平稳性,这在实践中意味着我们解释了时间序列的所有组成部分,并且我们完全“阅读”了它的模式。差分减去两个最接近的时间点。
def differencing(timeseries, second_order=False):diff = timeseries - timeseries.shift(1)diff=diff.dropna()print('Results of stationarity of the first ordered differencing')test_stationarity(diff)if second_order:diff_sec = diff - diff.shift(1)diff_sec=diff_sec.dropna()print('\n', 'Results of stationarity of the SECOND ordered differencing')test_stationarity(diff_sec)
differencing(data, False)
一阶差分并没有使时间序列平稳。
在这里我们可以看到一阶差分还没有导致平稳时间序列。我们将尝试二阶差分(已差分时间序列的差分)。
differencing(data, True)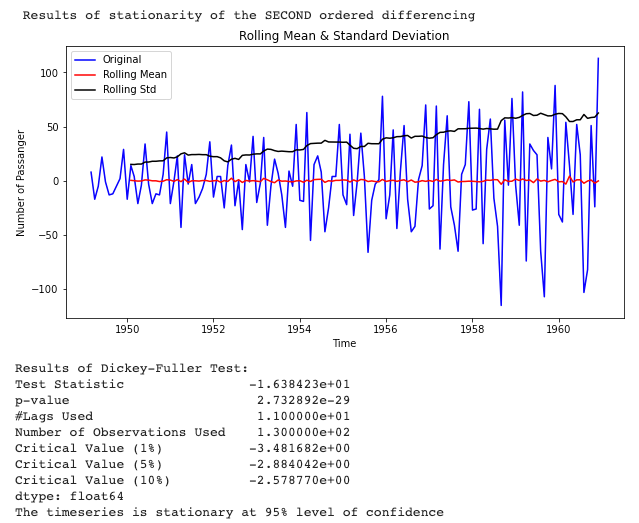
二阶差分导致时间序列的平稳性。
最后!我们得到了平稳残差。残差的平均值和标准差不随时间变化。这意味着我们在 ARIMA 中的 I 参数应该是 2。但是 AR 和 MA 呢?正如您所猜测的,AR 是自回归参数,而 MA 是移动平均线。阅读上面的相关图,我们可以得出采用哪些参数的结论。公认的规则是,我们有 ACF 的正弦模式,并且在 PACF 中跳跃,它应该是 AR = 2,这意味着我们的预测时间点将采用以下公式: Yt = b0 + b1 Yt-1 + b2 Yt-2 + wt ( wt =白噪声)。维托米尔·约万诺维奇
相关文章:

时间序列与 Statsmodels:预测所需的基本概念(1)
后文:时间序列与 statsmodels:预测所需的基本概念(2)-CSDN博客 一、说明 本博客解释了理解时间序列的基本概念:趋势、季节性、白噪声、平稳性,并使用自回归、差分和移动平均参数进行预测示例。这是理解任何…...

计算机网络(持续更新…)
文章目录 一、概述1. 计网概述⭐ 发展史⭐ 基本概念⭐ 分类⭐ 数据交换方式🥰 小练 2. 分层体系结构⭐ OSI 参考模型⭐TCP/IP 参考模型🥰 小练 二、物理层1. 物理层概述⭐ 四个特性 2. 通信基础⭐ 重点概念⭐ 极限数据传输率⭐ 信道复用技术🎉…...
BetterDisplay Pro for Mac(显示器校准软件)
BetterDisplay Pro是一款由waydabber开发的Mac平台上的显示器校准软件,可以帮助用户调整显示器的颜色和亮度,以获得更加真实、清晰和舒适的视觉体验。 以下是BetterDisplay Pro的主要特点: - 显示器校准:可以根据不同的需求和环境…...
Node.js之TCP(net)
Hi I’m Shendi Node.js之TCP(net) 最近使用Nodejs编写程序,需要用到自己编写的分布式工具,于是需要将Java版的用NodeJs重新写一遍,需要使用到TCP通信,于是在这里记录下Node.js TCP 的使用方法 依赖 需要使…...

何时使用Elasticsearch而不是MySql?
何时使用Elasticsearch而不是MySql? MySQL 和 Elasticsearch 是两种不同的数据管理系统,它们各有优劣,适用于不同的场景。本文将从以下几个方面对它们进行比较和分析: 数据模型查询语言索引和搜索分布式和高可用性能和扩展性使用…...
nodejs微信小程序 +python+PHP+图书销售管理系统的设计与实现-网上书店-图书商城-计算机毕业设计
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

云原生周刊:Istio 1.20.0 发布 | 2023.11.20
开源项目推荐 DevPod DevPod 是一款纯客户端工具,可在任何后端基于 devcontainer.json 创建可重现的开发人员环境。每个开发者环境都在一个容器中运行,并通过 devcontainer.json 进行指定。通过 DevPod 提供商,这些环境可以在任何后端创建&…...
Ajax基础(应用场景|jquery实现Ajax|注意事项)
文章目录 一、Ajax简介二、基于jquery实现Ajax三、使用Ajax注意的问题1.Ajax不要与form表单同时提交2.后端响应格式问题3、使用了Ajax作为请求后的注意事项 一、Ajax简介 AJAX(Asynchronous Javascript And XML)翻译成中文就是“异步Javascript和XML”。…...
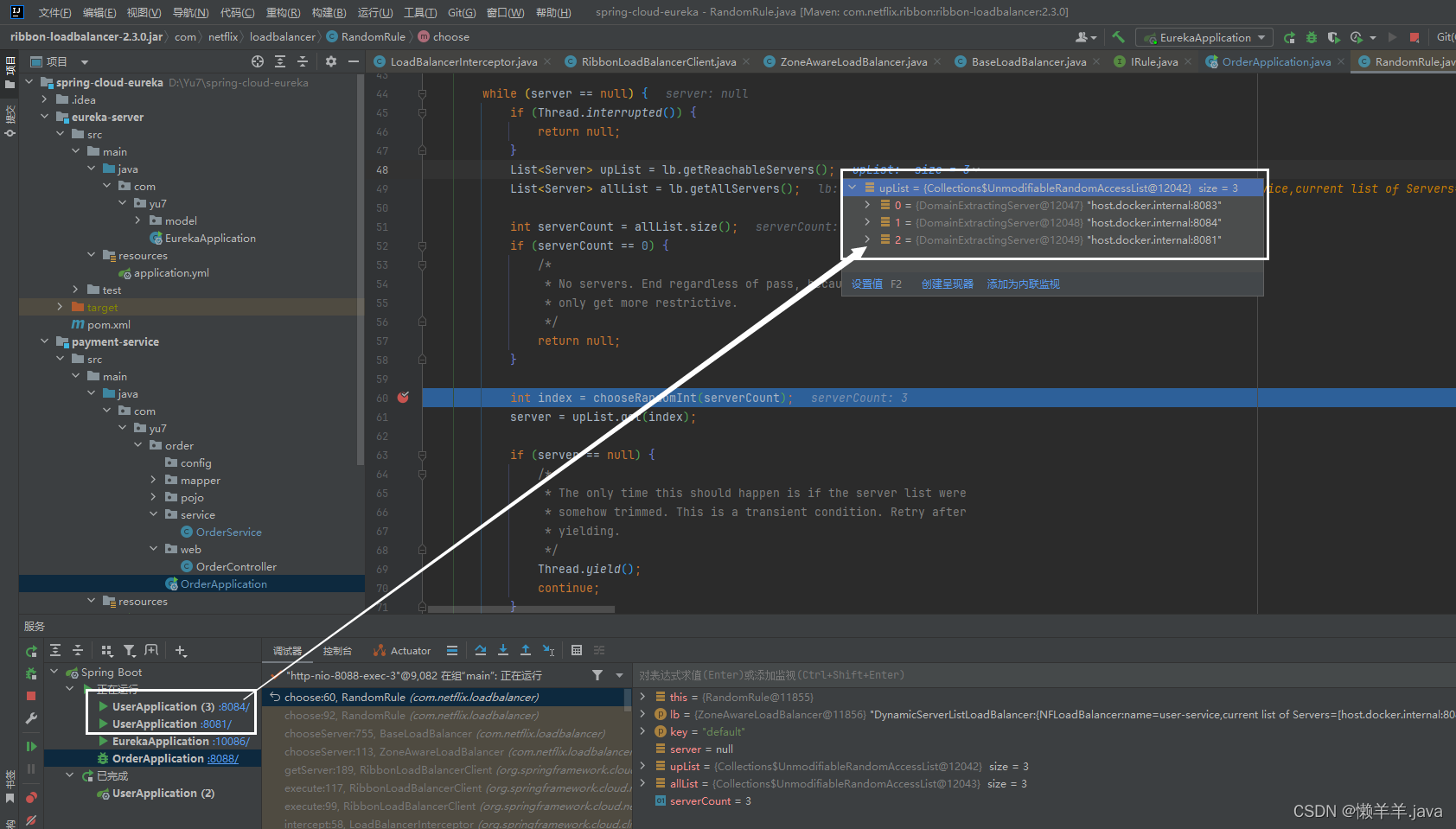
【SpringCloud】Eureka基于Ribbon负载均衡的调用链路流程分析
文章目录 前言1.调用形式2.LoadBalancerInterceptor3.负载均衡流程分析3.1 调用流程图3.2 intercept()方法3.3 execute()方法3.4 getServer()方法3.4 子类的chooseServer()方法3.5 getLoadBalancerStats().…...
+maven+mybatis)
Springboot和Vue+MYSQL项目(基本介绍+前后端结合初步项目)+maven+mybatis
一、基本知识 当我们谈论全栈开发时,通常指的是一个开发者能够处理整个应用程序的开发,包括前端(Front-End)和后端(Back-End)的所有层面。这三个基本的领域是: 前端开发(Front-End …...

基于单片机K型热电偶温度采集报警系统
**单片机设计介绍, 基于单片机K型热电偶温度采集报警系统 文章目录 一 概要简介系统特点系统组成工作原理应用领域 二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 # 基于单片机K型热电偶温度采集报警系统介绍 简介 该系统是基于单片…...

利用OpenCV做个熊猫表情包 二
之前写了一篇 利用OpenCV做个熊猫表情包吧_Leen的博客-CSDN博客 回想起来觉得有点太弱了,意犹未尽,每次使用需要自己去手动截取人脸,清除黑边什么的才能使用demo去合成表情,无奈之前由于安装的vs,opencv版本都比较低…...

华纳云服务器怎么清理cdn缓存?
清理 CDN(内容分发网络)缓存通常需要通过 CDN 提供商的管理界面或 API 进行操作。不同的 CDN 提供商可能有不同的方法和步骤,以下是一个通用的清理 CDN 缓存的一般步骤: 1. 登录到 CDN 提供商的管理界面: 打开你所使用的 CDN 提供商的网站。 …...

python functools.wraps保留被装饰函数属性
作用 普通装饰器 ,会覆盖函数名称,并且 会替换 函数 文档字符串 介绍 functools.wraps(wrapped[, assigned][, updated]) This is a convenience function for invoking partial(update_wrapper, wrappedwrapped, assignedassigned, updatedupdated) …...

【多线程 - 11、死锁】
死锁 1、介绍 在 Java 中使用多线程,就会有可能导致死锁问题。死锁会让程序一直卡住,程序不再往下执行。只能通过中止并重启的方式来让程序重新执行。要尽可能避免死锁的情况发生 2、造成死锁的原因 互斥条件: 同一资源同时只能由一个线程读…...

flask实现session开发
要在Flask应用中实现会话(session)开发,你可以使用Flask内置的session模块。以下是一个示例代码,演示在Flask应用中启用和使用会话功能: from flask import Flask, session, redirect, url_for, requestapp Flask(__…...

paddle dataset
paddle实现图像旋转 import numpy as np from PIL import Image from matplotlib import pyplot as plt from paddle.vision.transforms import functional as F import cv2imagecv2.imread(./1.jpg) imagecv2.cvtColor(image,cv2.COLOR_BGR2RGB)# 图像旋转 opencv # imgR90 …...
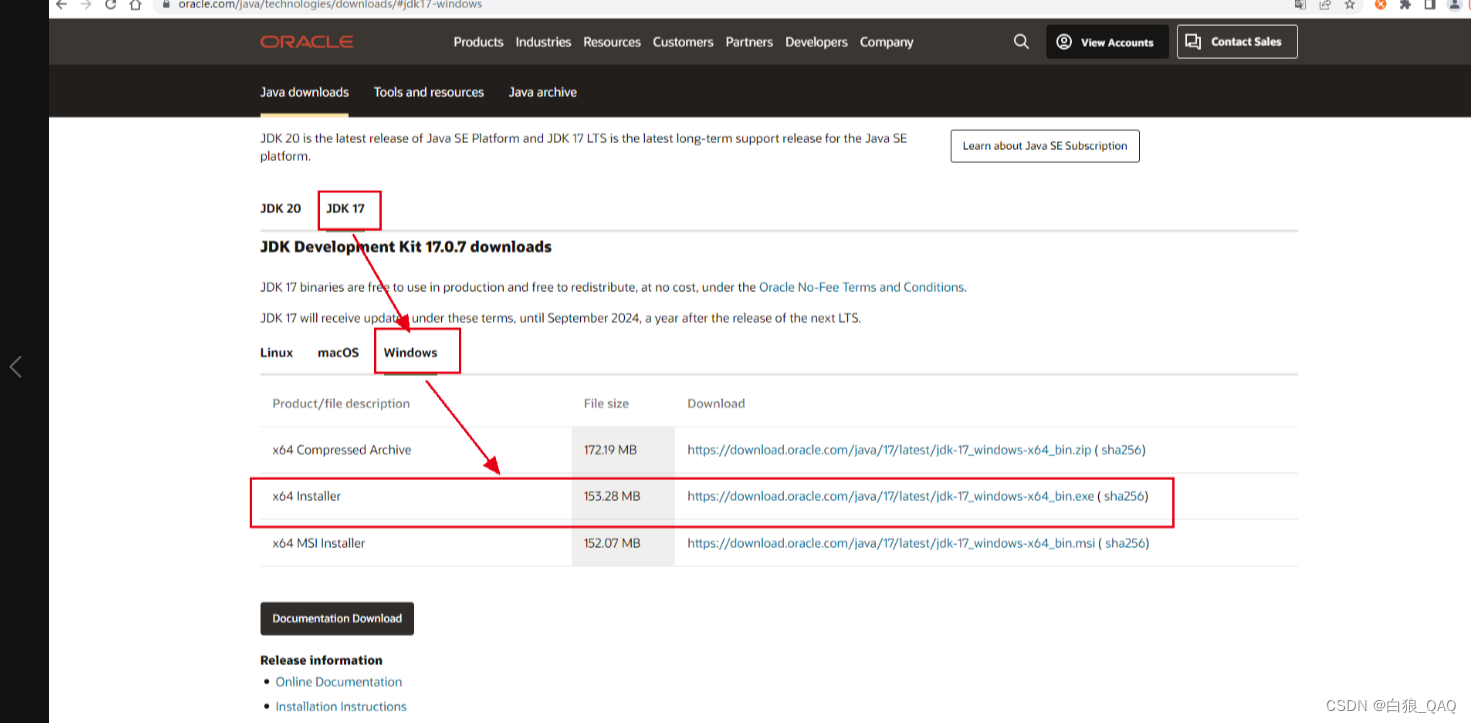
接口自动化测试实战:JMeter+Ant+Jenkins+钉钉机器人群通知完美结合
前言 一、本地JAVA环境安装配置,安装JAVA8和JAVA17 二、安装和配置Jmeter 三、安装和配置ant 四、jmeter + ant配置 五、jenkins安装和配置持续构建项目 六、jenkins配置流程 前言 搭建jmeter+ant+jenkins环境有些前提条件,那就是要先配置好java环境,本地java环境…...
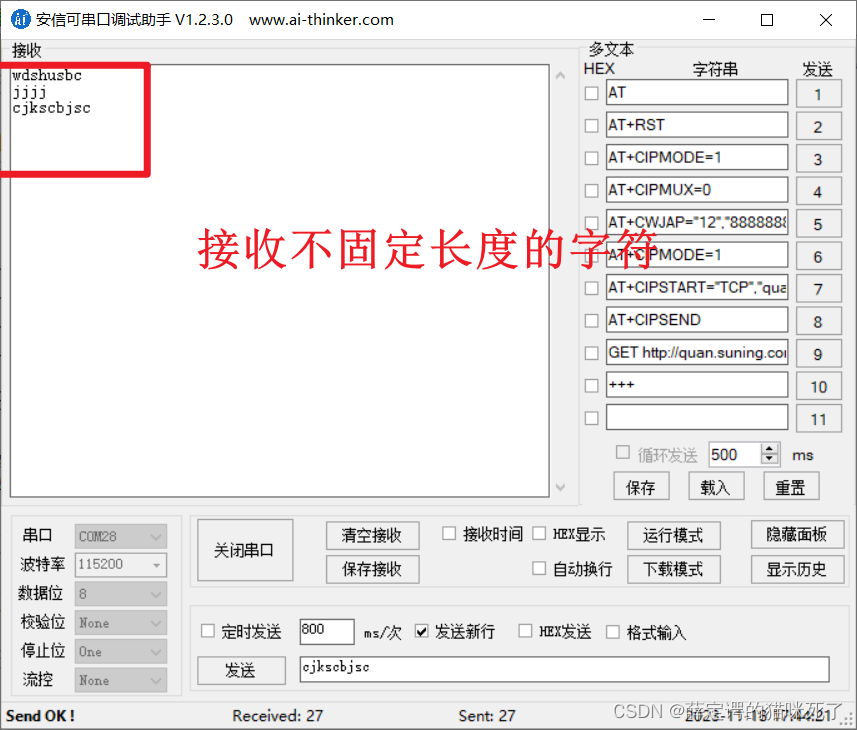
HAL库STM32串口开启DMA接收数据
STM32CubeMx的配置 此博客仅仅作为记录,这个像是有bug一样,有时候好使,有时候不好,所以趁现在好使赶紧记录一下,很多地方用到串口接收数据,DMA又是一种非常好的接收方式,可以节约CPU的时间&…...
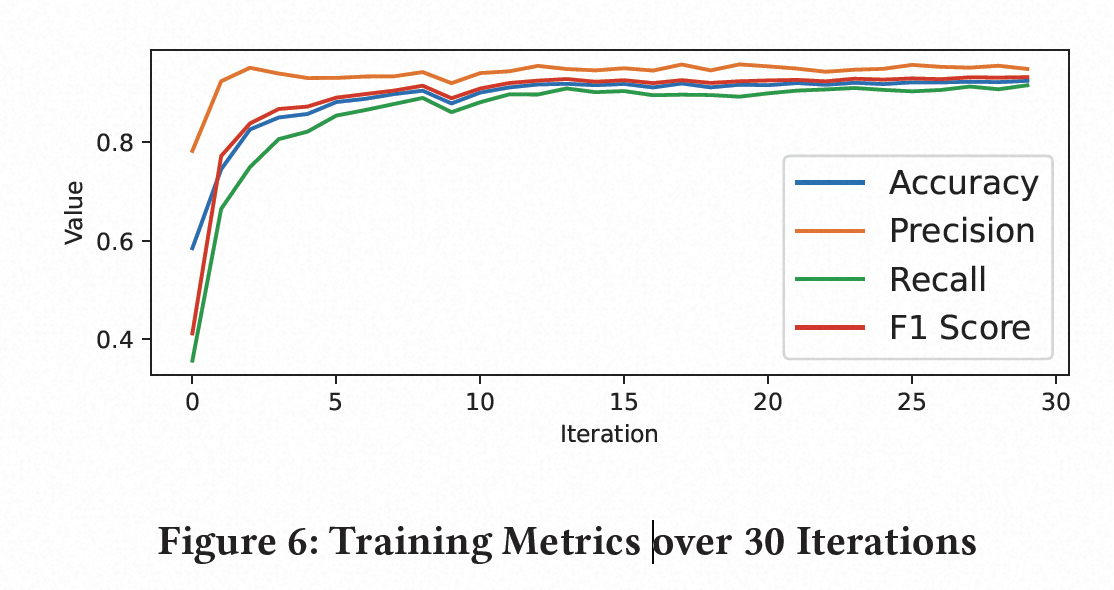
Web安全研究(五)
Automated WebAssembly Function Purpose Identification With Semantics-Aware Analysis WWW23 文章结构 introbackgroundsystem design abstraction genapplying abstractionsclassifier data collection and handling data acquisitionstatistics of collected datamodule-…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
