数理统计的基本概念(一)
文章目录
- 总体、样本与统计量
- 总体及其分布
- 样本及其分布
- 统计量
- 统计量概念
- 样本矩
- 顺序统计量及其分布
- 样本中位数与样本极差
- 经验分布函数
- 参考文献
总体、样本与统计量
总体及其分布
在数理统计中,称所研究的对象的全体为总体,总体中的元素称为个体。若总体中的个体数目为有限,则称之为有限总体;否则就称之为无限总体。
理解总体与个体:一批灯管10万支,在研究这批灯管的平均使用寿命时,该批灯管的全部使用寿命就组成一个总体,而其中每个灯管的使用寿命是个体。
数理统计所关心的并非每个个体的所有属性,而是它的某一项或若干项数量指标 X X X 和该数量指标 X X X 在总体中的分布情况。一方面,说到总体必对应某数量指标 X X X 可能取值的集合;另一方面,研究任意数量指标 X X X,其可能取值的全体即构成一个总体。因此,把二者等同起来,所谓总体的分布就是指数量指标 X X X 的分布。
数量指标 X X X 是一个随机变量,于是总体的分布也就是随机变量 X X X 的概率分布。
样本及其分布
从总体中取得一部分个体,这一部分个体称为样本。样本中的每个个体称为样品。样品中的个体数目称为样本容量。
取得样本的过程称为抽样,抽样中采用的方法称为抽样法。在数理统计中,一般采用随机抽样法,即从总体中随意地抽取若干个个体。
设由样本 X 1 , . . . , X n X_1,...,X_n X1,...,Xn,若 X 1 , . . . , X n X_1,...,X_n X1,...,Xn 是独立同分布的且 X 1 X_1 X1 的分布与总体 X X X 的分布相同,则称它为简单随机样本。
说样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 是 n n n 维随机向量,这是针对进行一次抽样前而言,实施了一次抽样后,得到的是一个实向量 ( x 1 , . . . x n ) T (x_1,...x_n)^T (x1,...xn)T,它是样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 的一个观察值,称为样本值。
统计量
统计量概念
样本是推断总体特性的依据,但在获得样本之后,并不能由样本直接进行统计推断,需要先对样本进行加工和提炼,把样本中所含的总体的相关信息集中起来,即,针对不同的问题构造出样本的适当函数。这种样本的函数就称为统计量。
设 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 为总体 X X X 的一个样本,若 g ( x 1 , . . . , x n ) g(x_1,...,x_n) g(x1,...,xn) 为样本空间 X \mathcal{X} X 到 R k \mathbf{R}^k Rk 的可测映射,且 g g g 中不含任何未知参数,则称 t = g ( X 1 , . . . , X n ) t=g(X_1,...,X_n) t=g(X1,...,Xn) 为统计量。
粗略来说,统计量就是用作统计的量,因而它不能含未知参数。
样本矩
设 ( X 1 , . . . , X n ) (X_1,...,X_n) (X1,...,Xn) 为总体 X X X 的一个样本,称统计量 X ˉ = 1 n ∑ i = 1 n X i \bar{X}=\frac{1}{n}\sum_{i=1}^n X_i Xˉ=n1i=1∑nXi 为样本均值;称统计量 S 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = 1 n ∑ i = 1 n X i 2 − X ˉ 2 S^2=\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2=\frac{1}{n}\sum_{i=1}^n X_i^2 - \bar{X}^2 S2=n1i=1∑n(Xi−Xˉ)2=n1i=1∑nXi2−Xˉ2 及 S ∗ 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^{*2}=\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2 S∗2=n−11i=1∑n(Xi−Xˉ)2 分别为样本方差及修正样本方差,称样本方差的算数根 S = S 2 S=\sqrt{S^2} S=S2 为样本标准差;称统计量 A k = 1 n ∑ i = 1 n X i k A_k=\frac{1}{n}\sum_{i=1}^n X_i^k Ak=n1i=1∑nXik 及 B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k B_k=\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^k Bk=n1i=1∑n(Xi−Xˉ)k 分别为样本 k k k 阶原点矩及样本 k k k 阶中心矩。
由大数定律可以证明,当 n n n 很大时,可用一次抽样后所得的样本均值 x ˉ \bar{x} xˉ 和样本方差 s 2 s^2 s2 分别作为总体 X X X 的均值 μ \mu μ 和方差 σ 2 \sigma^2 σ2 的近似值。
顺序统计量及其分布
设 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 为总体 X X X 的一个样本,其观察值为 ( x 1 , . . . , x n ) T (x_1,...,x_n)^T (x1,...,xn)T,将 x 1 , . . . , x n x_1,...,x_n x1,...,xn 由小到大进行排列,依次记为 x ( 1 ) , . . . , x ( n ) x_{(1)},...,x_{(n)} x(1),...,x(n),即 x ( 1 ) ≤ . . . ≤ x ( n ) x_{(1)}\le...\le x_{(n)} x(1)≤...≤x(n)。按下述方法定义统计量 X ( k ) X_{(k)} X(k):当样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 取值为 ( x 1 , . . . , x n ) T (x_1,...,x_n)^T (x1,...,xn)T 时,规定 X ( k ) X_{(k)} X(k) 取值为 x ( k ) x_{(k)} x(k),由此得到的 ( X ( 1 ) , . . . , X ( n ) ) T (X_{(1)},...,X_{(n)})^T (X(1),...,X(n))T 称为样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 的顺序统计量或次序统计量, X ( k ) X_{(k)} X(k) 称为样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 的第 k k k 个顺序统计量, X ( 1 ) X_{(1)} X(1) 称为样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 的最小顺序统计量, X ( n ) X_{(n)} X(n) 称为样本 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 的最大顺序统计量。
样本中位数与样本极差
设 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 为总体 X X X 的一个样本,其顺序统计量为 ( X ( 1 ) , . . . , X ( n ) ) T (X_{(1)},...,X_{(n)})^T (X(1),...,X(n))T,由 ( X ( 1 ) , . . . , X ( n ) ) T (X_{(1)},...,X_{(n)})^T (X(1),...,X(n))T 可定义在应用上有重要意义的样本中位数与样本极差。
称统计量
M e = { X ( ( n + 1 ) / 2 ) , n 为奇数 1 2 ( X ( n / 2 ) + X ( ( n + 1 ) / 2 ) ) , n 为偶数 Me=\begin{cases} X_{((n+1)/2)}, &n 为奇数 \\ \frac{1}{2}(X_{(n/2)}+X_{((n+1)/2)}), &n 为偶数 \end{cases} Me={X((n+1)/2),21(X(n/2)+X((n+1)/2)),n为奇数n为偶数
为样本中位数。样本中位数具有计算方便且不受样本值中的异常值 (outlier) 影响的特点,因而有时比样本均值更具有代表性。
称统计量
R = X ( n ) − X ( 1 ) R=X_{(n)}-X_{(1)} R=X(n)−X(1)
为样本极差。样本极差是反映样本值分散程度的量。
经验分布函数
设 ( X 1 , . . . , X n ) T (X_1,...,X_n)^T (X1,...,Xn)T 为总体 X X X 的一个样本,其顺序统计量为 ( X ( 1 ) , . . . , X ( n ) ) T (X_{(1)},...,X_{(n)})^T (X(1),...,X(n))T。当样本的观察值为 ( x 1 , . . . , x n ) T (x_1,...,x_n)^T (x1,...,xn)T 时,顺序统计量的观察值为 ( x ( 1 ) , . . . , x ( n ) ) T (x_{(1)},...,x_{(n)})^T (x(1),...,x(n))T,对任意实数 x x x,记 F n ( x ) = { 0 , x < x ( 1 ) k n , x ( k ) ≤ x < x ( k + 1 ) , k = 1 , 2 , . . . , n − 1 1 , x ( n ) ≤ x F_n(x)=\begin{cases}0, &x<x_{(1)}\\ \frac{k}{n}, &x_{(k)}\le x <x_{(k+1)},k=1,2,...,n-1\\ 1, &x_{(n)}\le x \end{cases} Fn(x)=⎩ ⎨ ⎧0,nk,1,x<x(1)x(k)≤x<x(k+1),k=1,2,...,n−1x(n)≤x 则称 F n ( x ) F_n(x) Fn(x) 是经验分布函数。
经验分布函数的性质:
- F n ( x ) F_n(x) Fn(x) 是 x x x 的单调非降函数;
- F n ( x ) F_n(x) Fn(x) 是 x x x 的右连续函数;
- F n ( − ∞ ) = 0 , F n ( + ∞ ) = 1 F_n(-\infty)=0,F_n(+\infty)=1 Fn(−∞)=0,Fn(+∞)=1
参考文献
[1] 《应用数理统计》,施雨,西安交通大学出版社。
相关文章:
)
数理统计的基本概念(一)
文章目录 总体、样本与统计量总体及其分布样本及其分布统计量统计量概念样本矩顺序统计量及其分布样本中位数与样本极差经验分布函数 参考文献 总体、样本与统计量 总体及其分布 在数理统计中,称所研究的对象的全体为总体,总体中的元素称为个体。若总体…...
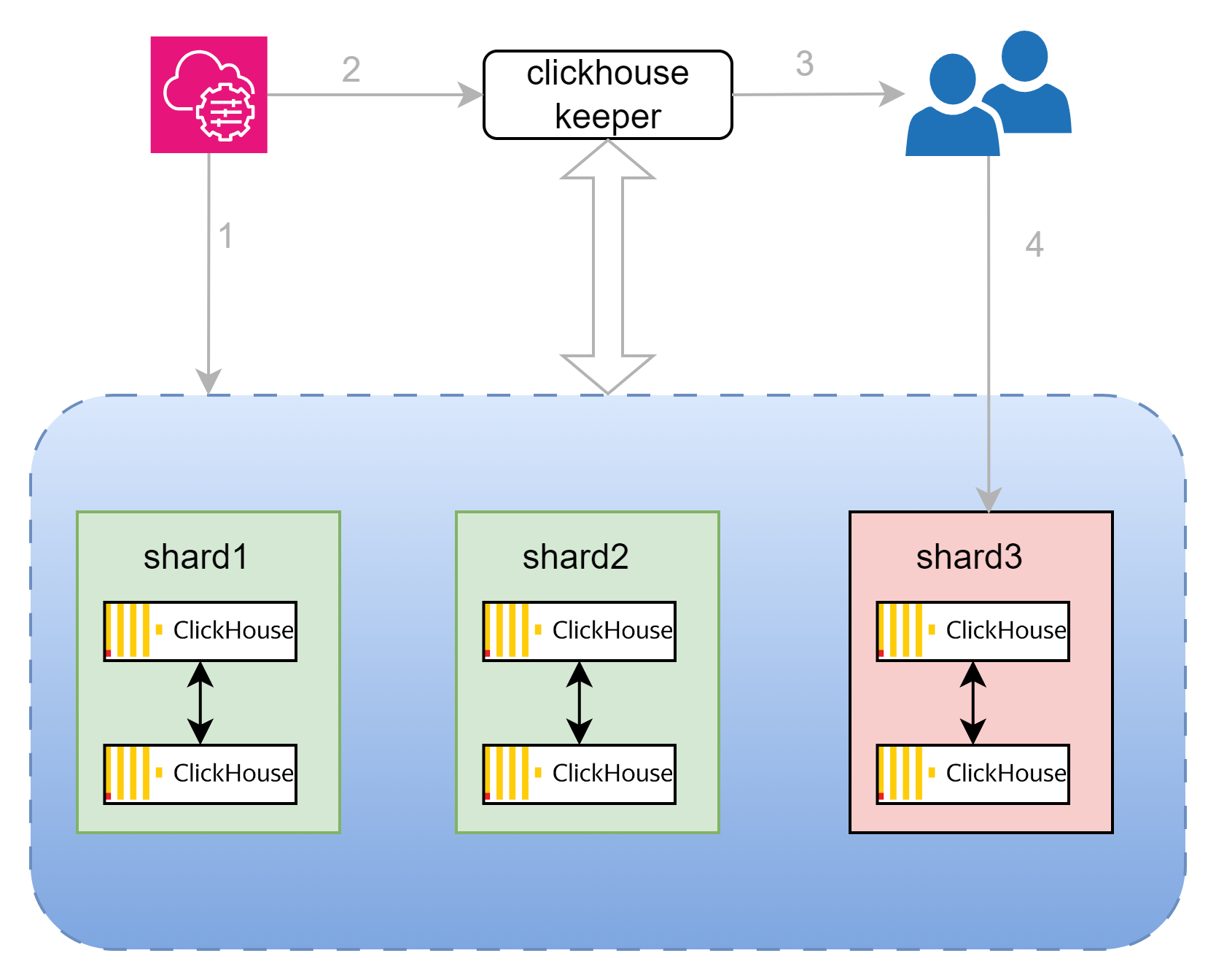
clickhouse分布式之弹性扩缩容的故事
现状 社区不支持喔,以后也不会有了。曾经尝试过,难道是是太难了,无法实现吗?因为他们企业版支持了,可能是利益相关吧,谁知道呢,毕竟开源也要赚钱,谁乐意一直付出没有回报呢。 社区…...
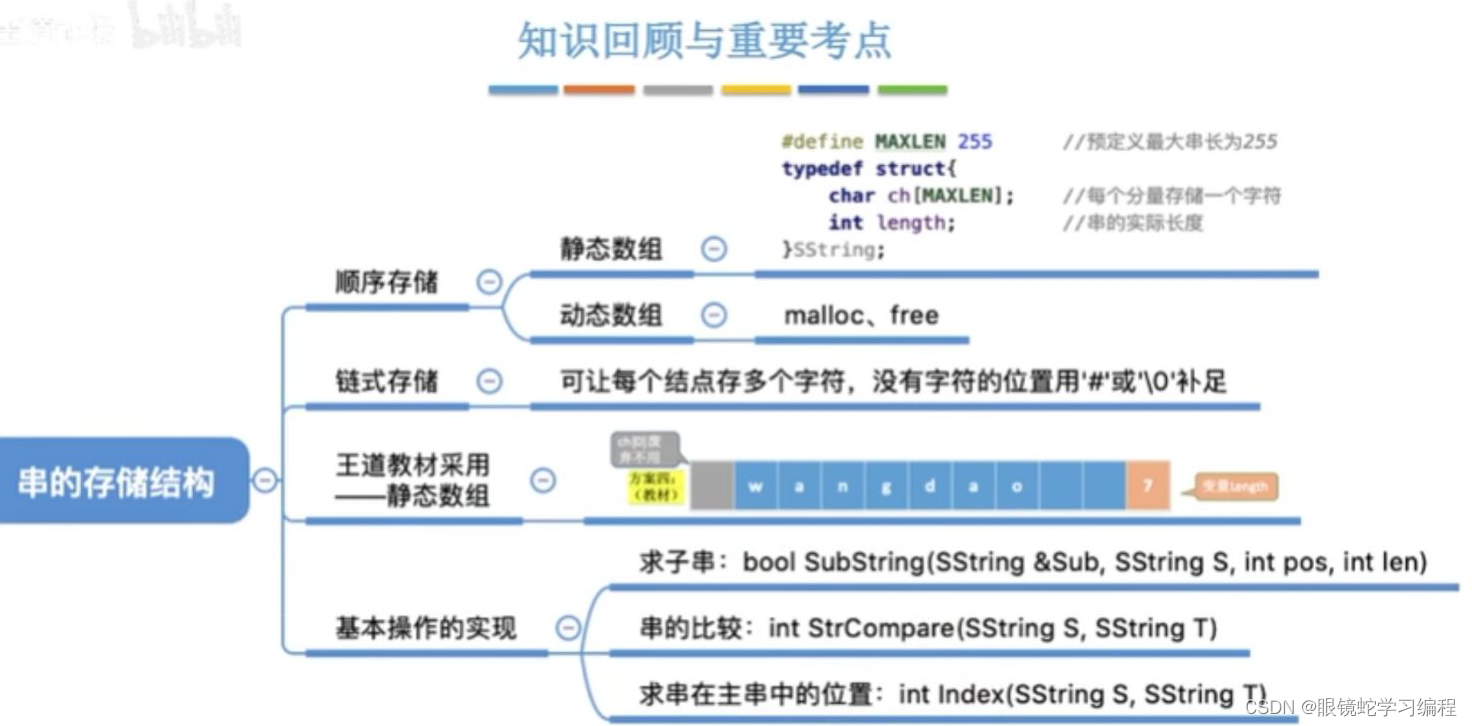
数据结构--串的基本概念
目录 串的基本概念 串的定义 串与线性表对比 串的基本操作 串的比较 字符集编码 乱码问题编辑 总结 串的存储结构 串的顺序存储编辑 串的链式存储 串的基本操作 1、求字串 2、比较 3、定位操作 总结 串的基本概念 串的定义 串与线性表对比 串的…...

音视频流媒体之 IJKPlayer FFmpeg Android 编译
FIJK dockerfile 编译环境 FROM --platformlinux/amd64 ubuntu:18.04RUN apt-get update && apt-get install -y \wget \unzip \git \gcc \g \make \python \yasm \pkg-config \protobuf-compiler \sudoRUN apt-get install -y openjdk-8-jdkENV ANDROID_HOME…...
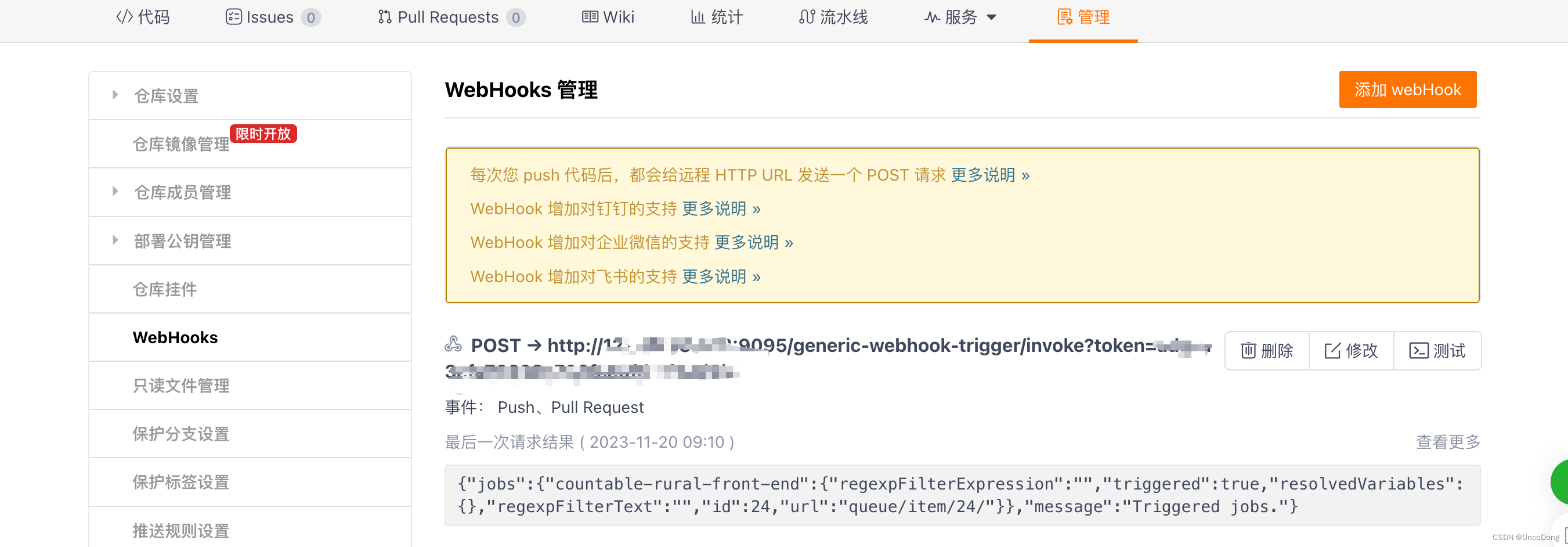
记录一次较为完整的Jenkins发布流程
文章目录 1. Jenkins安装1.1 Jenkins Docker安装1.2 Jenkins apt-get install安装 2. 关联github/gitee服务与webhook2.1 配置ssh2.2 Jenkins关联2.3 WebHook 3. 前后端关联发布 1. Jenkins安装 1.1 Jenkins Docker安装 Docker很好,但是我没有玩明白如何使用Docke…...
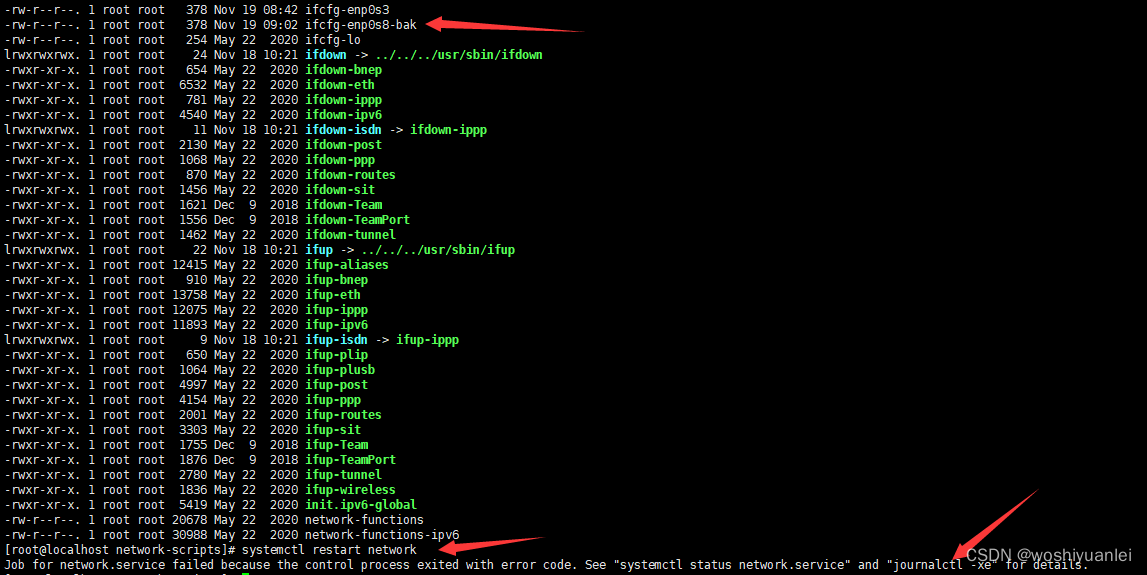
Virtual安装centos后,xshell连接centos 测试及遇到的坑
首先来一张官方的图--各种网络模式对应的连接状况: 1. 网络使用Host-Only模式动态分配IP,点确定后,centos 上运行 system restart network ,使用ifconfig查看新的ip,XShell可以直接连上centos, 但是由于使用…...
)
【算法】最优乘车——bfs(stringsteam的实际应用,getline实际应用)
题目 H 城是一个旅游胜地,每年都有成千上万的人前来观光。 为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路。 每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,…...
『亚马逊云科技产品测评』活动征文|通过lightsail一键搭建Drupal VS 手动部署
『亚马逊云科技产品测评』活动征文|通过lightsail一键搭建Drupal 提示:授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚…...

使用 VuePress 和 Vercel 打造个人技术博客:实现自动化部署
什么是VuePress? 以下是VuePress官方文档的介绍:VuePress 是一个以 Markdown 为中心的静态网站生成器。你可以使用 Markdown 来书写内容(如文档、博客等),然后 VuePress 会帮助你生成一个静态网站来展示它们。VuePress 诞生的初…...
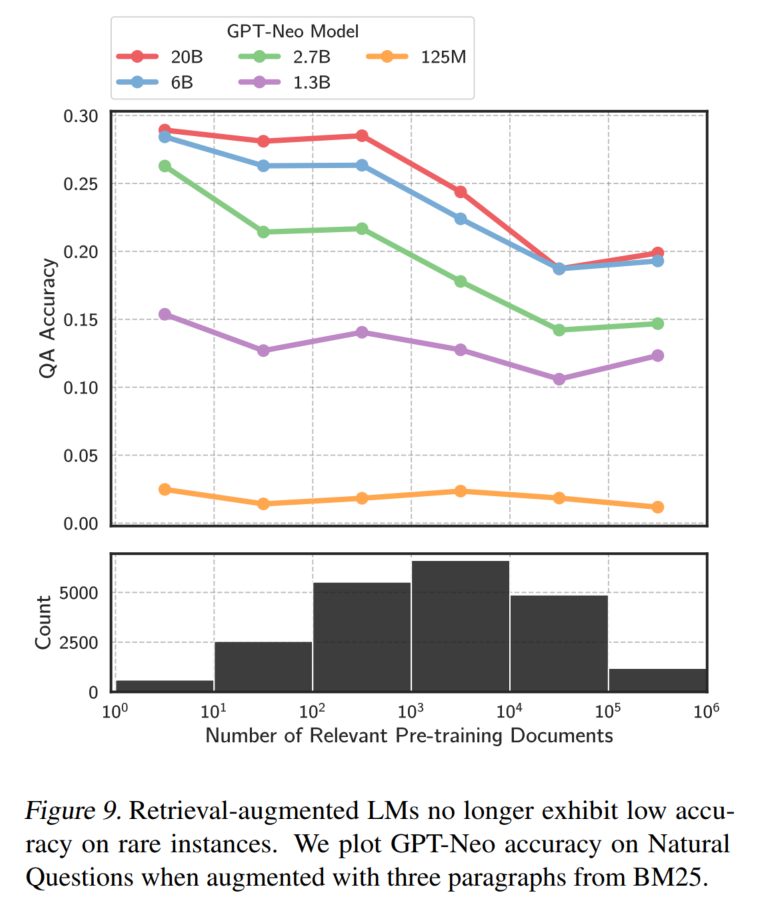
Re50:读论文 Large Language Models Struggle to Learn Long-Tail Knowledge
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文名称:Large Language Models Struggle to Learn Long-Tail Knowledge ArXiv网址:https://arxiv.org/abs/2211.08411 官方GitHub项目(代码和实体)…...
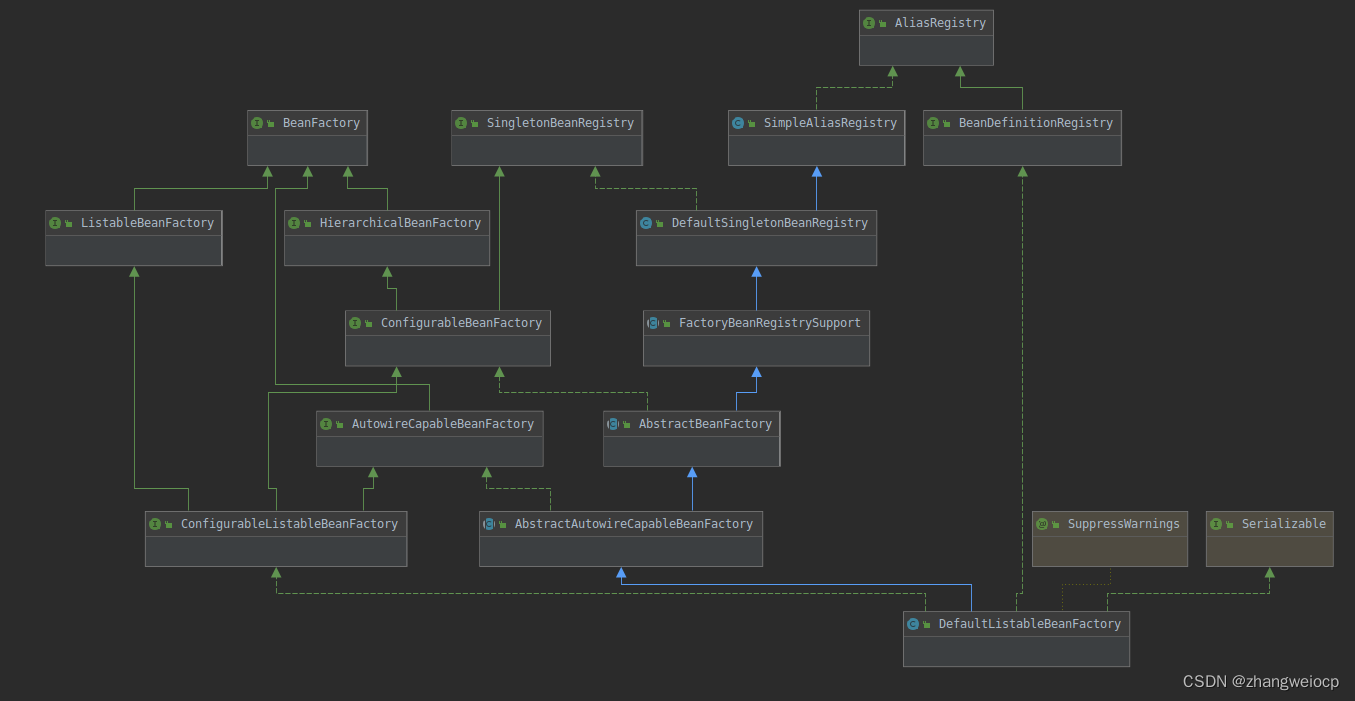
Spring IOC - Bean的生命周期之依赖注入
在Spring启动流程中,创建的factoryBean是DefaultListableBeanFactory,其类图如下所示: 可以看到其直接父类是AbstractAutoireCapableBeanFactory,他主要负责完成Bean的自动装配和创建工作。 具体来说,AbstractAutowire…...
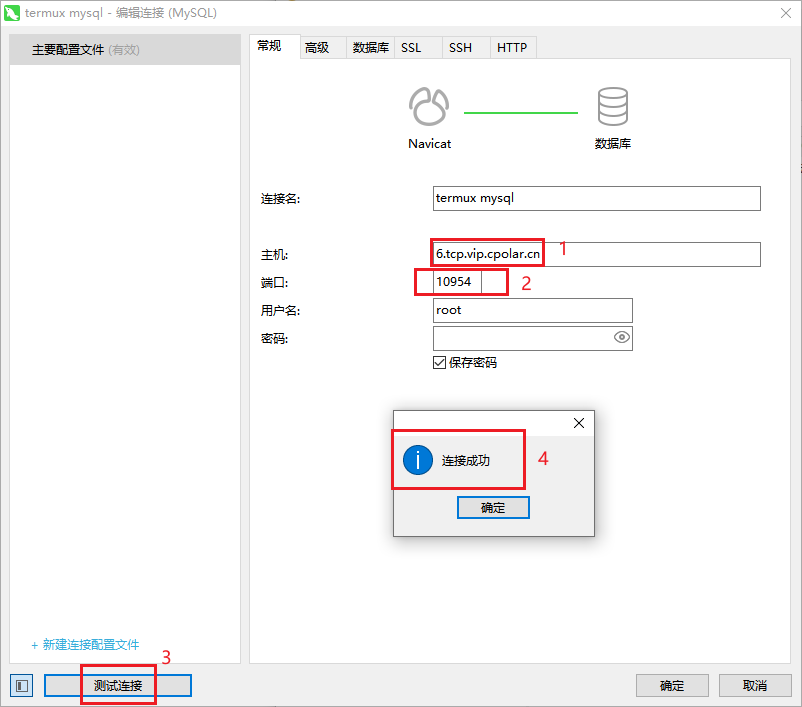
Android Termux安装MySQL,内网穿透实现公网远程访问
文章目录 前言1.安装MariaDB2.安装cpolar内网穿透工具3. 创建安全隧道映射mysql4. 公网远程连接5. 固定远程连接地址 前言 Android作为移动设备,尽管最初并非设计为服务器,但是随着技术的进步我们可以将Android配置为生产力工具,变成一个随身…...
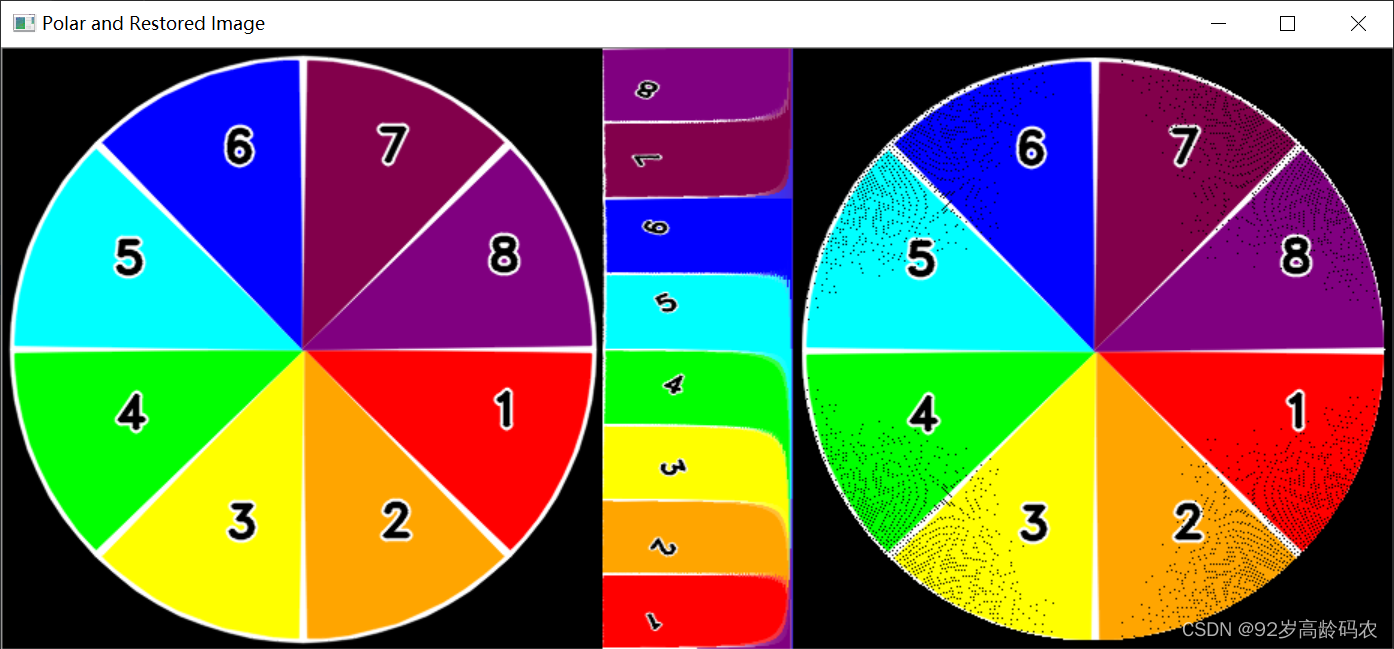
OpenCV快速入门:像素操作和图像变换
文章目录 前言1. 像素操作1.1 像素统计1.2 两个图像之间的操作1.2.1 图像加法操作1.2.3 图像加权混合 1.3 二值化1.4 LUT(查找表)1.4.1 查找表原理1.4.2 代码演示 2 图像变换2.1 旋转操作2.1.1 旋转的基本原理2.1.2 代码实现 2.2 缩放操作2.3 平移操作2.…...
Django 路由配置(二)
一、路由 就是根据用户请求的URL链接来判断对应的出来程序,并返回处理结果,也是就是URL和django的视图建立映射关系. 二、Django请求页面的步骤 1、首先Django确定要使用的根URLconf模块,通过ROOT_URLCONF来设置,在settings.py配置…...

电子学会C/C++编程等级考试2022年06月(一级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:倒序输出 依次输入4个整数a、b、c、d,将他们倒序输出,即依次输出d、c、b、a这4个数。 时间限制:1000 内存限制:65536输入 一行4个整数a、b、c、d,以空格分隔。 0 < a,b,c,d < 108输出 一行4个整数d、c、b、a,整数之…...
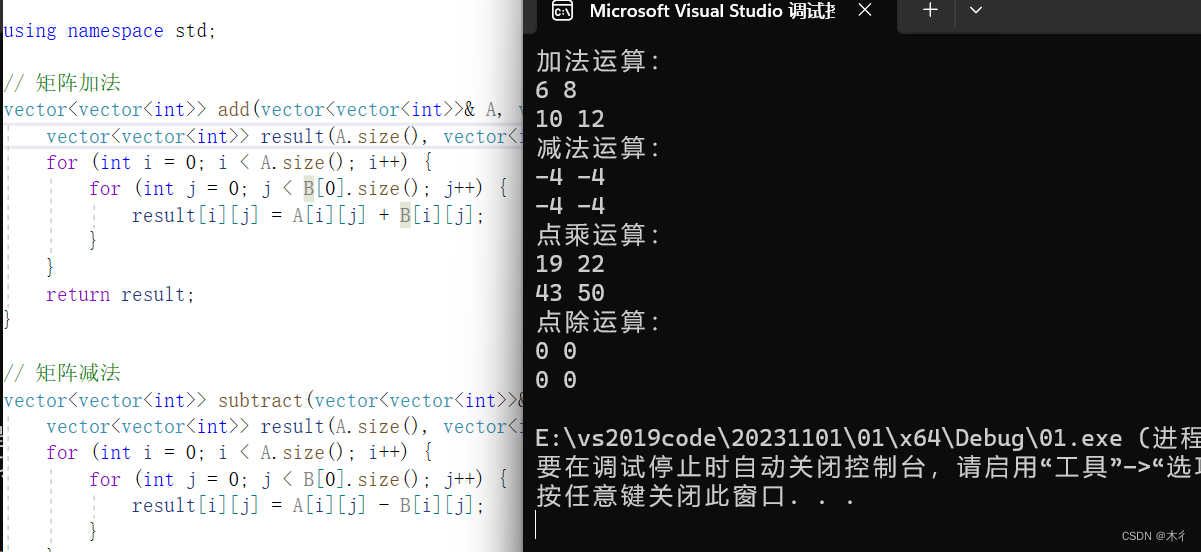
【C++】使用std::vector()函数实现矩阵的加、减、点乘、点除等运算
本文通过vector()函数表示矩阵的形式,对 加、减、点乘、点除等运算进行编码和运行,相应结果如下文所述。 #include <iostream> #include <vector>using namespace std;// 矩阵加法 vector<vector<int>> …...
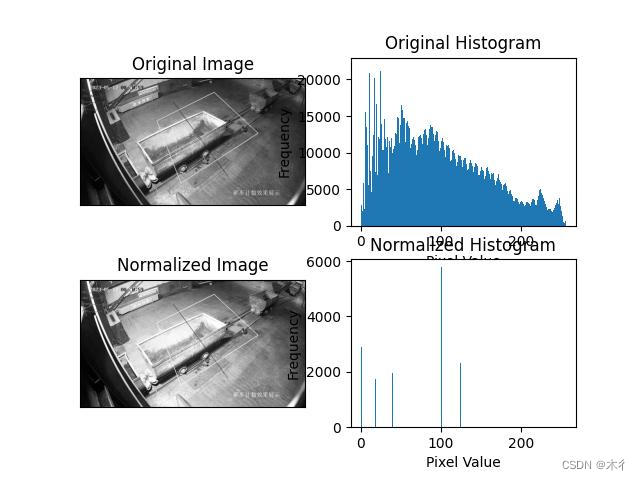
【python】直方图正则化详解和示例
直方图正则化(Histogram Normalization)是一种图像增强技术,目的是改变图像的直方图以改善图像的质量。具体来说,它通过将图像的直方图调整为指定的形状,以增强图像的对比度和亮度。 直方图正则化的基本步骤如下&…...

c语言:矩阵交换
题目: 代码和思路: #define _CRT_SECURE_NO_WARNINGS #include<stdio.h>int main() {int n 0;int m 0;int arr[10][10] { 0 }; // 输入行和列scanf("%d%d", &n, &m);int i 0;int j 0;//读取数组for (i 0; i < n; i)…...
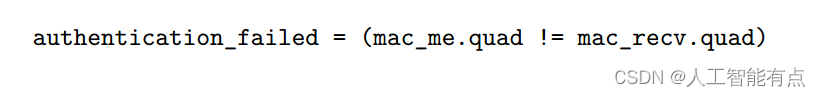
【论文阅读】基于隐蔽带宽的汽车控制网络鲁棒认证(一)
文章目录 Abstract第一章 引言1.1 问题陈述1.2 研究假设1.3 贡献1.4 大纲 第二章 背景和相关工作2.1 CAN安全威胁2.1.1 CAN协议设计2.1.2 CAN网络攻击2.1.3 CAN应用攻击 2.2 可信执行2.2.1 软件认证2.2.2 消息身份认证2.2.3 可信执行环境2.2.4 Sancus2.2.5 VulCAN 2.3 侧信道攻…...

暖阳脚本_ 将Agent技术的灵活性引入RPA,清华等发布自动化智能体ProAgent
RPA暖阳脚本 近日,来自清华大学的研究人员联合面壁智能、中国人民大学、MIT、CMU 等机构共同发布了新一代流程自动化范式 “智能体流程自动化” Agentic Process Automation(APA),结合大模型智能体帮助人类进行工作流构建&#x…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
