算法通关村第十六关黄金挑战——求滑动窗口中的最大值(滑动窗口与堆方法、双端队列法和直接比较法)
大家好,我是怒码少年小码。
今天这篇就讲一道题目,不难😎,但是一定要学会自己思考。
滑动窗口最大值
LeetCode 239:给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
示例 1:
- 输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
- 输出:[3,3,5,5,6,7]
解释:滑动窗口的位置 __ 窗口内的最大值
- [1 3 -1] -3 5 3 6 7 _______
3 - 1 [3 -1 -3] 5 3 6 7 _______
3 - 1 3 [-1 -3 5] 3 6 7 _______
5 - 1 3 -1 [-3 5 3] 6 7 _______
5 - 1 3 -1 -3 [5 3 6] 7 _______
6 - 1 3 -1 -3 5 [3 6 7] _______
7
直接比较法
首先,我第一个想到的是滑动窗口+直接比较的方法,既然是求每次滑动窗口的最大值,那就维护两个指针,当两个指针每次移动的时候都求一下当前窗口内的最大值,求出后放到存放最大值的数组中。这样一直到右指针到达数组的末尾。
public int[] maxSlidingWindow(int[] nums, int k) {int left = 0;int right = k - 1;int len = nums.length- k + 1 ;int[] maxList = new int[len];while(right < nums.length){int max = nums[left];for(int i = left ; i <= right ; i++ ){if(nums[i] > max){max = nums[i];}}maxList[left] = max;left++;right++;}return maxList;
}
当然,很不幸,这种方法超出了时间限制😎🤏🕶 -> 😭。接下来讲的方法才是本篇的重点。
滑动窗口与堆
本题初始时,我们将数组 nums 的前 k个元素放入优先队列中。每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除。
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 (num,index),表示元素num 在数组中的下标为index。
public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;//定义优先级队列,自定义排序器,首先按照nums元素值进行降序排序,如果元素值相等,则按照数组下标值进行降序排序PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>(){public int compare(int[] pair1 , int[] pair2){return pair1[0] != pair2[0] ? pair2[0]-pair1[0]:pair2[1]-pair1[1];}});// 前k个元素入队for(int i =0;i < k ; i++){pq.offer(new int[]{nums[i],i});}// 初始化结果数组int[] ans = new int[n - k + 1];ans[0] = pq.peek()[0];// 开始滑动窗口for(int i = k ; i < n ; i++){// 新的元素入队pq.offer(new int[]{nums[i],i});// 因为已经排好序,因此可以通过peek剔除掉当前队列中为最大值但非窗口中的的元素,循环结束后则队首元素为当前队列中为最大值且是窗口中的元素while(pq.peek()[1] <= i - k){pq.poll();}ans[i - k + 1] = pq.peek()[0];}return ans;
}
首先,我们有一个整数数组 nums 和一个窗口大小 k。我们需要找到每个窗口中的最大值,并将这些最大值存储在一个新的数组 ans 中。
代码的核心是使用优先队列(PriorityQueue)来维护窗口中的元素,并根据它们的值和索引进行比较。
首先,我们创建一个优先队列 pq,并通过传入一个自定义的比较器来定义元素的比较规则。比较器中的比较规则是根据元素的值和索引进行比较,如果元素的值不相等,则按值的降序排列,如果元素的值相等,则按索引的降序排列。
接下来,我们遍历数组 nums 的前 k 个元素,并将它们添加到优先队列 pq 中。每个元素都是一个数组,包含元素的值和索引。
new int[]{nums[i], i}是一个匿名整数数组对象的创建和初始化。它的作用是创建一个包含两个元素的整数数组,并将 nums[i] 赋值给数组的第一个元素,将 i 赋值给数组的第二个元素。
在这个特定的代码中,我们使用 new int[]{nums[i], i} 来创建一个包含当前元素值 nums[i] 和当前索引 i 的整数数组。然后,我们将这个数组添加到优先队列 pq 中,以便在后续的操作中使用。
然后,我们创建一个新的数组 ans,用于存储每个窗口的最大值。我们首先将优先队列 pq 中的最大元素的值存储在 ans 的第一个位置。
接下来,我们从第 k 个元素开始遍历数组 nums。对于每个元素,我们将其添加到优先队列 pq 中,并执行以下操作:
-
检查优先队列
pq的顶部元素(最大元素)的索引是否在当前窗口范围内。如果不在范围内,说明该元素已经不在当前窗口中,我们需要将其从优先队列pq中移除。我们反复执行此操作,直到顶部元素的索引在当前窗口范围内。 -
将优先队列
pq的顶部元素的值存储在ans数组中的相应位置。这个值就是当前窗口的最大值。
重复以上步骤,直到遍历完整个数组 nums。
最后,我们返回数组 ans,其中包含了每个窗口的最大值。
双端队列
这种方法就当是一个小扩展
第一种方法在每个窗口内通过遍历查找最大值,时间复杂度为 O(k)。可以使用双端队列(Deque) 来优化这个过程,将当前窗口内的较小元素从队列中移除,以保持队列的头部始终是窗口内的最大值的下标。这样可以将时间复杂度降低到 O(1)。
public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;if (n * k == 0) return new int[0];Deque<Integer> deque = new ArrayDeque<>();int[] maxList = new int[n - k + 1];for (int i = 0; i < nums.length; i++) {// 移除超出窗口范围的元素if (!deque.isEmpty() && deque.peek() < i - k + 1) {deque.poll();}// 移除窗口内小于当前元素的元素,保持队列头部始终是最大值while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {deque.pollLast();}//队列中加入数组的下标deque.offer(i);// 将窗口内的最大值存储在结果数组中if (i - k + 1 >= 0) {maxList[i - k + 1] = nums[deque.peek()];}}return maxList;
}
小码补充:
防止有人不了解Java中的双端队列,这里我们做一个简单的知识补充
在Java中,Deque 接口是双端队列(Double Ended Queue)的一种实现。Deque 具有队列和栈的性质,可以在队列的两端进行插入和删除操作。下面逐一解释 Deque 接口中的四个方法:poll()、peek()、peekLast() 和 offer()。
poll()方法用于检索并删除队列的头元素(首部元素)。如果队列为空,poll()方法将返回null。peek()方法用于检索队列的头元素(首部元素),但不删除它。如果队列为空,peek()方法将返回null。peekLast()方法用于检索队列的尾元素(尾部元素),但不删除它。如果队列为空,peekLast()方法将返回null。offer()方法用于在队列的尾部插入一个元素。如果队列已满,则offer()方法将返回false,否则返回true。
下面是这些方法的示例用法:
import java.util.*;
public class DequeExample {public static void main(String[] args) {Deque<Integer> deque = new ArrayDeque<>();// 添加元素到队列尾部deque.offer(1);deque.offer(2);deque.offer(3);System.out.println(deque); // 输出: [1, 2, 3]// 检索并删除队列头部元素int first = deque.poll();System.out.println(first); // 输出: 1System.out.println(deque); // 输出: [2, 3]// 检索队列头部元素但不删除int peeked = deque.peek();System.out.println(peeked); // 输出: 2// 检索队列尾部元素但不删除int peekedLast = deque.peekLast();System.out.println(peekedLast); // 输出: 3}
}
总结:
Deque接口中的poll()、peek()、peekLast()和offer()方法分别用于检索和操作双端队列的元素。poll()方法从队列头部检索并删除元素,peek()方法从队列头部检索元素但不删除,peekLast()方法从队列尾部检索元素但不删除,offer()方法将元素插入到队列尾部。
END
说实话,还是很有难度的,那个滑动窗口和堆的配合我也是想了半天才搞懂,不就是力扣上的难度题目,我没事😎🤏🕶 -> 😭 。
相关文章:
)
算法通关村第十六关黄金挑战——求滑动窗口中的最大值(滑动窗口与堆方法、双端队列法和直接比较法)
大家好,我是怒码少年小码。 今天这篇就讲一道题目,不难😎,但是一定要学会自己思考。 滑动窗口最大值 LeetCode 239:给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。…...

常见树种(贵州省):009楠木、樟木、桂木种类
摘要:本专栏树种介绍图片来源于PPBC中国植物图像库(下附网址),本文整理仅做交流学习使用,同时便于查找,如有侵权请联系删除。 图片网址:PPBC中国植物图像库——最大的植物分类图片库 一、楠木 …...
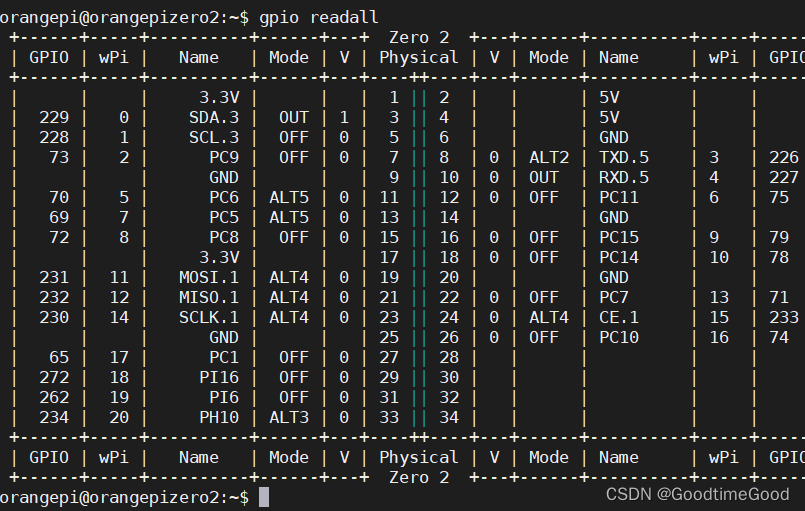
全志H616开发版
开发板介绍: 二、开发板刷机 SDFormatter TF卡的格式化工具、Win32Diskimager 刷机工具 刷机镜像为:Orangepizero2_2.2.0_ubuntu_bionic_desktop_linux4.9.170.img 使用MobaXterm_Personal_20.3连接使用 网络配置:nmcli dev wifi 命令接入网…...
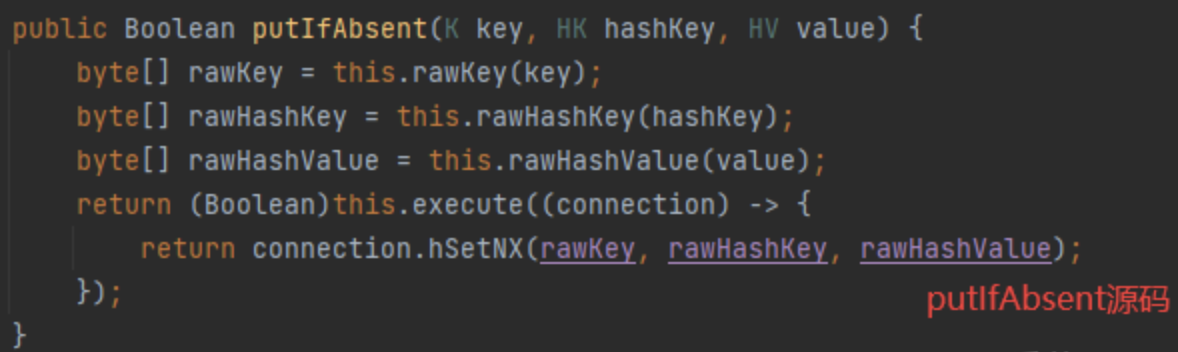
【Spring boot】RedisTemplate中String、Hash、List设置过期时间
文章目录 前言Redis中String设置时间的方法Redis中Hash和List设置时间的方法Redis中Hash的put、putAll、putIfAbsent区别 前言 时间类型:TimeUnit import java.util.concurrent.TimeUnit;TimeUnit.SECONDS:秒 TimeUnit.MINUTES:分 TimeUnit.HOURS&…...
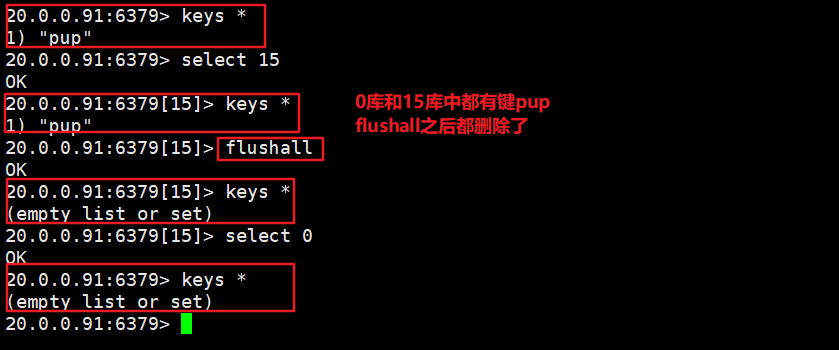
Nosql之redis概述及基本操作
关系数据库与非关系型数据库概述 关系型数据库 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一般面向于记录。SQL语句(标准数据查询语言)就是一种基于关系型数据库的语言,用于执行对关系型…...

使ros1和ros2的bag一直互通
很多文章都是先source ros1 然后source ros2,再play bag source /opt/ros/noetic/setup.bash source /opt/ros/foxy/setup.bash ros2 bag play -s rosbag_v2 kitti_raw00.bag 但实测会出问题: 为使ros1和ros2的bag一直互通 sudo apt update sudo apt install ros-foxy-ro…...

【正点原子 linux 驱动编程】
在此声明,正用点编的说明书真的拉,丝毫不具备兼容性。。比如linux的第一个实验,其中包含的 unregister_chrdev_region 函数,fileoperation 结构体等均来自 <linux/fs.h> 文件,搞不懂,他们方ide.h&…...

使用Python的turtle模块绘制玫瑰花图案(含详细Python代码与注释)
1.1引言 turtle模块是Python的标准库之一,它提供了一个绘图板,让我们可以在屏幕上绘制各种图形。通过使用turtle,我们可以创建花朵、叶子、复杂的图案等等。本博客将介绍如何使用turtle模块实现绘制图形的过程,并展示最终结果。 …...

Redis学习笔记14:基于spring data redis及lua脚本ZSET有序集合实现环形结构案例及lua脚本如何发送到redis服务器
案例实现目标,一、实现一个环形结构,环形结构上节点有一个阀值threshold,超过阀值则移除分数score最低的成员,不足则将当前成员添加进环中,且确保成员不可重复;二、每次访问环中的数据都需要刷新key的过期时间…...

openssl C++研发之pem格式处理详解
一、PEM_writeXXX和EM_write_bio_XXX 在OpenSSL的crypto/pem.h头文件中,PEM_write_XXXX和PEM_write_bio_XXXX系列函数用于将特定类型的数据写入文件或BIO(内存缓冲区)中,其中XXXX代表不同的数据类型。 这些函数的使用方式相似&a…...

【教3妹学编辑-mysql】详解数据库三大范式
什么是范式 简单地理解就是:数据库设计时遵循的规范 三大范式 数据库三大范式包含:1、第一范式(1NF);2、第二范式(2NF);3、第三范式(3NF)。其中,第一范式(1NF)的要求是属性不可分割,第二范式(2NF)的要求是…...

【计算机网络笔记】路由算法之链路状态路由算法
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...
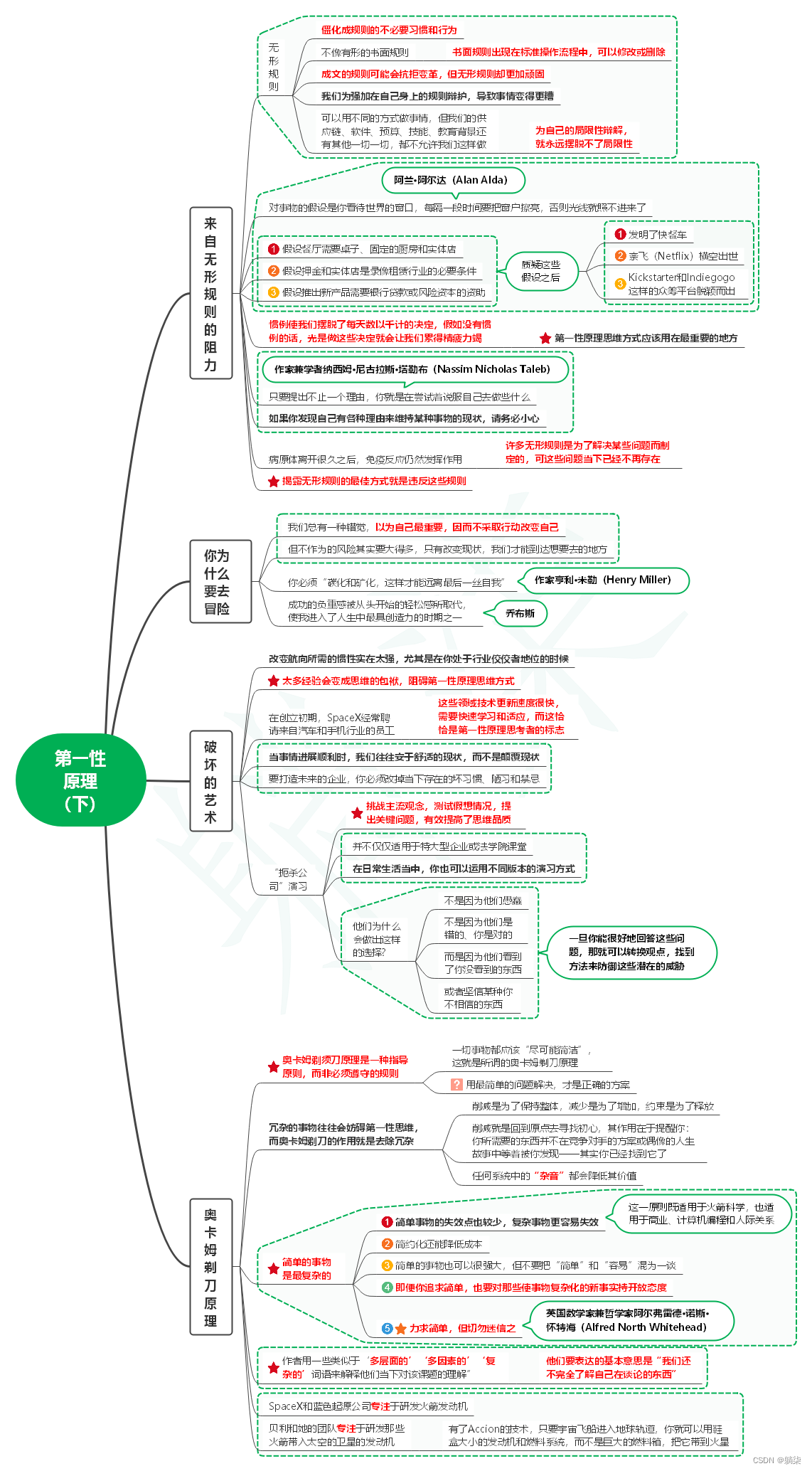
读像火箭科学家一样思考笔记04_第一性原理(下)
1. 来自无形规则的阻力 1.1. 无形规则 1.1.1. 僵化成规则的不必要习惯和行为 1.1.2. 不像有形的书面规则 1.1.2.1. 书面规则出现在标准操作流程中,可以修改或删除 1.1.3. 成文的规则可能会抗拒变革,但无形规则却更加顽固 1.1.4. 我们为强加在自己身…...

开源集群管理系统对比分析:Kubernetes 与 Apache Mesos
集群管理系统是关键的软件解决方案,可以在互连机器网络中有效分配和利用计算资源。毫无疑问,它们通过确保可扩展性、高可用性和有效的资源管理在现代计算中发挥着至关重要的作用,这使得它们对于运行复杂的应用程序、管理数据中心以及进一步增…...

matlab 坡度滤波算法地面分割
目录 一、算法原理1、实现流程2、参考文献二、代码实现三、结果展示四、测试数据一、算法原理 1、实现流程 1、格网示意图 2、计算格网行列数 公式中的特殊符号为向上取整,...

【腾讯云 HAI域探秘】高性能服务器引领AI革新浪潮:从AI绘画、知识问答到PyTorch图像分类、视频检测的全方位探索
目录 1 HAI(高性能应用服务)简介2 HAI的应用场景2.1 HAI在AI作画中的灵活性与效率2.2 深入探索LLM语言模型的应用与性能2.3 HAI支持的AI模型开发环境与工具 3 基于stable difussio的AI 绘画应用实践3.1 使用AI模型中的stable diffusion模型服务3.2 设置和…...
)
【Java】ExcelWriter自适应宽度工具类(支持中文)
工具类 import org.apache.poi.ss.usermodel.Cell; import org.apache.poi.ss.usermodel.CellType; import org.apache.poi.ss.usermodel.Row; import org.apache.poi.ss.usermodel.Sheet;/*** Excel工具类** author xiaoming* date 2023/11/17 10:40*/ public class ExcelUti…...

C++二分查找算法:132模式枚举3简洁版
本文涉及的基础知识点 二分查找算法合集 本题不同解法 包括题目及代码C二分查找算法:132 模式解法一枚举3C二分查找算法:132 模式解法二枚举2代码简洁C二分查找算法:132 模式解法三枚举1性能最佳C单调向量算法:132 模式解法三枚…...

Map 和 WeakMap:JavaScript 中的键值对集合
JavaScript 是一种动态、弱类型的脚本语言,经常用于构建现代 Web 应用程序。在编写 JavaScript 代码时,我们经常需要使用各种数据结构来存储和管理数据。其中,Map 和 WeakMap 就是两个非常有用的数据结构,它们分别提供了用于存储键…...
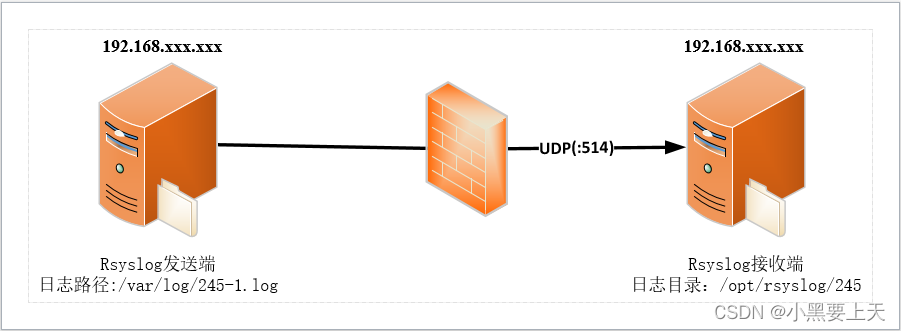
linux rsyslog综合实战1
本次我们通过rsyslog服务将A节点服务器上的单个日志(Path:/var/log/245-1.log)实时同步到B节点服务器目录下(Path:/opt/rsyslog/245) 1.rsyslog架构 2.环境信息 环境信息 HostnameIpAddressOS versionModuleNotersyslog1192.168.10.245CentOS Linux release 7.9.2009 (Core)rs…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
