2023年中国醇酸树脂涂料需求量、应用领域及市场规模前景分析[图]
醇酸树脂指多元醇和多元酸与脂肪酸经过酯化缩聚生成的高聚物,其由邻苯二甲酸酐、多元醇和脂肪酸或甘油三脂肪酸酯缩合聚合而成。醇酸树脂固化成膜后,具有耐磨性好、绝缘性佳等优势,在涂料领域应用广泛。2022年醇酸树脂产量约336.3万吨,需求量336.64万吨
2011-2022年中国醇酸树脂产销量
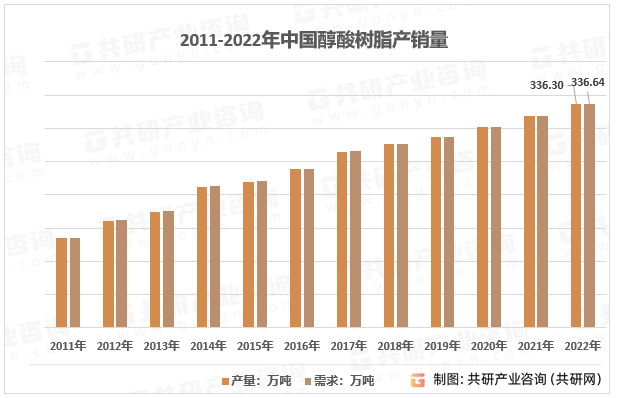
资料来源:共研产业咨询(共研网)
醇酸树脂涂料具有更强的粘合力、耐湿性、不易燃和防腐蚀等优势,因此被用于某些海洋应用领域,例如船体和甲板、桥梁、钢铁、储罐和木材。此外,近年来世界海上贸易的增加、海上航行的增加、对安全自动化系统的需求增加以及海上旅游业的增加正在促进海洋工业的发展。在市场需求带动下,我国醇酸树脂涂料需求将不断提升。2022年我国涂料树脂需求总量为1220.8万吨,涂料用醇酸树脂需求量为264.6万吨。
2016-2022年中国涂料用醇酸树脂需求量
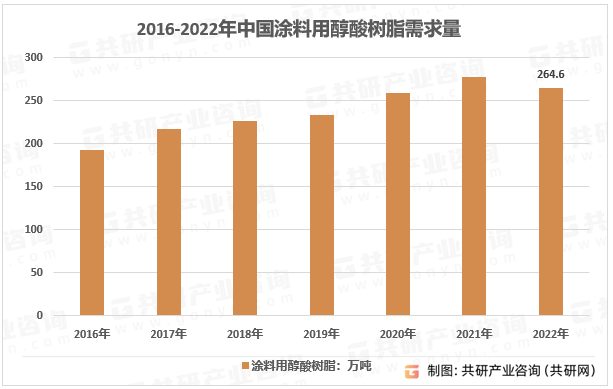
资料来源:共研产业咨询(共研网)
生物基材料是我国战略性新兴产业的重要方向,对于抢占新一轮科技革命和产业革命制高点,加快壮大新产业、培育新动能,支撑我国“双碳”战略,推动产业升级具有重要战略和现实的意义。在涂料应用领域,生物基材料特别是植物油已经广泛地用于制备新型的绿色环保涂料,特别是醇酸树脂涂料。醇酸树脂涂料作为应用范围最广的树脂涂料之一,市场前景广阔,2022年醇酸树脂涂料市场规模297.41亿元。
2016-2023年中国醇酸树脂涂料市场规模及预测
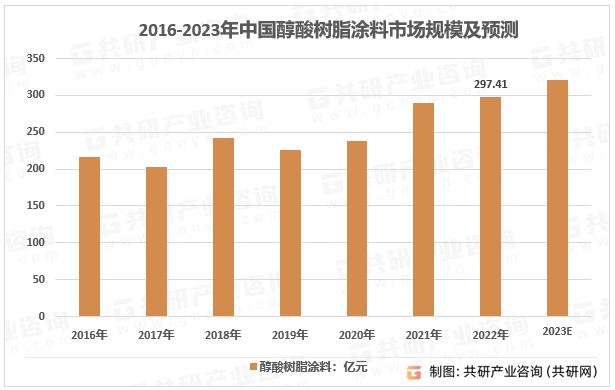
资料来源:共研产业咨询(共研网)
相关文章:

2023年中国醇酸树脂涂料需求量、应用领域及市场规模前景分析[图]
醇酸树脂指多元醇和多元酸与脂肪酸经过酯化缩聚生成的高聚物,其由邻苯二甲酸酐、多元醇和脂肪酸或甘油三脂肪酸酯缩合聚合而成。醇酸树脂固化成膜后,具有耐磨性好、绝缘性佳等优势,在涂料领域应用广泛。2022年醇酸树脂产量约336.3万吨&#x…...
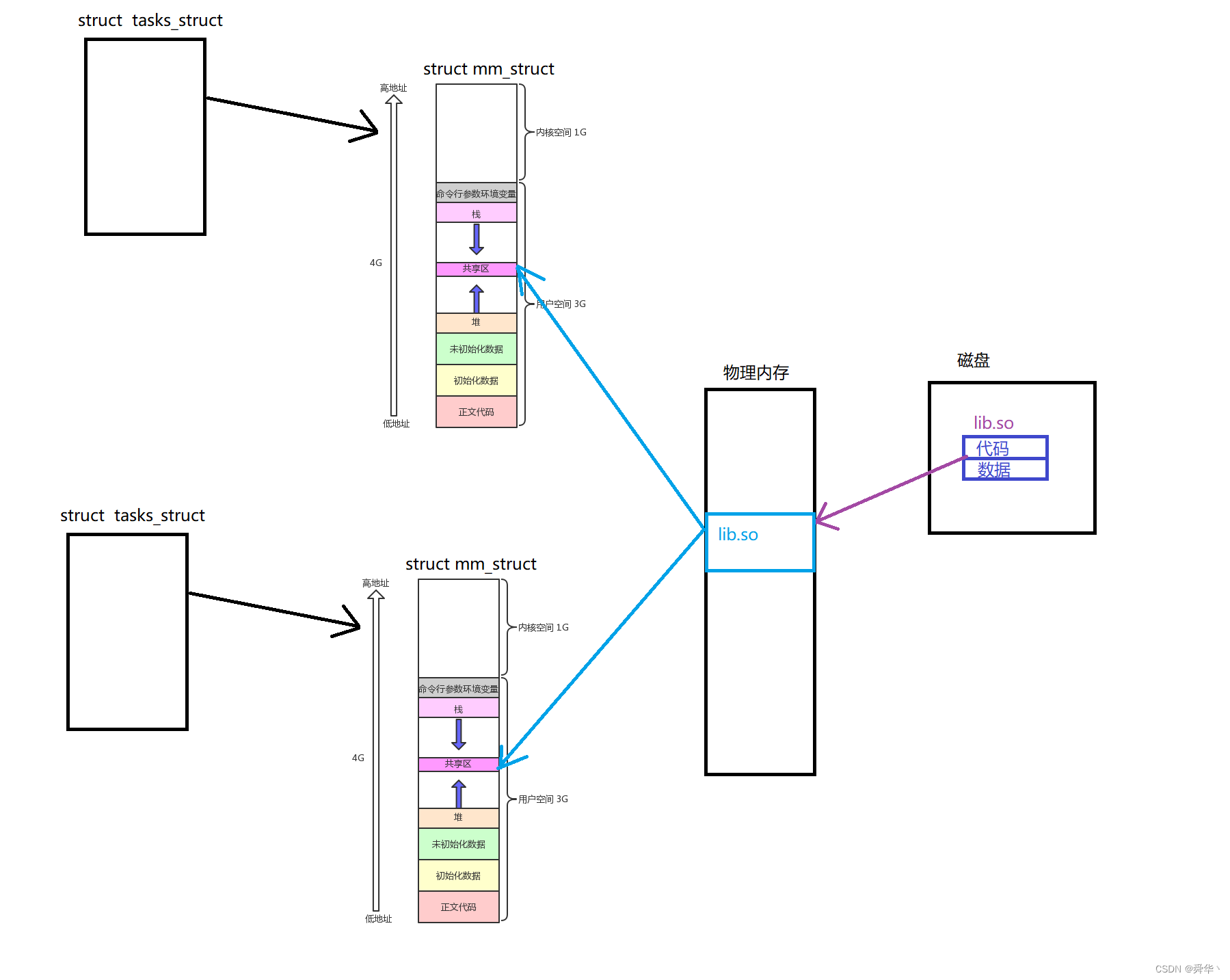
【Linux进阶之路】动静态库
文章目录 回顾一. 静态库1.代码传递的方式2.简易制作3.原理 二. 动态库1.简易制作2.基本原理 尾序 回顾 前面在gcc与g的使用中,我们简单的介绍了动态库与静态库的各自的优点与区别: 动态链接库,也就是所有的程序公用一份代码,虽然方便省空间&…...

Ubuntu磁盘扩展容量
gparted扩展...
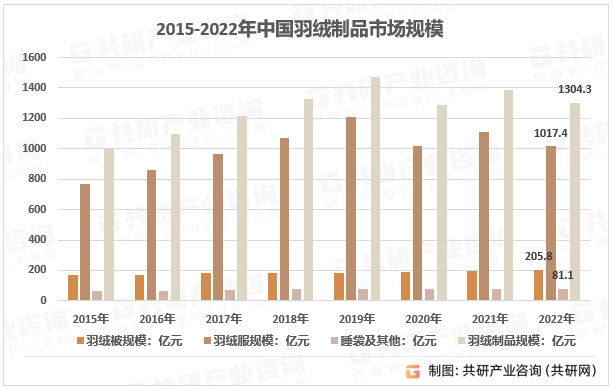
2023年中国羽绒制品需求现状、市场规模及细分产品规模分析[图]
羽绒羽毛指生长在水禽类动物(鹅、鸭)腋下、腹部羽绒和羽毛的统称,属于上游鹅鸭肉食品工业副产品的综合利用,是下游羽绒制品的填充料。根据国家标准,绒子含量≥50%的称为羽绒,绒子含量<50%的称为…...
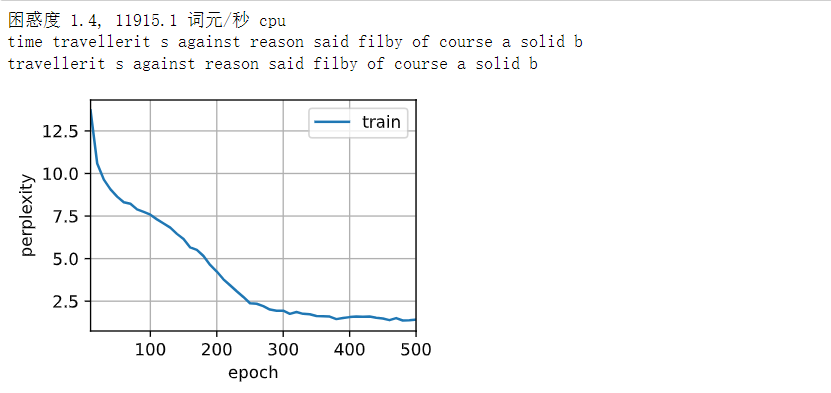
动手学深度学习——循环神经网络的从零开始实现(原理解释+代码详解)
文章目录 循环神经网络的从零开始实现1. 独热编码2. 初始化模型参数3. 循环神经网络模型4. 预测5. 梯度裁剪6. 训练 循环神经网络的从零开始实现 从头开始基于循环神经网络实现字符级语言模型。 # 读取数据集 %matplotlib inline import math import torchfrom torch import …...

【操作系统】文件系统的逻辑结构与目录结构
文章目录 文件的概念定义属性基本操作 文件的结构文件的逻辑结构文件的目录结构文件控制块(FCB)索引节点目录结构 文件的概念 定义 在操作系统中,文件被定义为:以计算机硬盘为载体的存储在计算机上的信息集合。 属性 描述文件…...
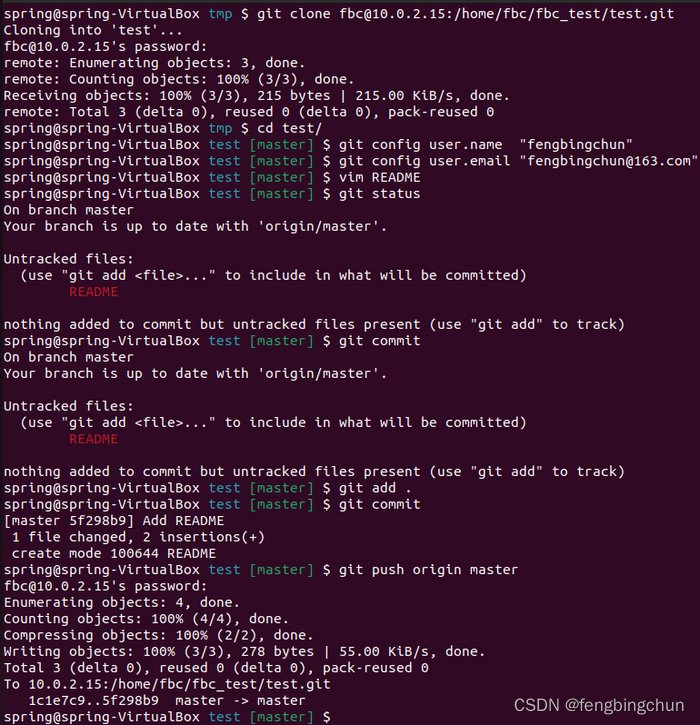
局域网内Ubuntu上搭建Git服务器
1.在局域网内选定一台Ubuntu电脑作为Git服务端: (1).新建用户如为fbc,执行如下命令:需设置密码,此为fbc sudo adduser fbc (2).切换到fbc用户:需密码,此前设置为fbc su fbc (3).建一个空目录作为仓…...

基础课10——自然语言生成
自然语言生成是让计算机自动或半自动地生成自然语言的文本。这个领域涉及到自然语言处理、语言学、计算机科学等多个领域的知识。 1.简介 自然语言生成系统可以分为基于规则的方法和基于统计的方法两大类。基于规则的方法主要依靠专家知识库和语言学规则来生成文本࿰…...

xpath
xpath 使用 使用 from lxml import etree或者 from lxml import htmlet etree.XML(xml) et etree.HTML(html) res et.xpath("/book") # 返回列表项目Valueet.xpath(“/book”)/表示根节点/div/a子节点用/依次表示/name/text()text()取文本/book//nick//表示标签…...
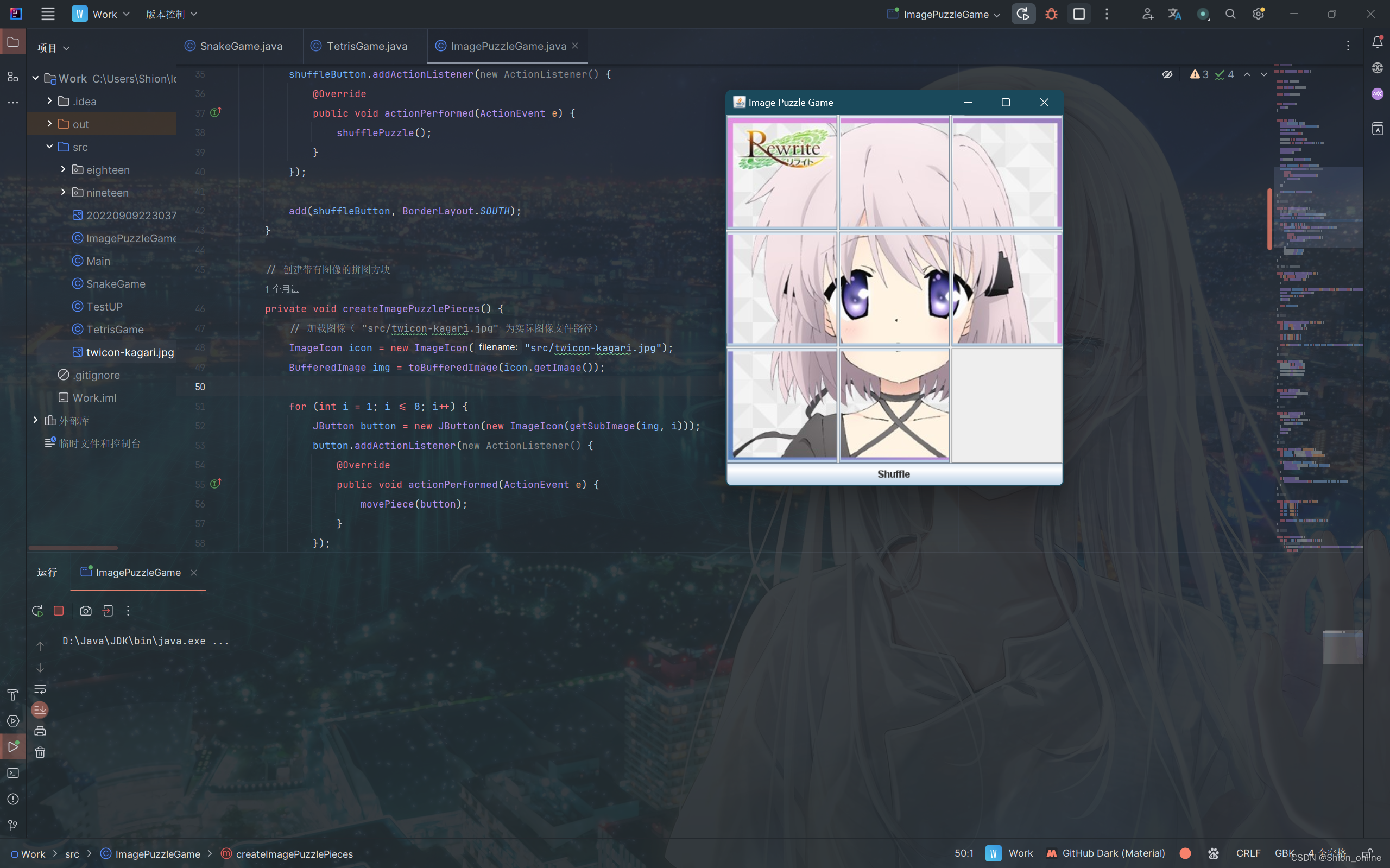
Java拼图小游戏
Java拼图小游戏 import javax.swing.*; import java.awt.*; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.image.BufferedImage; import java.util.ArrayList; import java.util.Collections; import java.util.List;public cla…...

终于有人把数据资产入表知识地图总结出来了,轻松看懂
在当前数字化的浪潮下,数据已经成为劳动、土地、知识、技术以后的第五大生产要素,“数据就是资源”已成为共识。如今数据资产“入表”已成定局,数据资产化迫在眉睫。 2023年8月21日,财政部正式印发《企业数据资源相关会计处理暂行…...
白鳝:聊聊IvorySQL的Oracle兼容技术细节与实现原理
两年前听瀚高的一个朋友说他们要做一个开源数据库项目,基于PostgreSQL,主打与Oracle的兼容性,并且与PG社区版内核同步发布。当时我听了有点不太相信,瀚高的Highgo是在PG内核上增加了一定的Oracle兼容性的特性,一般也会…...
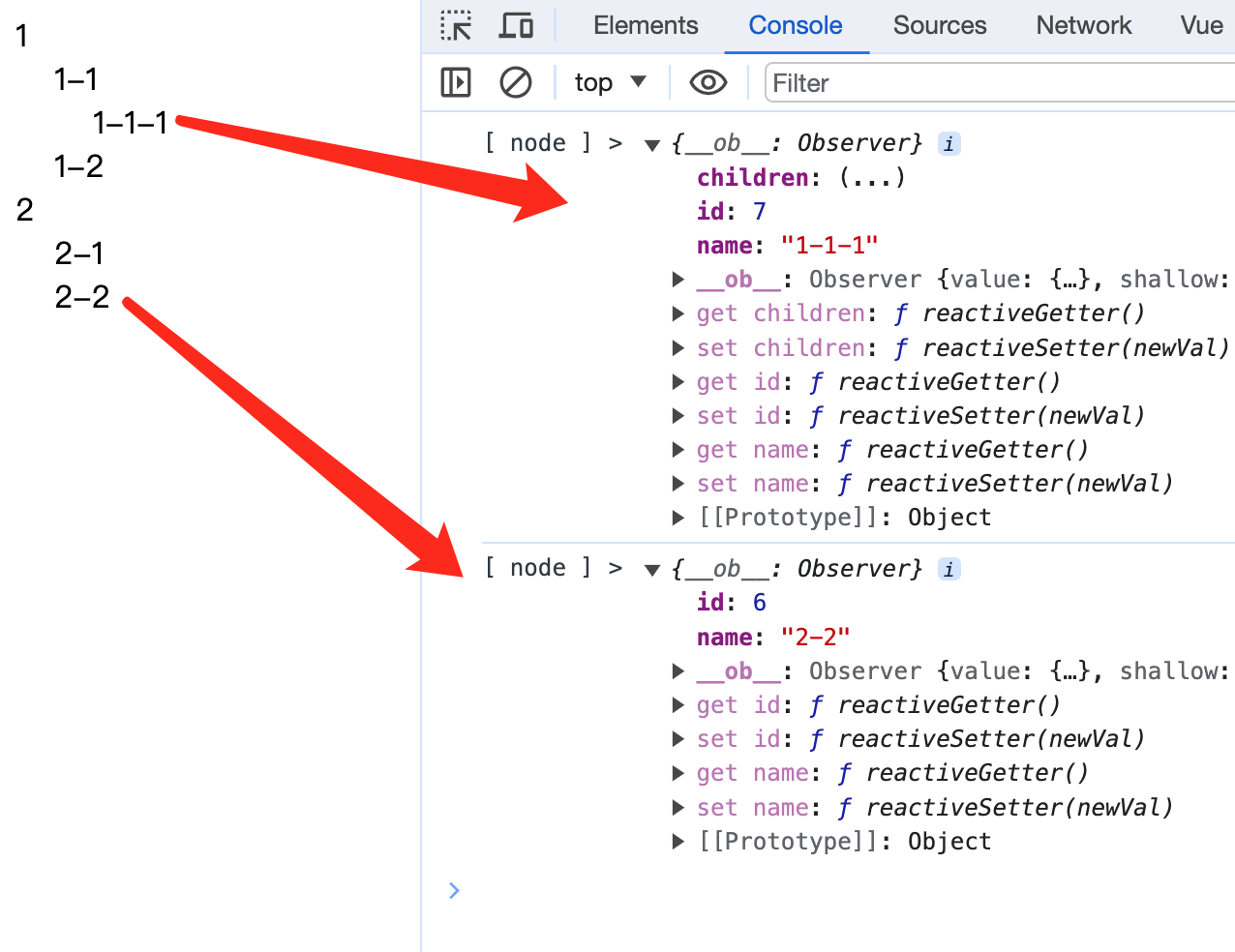
vue和uni-app的递归组件排坑
有这样一个数组数据,实际可能有很多级。 tree: [{id: 1,name: 1,children: [{ id: 2, name: 1-1, children: [{id: 7, name: 1-1-1,children: []}]},{ id: 3, name: 1-2 }]},{id: 4,name: 2,children: [{ id: 5, name: 2-1 },{ id: 6, name: 2-2 }]} ]要渲染为下面…...

【考研】数据结构(更新到顺序表)
声明:所有代码都可以运行,可以直接粘贴运行(只有库函数没有声明) 线性表的定义和基本操作 基本操作 定义 静态: #include<stdio.h> #include<stdlib.h>#define MaxSize 10//静态 typedef struct{int d…...

汇编-指针
一个变量如果包含的是另一个变量的地址, 则该变量就称为指针(pointer) 。指针是操作数组和数据结构的极好工具,因为它包含的地址在运行时是可以修改的。 .data arrayB byte 10h, 20h, 30h, 40h ptrB dword arrayB ptrB1 dword OFFSET arrayBarray…...

常见Web安全
一.Web安全概述 以下是百度百科对于web安全的解释: Web安全,计算机术语,随着Web2.0、社交网络、微博等等一系列新型的互联网产品的诞生,基于Web环境的互联网应用越来越广泛,企业信息化的过程中各种应用都架设在Web平台…...

milvus数据库搜索
一、向量相似度搜索 在Milvus中进行向量相似度搜索时,会计算查询向量和集合中具有指定相似性度量的向量之间的距离,并返回最相似的结果。通过指定一个布尔表达式来过滤标量字段或主键字段,您可以执行混合搜索。 1.加载集合 执行操作的前提是…...

HEVC参考帧技术
为了增强参考帧管理的抗差错能力,HEVC采用了参考帧集技术,通过直接在每一帧的片头码流中传输DPB中各个帧的状态变化,将当前帧以及后续帧可能用到的参考帧在DPB中都进行描述,描述以POC作为一帧的身份标识。因此,不需要依…...

QT小记:The QColor ctor taking ints is cheaper than the one taking string literals
这个警告意味着在使用 Qt 的 C 代码中,使用接受整数参数的 QColor 构造函数比使用接受字符串字面值的构造函数更有效率。 要解决这个警告,你可以修改你的代码,尽可能使用接受整数参数的 QColor 构造函数,而不是字符串字面值。例如…...

机器人走迷宫问题
题目 1.房间有XY的方格组成,例如下图为64的大小。每一个方格以坐标(x,y) 描述。 2.机器人固定从方格(0, 0)出发,只能向东或者向北前进,出口固定为房间的最东北角,如下图的 方格(5,3)。用例保证机器人可以从入口走到出口。 3.房间…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
