C++刷题 -- 二分查找
C++刷题 – 二分查找
文章目录
- C++刷题 -- 二分查找
- 一、原理
- 二、例题
- 1.二分查找
- 2.使用二分查找确定target左右边界
- 3.x的平方根
一、原理
条件:数组为有序数组,数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的;
- 第一种写法:

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2if (nums[middle] > target) {right = middle - 1; // target 在左区间,所以[left, middle - 1]} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,所以[middle + 1, right]} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};
- 第二种写法:

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <int middle = left + ((right - left) >> 1);if (nums[middle] > target) {right = middle; // target 在左区间,在[left, middle)中} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,在[middle + 1, right)中} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};
二、例题
1.二分查找
https://leetcode.cn/problems/binary-search/description/
2.使用二分查找确定target左右边界
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/
- 该题目的要点在于非递减数组(升序,但是有可能有重复数字)中寻找target的左右边界,target可能有多个重复值的情况;
- 时间复杂度需要是O(log N),表明需要使用二分查找确定左右边界,不能采用遍历方法确定边界;
- 先确定情况:
- target不再nums区间内;
- target在nums区间内,但是nums中没有target;
- nums中有target;
使用二分查找确定边界的原理:
二分查找在没有查找到target的时候,target是在最终的(left, right)这个区间之内的,可以使用这个原理来分别找出左右边界;
- 确定右边界

当nums[mid]的值小于等于target的时候,选择更新right_border,right_border需要跟着left更新,因为无论是否找到target,最终left一定会指向nums中大于target的数中最小的那个数,就是target的有边界(开区间); - 左边界同理;
特殊情况:
- nums为{2, 2},target为3,最终左右边界输出值为(-2, 2),之间的差值大于1,应该输出左右边界,但是target却不在nums中;
解决方案:直接在最外面加一个判断target是否属于nums区间的条件;
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {vector<int> res;int tar_l = leftBorder(nums, target);int tar_r = rightBorder(nums, target);cout << tar_l << " " << tar_r << endl;if(nums.empty() || (target < nums[0] || target > nums[nums.size() - 1])){//target不在nums范围res.push_back(-1);res.push_back(-1);}else if(tar_r - tar_l > 1){//target存在于nums中res.push_back(tar_l + 1);res.push_back(tar_r - 1);}else{//target不存在于nums中res.push_back(-1);res.push_back(-1);}return res;}//寻找右边界 -- target右边的一个位置int rightBorder(vector<int>& nums, int target){int right_border = -2;int left = 0, right = nums.size() - 1;//进行二分查找while(left <= right){int mid = left + ((right - left) / 2);if(nums[mid] > target)//不断缩小右边界{right = mid - 1;}else{//缩小左边界//且当找到target时,left继续向右,目的是找到最右边target的位置left = mid + 1;right_border = left;//left最终指向的会是nums中大于target的最小数}} return right_border;}//寻找左边界int leftBorder(vector<int>& nums, int target){int left_border = -2;int left = 0, right = nums.size() - 1;//进行二分查找while(left <= right){int mid = left + ((right - left) / 2);if(nums[mid] < target)//不断缩小左边界{left = mid + 1;}else{//缩小右边界//且当找到target时,right继续向右,目的是找到最左边target的位置right = mid - 1;left_border = right;//right最终指向的会是nums中小于target的最大数}} return left_border;}};
3.x的平方根
https://leetcode.cn/problems/sqrtx/submissions/483798269/
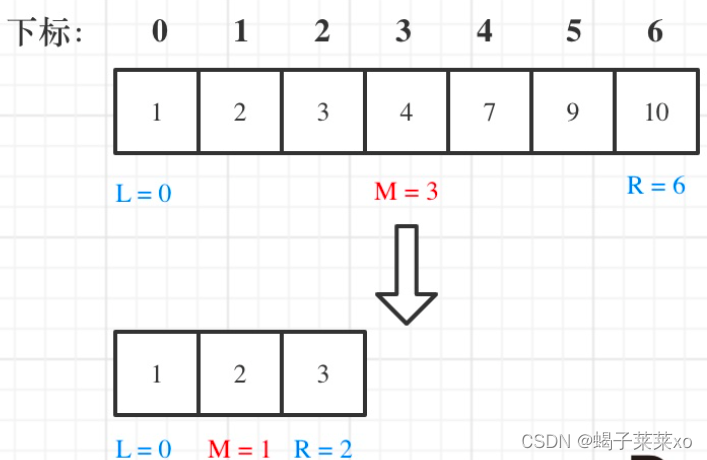
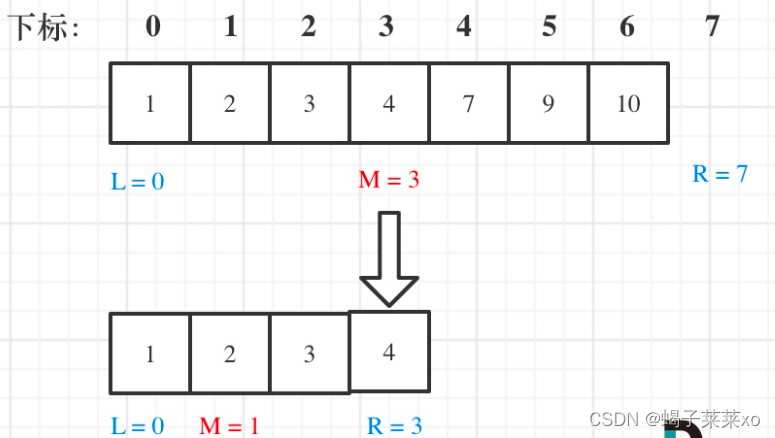
从题目的要求和示例我们可以看出,这其实是一个查找整数的问题,并且这个整数是有范围的。
- 如果这个整数的平方 恰好等于 输入整数,那么我们就找到了这个整数;
- 如果这个整数的平方 严格大于 输入整数,那么这个整数肯定不是我们要找的那个数;
- 如果这个整数的平方 严格小于 输入整数,那么这个整数 可能 是我们要找的那个数(重点理解这句话)。
因此我们可以使用「二分查找」来查找这个整数,不断缩小范围去猜。
方法一:
- 猜的数平方以后大了就往小了猜;
- 猜的数平方以后恰恰好等于输入的数就找到了;
- 猜的数平方以后小了,可能猜的数就是,也可能不是。
class Solution {
public:int mySqrt(int x) {int min = 0, max = x;int res = 0;while(min <= max){int mid = min + (max - min) / 2;if((long long)mid * mid <= x) // 防止乘法溢出{// 目标结果的平方小于等于x,寻找出的就是范围内最大的满足平方<=x的数min = mid + 1;res = mid;}else{max = mid - 1;}}return res;}
};
方法二:
- 使用二分查找寻找边界,目标数其实就是左边界;
class Solution {
public:int mySqrt(int x) {int min = 0, max = x;int res = 0;//寻找左边界while(min <= max){int mid = min + ((max - min) / 2);if((long long)mid * mid < x){min = mid + 1;}else if((long long)mid * mid > x){max = mid - 1;res = max;}else{return mid;}}return res;}
};
相关文章:

C++刷题 -- 二分查找
C刷题 – 二分查找 文章目录 C刷题 -- 二分查找一、原理二、例题1.二分查找2.使用二分查找确定target左右边界3.x的平方根 一、原理 条件:数组为有序数组,数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能…...
PHPmail 发送邮件错误 550 的原因是什么?
电子邮件错误消息链接到简单邮件传输协议 (SMTP),这是一组发送和接收电子邮件的标准化规则。因此,它也称为 SMTP 550 错误代码。在某些情况下,电子邮件错误 550 是由收件人一方的问题引起的。 以下是电子邮件错误 550 的一些可能原因&#x…...

数字化转型导师坚鹏:数字化时代银行网点厅堂营销5大难点分析
数字化时代银行网点厅堂营销存在以下5大难点: 1、识别难。识别有效的客户比较难,传统的厅堂识别主要依据客户的衣着气质等主管感受,判断客户是否为潜在中高端客户,提供相关服务。大堂经理主管识别与智能化系统识别相结合…...
www.testfire.nets渗透测试报告
www.testfire.nets渗透测试报告 一、测试综述 1.1.测试⽬的 通过实施针对性的渗透测试,发现testfire.net⽹站的安全漏洞,锻炼自己的渗透水平 1.2.测试范围 域名:www.testfire.net IP:65.61.137.117 测试时间: 2023年11月…...

多模态大一统:通向全模态学习和通用人工智能的未来之路
随着AI技术的不断发展,研究者们正试图构建一种真正通用的人工智能,它能像人们那样以统一的方式处理和理解多种模态的信息。多模态大一统是这一愿景的关键,它旨在开启全模态LLM(深度学习语言模型)和通用AI时代的大门。在…...

实用篇-ES-DSL查询文档
数据的存储不是目的,我们希望从海量的酒店数据中检索出需要的信息,这就是ES的搜索功能 官方文档: https://elastic.co/guide/en/elasticsearch/reference/current/query-dsl.html#query-dsl。DSL是用来查询文档的 Elasticsearch提供了基于JSON的DSL来定…...
Nacos配置管理
将配置交给Nacos管理的步骤 1、在Nacos中添加配置文件 2、在微服务中引入nacos的config依赖 3、在微服务中添加bootstrap.yml,配置nacos地址、当前环境、服务名称、文件后缀名。这些决定了程序启动时去nacos读取哪个文件 Nacos配置更改后,微服务可以实…...
【前端学java】Java中的异常处理(15)完结
往期回顾: 【前端学java】JAVA开发的依赖安装与环境配置 (0)【前端学java】java的基础语法(1)【前端学java】JAVA中的packge与import(2)【前端学java】面向对象编程基础-类的使用 (…...

深入理解MySQL存储引擎、InnoDB与MyISAM的比较以及事务处理机制
介绍 MySQL是一款强大而灵活的关系型数据库管理系统,它支持多种存储引擎,每个引擎都有其独特的特点和适用场景。在本篇博客中,我们将深入探讨MySQL存储引擎的种类、InnoDB与MyISAM的区别,以及事务的概念及其在MySQL中的实现方式。…...

webpack 中,filename 和 chunkFilename 的区别
filename filename 是一个很常见的配置,就是对应于 entry 里面的输入文件,经过webpack打包后输出文件的文件名。比如说经过下面的配置,生成出来的文件名为 index.min.js。 chunkFilename chunkFilename 指未被列在 entry 中,却…...
gitlab 实战
一.安装依赖 yum install -y curl policycoreutils-python openssh-server perl 二.安装gitlab yum install gitlab-jh-16.0.3-jh.0.el7.x86_64.rpm 三.修改下面的 vim /etc/gitlab/gitlab.rbexternal_url http://192.168.249.156 四.初始化 gitlab-ctl reconfigure 五.查看状…...

openGauss学习笔记-128 openGauss 数据库管理-设置透明数据加密(TDE)
文章目录 openGauss学习笔记-128 openGauss 数据库管理-设置透明数据加密(TDE)128.1 概述128.2 前提条件128.3 背景信息128.4 密钥管理机制128.5 表级加密方案128.6 创建加密表128.7 切换加密表加密开关128.8 对加密表进行密钥轮转 openGauss学习笔记-12…...

Redis从入门到精通(三)-高阶篇
文章目录 0. 前言[【高阶篇】3.1 Redis协议(RESP )详解](https://blog.csdn.net/wangshuai6707/article/details/132742584)[【高阶篇】3.3 Redis之底层数据结构简单动态字符串(SDS)详解](https://blog.csdn.net/wangshuai6707/article/details/131101404)[【高阶篇】3.4 Redis…...

线性表--队列-1
文章目录 主要内容一.队列基础练习题1.用链式存储方式的队列进行删除操作时需要 ( D ).代码如下(示例): 2.若以1,2,3,4作为双端队列的输入序列,则既不能由输入受限的双端队列得到,又不能由输出受限的双端队列得到的输出序列是( C …...

【开题报告】基于uni-app的汽车租赁app的设计与实现
1.项目背景及意义 项目背景: 随着人们生活水平的提高,汽车租赁服务在城市中变得越来越普及。传统的租车方式存在一些问题,比如租车流程繁琐、费用不透明、选择有限等。因此,开发一款基于uni-app的汽车租赁app成为了满足用户需求…...

Java实现围棋算法
围棋是一种源自中国的棋类游戏,也是世界上最古老、最复杂的棋类游戏之一。该游戏由黑白两方交替放置棋子在棋盘上进行,目的是将自己的棋子占据更多的空间,并将对手的棋子围死或吃掉,最终获得胜利。围棋不仅是一种游戏,…...
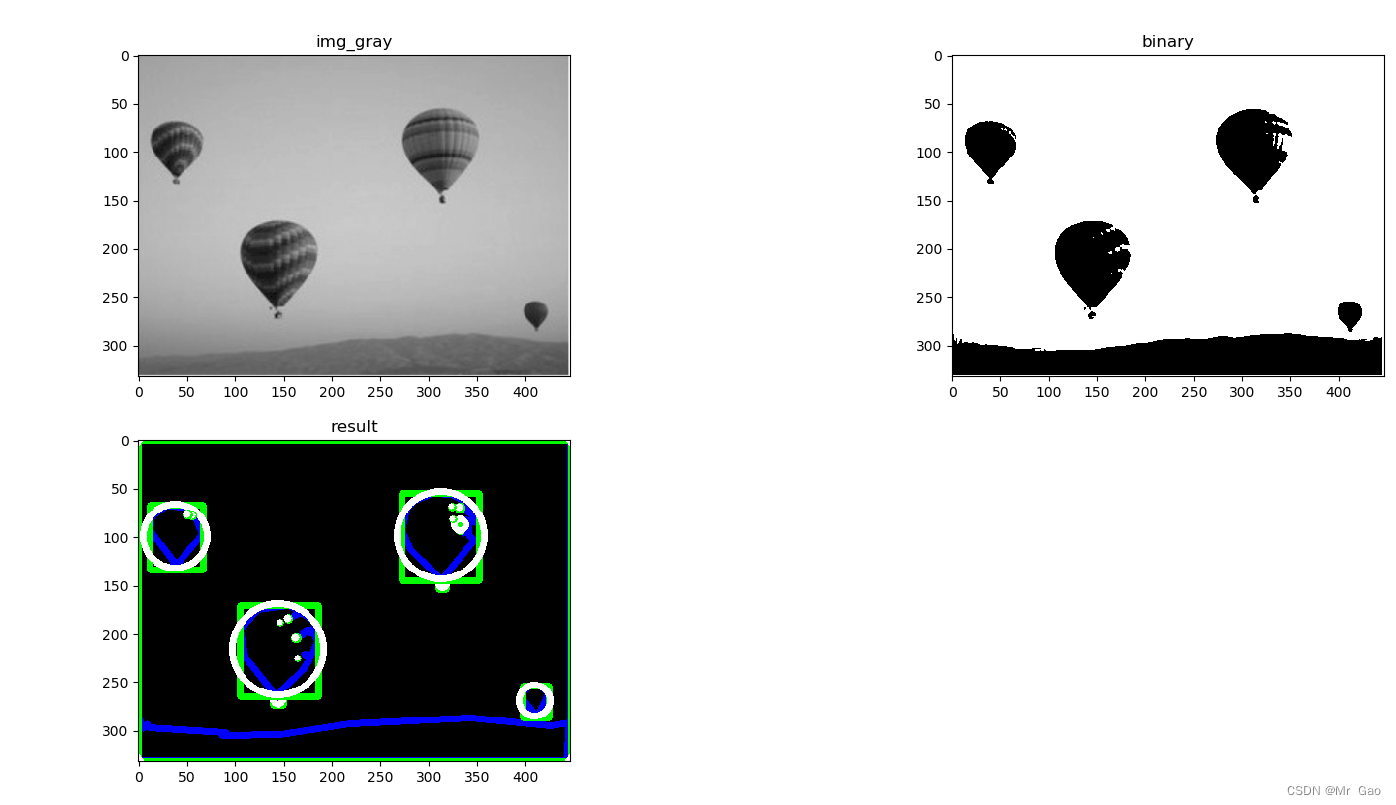
python -opencv 边缘检测
python -opencv 边缘检测 边缘检测步骤: 第一步:读取图像为灰度图 第二步:进行二值化处理 第三步:使用cv2.findContours对二值化图像提取轮廓 第三步:将轮廓绘制到图中 代码如下: from ctypes.wintypes import SIZ…...
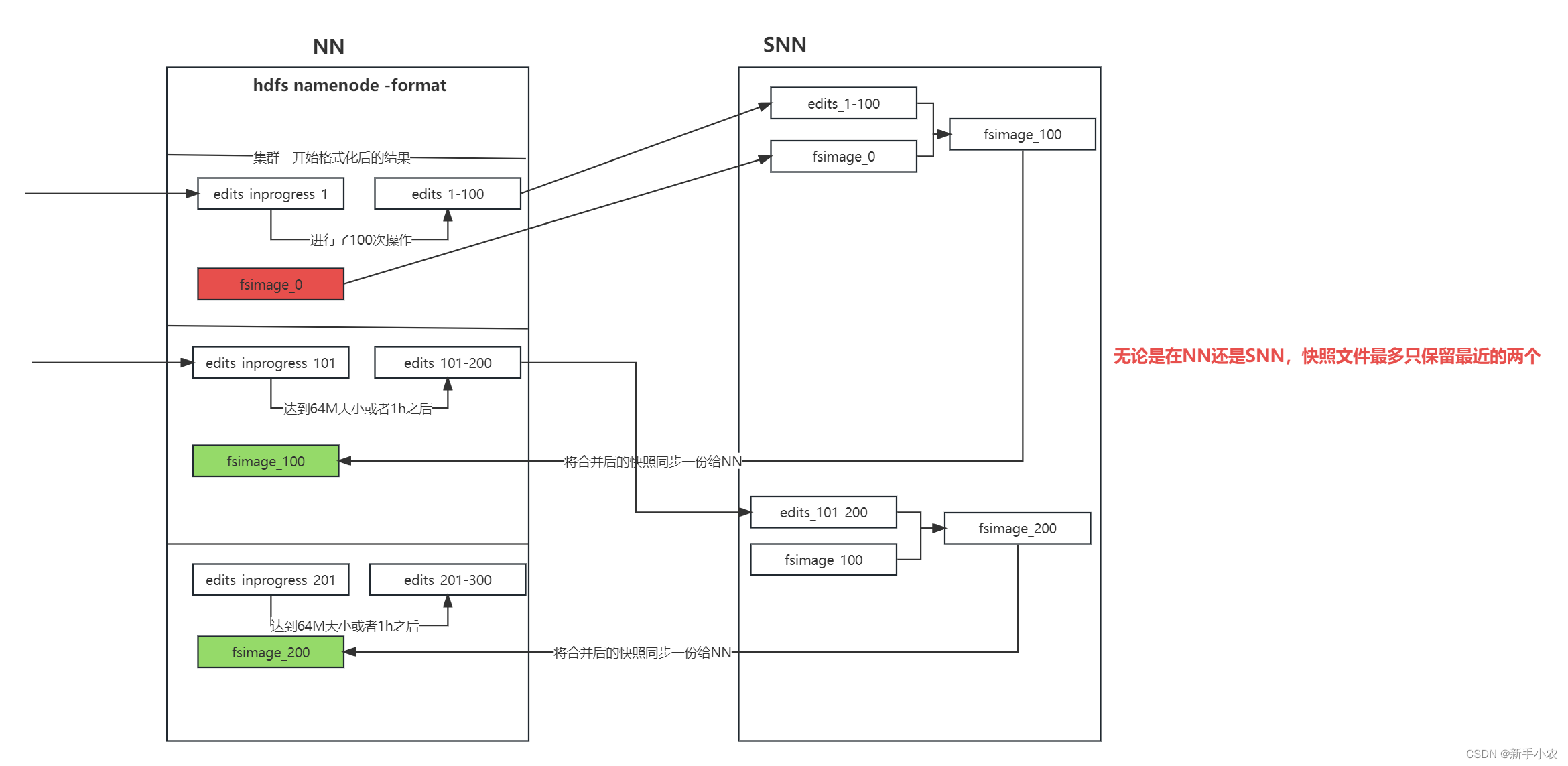
Hadoop-- hdfs
1、HDFS中的三个进程:NameNode(NN)、DataNode(DN)、SecondNameNode(SNN) 2、NameNode(NN) 1、作用: 1、接收客户端的一个读、写的服务,在namenode上存储了数据文件和datanode的映射的关系。 …...

《论文阅读》CAB:认知、情感和行为的共情对话生成 DASFAA 2023
《论文阅读》CAB:认知、情感和行为的共情对话生成 前言摘要相关知识CVAE 条件变分自编码器最大最小归一化模型架构1.获取 Representation2.Prior Network and Recognition Network (Affection)3.Knowledge Acquisition and Fusion (Cognition)4.Dialogue Act Predictor and Re…...
审计dvwa高难度命令执行漏洞的代码,编写实例说明如下函数的用法
审计dvwa高难度命令执行漏洞的代码 ,编写实例说明如下函数的用法 代码: <?phpif( isset( $_POST[ Submit ] ) ) {// Get input$target trim($_REQUEST[ ip ]);// Set blacklist$substitutions array(& > ,; > ,| > ,- > ,$ …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
