数学建模-图与网络模型解题方法和代码实现
本文针对以下几个方面问题进行整理:
- 最短路问题
- 两个指定顶点之间的最短路径
- 任意顶点之间的最短路径
2.最小生成树问题
- 求最小生成树
3.网络最大流问题
- 源点与汇点之间的最大流
- 基于最大流的最小费用求解
4.旅行商问题
- 基于哈密顿(Hamilton)圈求解旅行商线性规划
最短路问题:
两个指定点最小距离:
%使用graphshortestpath函数
[dist, path, pred]=graphshortestpath(G,S,T)G是稀疏矩阵,S是起点,T是终点。dist表示最短距离,path表示最短距离经过的路径节点,pred表示从S到每个节点的最短路径中,目标节点的先驱,即目标节点的前面一个节点。比如一共有6个点,S=1,那么运行这个函数后pred存的就是S=1这个节点到其它节点T'最短路径上T'的前一个节点。这个函数也就是求出图G上S到T的[dist, path, pred],当不写T时表示求S到其它所有点的[dist, path, pred]。
任意顶点的最短路径:
!使用graphallshortestpath函数
[dist] = graphallshortestpaths(G)- 解题思路:

简单构造稀疏矩阵:
- 手动录入权重矩阵
!w(起点,终点)=权重值
w=zeros(4)
w(1,2)=2;w(1,3)=3;w(1,4)=8;
w(2,3)=6;w(2,4)=6;
G=sparse(w);
%如果是无向图,G=sparse(tril(w'+w)取下三角)得:
G =
(1,2) 2
(1,3) 3
(2,3) 6
(1,4) 8
(2,4) 6
2. 直接sparse函数生成
%sparse([起点集合],[对应终点集合],[对应权重集合])
G=sparse([1,1,2,1,2],[2,3,3,4,4],[2,3,6,8,6]);
%得到结果和上面相同
%如果是无向图,建议用方法1对无向图而言:tril(w+w')是在不知道w是上三角还是下三角的情况下,确保取w对应的下三角;若w已知为上三角,稀疏矩阵G=sparse(w');若已知w为下三角,稀疏矩阵G=sparse(w);
例题:某公司在六个城市c1,c2,..c6中有分公司,从ci(1..6)到cj(1..6)的距离c(i,j)记在下述矩阵中,求ci到其他城市的最短距离。
| 0 | 50 | ∞ | 40 | 25 | 10 |
|---|---|---|---|---|---|
| 50 | 0 | 15 | 20 | ∞ | 25 |
| ∞ | 15 | 0 | 10 | 20 | ∞ |
| 40 | 20 | 10 | 0 | 10 | 25 |
| 25 | ∞ | 20 | 10 | 0 | 55 |
| 10 | 25 | ∞ | 25 | 55 | 0 |
clear;
clc;
w=zeros(6);
w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;
w(2,3)=15;w(2,4)=20;w(2,6)=25;
w(3,4)=10;w(3,5)=20;
w(4,5)=10;w(4,6)=25;
w(5,6)=55;
%无向图
G=sparse(w');
a=graphallshortestpaths(G,'Direct',0)
%记住要加Direct 0/false 说明是无向图 1/true则为有向图得:
a =
0 35 45 35 25 10
35 0 15 20 30 25
45 15 0 10 20 35
35 20 10 0 10 25
25 30 20 10 0 35
10 25 35 25 35 0
例如第一行表示c1到ci(1..6)最短距离分别为[0,35,45,35,25,10].
最小生成树问题
同样直接运用graphminspantree函数并加一些图形显示参数即可
例:北京(Pe)、东京(T)、纽约(N)、墨西哥城(M)、伦敦(L)、巴黎(Pa)各城市之间航线距离如下表
| L | M | N | Pa | Pe | T | |
|---|---|---|---|---|---|---|
| L | 56 | 35 | 21 | 51 | 60 | |
| M | 56 | 21 | 57 | 78 | 70 | |
| N | 35 | 21 | 36 | 68 | 68 | |
| Pa | 21 | 57 | 36 | 51 | 61 | |
| Pe | 51 | 78 | 68 | 51 | 13 | |
| T | 60 | 70 | 68 | 61 | 13 |
求由上述交通网络数据确定的最小生成树:
clc, clear
a=zeros(6); %邻接矩阵初始化
a(1,[2:6])=[56 35 21 51 60]; %输入邻接矩阵的上三角元素
a(2,[3:6])=[21 57 78 70];
a(3,[4:6])=[36 68 68];
a(4,[5 6])=[51 61]; a(5,6)=13;
a=a'; a=sparse(a); %变换成下三角矩阵,并转化成工具箱所需要的稀疏矩阵
[ST,pred] = graphminspantree(a,'method','Kruskal') %调用工具箱求最小生成树并定义用kruskal算法求解
nodestr={'L','M','N','Pa','Pe','T'}; %输入顶点名称的字符细胞数组
h=view(biograph(ST,nodestr,'ShowArrows','on','ShowWeights','on'))%将节点名称显示在图形上,并显示箭头以及对应的权重
h.EdgeType='segmented'; %边的连接为线段
h.LayoutType='equilibrium'; dolayout(h) %设置图形布局属性,并刷新图形布局graphminspantree不需要指定Direct是0/1,但对于无向图仍然需要将输入得稀疏矩阵转为下三角矩阵。
网络最大流问题:
同样,我们只需调用graphmaxflow函数即可

求最大流:
clc,clear
a=zeros(6);
%标号s=1 v1=2 v3=3 v2=4 v4=5 t=6
a(1,2)=8;a(1,3)=7;
a(2,3)=5;a(2,4)=9;
a(3,5)=9;
%有向图 不是上三角或下三角矩阵
a(4,3)=2;a(4,6)=5;
a(5,4)=6;a(5,6)=10;
%有向图 直接取稀疏矩阵
a=sparse(a);
%1,6表示求源点s和汇点t之间的最大流
[b,c]=graphmaxflow(a,1,6)
%b返回最大流 c返回每条管道对应的流量得:
b =
14
c =
(1,2) 8.0000
(1,3) 6.0000
(2,3) 1.0000
(4,3) 2.0000
(2,4) 7.0000
(3,5) 9.0000
(4,6) 5.0000
(5,6) 9.0000
最大流最小费用问题再加上一定的约束即可,这里不再细说.
旅行商问题
旅行商问题是经典得哈密顿圈图论问题,具体可以自行百度其原理。这里给出lingo求解源码,只需带入初始矩阵即可。
约束条件:

+
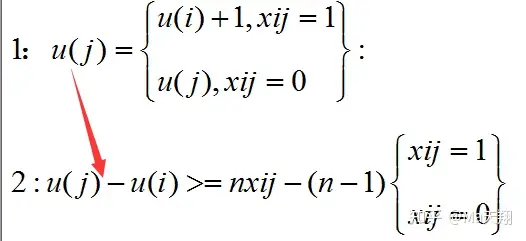
1=2 转换为不等式使程序求解速度更快
model:
sets:city / 1..10/: u;link(city, city):dist,x;
endsets n = @size(city);
data: dist = 0 8 5 9 12 14 12 16 17 228 0 9 15 17 8 11 18 14 225 9 0 7 9 11 7 12 12 179 15 7 0 3 17 10 7 15 1812 17 9 3 0 8 10 6 15 1814 8 11 17 8 0 9 14 8 1612 11 7 10 10 9 0 8 6 1116 18 12 7 6 14 8 0 11 1117 14 12 15 15 8 6 11 0 1022 22 17 18 15 16 11 11 10 0;
enddatamin = @sum(link:dist*x);@FOR(city(K):@sum(city(I)|I#ne#K:x(I,K)=1;@sum(city(J)|J#ne# K: x( K, J))=1;);@for(city(I)|I#gt#1:@for(city(J)|J#gt#1#and#I#ne#J:u(I)-u(J)+n*x(I,J)<=n-1););@for(city(I)|I#gt#1:u(I)<=n-2);@for(link:@bin(x));
end
!只需替换data中 dist的距离矩阵以及初始化条件city的维数即可总结
对于求解最小路径、最大流、最小生成树等问题使用matalab工具箱函数即可。统一的,对于有向图直接取稀疏矩阵,对于无向图需要取其下三角矩阵再求稀疏矩阵。
写了一天,累die....打球去了,希望可以帮助更多的人更好的理解和运用这些算法。如有不当,请指正。
参考书目:
数学建模算法与应用
数学模型算法与应用模型与解答
相关文章:
数学建模-图与网络模型解题方法和代码实现
本文针对以下几个方面问题进行整理: 最短路问题 两个指定顶点之间的最短路径任意顶点之间的最短路径 2.最小生成树问题 求最小生成树 3.网络最大流问题 源点与汇点之间的最大流基于最大流的最小费用求解 4.旅行商问题 基于哈密顿(Hamilton)圈求解旅行商线性…...

宏集新闻 | 虹科传感器事业部正式更名为宏集科技
致一直支持“虹科传感器”的朋友们: 为进一步整合资源,给您带来更全面、更优质的服务,我们非常荣幸地宣布,虹科传感器事业部已正式更名为宏集科技。这一重要的改变代表了虹科持续发展进程中的新里程碑,也体现了我们在传…...

DataFunSummit:2023年数据基础架构峰会-核心PPT资料下载
一、峰会简介 正如From、Join、排序等是SQL的基本算子,存储与计算是也是数据架构中数据生产与消费的基本算子,对于数据架构之下的技术栈层级,我们可将其定义为数据基础架构。 数据存储技术在适应大数据时代的规模需求基础之上,持…...
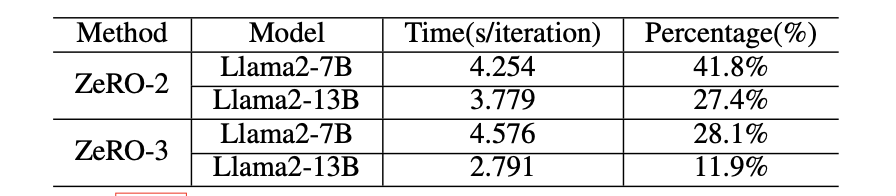
解析大型语言模型的训练、微调和推理的运行时性能
背景 这篇论文是截至目前为数不多的介绍大模型训练配套环境比对的论文,对于想要入门大模型训练同学是个不错的入门资料。比较了不同尺寸模型(比较常用的7、13、70b),在不同型号gpu、训练框架、推理框架数据。结合自己实际工作需要…...
MAX/MSP SDK学习06:内存管理
提供两种内存分配方式:①简单指针,②句柄(二级指针);官方文档建议使用前者。 // 简单指针 char *ptr; ptr sysmem_newptr(2000); post("I have a pointer %lx and it is %ld bytes in size",ptr, sysmem_p…...
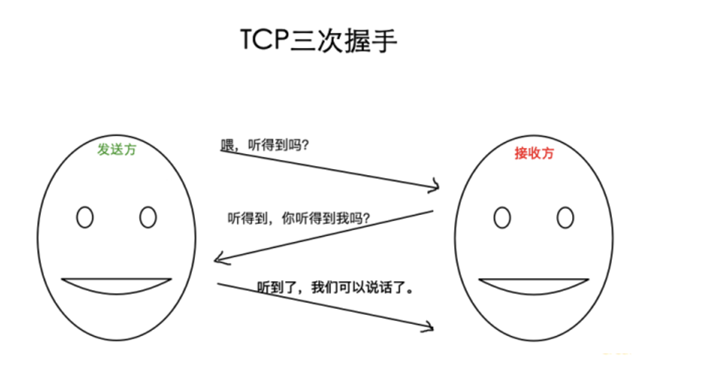
python网络通信之基础知识填坑
文章目录 版权声明网络通信要素IP地址ifconfig和ping命令ifconfig (Interface Configuration)ping 端口和端口号的介绍端口号的分类socket介绍TCPTCP简介TCP的特点 UDPUDP简介UDP特点 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明&#…...

【腾讯云云上实验室-向量数据库】腾讯云开创新时代,发布全新向量数据库Tencent Cloud VectorDB
前言 随着人工智能、数据挖掘等技术的飞速发展,海量数据的存储和分析越来越成为重要的研究方向。在海量数据中找到具有相似性或相关性的数据对于实现精准推荐、搜索等应用至关重要。传统关系型数据库存在一些缺陷,例如存储效率低、查询耗时长等问题&…...
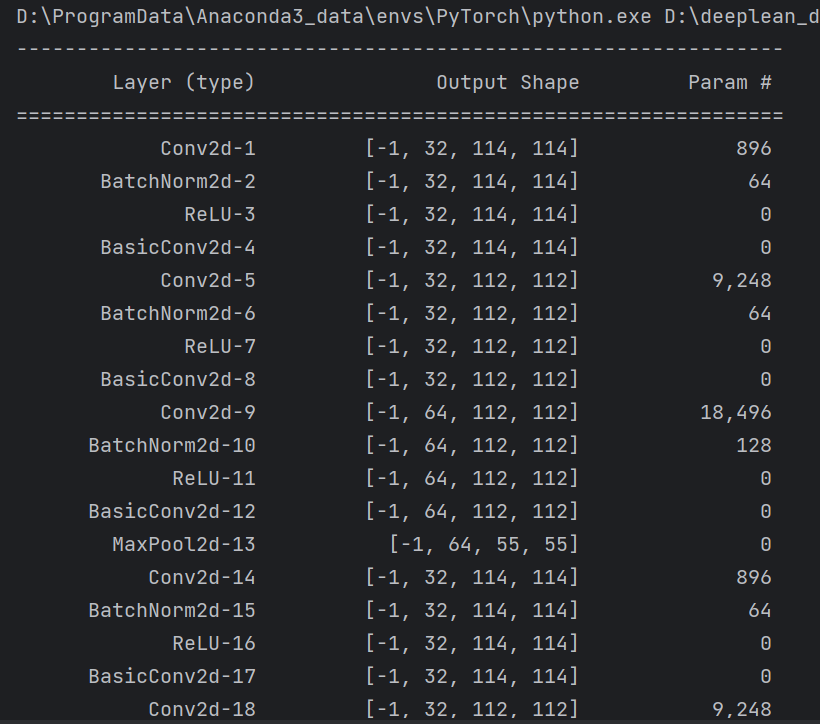
【图像分类】【深度学习】【Pytorch版本】GoogLeNet(InceptionV4)模型算法详解
【图像分类】【深度学习】【Pytorch版本】GoogLeNet(InceptionV4)模型算法详解 文章目录 【图像分类】【深度学习】【Pytorch版本】GoogLeNet(InceptionV4)模型算法详解前言GoogLeNet(InceptionV4)讲解Stem结构Inception-A结构Inception- B结构Inception-C结构Redution-A结构Re…...

opencv dots_image_kernel
1,opencv dots_image_kernel // halcon dots_image kernel估算(d5) cv::Mat getDotKernel(int d 5){// 保证d为正的奇数d | 0x01;cv::Mat kernel cv::Mat::zeros(d 2, d 2, CV_8UC1);int cx kernel.cols / 2;int cy kernel.rows / 2;int cnt255 0, cnt128 …...
使用pytorch利用神经网络原理进行图片的训练(持续学习中....)
1.做这件事的目的 语言只是工具,使用python训练图片数据,最终会得到.pth的训练文件,java有使用这个文件进行图片识别的工具,顺便整合,我觉得Neo4J正确率太低了,草莓都能识别成为苹果,而且速度慢,不能持续识别视频帧 2.什么是神经网络?(其实就是数学的排列组合最终得到统计结果…...

2023年中国合成云母行业现状及市场格局分析[图]
合成云母是一种通过化工原料经高温熔融冷却析晶而制得的单斜晶系矿物,属于典型的层状硅酸盐,许多性能都优于天然云母,如合成云母的耐温高达1200℃以上,而天然白云母在550℃下就会开始分解,金云母则在800℃开始分解。除…...

Vue3+Vite实现工程化,插值表达式和v-text以及v-html
1、插值表达式 插值表达式最基本的数据绑定形式是文本插值,它使用的是"Mustache"语法,即 双大括号{{}} 插值表达式是将数据 渲染 到元素的指定位置的手段之一插值表达式 不绝对依赖标签,其位置相对自由插值表达式中支持javascript的…...

艾泊宇产品战略:灵感于鬼屋,掌握打造卓越用户体验的关键要素
在当今的商业环境中,用户体验已经成为产品成功的关键因素。 无论是线上产品还是实体产品,用户体验都是决定用户是否愿意使用和推荐该产品的关键因素。 那么,艾泊宇产品战略理论告诉大家,如何做好用户体验? 我们可以…...
深度学习环境配置(Anaconda+pytorch+pycharm+cuda)
NVIDIA驱动安装 首先查看电脑的显卡版本,步骤为:此电脑右击-->管理-->设备管理器-->显示适配器。就可以看到电脑显卡的版本了。 然后按照电脑信息,到地址 去安装相应的驱动,Notebooks是笔记本的意思,然后下…...
不是说人工智能是风口吗,那为什么工作还那么难找?
最近确实有很多媒体、机构渲染人工智能可以拿高薪,这在行业内也是事实,但前提是你有足够的竞争力,真的懂人工智能。 首先,人工智能岗位技能要求高,人工智能是一个涵盖了多个学科领域的综合性学科,包括数学、…...
 发生了什么)
new Vue() 发生了什么
前言: 在Vue.js中,当你创建一个新的Vue实例时,通过 new Vue() 发生了一系列重要的操作,包括Vue实例的初始化、数据绑定、模板编译等。这个过程是Vue应用的核心,本文将深入探讨new Vue()发生了什么以及其原理,提供示例…...

【算法】二叉树的存储与遍历模板
二叉树的存储与遍历 const int N 1e6 10;// 二叉树的存储,l数组为左节点,r数组为右结点 int l[N], r[N]; // 存储节点的数据 char w[N]; // 节点的下标指针 int idx 0;// 先序创建 int pre_create(int n) {cin >> w[n];if (w[n] #) return -1;l[n] pre_create(idx)…...
【Go学习之 go mod】gomod小白入门,在github上发布自己的项目(项目初始化、项目发布、项目版本升级等)
参考 Go语言基础之包 | 李文周的博客Go mod的使用、发布、升级 | weiGo Module如何发布v2及以上版本1.2.7. go mod命令 — 新溪-gordon V1.7.9 文档golang go 包管理工具 go mod的详细介绍-腾讯云开发者社区-腾讯云Go Mod 常见错误的原因 | walker的博客 项目案例 oceanweav…...
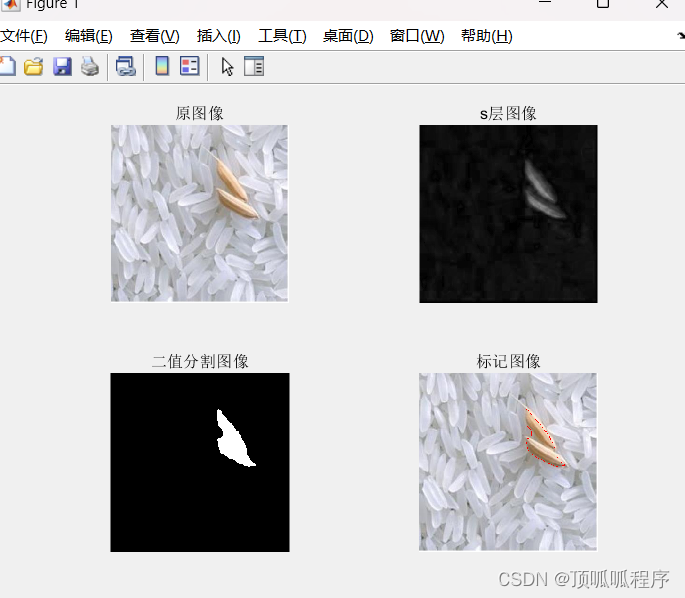
79基于matlab的大米粒中杂质识别
基于matlab的大米粒中杂质识别,数据可更换自己的,程序已调通,可直接运行。 79matlab图像处理杂质识别 (xiaohongshu.com)...

Vue 项目实战——如何在页面中展示 PDF 文件以及 PDFObject 插件实战
文章目录 📋前言🎯使用 HTML 标签🧩 embed 标签🧩 object标签🧩 iframe标签🧩完整代码 🎯使用 PDFObject 插件🧩为什么使用 PDFObject 插件(AI翻译)…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
