赋范线性空间3
赋范线性空间三
文章目录
- 赋范线性空间三
- 三、内积空间
- 3.1 内积空间的定义和性质
- 【定义】内积
- 【定理】内积的性质——Schwarz不等式
- 【定义】有内积导出的范数
- 【定理】内积、由内积导出的范数 的性质
- 3.2 正交与正交系
- 【定义】正交、正交补
- 【定理】勾股定理在内积空间中的推广
- 【定义】正交系、标准正交系
- 【定理】Bessel 不等式(标准正交系推出的性质)
- 【定义】完全系
- 【定理】完全系的等价描述
- 【定理】Gram-Schmidt 正交化
- 【定理】可分的Hilbert空间必存在完全的标准正交系
- 【定义】内积空间的同构
- 【定理】任何可分[^3]的无穷维Hilbert空间都与 l² 等距同构
三、内积空间
赋范线性空间是定义了向量长度的线性空间,但有时还会对向量的夹角感兴趣,因此引入内积。
3.1 内积空间的定义和性质
内积同样可以自行定义,但应满足以下基本条件:
【定义】内积
设 X X X 是数域 F F F (实数域or复数域)上的线性空间,若映射 < ⋅ , ⋅ > : X × X → F <\cdot,\cdot>:X\times X\to F <⋅,⋅>:X×X→F 满足 ∀ x , y , z ∈ X , α , β ∈ F \forall x,y,z\in X,\alpha,\beta\in F ∀x,y,z∈X,α,β∈F
- 正定性: < x , x > ≥ 0 <x,x>\geq0 <x,x>≥0,取等号当且仅当 x = 0 x=0 x=0
- 共轭对称性: < x , y > = < y , x > ‾ <x,y>=\overline{<y,x>} <x,y>=<y,x>(这里的共轭指复数的共轭)
- 第一变元线性性: < α x + β y , z > = α < x , z > + β < y , z > <\alpha x+\beta y,z>=\alpha<x,z>+\beta<y,z> <αx+βy,z>=α<x,z>+β<y,z>,其中 α , β ∈ F \alpha,\beta\in F α,β∈F
【定理】内积的性质——Schwarz不等式
∣ < x , y > ∣ ≤ < x , x > < y , y > |<x,y>|\leq\sqrt{<x,x>}\sqrt{<y,y>} ∣<x,y>∣≤<x,x><y,y>
【定义】有内积导出的范数
设 X X X 为内积空间, ∀ x ∈ X \forall x\in X ∀x∈X,记
- ∥ x ∥ = < x , x > \|x\|=\sqrt{<x,x>} ∥x∥=<x,x>
称 ∥ ⋅ ∥ \|\cdot\| ∥⋅∥ 为由 X X X 上的内积导出来的范数
【定理】内积、由内积导出的范数 的性质
设 X X X 为内积空间, x , y ∈ X x,y\in X x,y∈X,则对于内积和由内积导出的范数,有
平行四边形公式 ∥ x + y ∥ 2 + ∥ x − y ∥ 2 = 2 ( ∥ x ∥ 2 + ∥ y ∥ 2 ) \|x+y\|^2+\|x-y\|^2=2(\|x\|^2+\|y\|^2) ∥x+y∥2+∥x−y∥2=2(∥x∥2+∥y∥2)
极化恒等式
当 X X X 为实内积空间时
< x , y > = 1 4 ( ∥ x + y ∥ 2 − ∥ x − y ∥ 2 ) <x,y>=\frac14(\|x+y\|^2-\|x-y\|^2) <x,y>=41(∥x+y∥2−∥x−y∥2)
当 X X X 为复内积空间时
< x , y > = 1 4 ( ∥ x + y ∥ 2 − ∥ x − y ∥ 2 + i ∥ x + i y ∥ 2 − i ∥ x − i y ∥ 2 ) <x,y>=\frac14(\|x+y\|^2-\|x-y\|^2+i\|x+iy\|^2-i\|x-iy\|^2) <x,y>=41(∥x+y∥2−∥x−y∥2+i∥x+iy∥2−i∥x−iy∥2)
3.2 正交与正交系
有了内积的定义,空间中就有了夹角的概念,相应的也就有了正交这样的几何概念
【定义】正交、正交补
设 X X X 为内积空间, x , y ∈ X x,y\in X x,y∈X,若 < x , y > = 0 <x,y>=0 <x,y>=0,则称 x x x 与 y y y 是正交的,记为 x ⊥ y x\perp y x⊥y
设 X , Y ⊂ X X,Y\subset X X,Y⊂X,若 ∀ x ∈ A , y ∈ B \forall x\in A,y\in B ∀x∈A,y∈B,有 x ⊥ y x\perp y x⊥y,就称 A A A 与 B B B 正交,记为 A ⊥ B A\perp B A⊥B,特别的 { x } ⊥ B \{x\}\perp B {x}⊥B 记为 x ⊥ B x\perp B x⊥B
记 A ⊥ = { x ∣ x ⊥ A } A^{\perp}=\{x|x\perp A\} A⊥={x∣x⊥A},称 A ⊥ A^\perp A⊥ 为 A A A 的正交补
【定理】勾股定理在内积空间中的推广
设 X X X 为内积空间, x , y ∈ X x,y\in X x,y∈X, x ⊥ y x\perp y x⊥y,则有
∥ x + y ∥ 2 = ∥ x ∥ 2 + ∥ y ∥ 2 \|x+y\|^2=\|x\|^2+\|y\|^2 ∥x+y∥2=∥x∥2+∥y∥2
对任意有限个相互正交的元素,有
∥ ∑ i = 1 n x i ∥ 2 = ∑ i = 1 n ∥ x i ∥ 2 \left\|\sum_{i=1}^n x_i\right\|^2=\sum_{i=1}^n \left\|x_i\right\|^2 i=1∑nxi 2=i=1∑n∥xi∥2
【定义】正交系、标准正交系
设 X 为内积空间, E = { e i ∣ i ∈ I } E=\{e_i|i\in I\} E={ei∣i∈I} 为一簇非零元素,其中 I I I 为某一非空集合,
- 若其中任意两元素均正交,则称 E E E 为 X X X 中的正交系
- 若还满足 ∀ e i ∈ E \forall e_i\in E ∀ei∈E, ∥ e i ∥ = 1 \|e_i\|=1 ∥ei∥=1,则称 E E E 为标准正交系
【定理】Bessel 不等式(标准正交系推出的性质)
设 X 为内积空间, E = { e i ∣ i ∈ Z + } E=\{e_i|i\in\mathbb{Z}_+ \} E={ei∣i∈Z+} 为标准正交系,则 ∀ x ∈ X \forall x\in X ∀x∈X,有
∥ x ∥ 2 ≥ ∑ i = 1 ∞ ∣ < x , r i > ∣ 2 \|x\|^2\geq\sum_{i=1}^\infty|<x,r_i>|^2 ∥x∥2≥i=1∑∞∣<x,ri>∣2
【定义】完全系
设 X 为内积空间, E = { e i ∣ i ∈ Z + } E=\{e_i|i\in\mathbb{Z}_+ \} E={ei∣i∈Z+} 为标准正交系,若只有零元与一切 e i ∈ E e_i\in E ei∈E 都正交,则称 E E E 是个完全系
【定理】完全系的等价描述
设 X X X 是 Hilbert 空间1, E = { e i ∣ i ∈ Z + } E=\{e_i|i\in\mathbb{Z}_+ \} E={ei∣i∈Z+} 为标准正交系,则下列说法等价:
- E E E 是完全系
- ∀ x ∈ X \forall x\in X ∀x∈X, x = ∑ i = 1 ∞ < x , e i > e i x=\sum_{i=1}^{\infty}<x,e_i>e_i x=∑i=1∞<x,ei>ei
- Parseval 等式成立,即 ∀ x ∈ X \forall x\in X ∀x∈X,有 ∥ x ∥ 2 = ∑ i = 1 ∞ ∣ < x , e i > ∣ 2 \|x\|^2=\sum_{i=1}^\infty|<x,e_i>|^2 ∥x∥2=∑i=1∞∣<x,ei>∣2
【定理】Gram-Schmidt 正交化
设 B = { x n ∣ n ∈ Z + } B=\{x_n|n\in \mathbb{Z}_+\} B={xn∣n∈Z+} 是内积空间 X X X 的可数子集,则存在标准正交系 E = { e n ∣ n ∈ Z + } E=\{e_n|n\in\mathbb{Z}_+ \} E={en∣n∈Z+} 使得 s p a n B = s p a n E spanB=spanE spanB=spanE2
【定理】可分的Hilbert空间必存在完全的标准正交系
设 X X X 是可分3的Hilbert空间,则 X X X 中必存在完全的标准正交系
【定义】内积空间的同构
设 X , Y X,Y X,Y 是同一数域上的内积空间, T T T 是 X X X 到 Y Y Y 的线性同构映射,
- 若 T T T 还保持内积,即 ∀ x , y ∈ X \forall x,y\in X ∀x,y∈X, < T x , T y > = < x , y > <Tx,Ty>=<x,y> <Tx,Ty>=<x,y>
则称 T T T 为内积空间上的同构映射,称 X , Y X,Y X,Y 作为内积空间是同构的
【定理】任何可分3的无穷维Hilbert空间都与 l² 等距同构
【Hilbert空间】备的内积空间称为Hilbert空间 ↩︎
【span】线性空间内所有元素对于加法、数乘封闭,这些元素所有可能的线性组合记作 S p a n Span Span ↩︎
【可分】设 A , B A,B A,B 为度量空间 X X X 中的子集,若 B ⊂ A ‾ B\subset\overline A B⊂A ,就称 A A A 在 B B B 中稠密,若一个可数集 A A A 在 X X X 中稠密,则称 X X X 是可分的。 ↩︎ ↩︎
相关文章:

赋范线性空间3
赋范线性空间三 文章目录 赋范线性空间三三、内积空间3.1 内积空间的定义和性质【定义】内积【定理】内积的性质——Schwarz不等式【定义】有内积导出的范数【定理】内积、由内积导出的范数 的性质 3.2 正交与正交系【定义】正交、正交补【定理】勾股定理在内积空间中的推广【定…...
)
XSLVGL2.0 User Manual 缩略图生成器(v2.0)
XSLVGL2.0 开发手册 XSLVGL2.0 User Manual 缩略图生成器 1、概述2、特性3、APIs3.1、xs_system_init_thumbnail3.2、xs_system_exit_thumbnail3.3、xs_system_get_thumbnail3.4、xs_system_thumbnail_on_cache_to_storage_defalut4、使用方法5、自定义缩略图生成方法1、概述 …...
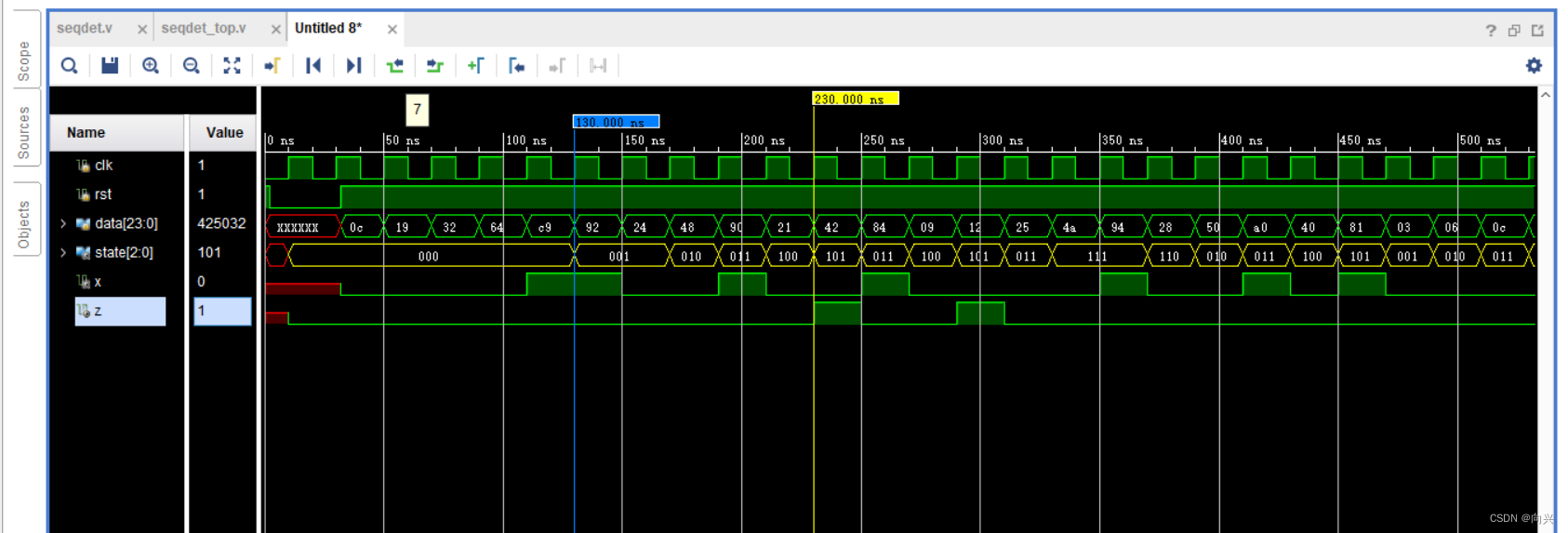
练习八-利用有限状态机进行时序逻辑的设计
利用有限状态机进行时序逻辑的设计 1,任务目的:2,RTL代码,及原理框图3,测试代码,输出波形 1,任务目的: (1)掌握利用有限状态机实现一般时序逻辑分析的方法&am…...

WebAssembly照亮了 Web端软件的未来
WebAssembly的发展历程相对较短,但影响深远。WebAssembly 于 2015 年首次发布,先驱技术是来自Mozilla的asm.js和Google Native Client,最初的实现是基于asm.js的功能集。自2017年3月由WebAssembly创造的MVP的预览版发布以来,WebAs…...
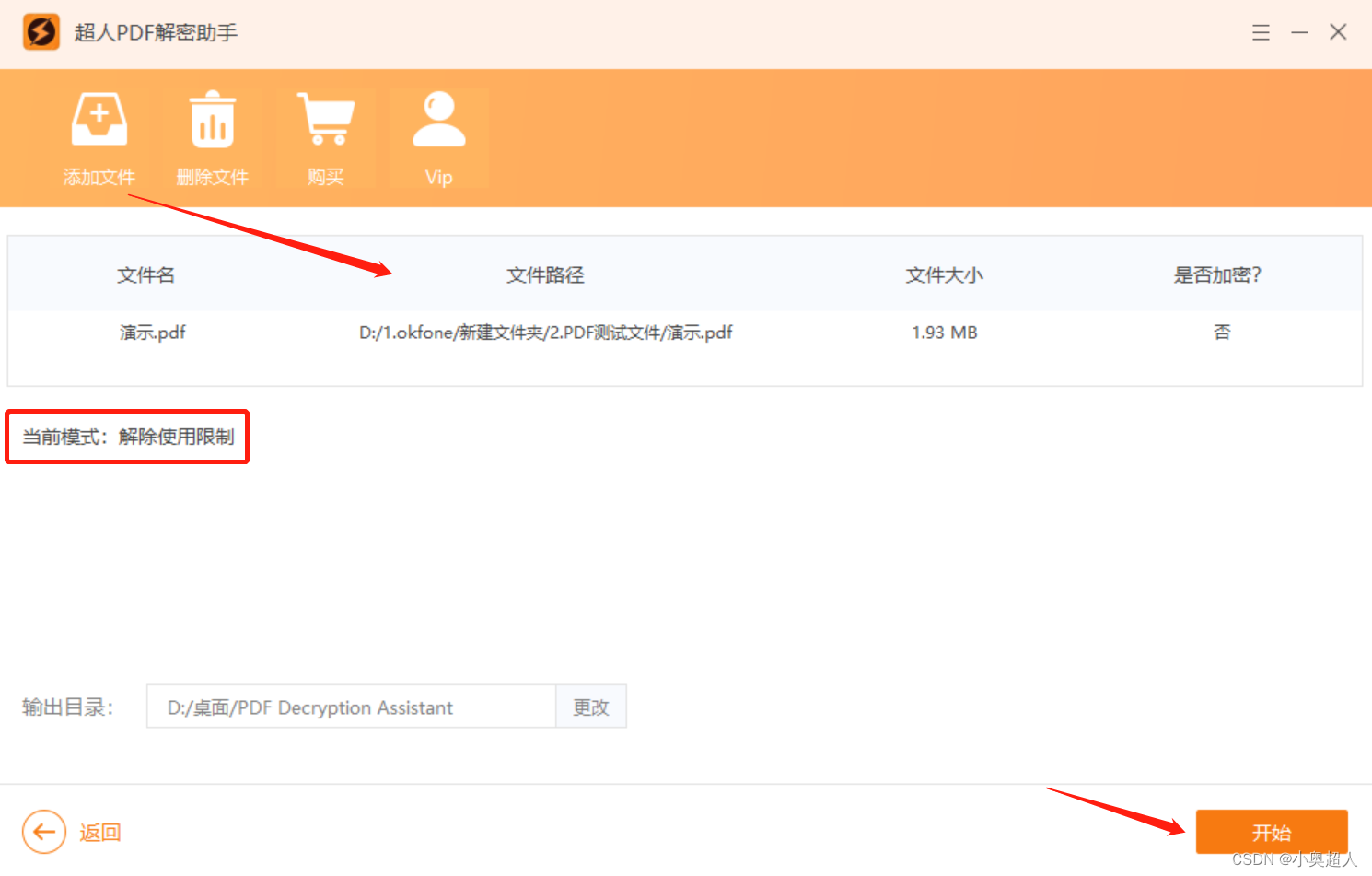
PDF文件无密码,如何解密?
PDF文件有两种密码,一个打开密码、一个限制编辑密码,因为PDF文件设置了密码,那么打开、编辑PDF文件就会受到限制。想要解密,我们需要输入正确的密码,但是有时候我们可能会出现忘记密码的情况,或者网上下载P…...

搜维尔科技:Movella Xsens MVN LINK 实际应用,一镜到底!
搜维尔科技:Movella Xsens MVN LINK 实际应用,一镜到底!...

wsl安装ubuntu的问题点、处理及连接
WSL安装Ubuntu的参考链接 (41条消息) wsl报错:WslRegisterDistribution failed with error: 0x800701bc_yzpyzp的博客-CSDN博客_0x800701bc wsl (41条消息) 使用Ubuntu安装软件出现Unable to locate package错误解决办法_大灰狼学编程的博客-CSDN博客 手把手教你…...

Flutter在web项目中使用iframe
需要把原来的app项目移植到web上面,在app中使用的是flutter_inappwebview这个库,推荐使用这个库,因为修复了一部分webview_flutter中存在的问题 在web项目中flutter_inappwebview这个库不支持,所以需要自己封装一个web项目中的we…...

阿里云高校计划学生和教师完成认证领取优惠权益
阿里云高校计划学生和教师均可参与,完成学生认证和教师验证后学生可以免费领取300元无门槛代金券和3折优惠折扣,适用于云服务器等全量公共云产品,订单原价金额封顶5000元/年,阿里云百科aliyunbaike.com分享阿里云高校计划入口及学…...

劲松HPV防治诊疗中心提醒:做完HPV检查后,需留意这些事项!
在接受HPV检查后,有一些注意事项需要您注意。首先,要遵循医生的建议,并按照医生的指示进行后续治疗和随访。 其次,检查后可能会有些不适感,这是正常的现象,不必过于担心。但是,如果不适感持续加…...

InfoNCE Loss公式及源码理解
InfoNCE Loss公式及源码理解–从交叉熵损失谈起 当谈论到信息论中的损失函数时,InfoNCE(Noise Contrastive Estimation)和交叉熵损失都是两个关键的概念。它们不仅在衡量概率分布之间的差异方面发挥着重要作用,而且在深度学习的自…...

经典双指针算法试题(二)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、有效三角形的个数1、题目讲解2、讲解算法原理3、代码实现 二、查找总价格为目标值的两个商…...

MySQL -- DQL
1、select查询列和列名: --查询所有员工信息(*通配符,默认查询所有的列) select * from emp;--查询员工的姓名 select ename from emp;--查询员工的薪资 select sal from emp;--查询员工的姓名和薪资 select ename , sal from emp; select ename sal fr…...

高防CDN:保障网络安全的未来之路
在当前数字化飞速发展的时代,网络安全问题日益成为企业和个人关注的焦点。高防CDN(Content Delivery Network,内容分发网络)作为一种专注于防御网络攻击的解决方案,尽管在技术上表现卓越,但其普及却面临一系…...
使用wxPython和PyMuPDF合并PDF文档并自动复制到剪贴板
导语:处理大量的PDF文档可能会变得复杂和耗时。但是,使用Python编程和一些强大的库,如wxPython和PyMuPDF,可以使这个任务变得简单而高效。本文将详细解释一个示例代码,展示如何使用这些库来创建一个可以选择文件夹中的…...

Redis篇---第十四篇
系列文章目录 文章目录 系列文章目录前言一、为什么Redis的操作是原子性的,怎么保证原子性的?二、了解Redis的事务吗?四、Redis 的数据类型及使用场景前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男…...

python之文件操作
文件的读取、修改、写入 知识点:不可以使用for循环生成变量,替代方式:将每次循环生成的数据添加到列表中,再对列表进行操作 例子:根据输入的环境名称操作hosts文件,注释掉其他环境 #env1 127.0.0.1 127.0.…...

android实时投屏软件QtScrcpy
QtScrcpy 可以通过 USB / 网络连接Android设备,并进行显示和控制。无需root权限。 同时支持 GNU/Linux ,Windows 和 MacOS 三大主流桌面平台。 QtScrcpy: Android实时投屏软件,此应用程序提供USB(或通过TCP/IP)连接的Android设备的显示和控制…...
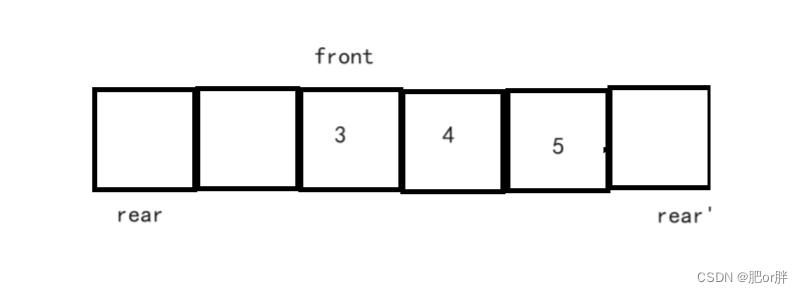
LeetCode - 622. 设计循环队列(C语言,顺序存储结构,配图)
目录 编辑定义结构体: 1. MyCircularQueue(k): 构造器,设置队列长度为 k 2. Front: 从队首获取元素。如果队列为空,返回 -1 3. Rear: 获取队尾元素。如果队列为空,返回 -1 4. enQueue(value): 向循环队列插入一个元素。…...

在 Qt 框架中,有许多内置的信号可用于不同的类和对象\triggered
在 Qt 框架中,有许多内置的信号可用于不同的类和对象 以下是一些常见的内置信号的示例: clicked():按钮(QPushButton、QToolButton 等)被点击时触发的信号。 pressed() 和 released():按钮被按下和释放时…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
