取数游戏2(动态规划java)
取数游戏2
题目描述
给定两个长度为n的整数列A和B,每次你可以从A数列的左端或右端取走一个数。假设第i次取走的数为ax,则第i次取走的数的价值vi=bi⋅ax,现在希望你求出∑vi的最大值。
输入格式
第一行一个数T ,表示有T 组数据。对于每组数据,第一行一个整数 n ,接下来两行分别给出 A 数列与B 数列。
输出格式
每一组数据输出一行,最大的∑vi。
样例输入输出
样例输入
2
2
1 1000
2 1
5
1 3 5 2 4
1 2 3 4 5
样例输出
2001
52
数据范围
对于100的数据,保证 T≤10,1≤n≤1000,1≤ai,bi≤1000。
算法思路
首先题目中说的是每次取A数列的左端或右端,而B数列取的是第i个元素,暴力解的思路肯定就是通过回溯算法,把所有的情况尝试出来,但是这种思路肯定是会超时的,所以采用优化的算法动态规划。
首先定义dp数组的意义,因为最后要求的是A数列和B数列得出的∑vi最大值,所以可以定义为dp[0][n-1]为A数列[0 ~ n-1]得出的∑vi最大值,而dp[i][j]表示的是A数列[i ~ j]计算出来的∑vi最大值。
按照这个思路继续,继续推断递推公式,因为题干中说的是每次从A数列左端或右端取走一个数,并且乘上B数列的第i个元素,我们可以反向操作,初始的时候A数列没有元素,每次在左端或右端添加一个数,并且乘上B数列的第n-i个元素,通过这种逆向思路变可以推断出递推公式,既然每次是在左端或右端添加数,对于dp[i][j]的值来说,可能是由于dp[i+1][j]添加左端的数并且乘上B数列对应的元素得到的,也可能是dp[i][j-1]乘上B数列对应的元素得到的,取两者的最大值,那么就可以得出递推公式是dp[i][j]=max(dp[i+1][j]+B[n-j+i-1]*A[i],dp[i][j-1]+B[n-j+i-1]*A[j]),其中B[n-j+i-1]是左端或者右端添加数对应的B数列元素。
那么最后就是开始遍历dp数组来算出每个值了,其中dp数组的初始化有一个规律,就是最开始取的A数列的元素一定是乘上B数列中的最后的元素,因为dp[i]j的时候代表的意义一定是只有一个数的时候,所以在初始化dp数组的时候,让dp对角线元素等于A数列对应的元素乘上B数列最后一个元素作为初始值。
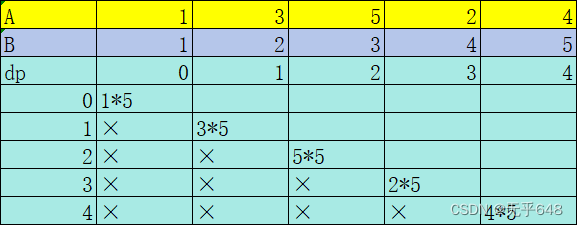
如上图,按照题干的测试案例给出的每个数组的值,其中dp数组是按照下面的元素和左面的元素来推断出来的,最后dp[0][4]便是答案。
代码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int T = scanner.nextInt();while (T>0){T-=1;//定义输入数据的初始化int n = scanner.nextInt();int []A = new int[n];int []B = new int[n];int [][]dp=new int[n][n];for(int i=0;i<n;++i){A[i]= scanner.nextInt();}for(int i=0;i<n;++i){B[i]= scanner.nextInt();}//让对角线上的元素等于B数组最后一个元素和A数组的第i个元素,动态规划的数组初始化for(int i=0;i<n;++i){dp[i][i]=A[i]*B[n-1];}for(int i=n-1;i>=0;i--){for(int j=i+1;j<n;++j){//递推公式dp[i][j]=Math.max(dp[i+1][j]+B[n-j+i-1]*A[i],dp[i][j-1]+B[n-j+i-1]*A[j]);}}System.out.println(dp[0][n-1]);}}
}
相关文章:

取数游戏2(动态规划java)
取数游戏2 题目描述 给定两个长度为n的整数列A和B,每次你可以从A数列的左端或右端取走一个数。假设第i次取走的数为ax,则第i次取走的数的价值vibi⋅ax,现在希望你求出∑vi的最大值。 输入格式 第一行一个数T ,表示有T 组数据。…...

Spring Boot中配置文件生效位置
1. 配置文件位置 首先小伙伴们要明白,Spring Boot 默认加载的配置文件是 application.properties 或者 application.yaml,properties优先级高于yaml。默认的加载位置一共有五个,五个位置可以分为两类: 从 classpath 下加载&…...
AIGC创作系统ChatGPT网站系统源码,支持最新GPT-4-Turbo模型
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...
【JavaEE】操作系统与进程
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《JavaEE》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&…...
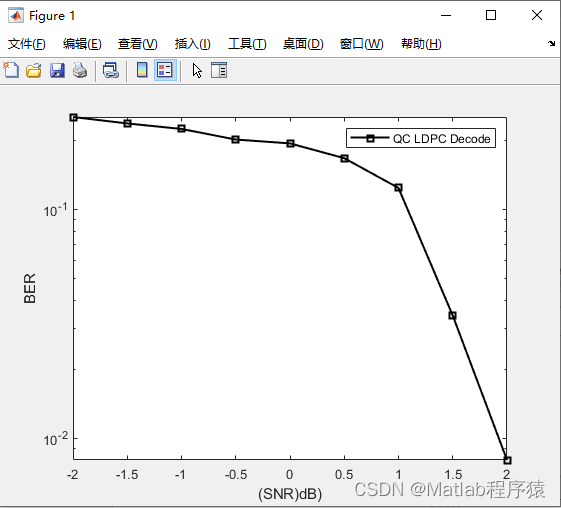
【MATLAB源码-第86期】基于matlab的QC-LDPC码性能仿真,输出误码率曲线。
操作环境: MATLAB 2022a 1、算法描述 QC-LDPC(准循环低密度奇偶校验)编码是一种高效的错误校正编码方式,广泛应用于通信系统和数据存储中以提高数据的可靠性。它是低密度奇偶校验(LDPC)编码的一种特殊形…...
)
【0236】聊一聊PG内核中的命令标签(Command Tags、CommandTag、tag_behavior)
1. 什么是命令标签(Command Tags) 当客户端向PG服务下发一个请求时,postgres进程在读取到用户的请求缓冲区之后,需要对从中解析出用户的具体请求,比如:CREATE TABLE、CREATE DATABASE、DROP TABLE、SELECT等具体操作,这里除了会用到后面即将讲的词法分析解析器flex之外…...
Python武器库开发-flask篇之error404(二十七)
flask篇之error404(二十七) 首先,我们先进入模板的界面创建一个404的html页面 cd templates vim 404.html404.html的内容如下: <h1>error!!!</h1>在 Flask 应用程序中,当用户访问一个不存在的页面的时候,会出现 4…...
录屏软件自动开启录视频,是如何实现的?
工作要留痕,作为职场人的一项必备技能,因此许多人在做一些重要操作的时候,就会提前开启录屏软件,把操作的每一个步骤进行录制,以避免在出现问题的时候进行检查。当每天都需要在固定的时间点重复某项工作的时候…...

模拟shell小程序
接下来利用我们当前的知识,撰写一个简单的shell外壳程序。 1.shell原理 shell的原理是实际上就是运行了一个父进程,然后创建出子进程,最后使用进程替换调用,替换成其他程序。 2.shell实现 2.1.死循环 首先一个shell一旦运行起…...

webpack配置全局scss
webpack配置全局scss 效果:a.vue使用index.scss中定义的$mainWidth就无需 import "xxxxxxx/index.scss"文件 src/assets/styles/index.scss $mainWidth: 1280px; $red: red src/views/a.vue .aaa {color: $red; } vue.config.js module.exports {…...

想面试前端工程师,必须掌握哪些知识和技能?【云驻共创】
在当今的数字化时代,前端工程师扮演着至关重要的角色。他们负责设计和开发用户界面,使得用户能够与应用程序或网站进行互动。为了找到最出色的前端工程师,你需要了解哪些技能和知识是必备的,同时也要掌握一些面试技巧和常见的面试…...

京东数据分析(京东数据采集):2023年10月京东平板电视行业品牌销售排行榜
鲸参谋监测的京东平台10月份平板电视市场销售数据已出炉! 根据鲸参谋电商数据分析平台的相关数据显示,10月份,京东平台上平板电视的销量将近77万,环比增长约23%,同比则下降约30%;销售额为21亿,环…...
 或者 运算符来执行多条命令)
在 Linux 中,可以使用分号 (;) 或者 运算符来执行多条命令
在 Linux 中,你可以使用分号 (;) 或者 && 运算符来执行多条命令。 使用分号 (;) 分隔多条命令: command1 ; command2 这样会依次执行 command1 和 command2,不管前面的命令是否成功。 使用 && 运算符分隔多条命令࿱…...

一些必备的 Redis 命令 | Navicat
Redis 是一种快速的内存数据结构存储系统,因其处理键值对的能力而备受推崇。在本文,我们将探索一些不可或缺的 Redis 命令(不包括之前介绍过的涉及键的命令),解锁这个强大工具的真正潜力。同时,我们也将了解…...

神经网络常用激活函数详解
🎀个人主页: https://zhangxiaoshu.blog.csdn.net 📢欢迎大家:关注🔍点赞👍评论📝收藏⭐️,如有错误敬请指正! 💕未来很长,值得我们全力奔赴更美好的生活&…...
UVA11584划分成回文串 Partitioning by Palindromes
划分成回文串 Partitioning by Palindromes 题面翻译 回文子串(palind) 问题描述: 当一个字符串正序和反序是完全相同时,我们称之为“回文串”。例如“racecar”就是一个回文串,而“fastcar”就不是。现在给一个字符串s,把它分…...

第十一章 将对象映射到 XML - 控制流属性的映射形式
文章目录 第十一章 将对象映射到 XML - 控制流属性的映射形式控制流属性的映射形式控制预计属性的可用性禁用映射%XML.Adapter 中的方法 第十一章 将对象映射到 XML - 控制流属性的映射形式 控制流属性的映射形式 对于流属性,XMLPROJECTION 的选项如下:…...

torchvision中的标准ResNet50网络结构
注:仅用以记录学习 打印出来的网络结构如下: from torchvision import models model models.resnet50(pretrainedFalse) print("model: ", model) 结构: ResNet((conv1): Conv2d(3, 64, kernel_size(7, 7), stride(2, 2), padd…...
)
Java 多线程之 synchronized (互拆锁/排他锁/非观锁)
文章目录 一、概述二、使用方法三、测试示例 一、概述 在Java中,synchronized 关键字用于实现线程之间的同步。提供了一种简单而强大的机制来控制多个线程之间的并发访问,确保共享资源的安全性和一致性。它解决了多线程环境中的竞态条件、数据竞争和内存…...

开源vs闭源大模型如何塑造技术的未来?开源模型的优劣势未来发展方向
开源vs闭源大模型如何塑造技术的未来?开源模型的优劣势&未来发展方向 写在最前面一、开源与闭源:定义与历史背景开源和闭源的定义开源大模型:社区驱动的创新 二、开源和闭源的优劣势比较开源大模型(瓶颈)数据&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
