什么是“奥卡姆剃刀”,如何用“奥卡姆剃刀”解决复杂问题?复杂问题简单化
什么是“奥卡姆剃刀”,如何用“奥卡姆剃刀”解决复杂问题?复杂问题简单化
- 问题
- 什么是“奥卡姆剃刀”?
- 如何使用“奥卡姆剃刀”解决问题
- 复杂问题简单化
- “汉隆剃刀”
- 小结
问题
假设你在夜空中看到一颗闪闪发光的「不明飞行物」,你认为这会是什么呢?
A:地心人的飞行器。
B:外星人的飞行器。
C:人类飞机的灯光。
回答类似这种问题,往往越简单的解释,接近真相的可能性越大。
什么是“奥卡姆剃刀”?
在公元 14 世纪左右,有一个来自奥卡姆的威廉,对当时关于「本质」之类的争吵感到厌倦,于是提出了「奥卡姆剃刀」定律。
「奥卡姆剃刀」定律的核心思想可以简单概括为 8 个字:「如无必要,勿增实体」。
也就是说,砍掉那些无用的细枝末节,把复杂的问题简单化,所以,我们也称之为「简约法则」。

奥卡姆的这把「剃刀」出鞘之后,产生了非常广泛、丰富而且深刻的影响。
随着经济社会的发展,有很多问题正在变得越来越复杂,数据和文件变得越来越多,制度和规则变得越来越繁琐,奥卡姆这把闪闪发光的剃刀,正在向更多的领域发起挑战。
如何使用“奥卡姆剃刀”解决问题
在工作、生活和学习的过程中,我们可以运用「奥卡姆剃刀」定律,让事情变得更加简单高效。
比如,在生活中,养成早睡早起、经常运动等习惯,就能自己拥有一个健康的身体。
怎么才能养成良好的运动习惯呢?按照《微习惯》的方法,你不妨从最简单的习惯开始,比如:每天做一个俯卧撑。
运用「奥卡姆剃刀」定律,最简单的方法,往往就是最有效的方法。一件事情,如果用较少的时间和精力就能做好,那为什么还要浪费更多的时间和精力呢?
在遇到问题,需要做决策的时候,不妨运用「奥卡姆剃刀」,避免寻找过于复杂的解决方案,而关注简单可行的方法。 如果用复杂的方法和简单的方法都能解决问题,那么就选择简单的那种方法。
我们把「奥卡姆剃刀」应用到目标管理中,养成了「以终为始」的习惯,找到自己的终极目标,然后对它进行分解,每天关注最重要的一件事,并进行复盘总结,让目标和行动产生关联,做到知行合一。
为了聚焦目标,我们按照「断舍离」的理念,定期查看「数据赋能系统」中记录的时间数据,并问一问自己:如果不做这件事,会有什么后果?
通过认真审视每件事对长期目标的贡献,从中找到一些其实可以不做的事,并从后续的日程计划中排除掉,就能节省出来很多时间,用来去做其他更加重要的事情。
每个人的时间和精力都是有限的,如果目标过于分散的话,就容易导致顾此失彼,分不清「重要的事」和「紧急的事」,结果成为低效的忙碌者,目标也就难以实现。
爱因斯坦说过:
Everything should be made as simple as possible, but not simpler.
这句话有 2 种不同的翻译,
-
第 1 种翻译是:凡事应该尽可能简单,但不能过于简单。
-
第 2 种翻译是:凡事应该尽可能简单,而不是相对简单。
我个人比较认同上面第 1 种翻译,因为我相信「物极必反」,这是世界普遍运行的规律,当一件事物过度简化之后,可能会导致不当的后果。
在一些数据分析报告中,如果使用了太多的垃圾图表,可能是因为过度简化,也可能是因为「偷懒」行为,使用软件的默认设置,让读者无法认识到问题的本质。
复杂问题简单化
比如,在《图表会说话》这本书中,有一个图表,呈现了美国在 100 年内每年人均可获得肉量的演变过程:

如果剔除不相关的、多余的、没有价值的内容(灰色背景、边框、图例、标记、微笑的牛的图片……),使数据的本质显现出来,直观地看到牛肉和鸡肉的价格变化较大,这样图表可以变得更有效、更优雅,这是应用了「奥卡姆剃刀」定律,让图表尽可能简单,但没有过度简单。

把简单的事情复杂化很容易,但是反过来,把复杂的事情简单化并不容易,特别是需要做到理性思考的时候,更加不容易。
“汉隆剃刀”
在现实生活中,绝大多数的问题,其实都是因为无知导致的,并不是有人故意和你唱反调,这就是「汉隆剃刀」原则,算是「奥卡姆剃刀」的一种特殊情况。
有人甚至还把「汉隆剃刀」原则做了进一步的推广:
能解释为愚蠢的,就不要解释为恶意。
能解释为无知的,就不要解释为愚蠢。
能解释为可原谅的错误的,就不要解释为无知。
能用未知的其他原因解释的,就不要解释为错误。
不要恶意揣测别人,其实发生在我们身上的事情,99.99% 的问题都可以用逻辑分析得清清楚楚,一旦你习惯了用理性的、逻辑的分析方法,就不容易被他人欺骗,更不会被自己欺骗。
理性的习惯和逻辑的方法,都是可以通过训练来获得的。我们在日常的工作生活中,需要特别重视这样的训练。
小结
当你遇到一个复杂问题的时候,不妨想一想「奥卡姆剃刀」,它就像一个诱发装置,启发你找到更好的解决办法。
如今,我们生活在一个复杂得让人难以理解的世界,但正因为如此,使得「奥卡姆剃刀」成为一个更有价值的思维模型,值得我们好好学习和应用它。
相关文章:

什么是“奥卡姆剃刀”,如何用“奥卡姆剃刀”解决复杂问题?复杂问题简单化
什么是“奥卡姆剃刀”,如何用“奥卡姆剃刀”解决复杂问题?复杂问题简单化问题什么是“奥卡姆剃刀”?如何使用“奥卡姆剃刀”解决问题复杂问题简单化“汉隆剃刀”小结问题 假设你在夜空中看到一颗闪闪发光的「不明飞行物」,你认为这会是什么呢…...
)
角谷定理(递归)
已知有角谷定理: 输入一个自然数,若为偶数,则把它除以2,若为奇数,则把它乘以3加1。经过如此有限次运算后,总可以得到自然数值1。求经过多少次可得到自然数1。如:例如数据22的变化过程ÿ…...
)
数学小课堂:微积分复盘(高等数学本质上是对趋势的动态描述,是对各种相关性抽象的表述。)
文章目录 引言I 复盘1.1 概念和表述1.2 现实与虚构1.3 有穷和无穷1.4 静态和动态1.5 直觉和逻辑II 通过数学逻辑,理解人生。2.1 精明与聪明2.2 朋友和理性的对手2.3 攒钱和赚钱2.4 荣誉和财富引言 高等数学本质上是对趋势的动态描述,是对各种相关性抽象的表述。 I 复盘 1.…...
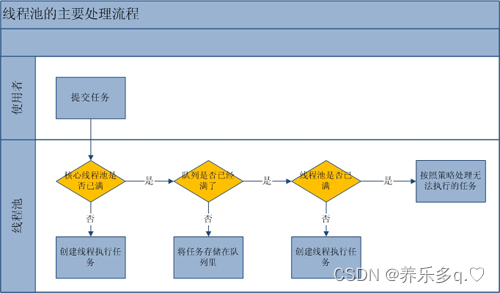
JAVA线程池原理详解一
JAVA线程池原理详解一 一. 线程池的优点 线程是稀缺资源,使用线程池可以减少创建和销毁线程的次数,每个工作线程都可以重复使用。可以根据系统的承受能力,调整线程池中工作线程的数量,防止因为消耗过多内存导致服务器崩溃。 二…...

Windows平台Unity Camera场景实现轻量级RTSP服务和RTMP推送
技术背景随着VR技术在医疗、军事、农业、学校、景区、消防、公共安全、研学机构、展厅展馆,商场等场所普及,开发者对Unity平台下的直播体验提出了更高的要求。技术实现Unity平台下的RTMP推流、RTMP、RTSP播放前几年已经覆盖了Windows、Linux、Android、i…...

LSB 题解
今天来刷一道Misc的题目,LSB原理进行图片隐写 LSB原理 LSB是一种利用人类视觉的局限性设计的幻术 PNG和BMP图片中的图像像素一般是由RGB(RED红 GREEN绿 BLUE蓝)三原色组成 记住,JPG图片是不适合使用LSB隐写的,JPG图片对像数进行了有损压缩…...

离线部署docker与镜像
离线部署docker与镜像 1.离线部署docker 1).在docker官网上下载,合适的安装文件 本次使用的是“docker-20.10.9.tgz ” 下载地址:https://download.docker.com/linux/static/stable/x86_64/ [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下…...
)
Linux文件系统介绍(上)
使用 Linux 系统时,需要作出的决策之一就是为存储设备选用什么文件系统。大多数 Linux 发行版在安装时会非常贴心地提供默认的文件系统,大多数入门级用户想都不想就用了默认的那个。 使用默认文件系统未必就不好,但了解一下可用的选择有时也会…...

创建SpringBoot注意事项
作为一个java小白,你是否因为创建SpringBoot项目那些莫名其妙的错误搞得头皮发麻。不要慌张,这篇文章能帮你解决90%的问题【持续更新…】 本文结合创建SpringBoot项目的完整过程来讲 在idea中新建项目 虽然SpringBoot项目是由maven内核组成的࿰…...

2023年全国最新二级建造师精选真题及答案9
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.关于施工合同违约赔偿损失范围的说法,正确的是()。 A.…...

解决MySQL的 Row size too large (> 8126).
📢欢迎点赞 :👍 收藏 ⭐留言 📝 如有错误敬请指正,赐人玫瑰,手留余香!📢本文作者:由webmote 原创📢作者格言:无尽的折腾后,终于又回到…...

最优传输问题和Sinkhorn
最优传输问题 假设有M堆土,每堆土的大小是ama_mam,有N个坑,每个坑的大小是bnb_nbn,把单位土从土堆m运送到坑n的代价是c(m,n)c(m,n)c(m,n),如何找到一种运输方法填满坑,并且代价最小,这就是…...

Netty核心组件EventLoop源码解析
源码解析目标 分析最核心组件EventLoop在Netty运行过程中所参与的事情,以及具体实现 源码解析 依然用netty包example下Echo目录下的案例代码,单我们写一个NettyServer时候,第一句话就是 EventLoopGroup bossGroup new NioEventLoopGroup(…...

排障命令-汇总
目录 日志查询 1. grep 2. zgrep cpu 1. top 内存 1. free tcp相关 1. netstat 2. ulimit 3. lsof jvm常用 1. jps 2. jinfo 3. jstack 4. jmap 5. jstat 进制转换 1. 十进制转16进制 日志查询 1. grep 定义:(global regular expression) 命令用于查…...

python+pytest接口自动化(4)-requests发送get请求
python中用于请求http接口的有自带的urllib和第三方库requests,但 urllib 写法稍微有点繁琐,所以在进行接口自动化测试过程中,一般使用更为简洁且功能强大的 requests 库。下面我们使用 requests 库发送get请求。requests库简介requests 库中…...

开源电子书工具Calibre 6.3 发布
Calibre 开源项目是 Calibre 官方出的电子书管理工具。它可以查看,转换,编辑和分类所有主流格式的电子书。Calibre 是个跨平台软件,可以在 Linux、Windows 和 macOS 上运行。Calibre 6.3 正式发布,此次更新内容如下:新…...

C++ STL:适配器 Adapter
文章目录1、容器适配器1.1、stack1.2、queue1.3、priority_queue2、迭代器适配器2.1、插入迭代器2.2、反向迭代器2.3、流迭代器3、函数适配器3.1、* bindbind 使用方法bind 简化原理3.2、mem_fn适配器就是接口,对容器、迭代器、算法进行包装,但其实质还是…...

防抖和节流
防抖和节流的区别?防抖:触发高频事件后n 秒内 函数只会执行一次,如果n秒内 高频事件在在次触发,则会重新计算节流:高频事件触发,但在n 秒内 只会执行一次,所以节流会稀释函数的执行频率下面就是…...

vue3 微信扫码登录及获取个人信息实现的三种方法
一、流程: 微信提供的扫码方式有两种,分别是: 跳转二维码扫描页面 内嵌式二维码根据文档我们可以知道关于扫码授权的模式整体流程为: 1. 第三方发起微信授权登录请求,微信用户允许授权第三方应用后,微信会拉起应用或重定向到第三方网站&…...

Java8 新特性强大的Stream API
一、Stream API 说明 Java8中有两大最为重要的改变。第一个是 Lambda 表达式;另外一个则是 Stream API。 Stream API ( java.util.stream) 把真正的函数式编程风格引入到Java中。这是目前为止对Java类库最好的补充,因为Stream API可以极大提供Ja…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
