随机微分方程的MATLAB数值求解

dt=0.01;
tout=200; %总时间为2
x=zeros(1,tout);
x(1)=0.5; %初始位置
mu=0.2; sigma=1;
Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wt
for t=1:tout-1x(t+1)=x(t)+mu*x(t)*dt+sigma*x(t)*Wt(t);
end
t1=1:10:tout; %对原时间序列进行抽样
xt=zeros(1,length(t1));
i=1;
for t=t1xt(i)=0.5*exp((mu-0.5*sigma^2).*dt*t+ ...sigma*sum(Wt(1:t))); %使用理论解对原序列进行抽样计算i=i+1;
end
plot(dt*(1:tout),x,LineWidth=1.5)
hold on
plot(dt*t1,xt,LineWidth=1.5)
hold off
xlabel("$t$",FontSize=20,Interpreter="latex")
dt=0.01;
tout=200;
n=10000;
tends=zeros(1,n);
x=zeros(1,tout);
x(1)=0.1;
mu=0.2; sigma=1;
for k=1:nWt=sqrt(dt)*randn(1,tout); %产生随机序列Wtfor t=1:tout-1x(t+1)=x(t)+mu*x(t)*dt+sigma*x(t)*Wt(t);endtends(k)=x(end);
end
histogram(tends,200)
dt=0.01;
tout=200;
x=zeros(1,tout);
x(1)=0; %初始位置
mu=5; sigma=2;
for i=1:5Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wtfor t=1:tout-1x(t+1)=x(t)-mu*x(t)*dt+sigma*Wt(t);endplot(dt*(1:tout),x,LineWidth=1.5)hold on
end
xlabel("$t$",FontSize=20,Interpreter="latex")
hold off
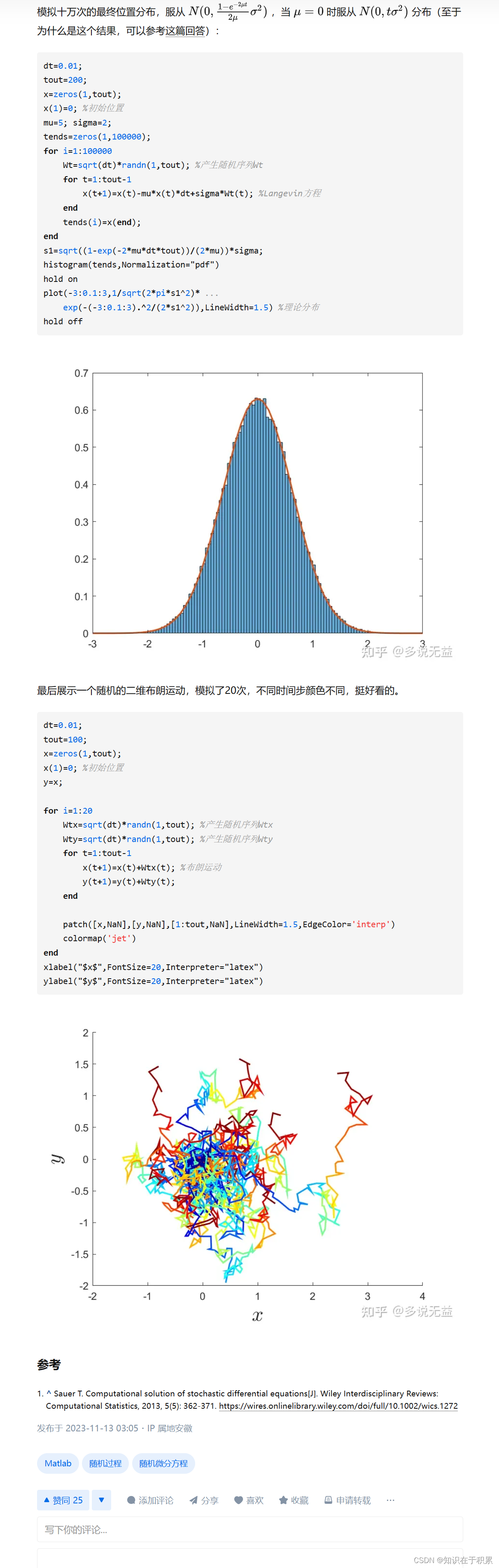
dt=0.01;
tout=200;
x=zeros(1,tout);
x(1)=0; %初始位置
mu=5; sigma=2;
tends=zeros(1,100000);
for i=1:100000Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wtfor t=1:tout-1x(t+1)=x(t)-mu*x(t)*dt+sigma*Wt(t); %Langevin方程endtends(i)=x(end);
end
s1=sqrt((1-exp(-2*mu*dt*tout))/(2*mu))*sigma;
histogram(tends,Normalization="pdf")
hold on
plot(-3:0.1:3,1/sqrt(2*pi*s1^2)* ...exp(-(-3:0.1:3).^2/(2*s1^2)),LineWidth=1.5) %理论分布
hold off
dt=0.01;
tout=100;
x=zeros(1,tout);
x(1)=0; %初始位置
y=x;for i=1:20Wtx=sqrt(dt)*randn(1,tout); %产生随机序列WtxWty=sqrt(dt)*randn(1,tout); %产生随机序列Wtyfor t=1:tout-1x(t+1)=x(t)+Wtx(t); %布朗运动y(t+1)=y(t)+Wty(t);endpatch([x,NaN],[y,NaN],[1:tout,NaN],LineWidth=1.5,EdgeColor='interp')colormap('jet')
end
xlabel("$x$",FontSize=20,Interpreter="latex")
ylabel("$y$",FontSize=20,Interpreter="latex")
^Sauer T. Computational solution of stochastic differential equations[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2013, 5(5): 362-371. https://wires.onlinelibrary.wiley.com/doi/full/10.1002/wics.1272
详见知乎:https://zhuanlan.zhihu.com/p/666480835?utm_campaign=&utm_medium=social&utm_oi=1315073218793488384&utm_psn=1710572578152996864&utm_source=qq
相关文章:

随机微分方程的MATLAB数值求解
dt0.01; tout200; %总时间为2 xzeros(1,tout); x(1)0.5; %初始位置 mu0.2; sigma1; Wtsqrt(dt)*randn(1,tout); %产生随机序列Wt for t1:tout-1x(t1)x(t)mu*x(t)*dtsigma*x(t)*Wt(t); end t11:10:tout; %对原时间序列进行抽样 xtzeros(1,length(t1)); i1; for tt1xt(i)0.5*exp(…...

ChatGPT 也并非万能,品牌如何搭上 AIGC「快班车」
内容即产品的时代,所见即所得,所得甚至超越所见。 无论是在公域的电商平台、社交媒体,还是品牌私域的官网、社群、小程序,品牌如果想与用户发生连接,内容永远是最前置的第一要素。 01 当内容被消费过,就…...

【JavaSE】不允许你不会使用String类
🎥 个人主页:深鱼~🔥收录专栏:JavaSE🌄欢迎 👍点赞✍评论⭐收藏 目录 前言: 一、常用方法 1.1 字符串构造 1.2 String对象的比较 (1)比较是否引用同一个对象 注意…...
身份证阅读器和社保卡读卡器Harmony鸿蒙系统ArkTS语言SDK开发包
项目需求,用ArkTS新一代开发语言实现了在Harmony鸿蒙系统上面兼容身份证阅读器和社保卡读卡器,调用了DonseeDeviceLib.har这个读卡库。 需要注意的是,鸿蒙系统的app扩展名为.hap,本项目编译输出的应用为:entry-default…...

并发与并行
并发和并行是操作系统中的两个重要概念,它们在定义和处理任务的方式上有一些区别。 并发(concurrency)是指在一段时间内,有多个程序都处于启动运行到运行完毕之间,但任一时刻点上只有一个程序在处理机上运行。它是一种…...
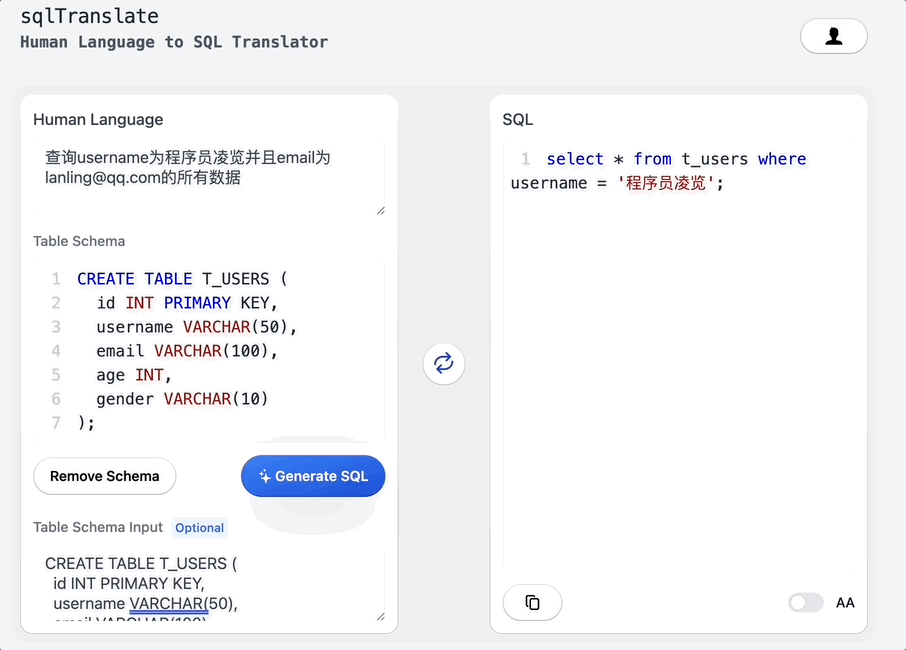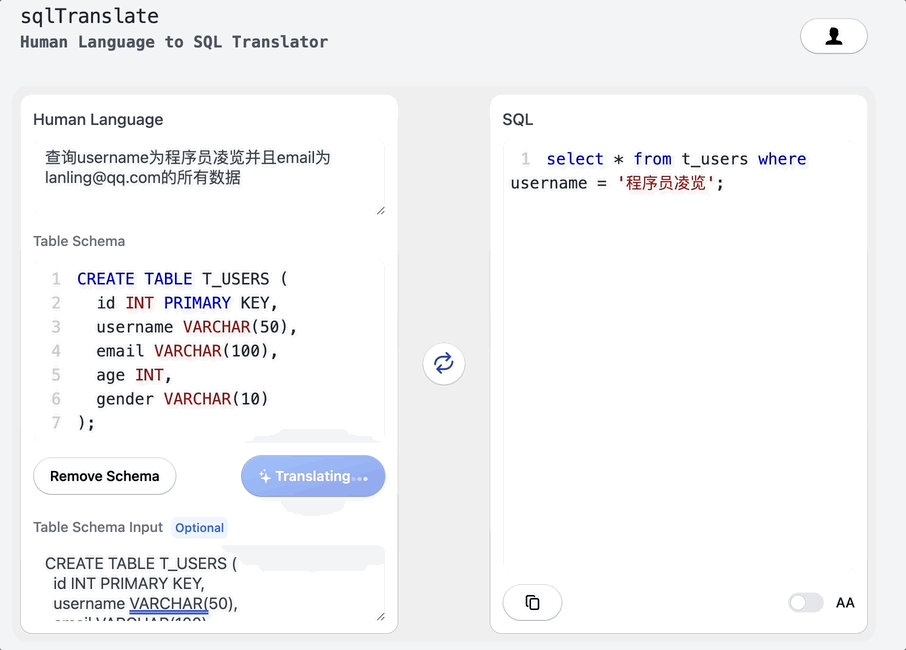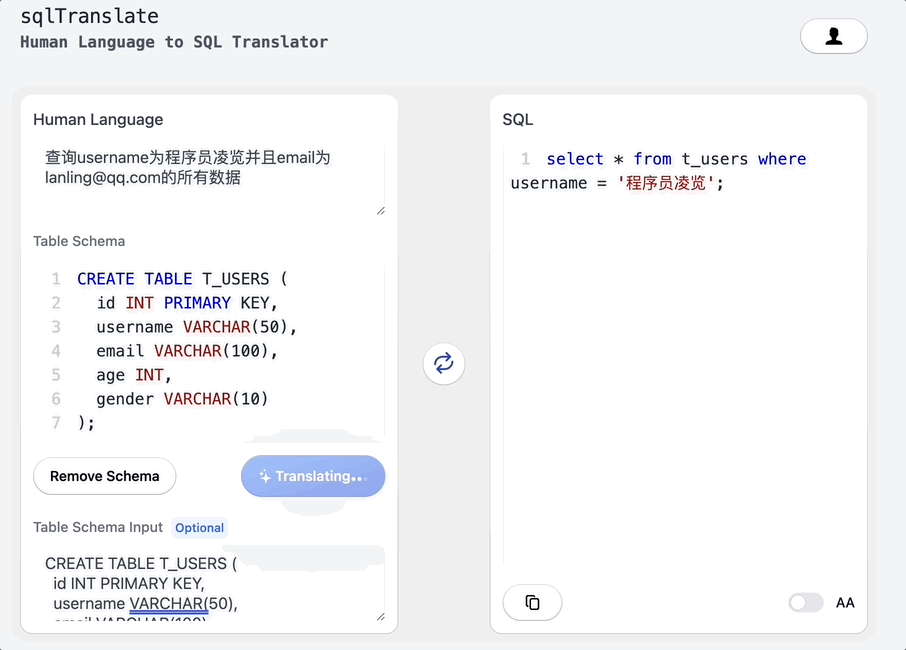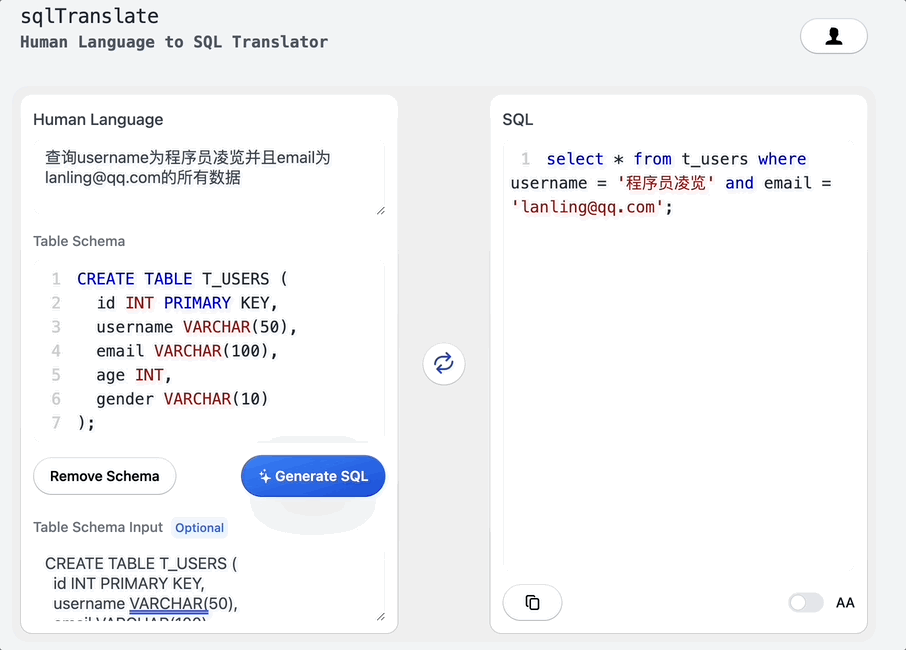
搭个网页应用,让ChatGPT帮我写SQL
大家好,我是凌览。 开门见山,我搭了一个网页应用名字叫sql-translate。访问链接挂在我的个人博客(https://linglan01.cn/about)导航栏,也可以访问https://www.linglan01.cn/c/sql-translate/直达sql-translate。 它的主要功能有:…...

实时云渲染 助力破解智慧园区痛点困局
智慧园区是运用先进的信息技术,如物联网(IoT)、大数据、云计算、人工智能、三维可视化等,对园区内的各类设施、资源以及管理进行智能化和数字化升级。其目标是通过科技手段提升园区的运营效率、资源利用率,提供更便捷、…...

计算机组成原理2
1.浮点数 2.IEEE 754 3.存储器的性能指标 4.存储器的层次化结构 主存类似手机运行内存8g ,辅存类似手机内存128g.... 辅存必须先通过主存才能被cpu接收,就例如微信打开那个月亮小人界面两三秒就是主存在读取辅存的程序然后被cpu接收运行。 5.主存储…...

Py之PyMuPDF:PyMuPDF的简介、安装、使用方法之详细攻略
Py之PyMuPDF:PyMuPDF的简介、安装、使用方法之详细攻略 目录 PyMuPDF的简介 PyMuPDF的安装 PyMuPDF的使用方法 1、基础用法 PyMuPDF的简介 PyMuPDF是一个高性能的Python库,用于PDF(和其他)文档的数据提取,分析,转换和操作。 …...

2023亚太杯数学建模A题B题C题思路模型代码论文指导
2023亚太地区数学建模A题思路:开赛后第一时间更新,获取见文末 名片 2023亚太地区数学建模B题思路:开赛后第一时间更新,获取见文末 名片 2023亚太地区数学建模C题思路:开赛后第一时间更新,获取见文末 名片…...
【C/PTA】函数专项练习(四)
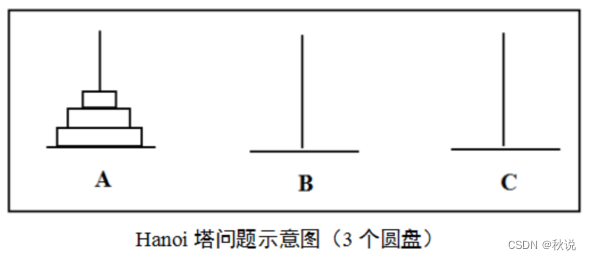
本文结合PTA专项练习带领读者掌握函数,刷题为主注释为辅,在代码中理解思路,其它不做过多叙述。 目录 6-1 计算A[n]1/(1 A[n-1])6-2 递归实现顺序输出整数6-3 自然数的位数(递归版)6-4 分治法求解金块问题6-5 汉诺塔6-6 重复显示字符(递归版)…...

广西柳州机械异形零部件三维扫描3D抄数全尺寸测绘建模-CASAIM中科广电
一、背景介绍 复杂机械异形零部件具有不规则的形状和复杂的结构,给生产制造带来了很大的检测难度。为了确保零部件的制造质量和精度,需要对零部件进行全面的尺寸检测和分析。 CASAIM三维扫描仪在机械异形零部件全尺寸检测应用可以实现对机械异形零部件…...
C语言之符号常量概述)
(四)C语言之符号常量概述
(四)C语言之符号常量概述 一、符号常量概述 一、符号常量概述 在程序中使用像300,20等这样的等类似的“幻数”不是一个好的习惯,它们无法向阅读该程序的人提供更多有用的信息,从而使得修改程序变得困难。处理这种幻数的一种方法是…...

springboot -sse -flux 服务器推送消息
先说BUG处理,遇到提示异步问题 Async support must be enabled on a servlet and for all filters involved in async request processing. This is done in Java code using the Servlet API or by adding "<async-supported>true</async-supported&…...
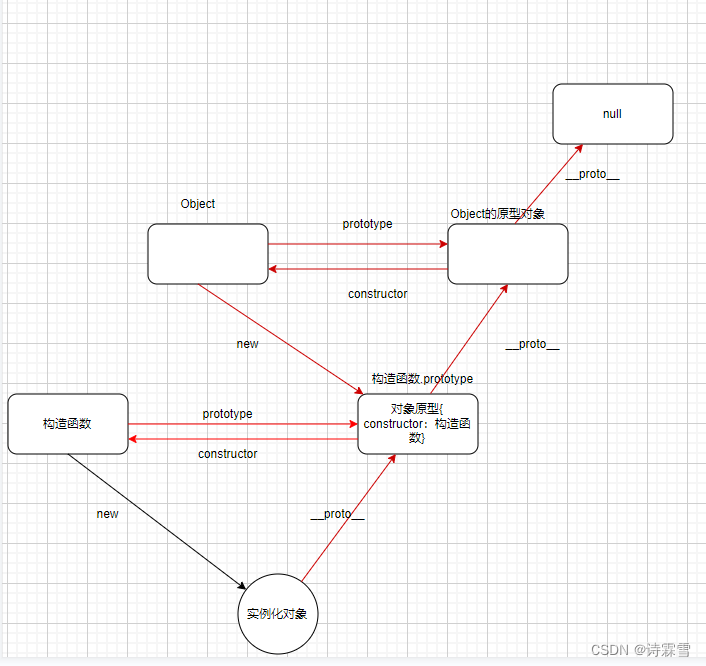
js进阶笔记之原型,原型链
目录 1、原型对象 constructor 属性 对象原型 2、原型链 3、instanceof 4、原型继承 1、原型对象 面向过程就是分析出解决问题所需要的步骤,然后用函数把这些步骤一步一步实现,使用的时候再一个一个的依次调用就可以了。 面向对象是把事务分解成为…...

【DevOps】Git 图文详解(四):Git 使用入门
本系列包含: Git 图文详解(一):简介及基础概念Git 图文详解(二):Git 安装及配置Git 图文详解(三):常用的 Git GUIGit 图文详解(四)&a…...

Jquery ajax 同步阻塞引起的UI线程阻塞的坑(loading图片显示不出来 )
Jquery ajax 同步阻塞引起的UI线程阻塞的坑(loading图片显示不出来,layer.load延迟)jax重新获取数据刷新页面功能,因为ajax属于耗时操作,想在获取数据且加载页面时显示加载遮罩层,结果发现了ajax的好多坑。…...

读书笔记——《黑猩猩的政治》
前言 弗朗斯德瓦尔(Frans de Waal)的代表作《黑猩猩政治》成书于1982年,是它的首部书籍作品,也是美国国会新任议员的被推荐读物。之前看的他另一部作品的《万智有灵》是2016年的作品,时间跨度居然这么大。《万智有灵》介绍了许多…...

此处不允许使用特性namespace
1.DOCTYPE 后面改成 mapper 2.PUBLIC一行中的Config改为Mapper 3.将下一行config变为小写的mapper <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapperPUBLIC "-//mybatis.org//DTD Mapper 3.0//EN""http://mybatis.or…...
随笔记录-springmvc_ResourceHandlerRegistry+ResourceHttpRequestHandler
环境:springboot-2.7.5 配置文件配置静态资源映射 springboot配置静态资源映射方式是通过 WebMvcAutoConfiguration 实现的 spring: # resources: # # 自springboot 2.5.5之后,该属性已经被废弃,使用spring.web.resources.static-locat…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
