平衡二叉树 (简单易懂)
目录
一、概念
二、性质
三、插入操作
四、旋转操作
五、删除操作
六、代码实现
七、复杂度
一、概念
平衡二叉树(Balanced Binary Tree)是一种特殊的二叉搜索树(Binary Search Tree,BST),它在插入和删除节点时通过自平衡的方式来维持树的平衡性。平衡性的维护可以确保树的高度保持在较小的范围内,从而保证了树的基本操作(例如搜索、插入和删除)的平均时间复杂度为 O(log n)。
平衡二叉树的主要特点是任意节点的左子树和右子树的高度差(平衡因子)不超过1。换句话说,对于树中的每个节点,它的左子树和右子树的高度差的绝对值最多为1。
平衡二叉树的平衡性质可以通过旋转操作来维护。旋转操作包括左旋(Left Rotation)、右旋(Right Rotation)、左右旋(Left-Right Rotation)和右左旋(Right-Left Rotation)。这些操作可以使不平衡的树重新平衡,从而确保树的平衡性。
平衡二叉树的优点在于它提供了较快的搜索、插入和删除操作的平均性能,相比于非平衡的二叉搜索树
二、性质
-
二叉搜索树性质: 对于树中的每个节点,其左子树上的所有节点值都小于它,右子树上的所有节点值都大于它。
-
平衡性质: 对于树中的每个节点,它的左子树和右子树的高度差(平衡因子)最多为1。换句话说,任何节点的左右子树高度之差不超过1。
平衡二叉树的平衡性质确保了树的高度始终保持在较小的范围内,从而保持了较快的搜索、插入和删除操作。
三、插入操作
插入一个节点时,首先按照二叉搜索树的规则找到插入位置。然后,从插入位置向上回溯,更新每个祖先节点的高度,并检查平衡性质是否被破坏。如果发现某个节点的平衡因子超过1或小于-1,需要通过旋转操作来修复平衡性。
四、旋转操作
平衡二叉树的旋转操作有四种:左旋、右旋、左右旋、右左旋。这些旋转操作可以将不平衡的树重新平衡。下面简要介绍左旋和右旋:
-
左旋(LL旋转): 当一个节点的右子树比左子树高度高,且右子树的左子树高度不低于右子树的右子树时,进行左旋。左旋是通过将当前节点的右子树提升为新的根,并将原根作为新根的左子树来实现的。
-
右旋(RR旋转): 当一个节点的左子树比右子树高度高,且左子树的右子树高度不低于左子树的左子树时,进行右旋。右旋是通过将当前节点的左子树提升为新的根,并将原根作为新根的右子树来实现的。
五、删除操作
删除节点时,首先按照二叉搜索树的规则找到要删除的节点。删除节点后,从删除位置向上回溯,更新每个祖先节点的高度,并检查平衡性质是否被破坏。如果发现某个节点的平衡因子超过1或小于-1,同样需要通过旋转操作来修复平衡性。
六、代码实现
class TreeNode {int val;int height; // 节点的高度TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;this.height = 1;this.left = null;this.right = null;}
}public class AVLTree {private TreeNode root;public AVLTree() {this.root = null;}// 获取节点高度private int height(TreeNode node) {return (node == null) ? 0 : node.height;}// 更新节点高度private void updateHeight(TreeNode node) {if (node != null) {node.height = 1 + Math.max(height(node.left), height(node.right));}}// 获取平衡因子private int getBalanceFactor(TreeNode node) {return (node == null) ? 0 : height(node.left) - height(node.right);}// 左旋private TreeNode leftRotate(TreeNode y) {TreeNode x = y.right;TreeNode T2 = x.left;// 执行旋转x.left = y;y.right = T2;// 更新高度updateHeight(y);updateHeight(x);return x;}// 右旋private TreeNode rightRotate(TreeNode x) {TreeNode y = x.left;TreeNode T2 = y.right;// 执行旋转y.right = x;x.left = T2;// 更新高度updateHeight(x);updateHeight(y);return y;}// 插入节点public TreeNode insert(TreeNode root, int val) {if (root == null) {return new TreeNode(val);}// 执行标准的BST插入if (val < root.val) {root.left = insert(root.left, val);} else if (val > root.val) {root.right = insert(root.right, val);} else {// 不允许插入相同的值return root;}// 更新节点高度updateHeight(root);// 获取平衡因子int balance = getBalanceFactor(root);// 平衡维护// 左子树高度大于右子树,且插入发生在左子树的左侧,需要进行右旋if (balance > 1 && val < root.left.val) {return rightRotate(root);}// 右子树高度大于左子树,且插入发生在右子树的右侧,需要进行左旋if (balance < -1 && val > root.right.val) {return leftRotate(root);}// 左子树高度大于右子树,且插入发生在左子树的右侧,需要先左旋再右旋if (balance > 1 && val > root.left.val) {root.left = leftRotate(root.left);return rightRotate(root);}// 右子树高度大于左子树,且插入发生在右子树的左侧,需要先右旋再左旋if (balance < -1 && val < root.right.val) {root.right = rightRotate(root.right);return leftRotate(root);}return root;}// 对外提供的插入接口public void insert(int val) {root = insert(root, val);}// 中序遍历private void inOrderTraversal(TreeNode root) {if (root != null) {inOrderTraversal(root.left);System.out.print(root.val + " ");inOrderTraversal(root.right);}}// 对外提供的中序遍历接口public void inOrderTraversal() {inOrderTraversal(root);}public static void main(String[] args) {AVLTree avlTree = new AVLTree();// 插入一些节点进行测试avlTree.insert(10);avlTree.insert(20);avlTree.insert(30);avlTree.insert(15);avlTree.insert(5);// 中序遍历,检查树的平衡性avlTree.inOrderTraversal();}
}
七、复杂度
平衡二叉树的高度始终保持在O(log n)范围内,因此搜索、插入和删除操作的平均时间复杂度为O(log n)。
总之,平衡二叉树通过维护平衡性质,提高了搜索、插入和删除操作的效率,确保树的高度保持在较小范围内。
相关文章:
)
平衡二叉树 (简单易懂)
目录 一、概念 二、性质 三、插入操作 四、旋转操作 五、删除操作 六、代码实现 七、复杂度 一、概念 平衡二叉树(Balanced Binary Tree)是一种特殊的二叉搜索树(Binary Search Tree,BST),它在插入和…...

Vue.observable 是什么
Observable 翻译过来我们可以理解成可观察的 Vue.js2.6 新增 Vue.observable,让一个对象变成响应式数据。Vue 内部会用它来处理 data 函数返回的对象 。 返回的对象可以直接用于渲染函数和计算属性内,并且会在发生变更时触发相应的更新。也可以作为最小化…...

【五年创作纪念日】
机缘 我成为创作者的过程并不复杂,可以说是一个自然的发展。我是一名软件工程师,日常的工作主要是编程和解决问题。在工作的过程中,我发现有很多时候我需要查找一些特定的技术问题或者寻找一些最佳实践来解决我遇到的问题。在这个过程中&…...

数据库基础入门 — SQL排序与分页
我是南城余!阿里云开发者平台专家博士证书获得者! 欢迎关注我的博客!一同成长! 一名从事运维开发的worker,记录分享学习。 专注于AI,运维开发,windows Linux 系统领域的分享! 本…...
WordPress站点屏蔽过滤垃圾评论教程(Akismet反垃圾评论插件)
前段时间我的WordPress站点经常收到垃圾评论的轰炸,严重时一天会收到几十条垃圾评论。我这个小破站一没啥流量,二又不盈利,实在是不太理解为啥有人要这么执着地浪费资源在上面。 Akismet反垃圾评论插件 其实用了 Akismet 反垃圾评论插件后&a…...
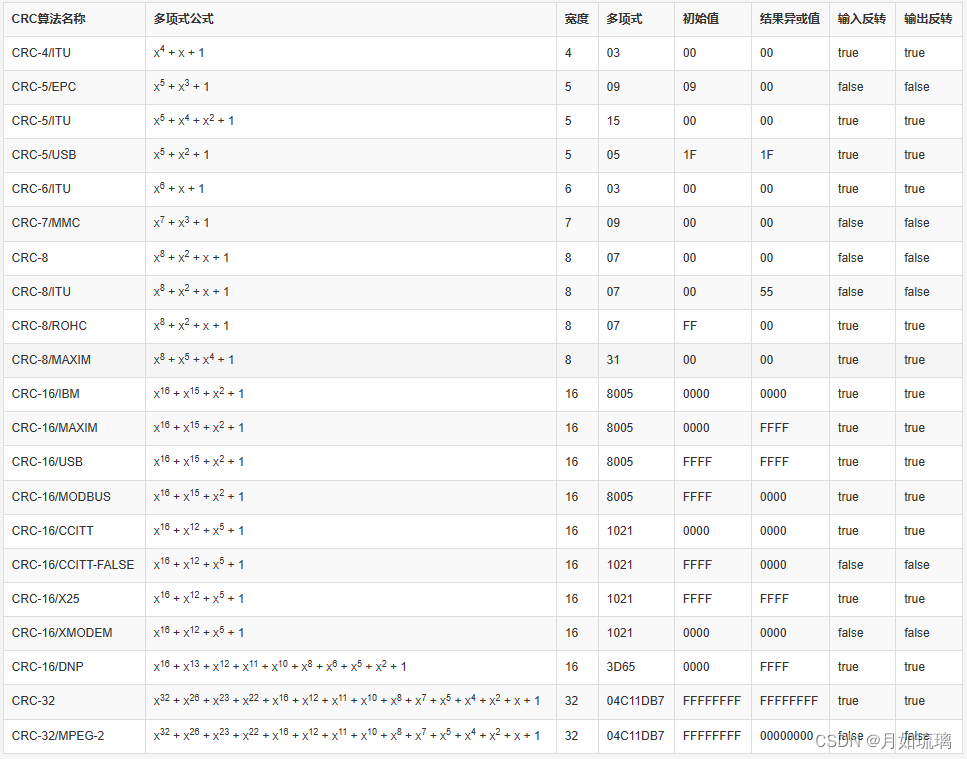
Modbus-RTU协议讲解与实战
1、背景 工作需要,需要使用Modbus-RTU实现RS485通信,于是简单学习并实践了一下。 2、参考资料 一文看懂Modbus协议 3、协议说明 3.1、协议类型 当前设备采用Modbus-RTU协议,采用CRC-16_Modbus校验算法,数据链路层使用用标准串口协议,物理层采用RS485进行数据传输。 …...

数据结构 查找基本概念
敬请期待。。。 1. 适用于折半查找的表的存储方式及元素排列要求为(顺序方式存储,元素有序 )。 2. 有一个按元素值排好序的顺序表(长度大于2),分别用顺序查找和折半查找与给定值相等的元素,比较次数分别是s和b&am…...
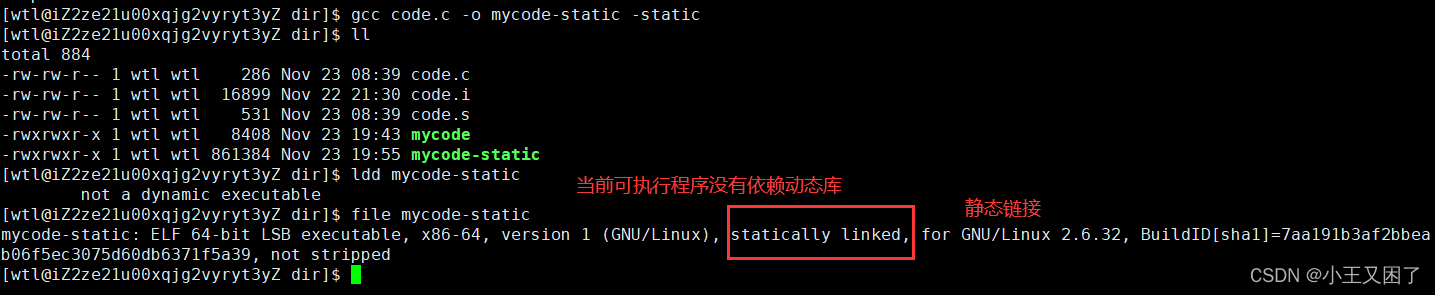
『Linux升级路』基础开发工具——gcc/g++篇
🔥博客主页:小王又困了 📚系列专栏:Linux 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、快速认识gcc/g 二、预处理 📒1.1头文件展开 📒1…...

面试:RocketMQ相关问题
文章目录 什么是 RocketMQ,有哪些使用场景?RocketMQ 由哪些⻆色组成,每个⻆色作用和特点是什么?RocketMQ 中的 Topic 和 JMS 的 queue 有什么区别?RocketMQ 消费模式有几种?RocketMQ 的 Consumer 是如何消费…...
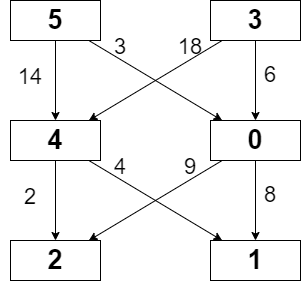
2304. 网格中的最小路径代价 : 从「图论最短路」过渡到「O(1) 空间的原地模拟」
题目描述 这是 LeetCode 上的 「2304. 网格中的最小路径代价」 ,难度为 「中等」。 Tag : 「最短路」、「图」、「模拟」、「序列 DP」、「动态规划」 给你一个下标从 0 开始的整数矩阵 grid,矩阵大小为 m x n,由从 0 到 的不同整数组成。 你…...
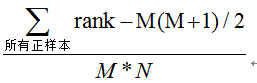
【机器学习】算法性能评估常用指标总结
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive࿰…...

前端 JavaScript 与 HTML 怎么实现交互?
前端的交互性是通过JavaScript与HTML结合实现的。JavaScript作为一种脚本语言,可以嵌入HTML中,通过对DOM(文档对象模型)的操作,实现与用户的交互。以下将详细介绍前端JavaScript与HTML如何实现交互,包括事件…...
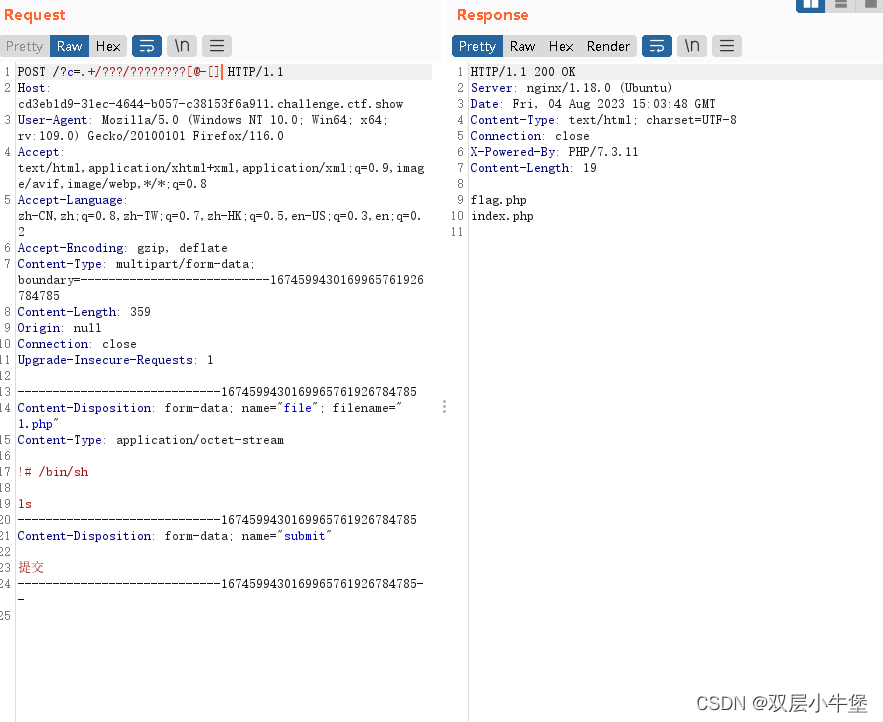
命令执行总结
之前做了一大堆的题目 都没有进行总结 现在来总结一下命令执行 我遇到的内容 这里我打算按照过滤进行总结 依据我做过的题目 过滤system 下面是一些常见的命令执行内容 system() passthru() exec() shell_exec() popen() proc_open() pcntl_exec() 反引号 同shell_exec() …...
)
机器学习——词向量模型(CBOW代码实现-未开始)
本来是不打算做这个CBOW代码案例的,想快马加鞭看看前馈神经网络 毕竟书都买好了 可是…可是…我看书的时候,感觉有点儿困难,哭的很大声… 感觉自己脑细胞可能无法这么快接受 要不,还是退而求个稍微难度没那么大的事,想…...

智慧海岛/海域方案:助力海洋空间智慧化、可视化管理
随着我国海洋经济的快速发展,海域海岛的安防技术也获得了进步。传统的安防监控模式已经满足不了海域海岛的远程监管需求。伴随着人工智能、边缘计算、大数据、通信传输技术、视频技术、物联网等信息化技术的发展,海岛海域在监管手段上,也迎来…...

Bin、Hex、ELF、AXF的区别
1.Bin Bin文件是最纯粹的二进制机器代码, 或者说是"顺序格式"。按照assembly code顺序翻译成binary machine code,内部没有地址标记。Bin是直接的内存映象表示,二进制文件大小即为文件所包含的数据的实际大小。 BIN文件就是直接的二进制文件&…...
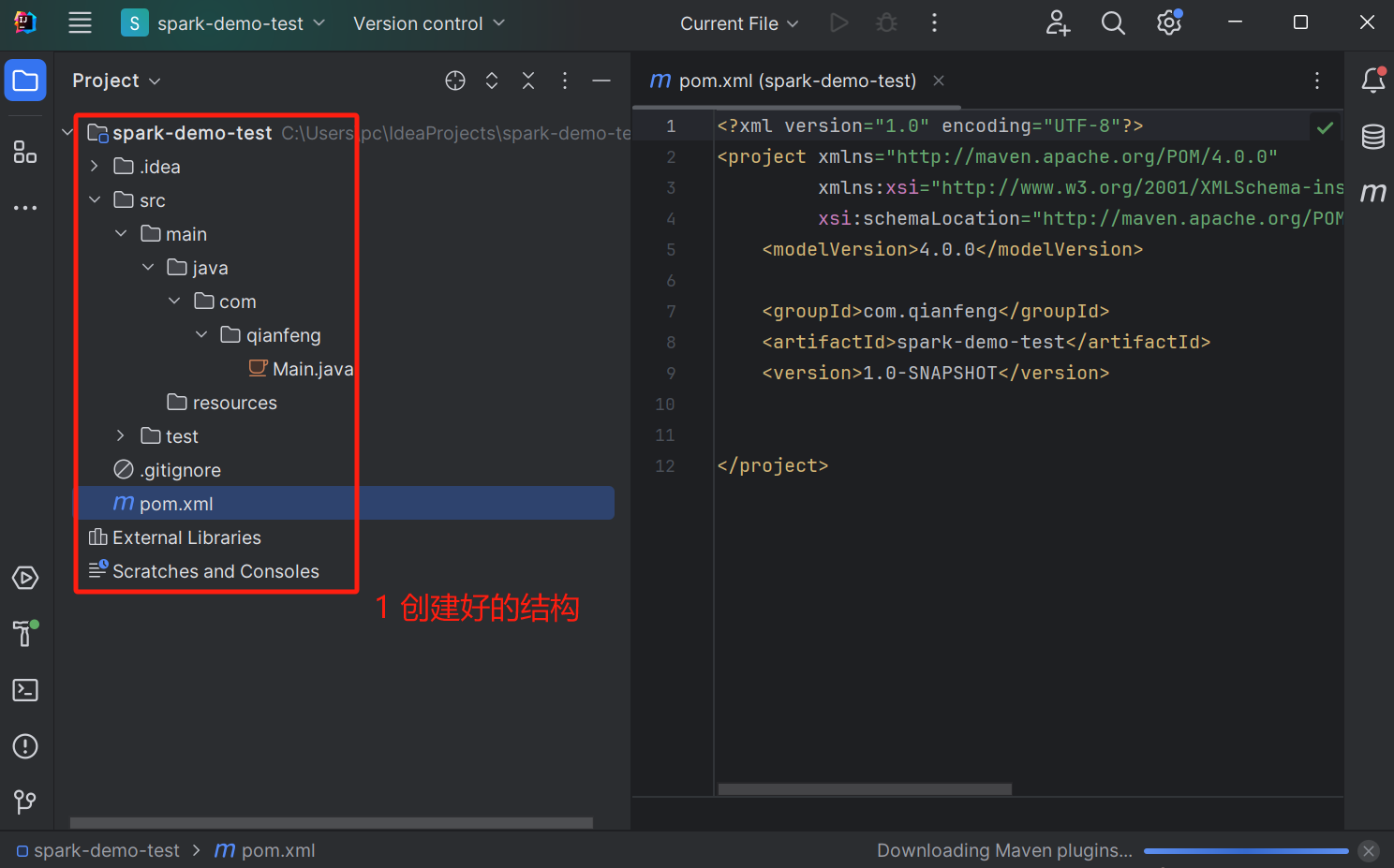
IDEA安装教程
文章目录 1 下载IntelliJ IDEA2 安装3 IDEA配置4 创建项目 1 下载IntelliJ IDEA 官方网站上下载最新版本的IntelliJ IDEA。官方网站提供了两个版本:Community版和Ultimate版。 Community版是免费的,适用于个人和非商业用途。Ultimate版则需要付费购…...
DRF-项目-(1):构建纯净版的drf项目,不再使用django的后台管理,django的认证,django的session等功能,作为一个纯接口项目
项目的目录结构: -HeartFailure |-- apps |--user |--HeartFailure |-- static |--manage.py 一、django项目相关的 1、命令行中创建django项目 #1、切换到指定的虚拟环境中 workon my_drf#2、该虚拟环境已经安装好django和rest_framework了 django-admin startp…...

ubuntu 手动清理内存cache
/proc是一个虚拟文件系统,我们可以通过对它的读写操作来做为与kernel实体间进行通信的一种手段。也就是说可以通过修改/proc中的文件,来对当前kernel的行为做出调整。 那么我们可以通过调整/proc/sys/vm/drop_caches来释放内存。操作如下: …...
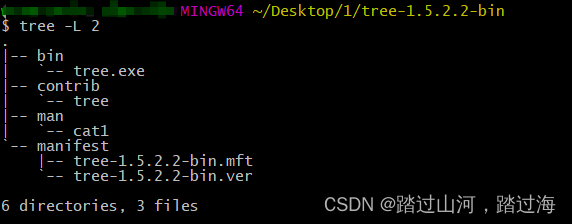
gitBash中如何使用Linux中的tree命令
文章目录 在gitBash中安装tree的目的如何安装安装完成,就可以直接完美适配Linux系统了 在gitBash中安装tree的目的 如下图,powershell虽然可以看做是window下的Linux系统,但是根本就不适配很多Linux中的命令 如何安装 tree.exe安装网址 下载 tree 命令的 二进制包…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
