常见立体几何图形的体积
文章目录
- abstract
- 祖暅原理
- 推论
- 棱锥和圆锥的体积
- 用积分的方法推导
- 棱台和圆台的体积
- 圆台体积公式
- 球体的体积
- 球体的表面积
abstract
- 锥体和球体的体积公式主要通过积分的方法推导
- 这类公式的推导中学一般不要求,只要会应用公式
- 在高等数学中由合适和方便的工具来推导这些公式
- 而相关的衍生几何体例如台体体积,可以用割补法直接推导
- 而中学中一个重要原理是祖暅原理,利用该原理可以确定或间接得到许多几何体体积公式
祖暅原理
- 祖暅原理指出:幂势既同,则积不容异
- 这句话是说,加载两个平行平面简的两个几何体,被平行于这两个平面的任意平面所截,若所截的两个截面的面积相等,那么这两个几何体的体积相等
- 简单讲就是:若两物体在任意等高处的截面面积始终相等,则两个物体体积相等
- 例如,取一摞纸对方在桌面上,将它们扭转一定的角度,得到一个不规则的体积,但我们知道,扭转前后这些纸构成的立体体积保持不变,因为高度保持不变,同一水平截面积相同,因此体积相同(祖暅原理)
推论
-
祖暅原理可以说明,等底面积,等高的两个柱体或锥体的体积相等
- 因此,无论是直棱柱还是斜棱柱,当它们的底面积和高都分别相等,则体积也相等
- 因此只要知道柱体的底面积和高就可以求出柱体体积
棱锥和圆锥的体积
-
在小学我们通过比较容积的方法,验证了圆锥的体积是等底面积,等高的圆柱体的 1 3 \frac{1}{3} 31
-
事实上,用同样体积的三个三棱锥 V 1 , V 2 , V 3 V_1,V_2,V_3 V1,V2,V3能够补成一个三棱柱 V V V(若 V 0 V_0 V0是斜棱锥,那么 V V V是斜棱柱)
- 三棱柱有6个顶点,上底面和下地面各3个点,使用的 V 1 , V 2 , V 3 V_1,V_2,V_3 V1,V2,V3存在相等的三角形面,例如 V 1 , V 2 V_1,V_2 V1,V2其中一个不含底面,拼接后得到5个顶点的多面体,再拼接 V 3 V_3 V3得到一个三棱柱
- 这并不是说三棱柱都可以分割成完全相同的三个棱锥
- 例如一个非常细长的三棱柱,则按对角线分割后,有上下底面的两个三棱锥完全相同,但是第三个明显与前者不同
-
再根据祖暅原理,可以说明三棱锥的体积是等面积,等高的三棱柱体积的三分之一
-
在此基础上,可以推出锥体体积的计算公式:若锥体(包括棱锥和圆锥)底面积为 S S S,高为 h h h,则体积 V = 1 3 S h V=\frac{1}{3}Sh V=31Sh
(0)
用积分的方法推导
-
一个 n n n棱锥可以通过分割转化为三棱锥问题
-
设,三棱锥的底面积为 S 0 S_0 S0,高为 h h h
- 设棱锥的高对应的线段,起点为棱锥顶点 A A A,投影到底面 B B B
- 取 A B AB AB上的一点 C C C,记 h = A B , h ′ = A C h=AB,h'=AC h=AB,h′=AC, k = A C A B k=\frac{AC}{AB} k=ABAC= h ′ h \frac{h'}{h} hh′
(1),
k ∈ [ 0 , 1 ] k\in[0,1] k∈[0,1] - 则过点 C C C垂直于 A B AB AB的平面截棱锥得到截面 S 1 S_{1} S1= k 2 S 0 k^2S_0 k2S0
(2) - 将(1)代入(2),得 S 1 = h ′ 2 h 2 S 0 S_1=\frac{h'^2}{h^2}S_0 S1=h2h′2S0
(3),所以棱锥体积为 ∫ 0 h S 1 d h ′ \int_{0}^{h}S_1\mathrm{d}h' ∫0hS1dh′= ∫ 0 h h ′ 2 h 2 S 0 d h ′ \int_{0}^{h}\frac{h'^2}{h^2}S_0\mathrm{d}h' ∫0hh2h′2S0dh′= S 0 h 2 ∫ 0 h h ′ 2 d h ′ \frac{S_0}{h^2}\int_{0}^{h}h'^2\mathrm{d}h' h2S0∫0hh′2dh′= S 0 h 2 ⋅ 1 3 h ′ 3 ∣ 0 h \frac{S_0}{h^2}\cdot{\frac{1}{3}h'^3}|_{0}^{h} h2S0⋅31h′3∣0h= 1 3 S 0 h \frac{1}{3}S_0h 31S0h(4)
-
对于圆锥也是类似的
-
综上,我们有任意锥体公式,即式(0)
棱台和圆台的体积
- 棱台是由棱锥被一个平行于底面的平面截取一个锥体得到的立体图形,圆台类似
- 因此,台体的体可以用2个椎体的体积只差计算
- 设棱台的上下底面面积分别为 S ′ , S S',S S′,S;而台体的高为 h h h
- 设台体由棱锥 V 1 V_1 V1被平面截取所得包含原底面的部分,而另一部分是包含顶点的锥体 V 2 V_2 V2,设其高度为 t t t,则 V V V的高度为 t + h t+h t+h
- 从而台体的体积 V = V 1 − V 2 V=V_1-V_2 V=V1−V2= 1 3 S ( t + h ) − 1 3 S ′ t \frac{1}{3}S(t+h)-\frac{1}{3}S't 31S(t+h)−31S′t
(5) - 而由几何平行于相似的知识可知若设 t t + h \frac{t}{t+h} t+ht= k k k
(6), ( k > 0 ) (k>0) (k>0),则 S ′ S = k 2 \frac{S'}{S}=k^2 SS′=k2(7),即 k = S ′ / S k=\sqrt{S'/S} k=S′/S(8) - 联立(7,8)可以求得 t t t= h ( 1 1 − S ′ / S − 1 ) h(\frac{1}{1-\sqrt{S'/S}}-1) h(1−S′/S1−1)= h S ′ + S ′ S S − S ′ h\frac{S'+\sqrt{S'S}}{S-S'} hS−S′S′+S′S
(9) - 将(9)代入(5):
- 1 3 ( S t + S h − S ′ t ) \frac{1}{3}(St+Sh-S't) 31(St+Sh−S′t)= 1 3 ( S h + ( S − S ′ ) t ) \frac{1}{3}(Sh+(S-S')t) 31(Sh+(S−S′)t)= 1 3 ( S h + ( S − S ′ ) h S ′ + S ′ S S − S ′ ) \frac{1}{3}(Sh+(S-S')h\frac{S'+\sqrt{S'S}}{S-S'}) 31(Sh+(S−S′)hS−S′S′+S′S)= 1 3 h ( S + S ′ + S ′ S ) \frac{1}{3}h(S+S'+\sqrt{S'S}) 31h(S+S′+S′S)
(10)
- 1 3 ( S t + S h − S ′ t ) \frac{1}{3}(St+Sh-S't) 31(St+Sh−S′t)= 1 3 ( S h + ( S − S ′ ) t ) \frac{1}{3}(Sh+(S-S')t) 31(Sh+(S−S′)t)= 1 3 ( S h + ( S − S ′ ) h S ′ + S ′ S S − S ′ ) \frac{1}{3}(Sh+(S-S')h\frac{S'+\sqrt{S'S}}{S-S'}) 31(Sh+(S−S′)hS−S′S′+S′S)= 1 3 h ( S + S ′ + S ′ S ) \frac{1}{3}h(S+S'+\sqrt{S'S}) 31h(S+S′+S′S)
- 公式(10)就是台体的体积公式
圆台体积公式
- 当圆台的上下底面的半径分别为 r ′ , r r',r r′,r,高为 h h h,则它的体积为 V = 1 3 π h ( r 2 + r r ′ + r ′ 2 ) V=\frac{1}{3}{\pi}h(r^2+rr'+r'^2) V=31πh(r2+rr′+r′2)
球体的体积
- 设球的半径为 R R R,则其体积为 4 3 π R 3 \frac{4}{3}\pi{R^3} 34πR3
- 球体的体积可以基于牟合方盖和祖暅原理以及锥体体积公式得到
- 但是过程较为繁琐,如果使用积分的方法,可以简单的推出这个公式
- 积分的方法推导
- 球体可以理解为半圆旋转一周得到的立体图形
- 在直角坐标系上做半径为 R R R,圆心为原点的圆,并只取其在第一象限内的部分( 1 4 \frac{1}{4} 41圆),记为曲线 C C C, x 2 + y 2 = R 2 x^2+y^2=R^2 x2+y2=R2,即 y = R 2 − x 2 y=\sqrt{R^2-x^2} y=R2−x2, ( x , y ⩾ 0 ) (x,y\geqslant{0}) (x,y⩾0)
- 令 C C C绕着 x x x轴旋转一周,得到半球记为 V 0 V_0 V0,我们先求 V 0 V_0 V0的体积(仍然记为 V 0 V_0 V0)
- 用空间平面 x = x 0 x=x_0 x=x0(垂直于 x x x轴的平面)截取 V 0 V_0 V0的截面面积为 S ( x ) S(x) S(x)= π y 2 \pi{y^2} πy2= π ( R 2 − x 2 ) \pi(R^2-x^2) π(R2−x2)
- V 0 V_{0} V0= ∫ 0 R S ( x ) d x \int_{0}^{R}S(x)\mathrm{d}x ∫0RS(x)dx= π ∫ 0 R R 2 − x 2 d x \pi\int_{0}^{R}R^2-x^2\mathrm{d}x π∫0RR2−x2dx= π ( R 3 − 1 3 R 3 ) \pi(R^3-\frac{1}{3}R^3) π(R3−31R3)= 2 3 π R 3 \frac{2}{3}{\pi}R^3 32πR3
- 从而 V = 2 V 0 V=2V_0 V=2V0= 4 3 π R 3 \frac{4}{3}\pi{R^3} 34πR3
- 事实上可以直接用旋转体积中绕 x x x轴旋转的立体图形的体积公式: V 0 V_0 V0= π ∫ 0 R y 2 d x \pi\int_{0}^{R}y^2\mathrm{d}x π∫0Ry2dx= 2 3 π R 3 \frac{2}{3}\pi{R^3} 32πR3
- 还可以借助三重积分(令积分区域为球,被积函数为1)在球坐标上的计算方法来求解球的体积 V V V= ∫ 0 2 π d θ ∫ 0 π d ϕ ∫ 0 a ( 1 r 2 sin ϕ ) d r \int_{0}^{2\pi}\mathrm{d}\theta\int_{0}^{\pi}\mathrm{d}\phi\int_{0}^{a} (1r^2\sin\phi) \mathrm{d}r ∫02πdθ∫0πdϕ∫0a(1r2sinϕ)dr= ∫ 0 2 π d θ ∫ 0 π sin ϕ d ϕ ∫ 0 a 1 r 2 d r \int_{0}^{2\pi}\mathrm{d}\theta\int_{0}^{\pi}\sin\phi\mathrm{d}\phi\int_{0}^{a} 1r^2\mathrm{d}{r} ∫02πdθ∫0πsinϕdϕ∫0a1r2dr= 2 π ⋅ 2 ⋅ a 3 3 2\pi\cdot{2}\cdot{\frac{a^3}{3}} 2π⋅2⋅3a3= 4 3 π a 3 \frac{4}{3}\pi{a^3} 34πa3
球体的表面积
-
利用球体的体积和微积分思想,可以求出半径为 R R R的球体的表面积为 4 π R 2 4\pi{R^2} 4πR2
-
将球面微分成个 n ( n → ∞ ) n(n\to{\infin}) n(n→∞)小区域,每个小区域边缘和球心连线近似为一个锥体,将求的表面积设为 S S S,则 1 3 S R \frac{1}{3}S{R} 31SR= 4 3 π R 3 \frac{4}{3}\pi{R^3} 34πR3,解得 S = 4 π R 2 S=4\pi{R^2} S=4πR2
相关文章:

常见立体几何图形的体积
文章目录 abstract祖暅原理推论 棱锥和圆锥的体积用积分的方法推导棱台和圆台的体积圆台体积公式 球体的体积球体的表面积 abstract 锥体和球体的体积公式主要通过积分的方法推导 这类公式的推导中学一般不要求,只要会应用公式在高等数学中由合适和方便的工具来推导这些公式而…...

vue3 + vue-router + keep-alive缓存页面
1.vue-router中增加mate.keepAlive和deepth属性 {path: /,name: home,component: HomeView,meta: {// 当前页面要不要缓存keepAlive: false,// 当前页面层级deepth: 1,}},{path: /list,name: list,component: ListView,meta: {// 当前页面要不要缓存keepAlive: true,// 当前页…...
unigui同页面内重定向跳转,企业微信内部应用开发获取用户code例子
procedure TMainForm.UniFormCreate(Sender: TObject); varurl: string;code: string; begin //如果没有code值,将进行重定向if UniApplication.Parameters.Values[code] thenbeginurl :https://open.weixin.qq.com/connect/oauth2/authorize?appid你们的企业ID&…...

垃圾数据啊
const arr [] //定义空数组 for (const key in this.fgkSyData) { //循环 this。sgksudata 数据arr.push( //push添加到 arr { [key]:this.fgkSyData[key] } //{} 在对象中 重新 定义key value 转换成对象) } console.log(arr, arr) …...

GB/T 29498-2013 木门窗检测
木门窗是指以木材、木质复合材料为主要材料制作框和扇的门窗。 GB/T 29498-2013 木门窗检测项目 测试项目 测试标准 外观质量 GB/T 29498 尺寸 GB/T 29498 装配质量 GB/T 29498 含水率 GB/T 17657 附着力 GB/T 4893.4 外门窗耐冷热循环 GB/T 4893.7 耐划痕 GB/…...

rocketMQ5.0顺序消息golang接入
本人理解,顺序消息如果不分消息组,那么会影响并行处理速度,所以尽量消息组分的散一些 首先上要求,官方文档如下: 总结: 1.必须同一个消息组,消息组和消费组不是一个概念,不要混 2.必…...

HuggingFace-利用BERT预训练模型实现中文情感分类(下游任务)
准备数据集 使用编码工具 首先需要加载编码工具,编码工具可以将抽象的文字转成数字,便于神经网络后续的处理,其代码如下: # 定义数据集 from transformers import BertTokenizer, BertModel, AdamW # 加载tokenizer token Ber…...
PSP - 从头搭建 抗原类别 (GPCR) 的 蛋白质结构预测 项目流程
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/134595717 GPCRs(G Protein-Coupled Receptors,G蛋白偶联受体),又称为7次跨膜受体,是细…...

城市NOA加速落地,景联文科技高质量数据标注助力感知系统升级
当前,自动驾驶技术的演进正在经历着从基础L2到L3过渡的重要阶段,其中NOA(自动辅助导航驾驶)扮演着至关重要的角色。城市NOA(L2.9)作为城市场景下的NOA,被看作是车企向更高阶自动驾驶迈进的必经之…...
是什么?)
控制反转(IoC)是什么?
文章目录 控制反转(Inversion of Control,IoC)传统的程序设计中:应用程序控制程序流程控制反转设计中:由框架或容器控制程序流程IoC 的作用 举例生活例子软件工程例子 控制反转(Inversion of Control&#…...

Redisson分布式锁源码解析、集群环境存在的问题
一、使用Redisson步骤 Redisson各个锁基本所用Redisson各个锁基本所用Redisson各个锁基本所用 二、源码解析 lock锁 1) 基本思想: lock有两种方法 一种是空参 另一种是带参 * 空参方法:会默认调用看门狗的过期时间30*1000&…...

2016年10月4日 Go生态洞察:HTTP追踪介绍
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

分布式篇---第四篇
系列文章目录 文章目录 系列文章目录前言一、分布式ID生成有几种方案?二、幂等解决方法有哪些?三、常见负载均衡算法有哪些?前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给…...
从零开始的C++(十九)
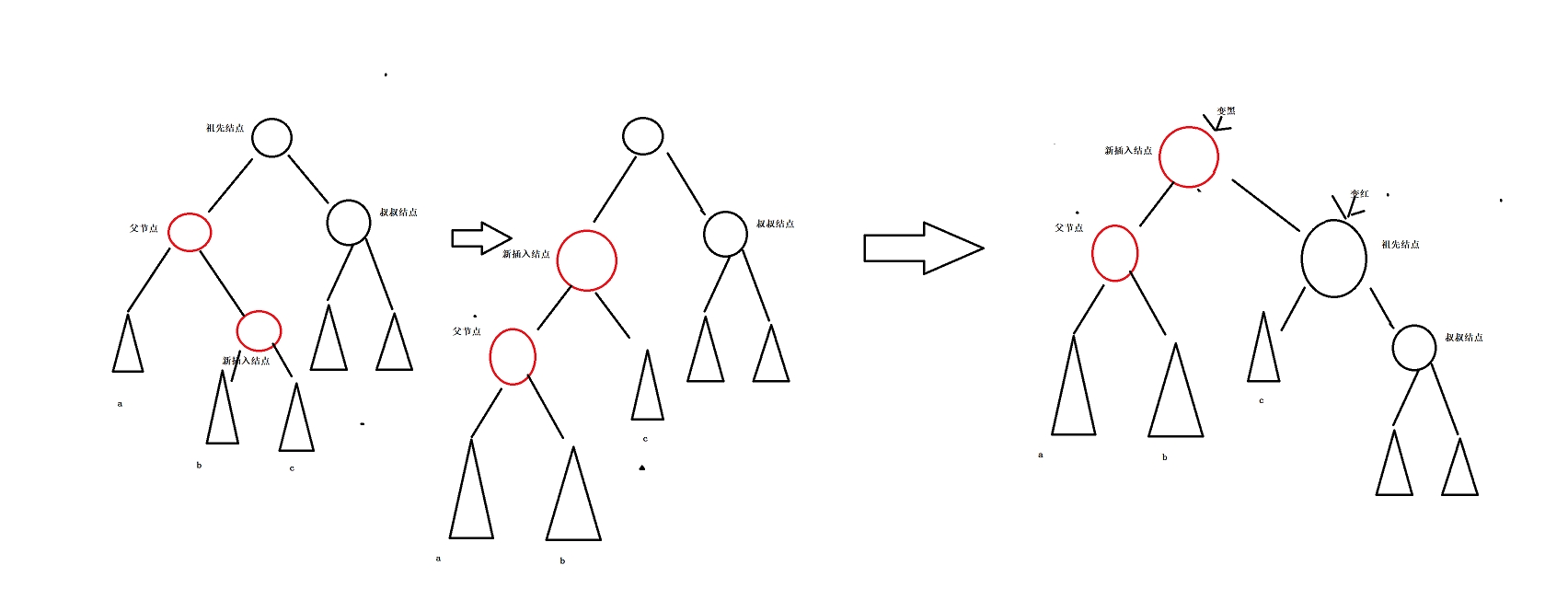
红黑树: 一种接近平衡的二叉树,平衡程度低于搜索二叉树。 特点: 1.根节点为黑 2.黑色结点的子结点可以是红色结点或黑色结点。 3.红色结点的子结点只能是黑色结点。 4.每个结点到其所有叶子结点的路径的黑色结点个数相同。 5.指向空的…...
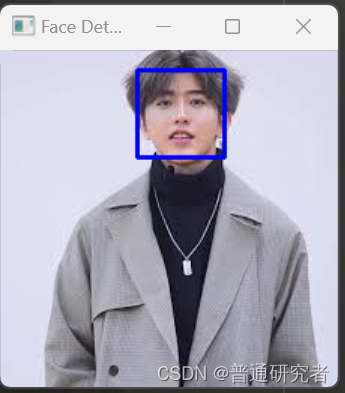
opencv-使用 Haar 分类器进行面部检测
Haar 分类器是一种用于对象检测的方法,最常见的应用之一是面部检测。Haar 分类器基于Haar-like 特征,这些特征可以通过计算图像中的积分图来高效地计算。 在OpenCV中,Haar 分类器被广泛用于面部检测。以下是一个简单的使用OpenCV进行面部检测…...

C++纯虚函数和抽象类 制作饮品案例(涉及知识点:继承,多态,实例化继承抽象类的子类,多文件实现项目)
一.纯虚函数的由来 在多态中,通常父类中虚函数的实现是毫无意义的,主要都是调用子类重写的内容。例如: #include<iostream>using namespace std;class AbstractCalculator { public:int m_Num1;int m_Num2;virtual int getResult(){r…...

什么是网关和链路追踪,以及怎么使用?
在云计算中,网关和链路追踪也是非常重要的。云服务提供商通常会提供网关和链路追踪等相关服务来帮助用户管理和优化云计算网络。 云计算中的网关通常包括以下几种: 虚拟网络网关:用于将云中不同虚拟网络之间相互连接,实现云内不同…...

git 文件被莫名其妙的或略且无论如何都查不到哪个.gitignore文件忽略的
先说解决办法:git check-ignore -v [文件路径] 这个命令会返回一个忽略规则,以及该规则在哪个文件中定义的,该规则使得指定的文件被忽略。 1.遇到的问题 同项目组,其他同学都可以正常的提交.meta文件,我的提交就出现以…...
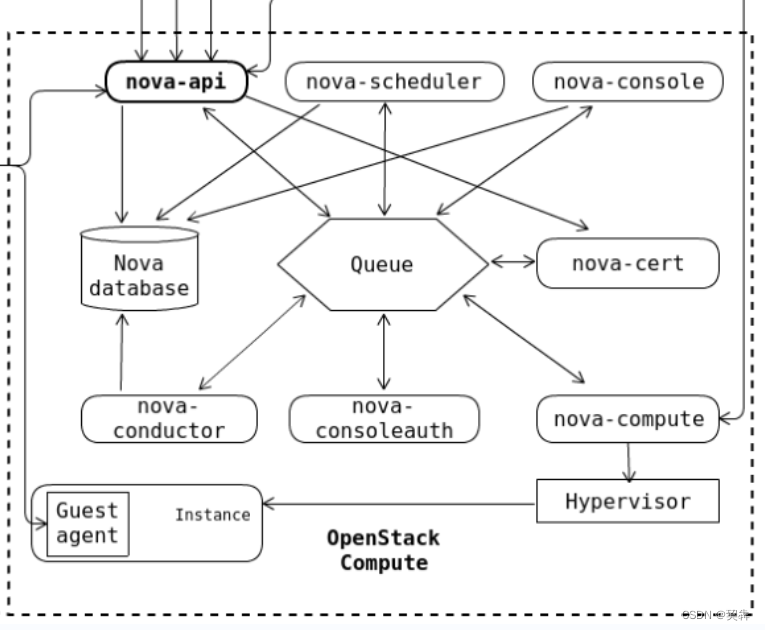
nova组件简介
目录 组件关系图 controller节点 openstack-nova-api.service: openstack-nova-conductor.service: openstack-nova-consoleauth.service: openstack-nova-novncproxy.service: openstack-nova-scheduler.service: openstack-nova-conductor.service详解 作用和功能&…...

【Vue】响应式与数据劫持
Vue.js 是一个渐进式的 JavaScript 框架,其中最重要的一个特性就是响应式(Reactivity)。Vue 借助数据劫持(Data Observation)技术实现了对数据的响应式更新,当数据发生变化时,它会自动重新渲染视…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
