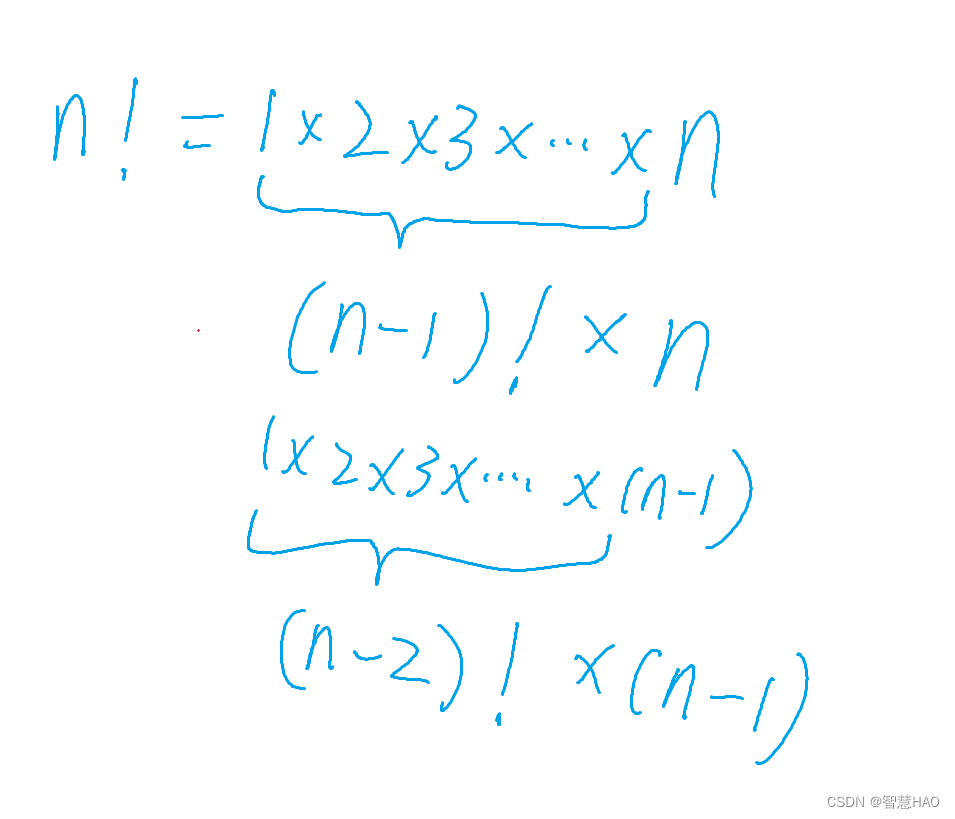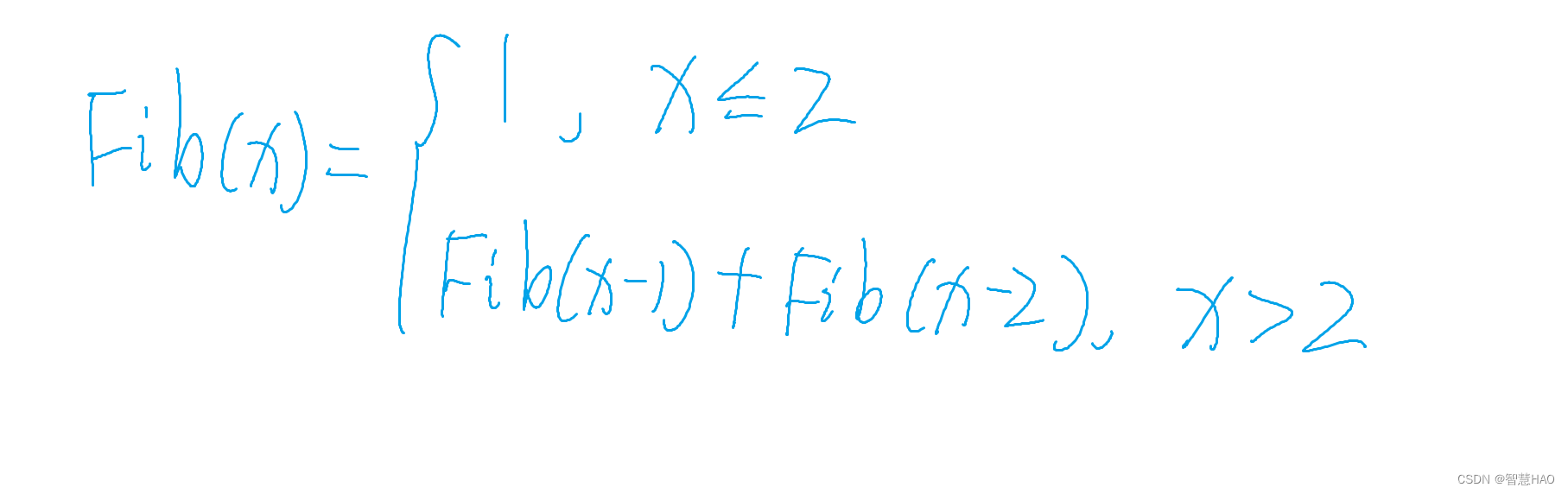【C语言】函数(四):函数递归与迭代,二者有什么区别
目录
- 前言
- 递归
- 定义
- 递归的两个必要条件
- 接受一个整型值(无符号),按照顺序打印它的每一位
- 使用函数不允许创建临时变量,求字符串“abcd”的长度
- 求n的阶乘
- 求第n个斐波那契数
- 迭代
- 总结
- 递归与迭代的主要区别
- 用法不同
- 结构不同
- 时间开销不同
- 两个经典问题
前言
从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事!故事是什么?“从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事!故事是什么?‘从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事!故事是什么?……’”
递归
定义
计算机科学中,递归是是指在函数的定义中使用函数自身的方法。它通常把一个大型的复杂问题层层转化为一个与原问题相似的规模较小的问题来求解,递归只需要少量的代码就可以描述出解题过程中的多次重复计算,大大减少了程序的代码量。
递归的主要思想是:大化小
递归的两个必要条件
1.存在限制条件,当满足这个限制条件时,递归停止。
2.每次递归调用之后越来越接近限制条件。
错误示例:
#include<stdio.h>int main()
{printf("hello world!\n");main();return 0;
}
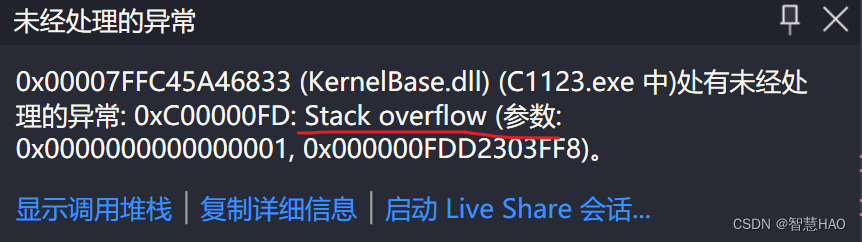
画红线的地方,意思是栈溢出,从上面写的程序中发现,递归没有停止的限制条件,导致死递归。
接受一个整型值(无符号),按照顺序打印它的每一位
示例1:
问题描述:
接受一个整型值(无符号),按照顺序打印它的每一位。
样例输入:1234
样例输出:1 2 3 4
代码示范:
#include<stdio.h>void Func(unsigned int x)
{if (x > 9){Func(x / 10);}printf("%d ", x % 10);
}
int main()
{unsigned int num = 0;scanf("%d", &num); //假设输入的是123Func(num);return 0;
}
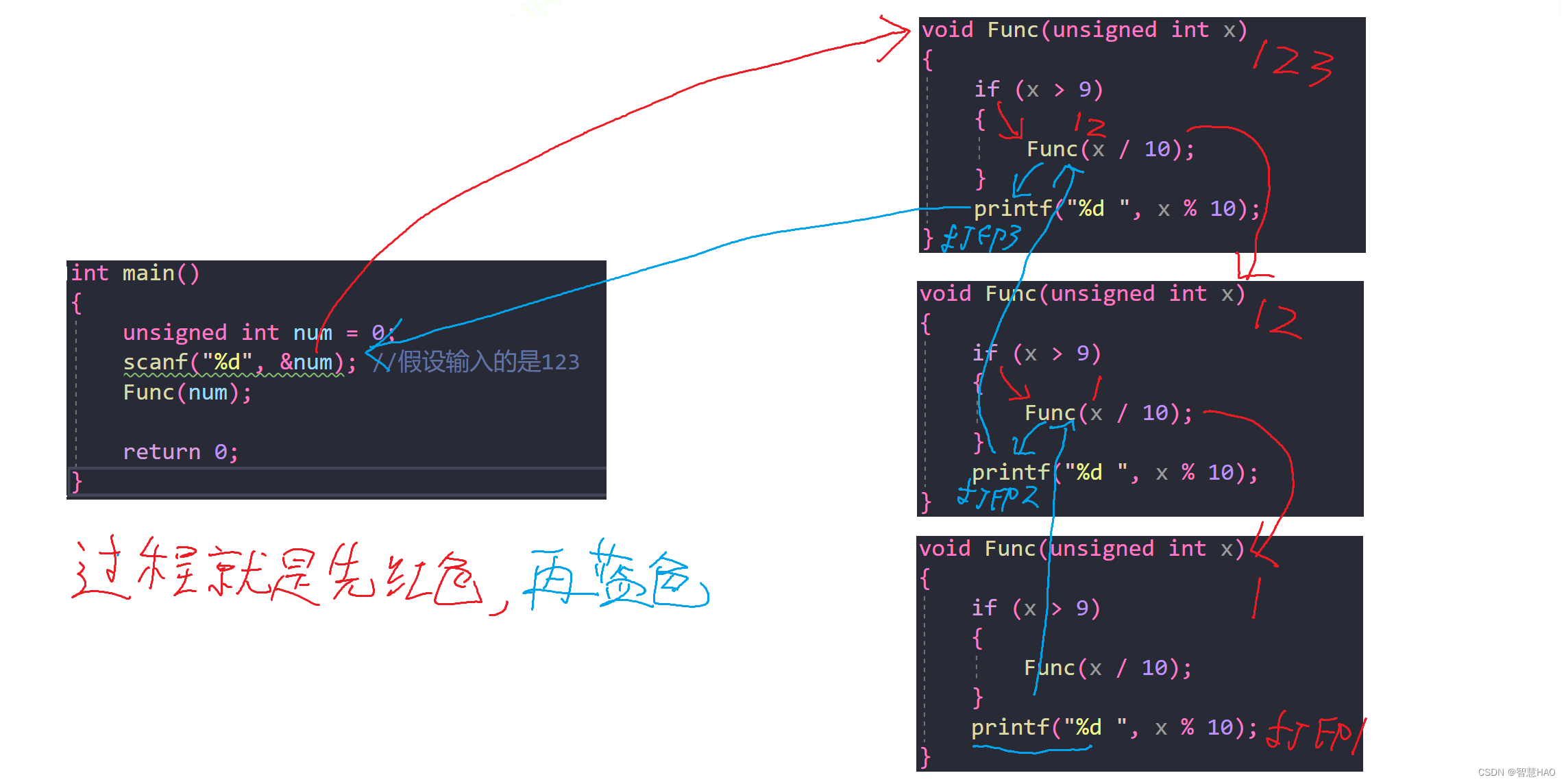
到这里对递归应该有一个比较清晰的认识了,在图中红色过程表示的就是递归当中的“递”,蓝色过程表示的就是递归当中的“归”。
使用函数不允许创建临时变量,求字符串“abcd”的长度
示例2:
问题描述:
使用函数不允许创建临时变量,求字符串“abcd”的长度
分析: 直接求字符串“abcd”的长度,它是字符串,在前面文章中说过字符串的结束标志是 \0
代码展示:
#include<stdio.h>
#include<string.h>int Length(char* l)
{int count = 0;while (*l != '\0'){count++;l++;}return count;
}
int main()
{char arr[] = "abcd";int len = Length(arr);printf("%d\n", len);return 0;
}
这段代码完全没有问题,但是题目要求不允许创建临时变量,这里创建了临时变量count。
再分析:
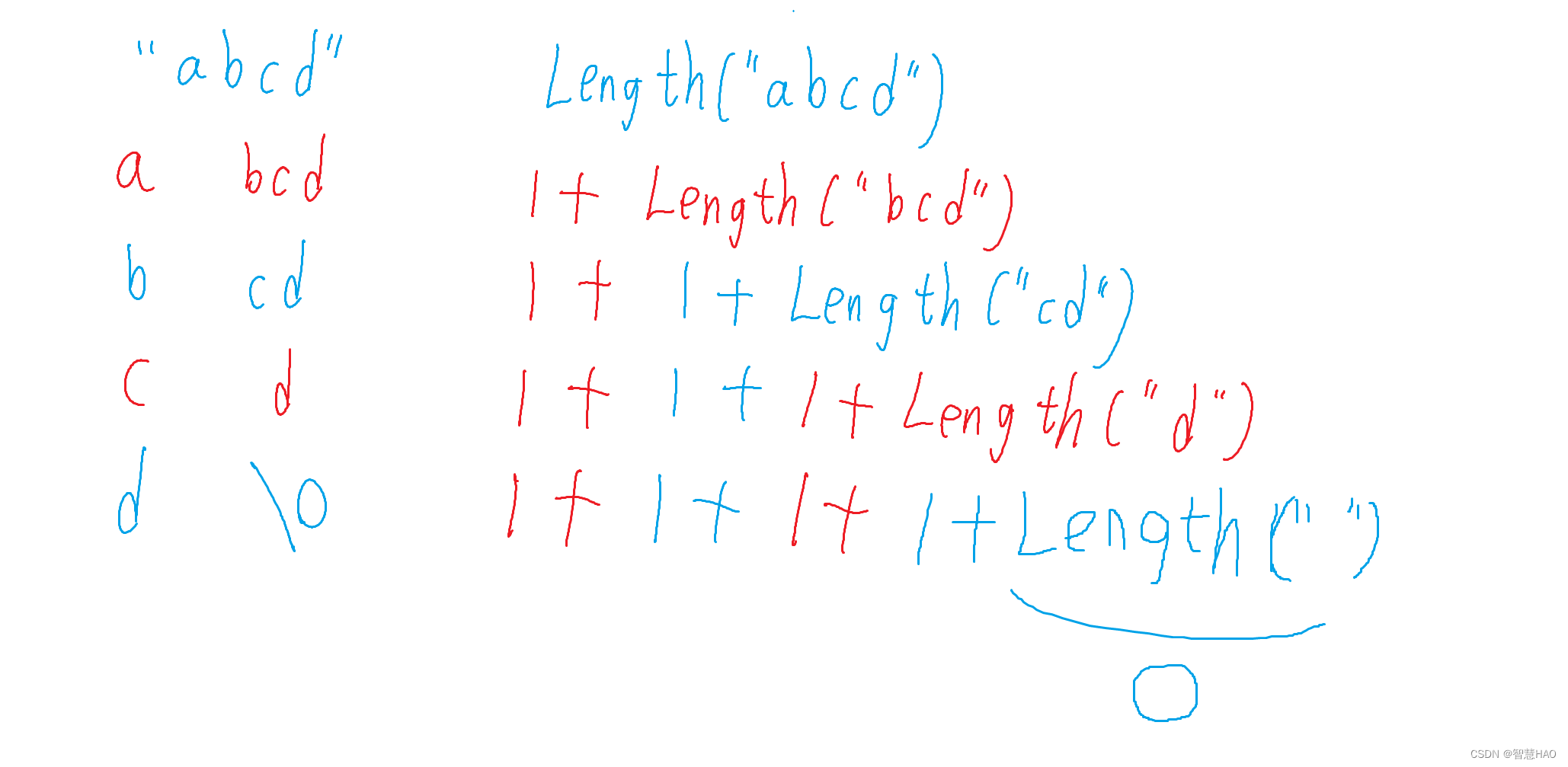
所以我们可以将Length函数写成递归的形式:
//递归
int Length(char* length)
{if (*length == '\0')return 0;elsereturn 1 + Length(length + 1);
}
我们再分析过程:

求n的阶乘
我们回顾一下n!怎么算:
#include<stdio.h>int Func(int x)
{int i = 0;int j = 1;for (i = 1; i <= x; i++){j *= i;}return j;
}
int main()
{int n = 0;scanf("%d", &n);int result = Func(n);printf("%d\n", result);return 0;
}
上述代码是非递归的形式,我们再来思考一下如何使用递归来写n!:
我们可以发现n!=n*(n-1)!
所以Func函数可以写成:
int Func(int x)
{if (x <= 1)return 1;else return x * Func(x - 1);
}
求第n个斐波那契数
斐波那契数列由0和1开始,之后的斐波那契数就是由之前的两数相加而得出。
前几个斐波那契数是:
1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144……
也就是说从第三个数开始,后面的每一个斐波那契数都是前两个数的和。
到这里就可以直接写代码了:
#include<stdio.h>int Fib(int n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);int result = Fib(n);printf("%d\n", result);return 0;
}
这时候我们信心满满,让计算机帮我求第50个斐波那契数,当我们执行程序后在键盘输入50,却发现,等了很久都没有发现它输出内容。
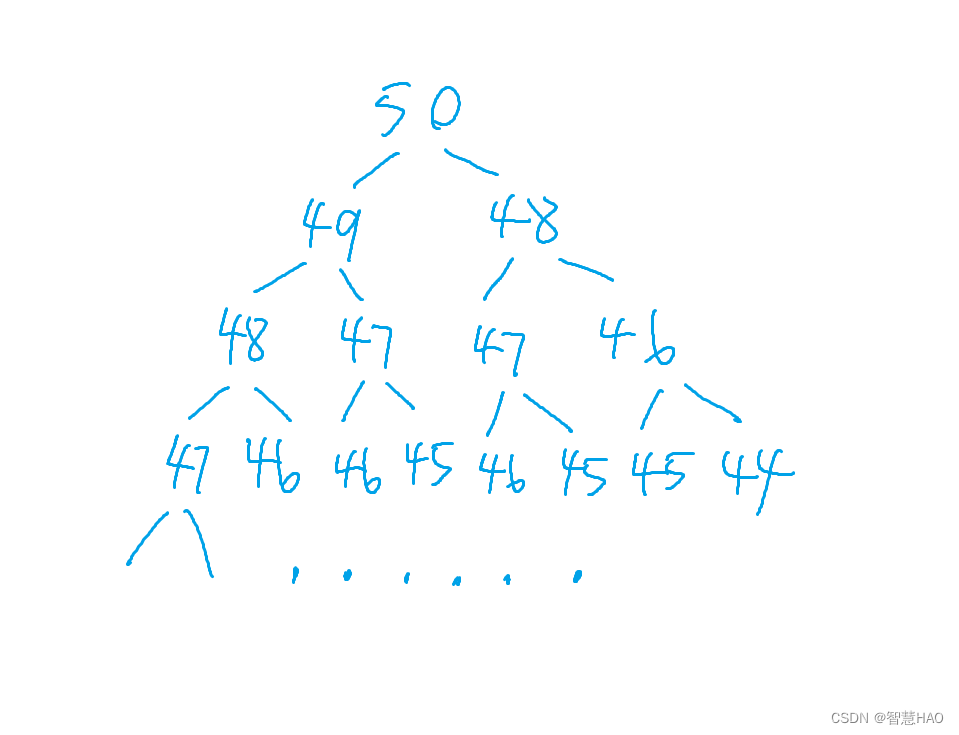
为什么?
我们要求第50个斐波那契数,就需要计算第49个和第48个数,计算第49个数又需要计算第48个数和第47个数,可以想一下上面这个图画到末端需要画多少,除了前两个数,要算2的48次方,而int型只占4个字节的内存,也就是32位,2的32次方都已经42亿多,可想而知计算量非常庞大。按照递归的方式要进行大量的重复计算。我们可以做一个计数,计算第40个斐波那契数中3被计算了多少次,你会发现3被计算了将近四千万次,效率非常低。所以不是因为计算机偷懒没算,它也在拼命地计算,只是量太大,它一会儿也算不出来。
那么应该如何改进呢?
迭代
在计算机科学中,迭代是程序中对一组指令(或一定步骤)的重复。它既可以被用作通用的术语(与“重复”同义),也可以用来描述一种特定形式的具有可变状态的重复。可以简单理解为普通循环。但与普通循环有所差别,迭代时,循环代码中参与运算的变量同时是保存结果的变量,当前保存的结果作为下一次循环计算的初始值
我们知道函数形参是被存放在栈区当中,递归每“递”一次,就要开辟一个变量的内存,那么当参数非常大的时候,栈区内存不够了,栈区放不下了,也就是说栈区空间已经被耗尽了,但是你的东西还没放完,这个时候就会出现栈溢出的现象。
那么我们回头再看求第n个斐波那契数,能否将递归转换成迭代的形式。
while (n >= 3){c = a + b;a = b;b = c;n--;}return c;
那么当n小于3的时候,也就是第1个或者第2个数,都是1,所以在给a,b,c初始化的时候,都赋值为1即可。
完整代码:
#include<stdio.h>
//迭代
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n >= 3){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0;scanf("%d", &n);int result = Fib(n);printf("%d\n", result);return 0;
}
这个时候程序运行后输入50,尽管结果仍然是错误的,但是速度非常快。解决了大量重复计算的问题。
总结
当使用递归可能会导致栈溢出时,程序效率明显下降的时候,就不能够使用递归了。
如何解决?
1.可以使用迭代替换递归。
2.在递归函数设计中可以使用static限制变量,让变量申请一块内存后,在那一块内存折腾。不仅不再大量开辟栈区内存,从而导致栈溢出,并且static可以保存递归时的中间状态,并且为各个调用层所访问。
- 递归代码量少,迭代不易想到,递归比迭代更清晰。所以许多问题采用递归的方式解释。
- 迭代实现比递归实现的代码可读性差,但是效率高。
- 当问题复杂的时候,难以用迭代实现,此时使用递归会更加简洁。
递归与迭代的主要区别
用法不同
- 迭代是代码块的重复。虽然需要更多的代码,但时间复杂度通常小于递归的时间复杂度。
- 递归是多次调用自身,因此代码长度非常小。但是,当有非常非常多次的递归调用时,递归的时间复杂度可能会呈指数级增长。
结构不同
- 迭代是环结构,从初始状态开始,每次迭代都遍历这个环,并更新状态,多次迭代直到到达结束状态。
- 递归是树结构,从字面可以理解为重复“递”和“归”的过程,当“递”到达底部时就会开始“归”。
时间开销不同
- 与迭代相比,递归具有大量的开销。递归具有重复函数调用的开销,即由于重复调用同一函数,代码的时间复杂度增加了许多倍。
两个经典问题
- 汉诺塔问题
- 青蛙跳台阶问题
相关文章:

【C语言】函数(四):函数递归与迭代,二者有什么区别
目录 前言递归定义递归的两个必要条件接受一个整型值(无符号),按照顺序打印它的每一位使用函数不允许创建临时变量,求字符串“abcd”的长度求n的阶乘求第n个斐波那契数 迭代总结递归与迭代的主要区别用法不同结构不同时间开销不同…...

[原创](免改BIOS)使用Clover升级旧电脑-(高阶玩法)让固态硬盘内置Win11 PE启动系统
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XXQQ: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、Delphi…...

React项目中发生空白但不报错的原因分析和解决?
文章目录 前言组件渲染问题状态管理问题异步操作问题代码错误但未抛出异常如果我们使用的是chorme浏览器的话,可以下载一个开发者工具,例如下图:代码审查使用调试工具日志和输出检查外部依赖异步操作终极大法,不到万不得已不可以使…...

redis运维(十七)事务
一 redis事务 事务核心参考 ① 基础概念 1、场景引入核心:通过现象思考原因? 2、事务的概念 3、事务四大特性说明: redis只具备部分特性 重点1: 原子性和一致性 重点2: 隔离性和持久性 ② redis的事务 1、基础铺垫备注&…...

Vue框架学习笔记——Vue实例中el和data的两种写法
文章目录 前文提要Vue实例的el第一种写法第二种写法小结 Vue实例中data第一种写法,对象式效果图片第二种写法,函数式效果图片小结 前文提要 本文仅做自己的学习记录,如有错误,请多谅解 Vue实例的el 第一种写法 <body><…...

libbz2 for Mac OS makefile
git地址:git://sourceware.org/git/bzip2.git a文件Makefile # ------------------------------------------------------------------ # This file is part of bzip2/libbzip2, a program and library for # lossless, block-sorting data compression. # # bzip…...
测试工具JMeter的使用
目录 JMeter的安装配置 测试的性能指标 TPS 响应时长 并发连接 和 并发用户 CPU/内存/磁盘/网络 负载 性能测试实战流程 JMeter JMeter快速上手 GUI模式 运行 HTTP请求默认值 录制网站流量 模拟间隔时间 Cookie管理器 消息数据关联 变量 后置处理器 CSV 数据文…...

C++编程——输入
#include<bits/stdc.h> using namespace std; int main(){//beginint a 0, b 0, c 0, d 0, e 0;char f1, f2;char g[30];scanf("%d", &a); //输入整数并赋值给变量ascanf("%d", &b); //输入整数并赋值给变量bscanf("%d", &…...
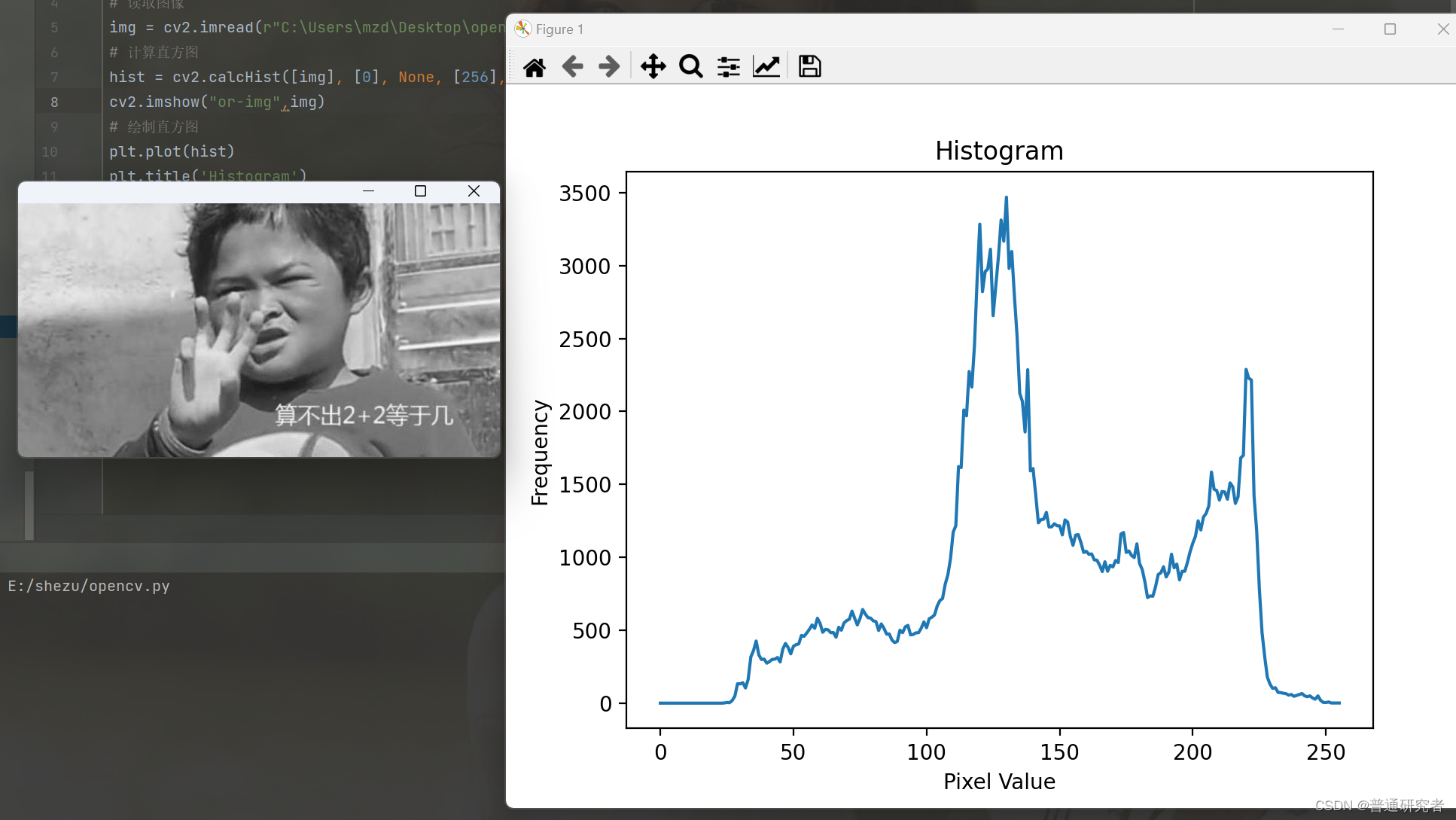
opencv-直方图
直方图是一种对图像亮度分布的统计表示,它显示了图像中每个灰度级别的像素数量。在OpenCV中,你可以使用cv2.calcHist() 函数计算直方图。 以下是一个简单的示例,演示如何计算和绘制图像的直方图: import cv2 import numpy as np …...
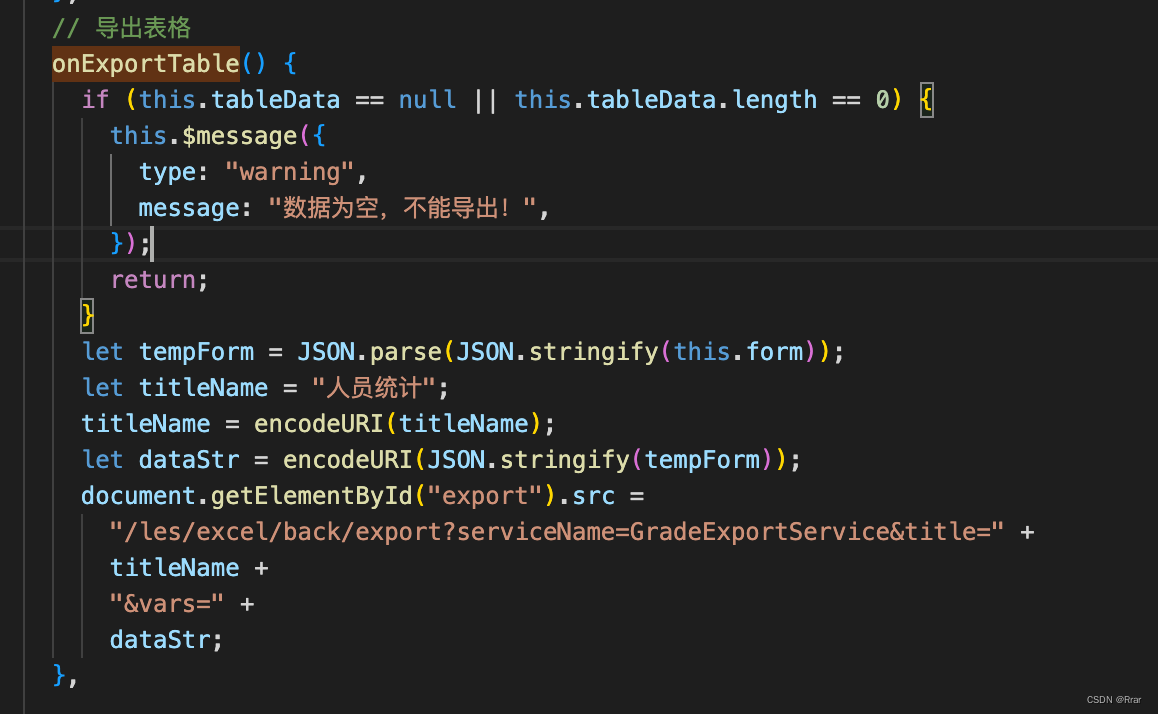
el-table表格排序(需要后端判别),el-table导出功能(向后端发送请求)
(1)表格排序 (2)简单的table导出功能(需要后台支撑)必须要有iframe (3)页面所有代码: <template><div class"mainContainer"><el-form:model&…...
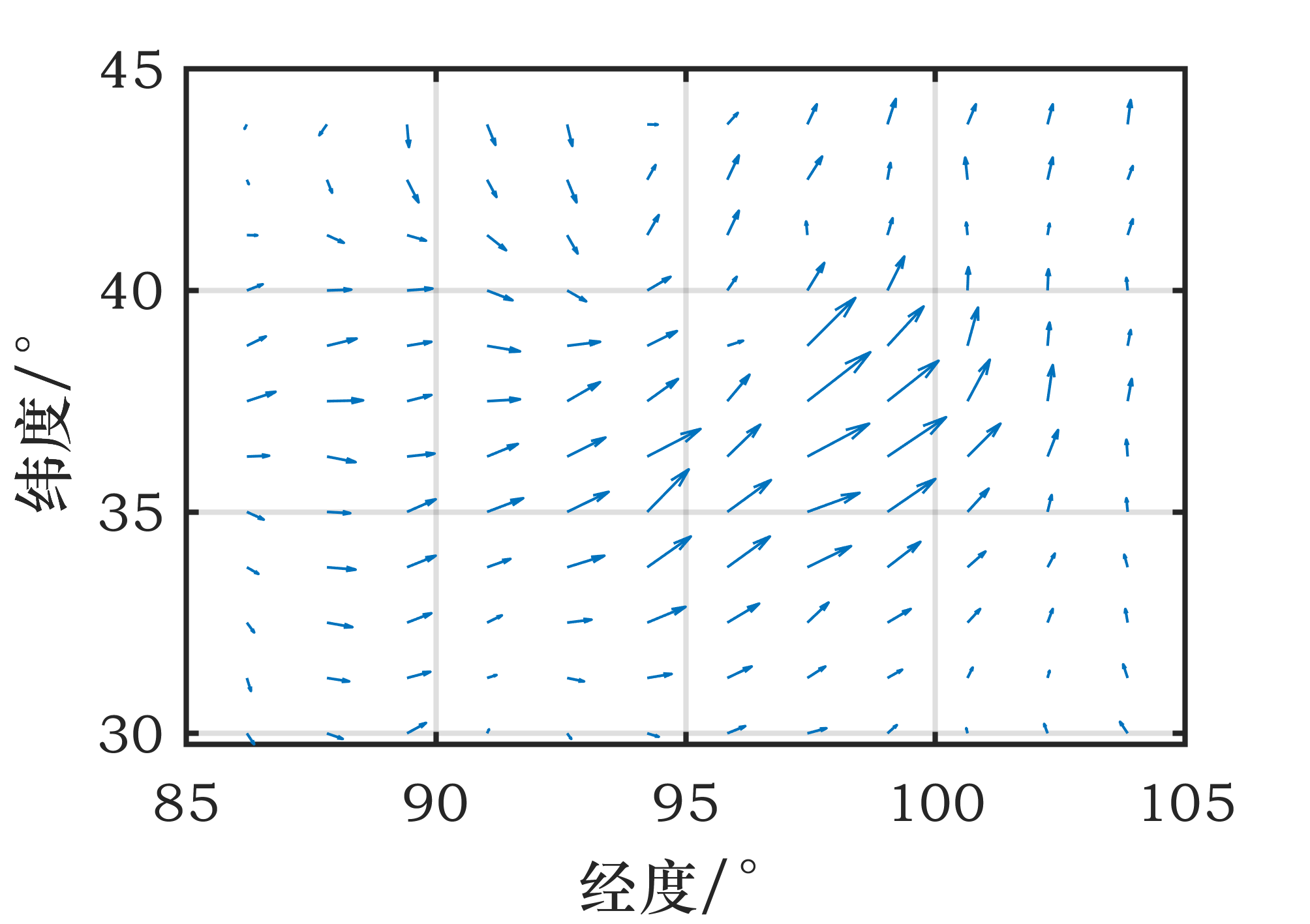
【MATLAB】全网入门快、免费获取、持续更新的科研绘图教程系列2
14 【MATLAB】科研绘图第十四期表示散点分布的双柱状双Y轴统计图 %% 表示散点分布的双柱状双Y轴统计图%% Made by Lwcah (公众号:Lwcah) %% 公众号:Lwcah %% 知乎、B站、小红书、抖音同名账号:Lwcah,感谢关注~ %% 更多…...

git与ssh多账户共存
git与ssh多账户共存 前言git多账户ssh多公钥参考 前言 在使用git与ssh时,经常会遇到多个账户共存的情况 例如使用不同的公钥登陆到不同的服务;使用不同的git信息进行commit git多账户 在默认情况下 git的信息存在 ~/.gitconfig 可以使用命令查看 git…...
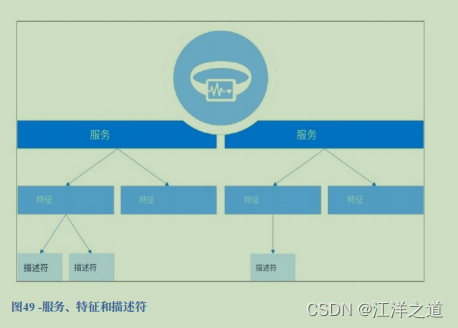
BLE协议栈入门学习
蓝牙LE栈 物理层 频带 蓝牙LE在2400MHz到2483.5MHz范围内的2.4GHz免授权频段工作,该频段分为40个信道,每个信道间隔为2MHz。 时分 蓝牙LE是半双工的,可以发送和接收,但不能同时发送和接收,然而,所有的设…...

【反射】简述反射的构造方法,成员变量成员方法
🎊专栏【JavaSE】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 🥰欢迎并且感谢大家指出我的问题 文章目录 🎄什么是反射🎄获取class对象的三种方式⭐代码实现 dz…...

acwing算法基础之数学知识--求卡特兰数
目录 1 基础知识2 模板3 工程化 1 基础知识 题目:给定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,求它们能排成的所有序列中,能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个? 输出的答案对 1 0 …...
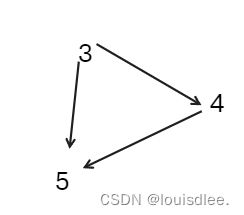
《洛谷深入浅出基础篇》P4017最大食物链————拓扑排序
上链接:P4017 最大食物链计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P4017 上题干: 题目背景 你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了,因为她总是…...
设置定时自动请求测试_自动定时循环发送http_post请求---postman工作笔记001
其实就是创建接口文件夹的时候,有个monitor collection 用来监听接口执行情况,这里就可以设置 可以看到多久执行一次对吧,这里可以设置每几分钟执行一次,一共执行多少次等等 但是这里要说明一下,如果需要使用monitor功能,必须需要登录, 所以如果这里点击monitor collection…...

Vue3封装全局插件
定义一个全局加载组件 一、首先定义dom元素 定义一个index.vue文件 <template><div class"loading">loading...</div> </template> <script setup lang"ts"></script> <style scoped> .loading {display: fl…...

【Python 训练营】N_6 求素数
题目 判断101-200之间有多少个素数,并输出所有素数。 分析 判断素数的方法:用一个数分别去除2到sqrt(这个数),如果能被整除,则表明此数不是素数,反之是素数。 答案 h 0 leap 1 from math import sqrt from sys …...
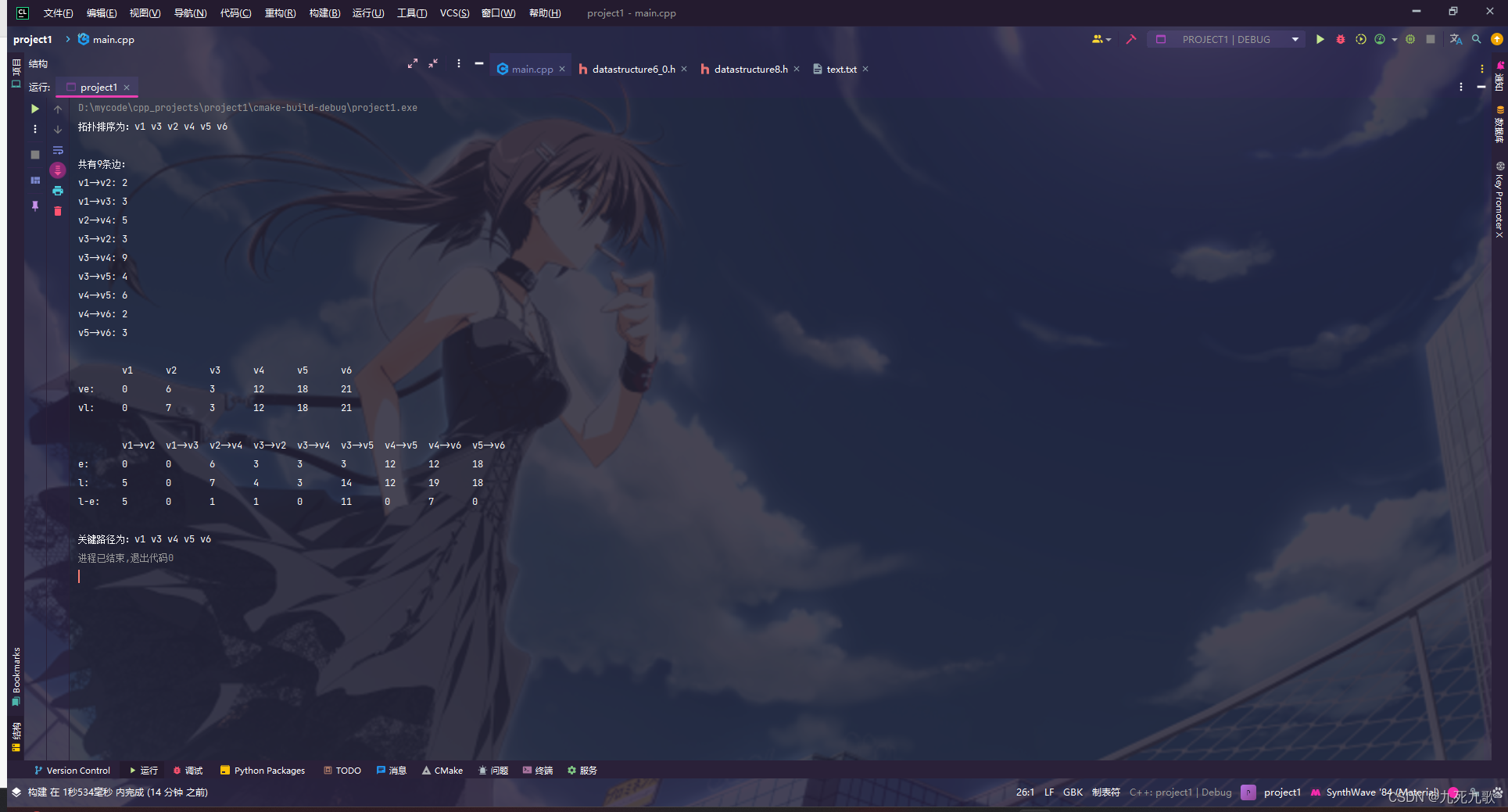
【图论】关键路径求法c++
代码结构如下图: 其中topologicalSort(float**, int, int*, bool*, int, int)用来递归求解拓扑排序,topologicalSort(float**, int*&, int, int, int)传参图的邻接矩阵mat与结点个数n,与一个引用变量数组topo,返回一个布尔值…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...