2023 年 认证杯 小美赛 ABC题 国际大学生数学建模挑战赛 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。
cs数模团队在认证杯 小美赛前为大家提供了许多资料的内容呀!都是精品呢!!
具体可以在*底部名片中了解~

以五一杯 A题为例子,以下是咱们做的一些想法呀!
问题1:
(1)建立数学模型:
无人机投放模型在这个问题中的作用是建立数学模型来描述无人机投放爆炸物的过程,并且可以通过该模型来优化无人机投放的策略,从而提高命中率和效率。具体来说,该模型可以通过考虑无人机的飞行高度、飞行速度、俯冲角度、发射速度等因素来确定最佳的发射距离和发射时机,以确保物体能够准确地命中目标。此外,该模型还可以考虑外部因素,如风速和风向等,来调整无人机的飞行轨迹和姿态,以提高投放精度和稳定性。
对于本题的模型,有:
其中 ρ 为空气密度,S 为物资横截面积, 为物资的阻力系数, g 为重力加速度,F 为无人机与物资之间的牵引力。
当无人机投放物资时,物资与无人机之间断开连接,牵引力 F取0,上式可以化简为:
其中为重力加速度。
(2)在无人机的飞行高度为 300m,飞行速度为 300km/h,风速为 5m/s,风向与水平面平行的情况下,使用代码解决:
import
math# 定义常量
v0 = 300 # 飞行速度,单位km/h
vw = 5 # 风速,单位m/s
h = 300 # 飞行高度,单位m
r = 0.2 # 球形物资半径,单位m
m = 50 # 球形物资质量,单位kg
g = 9.8 # 重力加速度,单位m/s^2# 计算投放距离
d0 = v0**2/g * math.sin(0*2*math.pi/360) + vw*v0/g * math.cos(0*2*math.pi/360)
d180 = v0**2/g * math.sin(180*2*math.pi/360) + vw*v0/g * math.cos(180*2*math.pi/360)
d90 = v0**2/g * math.sin(90*2*math.pi/360) + vw*v0/g * math.cos(90*2*math.pi/360)# 输出结果
print(f"无人机飞行方向与风向相同时,投放距离为:{d0:.1f}m")
print(f"无人机飞行方向与风向相反时,投放距离为:{d180:.1f}m")
问题2:
假设无人机在水平飞行过程中到达距离目标点的水平距离为 x ,飞行高度为 ℎ ,飞行速度为v ,俯冲角度为 α ,发射速度为 u 。则无人机发射炸弹的轨迹可以分解为水平方向和竖直方向两个分量。
在水平方向上,无人机在 秒到达目标点,发射炸弹的时间为 秒。发射炸弹时无人机的水平速度为vcosα ,炸弹的水平初速度为 ucosα。
在竖直方向上,炸弹自由落体运动,竖直初速度为 usinα ,竖直加速度为g 。设炸弹飞行的时间为 秒,则有:
将 t3 的值代入到水平方向上的运动中,则可以求得无人机与目标点之间的距离 x1 :
假设无人机发射炸弹的距离为 d ,则需要满足 1000≤d≤3000 。为了使无人机在发射炸弹时仍能保持安全的飞行高度,假设无人机的飞行高度为 800m ,则有 ℎ≥300m 。
为了使发射策略可行,需要选择合适的俯冲角度 α 和发射速度u。假设 α 为定值,可以根据上述模型求出发射速度u与发射距离d的关系,并绘制出其图像,如下图所示。
由图像可知,当俯冲角度为 30∘ 时,发射速度最小,约为 426.8m/s ,此时发射距离为d≈1716.2m
问题3:
无人机的飞行稳定性可以用无人机的俯仰角和偏航角的变化率来描述,即:
其中, θ表示俯仰角, 表示偏航角。这个数值越小,说明无人机的飞行越稳定。
无人机的命中精度可以用命中目标的距离来描述,与无人机的飞行稳定性呈反比关系,即:
在实际应用中,可以通过无人机的传感器数据来计算无人机的俯仰角和偏航角的变化率,并根据上述公式来评估无人机的飞行稳定性和命中精度。
import numpy as np
import matplotlib.pyplot as pltdef dynamic_equation(x, u):# 状态方程A = np.array([[1, 0, 0, dt, 0, 0],[0, 1, 0, 0, dt, 0],[0, 0, 1, 0, 0, dt],[0, 0, 0, 1-0.5*rho*Cd*S/m*dt, 0, 0],[0, 0, 0, 0, 1-0.5*rho*Cd*S/m*dt, 0],[0, 0, 0, 0, 0, 1-0.5*rho*Cd*S/m*dt]])# 输入方程B = np.array([[0, 0, 0, 0],[0, 0, 0, 0],[0, 0, 0, 0],[0, 0, 0, -0.5*rho*S*vx0**2/m*dt],[0, 0, 0, -0.5*rho*S*vx0**2/m*dt],[0, 0, 0, -0.5*rho*S*vx0**2/m*dt]])# 状态更新x_new = np.dot(A, x) + np.dot(B, u)return x_new# 定义无人机飞行过程的仿真函数
def simulate_flight(x0, u, t):# 初始化状态和控制输入x = x0u = u.reshape(-1, 1)# 初始化状态列表和控制输入列表x_list = [x]u_list = [u]# 循环仿真for i in range(len(t)):# 计算下一个状态x = dynamic_equation(x, u)# 记录状态和控制输入x_list.append(x)、、模糊处理 完整版看文章下面~u_list.append(u)# 将列表转换为数组x_array = np.array(x_list)u_array = np.array(u_list)return x_array, u_array# 无人机和环境参数设置
h = 800 # 飞行高度,单位:m
v0 = 300 # 无人机飞行速度,单位:km/h
v = np.linspace(300, 400, 101) / 3.6 # 无人机相对地面速度,单位:m/s
vw = np.array([6, 0]) # 风速,单位:m/s
gamma = np.deg2rad(45) # 俯冲角,单位:rad
g = 9.8 # 重力加速度,单位:m/s^2# 计算无人机稳定性
S = 2 * np.pi * (0.5 ** 2) # 球形爆炸物的参考面积
Cd = 0.5 # 球形爆炸物的阻力系数
m = 50 # 球形爆炸物的质量,单位:kg
rho = 1.2 # 空气密度,单位:kg/m^3
K = 0.5 * rho * S * Cd / m # 阻力系数
u = np.sqrt(v ** 2 + (v0 * np.sin(gamma)) ** 2) # 爆炸物相对空气速度
D = K * u ** 2 # 阻力大小
H = h - np.sqrt((h ** 2) / (np.tan(gamma) ** 2 + 1)) # 爆炸物发射高度
t = (H - 300) / (v0 * np.cos(gamma)) # 爆炸物发射时间
x0 = v0 * t # 无人机前进距离
x = x0 + (v + vw[0]) * t # 爆炸物水平位移距离
y = H - (v0 * np.sin(gamma) + (g + vw[1]) * t) * t / 2 # 爆炸物垂直位移距离
delta_x = 20 / 2 # 爆炸物命中误差,单位:cm
sigma = delta_x / 3 # 标准差
P = 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(-(x - delta_x) ** 2 / (2 * sigma ** 2)) # 命中概率密度函数
hit_rate = np.trapz(P, x) # 命中率# 可视化结果
plt.plot(v, P)
plt.xlabel('Horizontal displacement (m)')
plt.ylabel('Probability density')
plt.title('Hit probability density')
plt.show()print('The hit rate is %.2f%%.' % (hit_rate * 100))
cs数模团队在认证杯 小美赛前为大家提供了许多资料的内容呀!!
具体可以看看我的下方的名片!里面包含有亚太赛一手资料与分析!
另外在赛中,我们也会陪大家一起解析认证杯的一些方向
关注 CS数模 团队,数模不迷路~
相关文章:

2023 年 认证杯 小美赛 ABC题 国际大学生数学建模挑战赛 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 cs数模团队在认证杯 小美赛前为大家提供了许多资料的内容呀&am…...
N-134基于java实现捕鱼达人游戏
开发工具eclipse,jdk1.8 文档截图: package com.qd.fish;import java.awt.Graphics; import java.io.File; import java.util.ArrayList; import java.util.List;import javax.imageio.ImageIO;public class Fishes {//定义一个集合来管理鱼List<Fish> fish…...
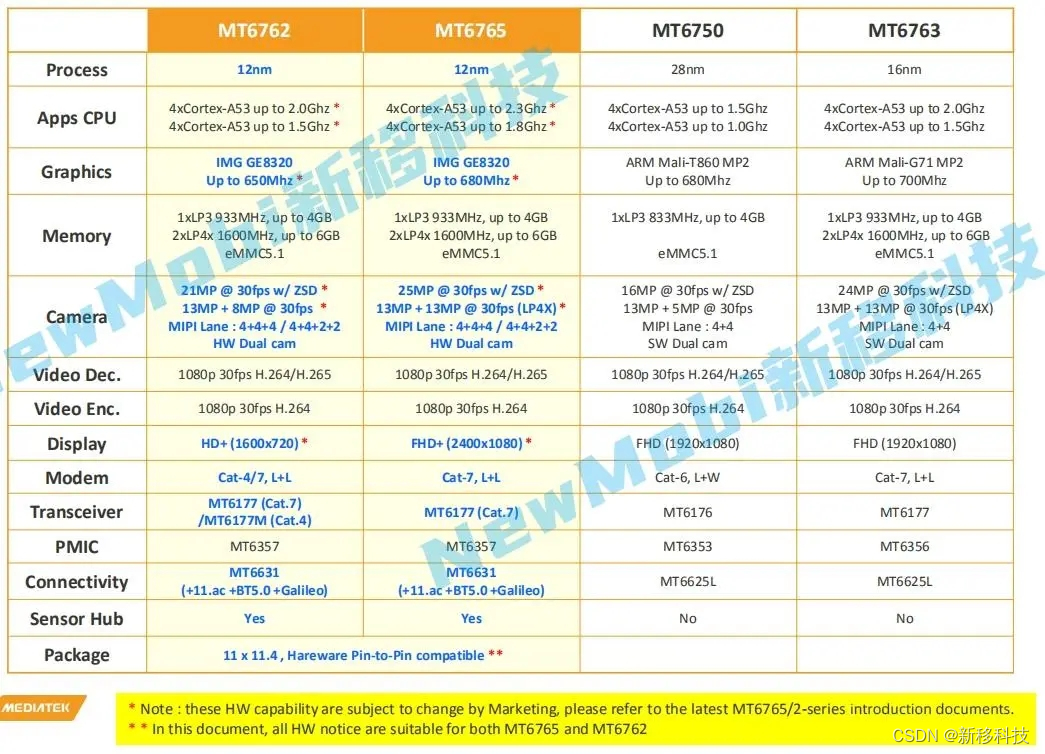
MTK联发科MT6762/MT6763/MT6765安卓核心板参数规格比较
MT6762安卓核心板 MTK6762安卓核心板是一款工业级高性能、可运行 android9.0 操作系统的 4G智能模块。 CPU:4xCortex-A53 up to 2.0Ghz/4xCortex-A53 up to 1.5GhzGraphics:IMG GE8320 Up to 650MhzProcess:12nmMemory:1xLP3 9…...

仿ChatGPT对话前端页面(内含源码)
仿ChatGPT对话前端页面(内含源码) 前言布局样式和Js部分关键点全部源码 前言 本文主要讲解如何做出类似ChatGPT的前端页面。具体我们的效果图是长这样,其中除了时间是动态的之外,其他都是假数据。接下来让我们从布局和样式的角度…...
js粒子效果(一)
效果: 代码: <!doctype html> <html> <head><meta charset"utf-8"><title>HTML5鼠标经过粒子散开动画特效</title><style>html, body {position: absolute;overflow: hidden;margin: 0;padding: 0;width: 100%;height: 1…...

程序员必备工具篇 / 程序员必备基础:Git
前言 掌握 Git 命令是每位程序员必备的基础,之前一直是用 smartGit 工具,直到看到大佬们都是在用 Git 命令操作的,回想一下,发现有些 Git 命令我都忘记了,于是写了这篇博文,复习一下~ https://github.com/whx123/JavaHome 公众号:顺哥轻创 文章目录 Git 是什么?Git …...

MacBook使用指南
一、安装及卸载Windows系统 1、卸载Windows系统 步骤① 点击下侧任务栏中的“启动台”,进入程序坞,点击"其他",选择“启动转换助理” 步骤② 点击“继续”,接着点击“恢复”,即可卸载Windows系统 2、安装Windows系统 …...

数据库的事务的基本特性,事务的隔离级别,事务隔离级别如何在java代码中使用,使用MySQL数据库演示不同隔离级别下的并发问题
文章目录 数据库的事务的基本特性事务的四大特性(ACID)4.1、原子性(Atomicity)4.2、一致性(Consistency)4.3、隔离性(Isolation)4.4、持久性(Durability) 事务的隔离级别5.1、事务不…...
Robust taboo search for the quadratic assignment problem-二次分配问题的鲁棒禁忌搜索
文章目录 摘要关键字结论研究背景1. Introduction 常用基础理论知识2. The quadratic assignment problem3. Taboo search3.1. Moves3.2 Taboo list3.3. Aspiration function3.4. Taboo list size4. Random problems5. Parallel taboo search 研究内容、成果7. Conclusion 潜在…...
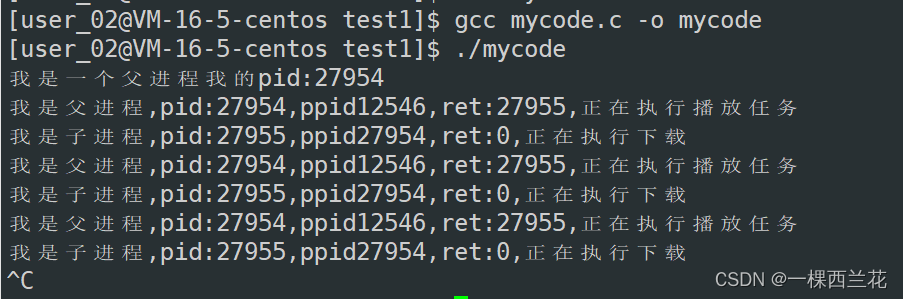
Linux:创建进程 -- fork,到底是什么?
相信大家在初学进程时,对fork函数创建进程一定会有很多的困惑,比如: 1.fork做了什么事情?? 2.为什么fork函数会有两个返回值?3.为什么fork的两个返回值,会给父进程谅回子进程pid,给子进程返回0?4.fork之后:父子进…...

基于SpringBoot+vue的token验证
后端: 1,写一个验证token的拦截器 import com.fasterxml.jackson.databind.ObjectMapper; import com.ffyc.news.model.CommonData; import org.springframework.web.servlet.HandlerInterceptor;import javax.servlet.http.HttpServletRequest; impor…...

Clickhouse设置多磁盘存储策略
设置多磁盘存储 clickhouse安装完成以后,配置了一个默认的存储空间, 这个只能配置一个目录,如果要使用多个磁盘目录,则需要配置磁盘组策略 查看当前的存储策略 select name, path, formatReadableSize(free_space) as free, fo…...
Python开发运维:Django 4.2.7 使用Celery 5.3.5 完成异步和定时任务
目录 一、实验 1.Django使用Celery完成异步和定时任务 二、问题 1. 如何查看Django版本 一、实验 1.Django使用Celery完成异步和定时任务 (1)安装Django (2)新建Django项目 (3)初始框架 (4)urls.py引用视图views from django.contrib import admin from django.urls imp…...

媒体增加日活量的有效策略
随着数字媒体的蓬勃发展,提高日活量成为媒体平台追求的重要目标之一。日活量的增加不仅意味着更广泛的影响力,还能为媒体平台带来更多的商业机会。以下是一些有效的策略,可帮助媒体提高日活量: admaoyan猫眼聚合 内容优质化&#…...

es6新特性总结
1、支持了let和const,为了防止var声明变量带来的变量提升 (1)、存在块级作用域不存在变量提升(考虑暂时性死区) (2)、不允许重复声明(包括普通变量和函数参数)变量提升…...

Spring Boot + hutool 创建海报图片
Spring Boot hutool 创建海报图片 /*** 分享,生成图片* param id* return*/GetMapping("/getShareImg")public void getShareImg(String id,HttpServletResponse response) throws IOException {CouponConsignSaleClassify byId couponConsignSaleClassifyService…...
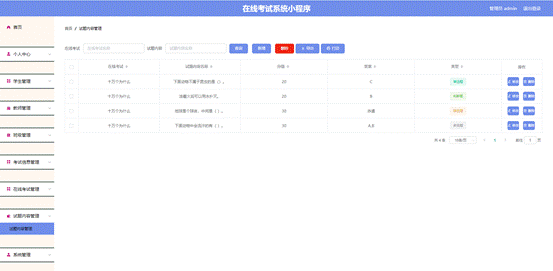
0002Java程序设计-springboot在线考试系统小程序
文章目录 **摘 要****目录**系统实现开发环境 编程技术交流、源码分享、模板分享、网课分享 企鹅🐧裙:776871563 摘 要 本毕业设计的内容是设计并且实现一个基于springboot的在线考试系统小程序。它是在Windows下,以MYSQL为数据库开发平台&…...
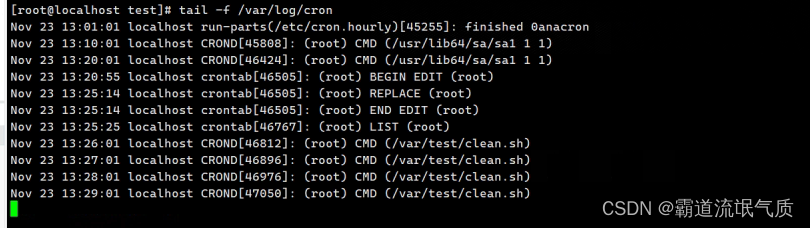
Linux(Centos)上使用crontab实现定时任务(定时执行脚本)
场景 Windows中通过bat定时执行命令和mysqldump实现数据库备份: Windows中通过bat定时执行命令和mysqldump实现数据库备份_mysqldump bat-CSDN博客 上面讲windows中使用bat实现定时任务的方式,如果是在linux上可以通过crontab实现。 cron是服务名称。…...

【Leetcode合集】20. 有效的括号
20. 有效的括号 20. 有效的括号 代码仓库地址: https://github.com/slience-me/Leetcode 个人博客 :https://slienceme.xyz 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串…...
)
OpenGL 绘制线(Qt)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里同样对OpenGL中的绘制线操作进行封装,便于后续的操作,很多形状也都是基于线来生成的,如圆形等。 二、实现代码 LineDrawable.h #ifndef LINE_DRAWABLE_H #define LINE_DRAWABLE_H#include...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
