前缀和——238. 除自身以外数组的乘积

文章目录
- 🍷1. 题目
- 🍸2. 算法原理
- 🍥解法一:暴力求解
- 🍥解法二:前缀和(积)
- 🍹3. 代码实现
🍷1. 题目
题目链接:238. 除自身以外数组的乘积 - 力扣(LeetCode)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法, 且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
进阶: 你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
🍸2. 算法原理
本题的意思是,要求出除了当前下标位置,其他位置的乘积

🍥解法一:暴力求解
暴力求解就是遍历整个数组,然后再遍历一次除了当前位置的其他位置元素乘积,整个的时间复杂度为O(n2)
🍥解法二:前缀和(积)
这里求除了当前位置的整个数组的乘积,可以理解为求前面一部的前缀积+后面一部分的后缀积
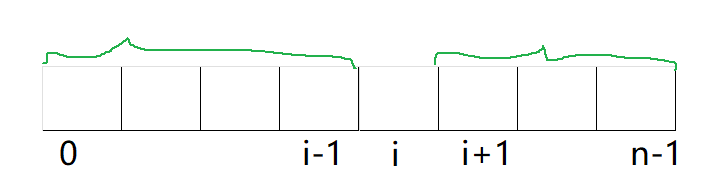
预处理:
f表示前缀积,f[i]表示[0,i-1]区间内所有元素的乘积f[i] = f[i-1] * nums[i-1]g表示后缀积,g[i]表示[i+1,n-1]区间内所有元素的乘积g[i] = g[i+1] * nums[i+1]
这里因为
f[i]的区间是[0,i-1],所以这里的i,实际上是i-1
使用预处理之后的数组:
有了预处理的数组,我们只需让f[i]*g[i]即可求出当前位置的值
细节问题:
这里因为要求的是乘积,所以
f[0]这里要提前处理一下,f[0] = 1;同理g[n-1] = 1。
f是从前往后,g是从后往前
这个时间复杂度为O(n)+O(n)+O(n),可理解为O(n)
这里进阶是空间复杂度为O(1)求解,采用的也是前缀积和后缀积,用
ret先装前缀积,然后从后往前乘以后缀积。
我们前面采用2个数组装前缀积和后缀积,可以理解得更清晰一些。
🍹3. 代码实现
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums){int n = nums.size();vector<int> f(n) , g(n);//预处理前缀积f[0] = 1;g[n-1] = 1;for(int i=1;i<n;i++)f[i] = f[i-1] * nums[i-1];//预处理后缀积for(int i=n-2;i>=0;i--)g[i] = g[i+1] * nums[i+1];vector<int> ret(n);for(int i=0;i<n;i++)ret[i]=f[i]*g[i];return ret;}
};
优化空间复杂度:
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums){int n = nums.size();vector<int> ret(n,1);int left = 1;for(int i=1;i<n;i++){left *= nums[i-1];ret[i] = left;}int right = 1;for(int i=n-2;i>=0;i--){right*=nums[i+1];ret[i]*=right;}return ret;}
};
相关文章:

前缀和——238. 除自身以外数组的乘积
文章目录 🍷1. 题目🍸2. 算法原理🍥解法一:暴力求解🍥解法二:前缀和(积) 🍹3. 代码实现 🍷1. 题目 题目链接:238. 除自身以外数组的乘积 - 力扣&a…...
)
MySql数据库常用指令(二)
MySql数据库常用指令(二) 一、WHERE 子句二、UPDATE 更新三、DELETE 语句四、LIKE 子句五、UNION 操作符 注:文中TEST为测试所用数据库,根据实际应用修改 一、WHERE 子句 SELECT 语句使用 WHERE 子句从数据表中读取数据…...

zookeeper 单机伪集群搭建简单记录
1、官方下载加压后,根目录下新建data和log目录,然后分别拷贝两份,分别放到D盘,E盘,F盘 2、data目录下面新建myid文件,文件内容分别为1,2,3.注意文件没有后缀,不能是txt文…...
【Linux】匿名管道与命名管道,进程池的简易实现
文章目录 前言一、匿名管道1.管道原理2.管道的四种情况3.管道的特点 二、命名管道1. 特点2.创建命名管道1.在命令行上2.在程序中 3.一个程序执行打开管道并不会真正打卡 三、进程池简易实现1.makefile2.Task.hpp3.ProcessPool.cpp 前言 一、匿名管道 #include <unistd.h&g…...
HTML5+ API 爬坑记录
背景: 有个比较早些使用5开发的项目, 最近两天反馈了一些问题, 解决过程在此记录; 坑1: plus.gallery.pick 选择图片没有进入回调 HTML5 API Reference 在 联想小新 平板电脑上选择相册图片进行上传时, 打开相册瞬间 应用会自动重启, 相册倒是有打开, 不过应用重启了, 导…...

idea git将某个分支内的commit合并到其他分支
idea git将某个分支内的commit合并到其他分支 1.打开旧分支的代码提交记录 在IDEA中切换到新分支的代码,点击Git打开代码管理面板,在顶部点击Log:标签页(这个标签页内将来可以选择不同分支的个人/所有人的代码commit记录)&#x…...
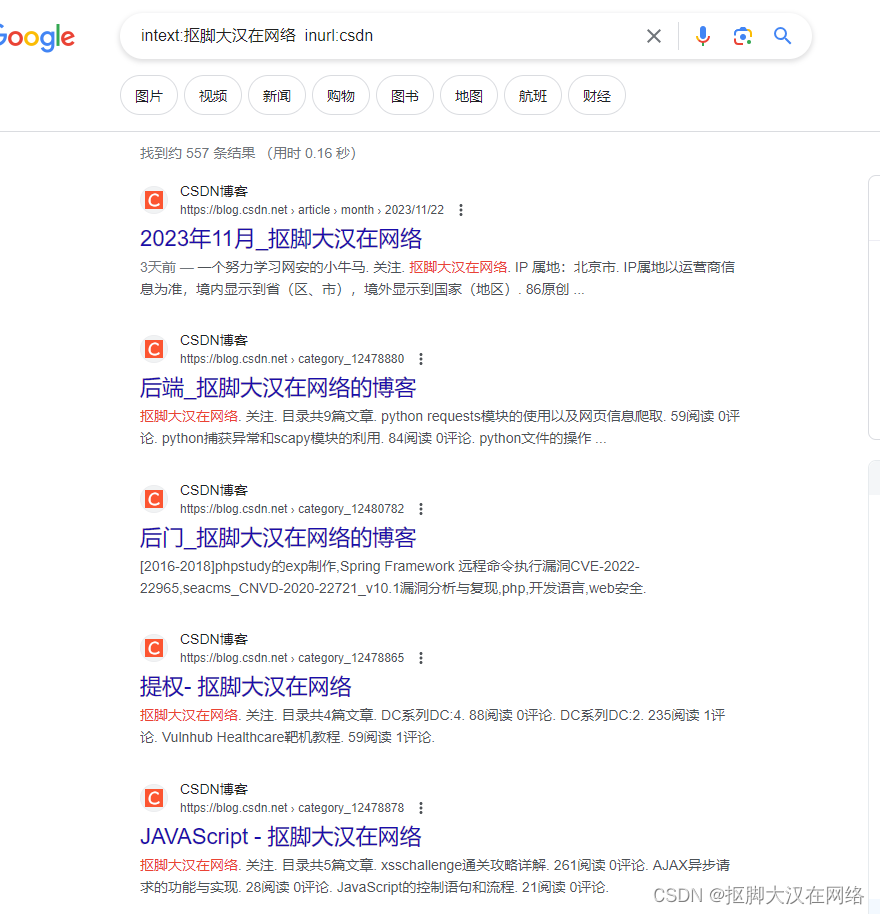
Google hacking语法
Google hacking语法 文章目录 Google hacking语法site:inurl:intitle:filetypecacheintext注意 site: 搜索子域 跟域名site:www.baidu.com 定位 跟语言 site: jp inurl: 用于在特定url链接中搜索网站信息 inurl:login intitle: 使用intitle:指令返回页面标题中包含关键…...
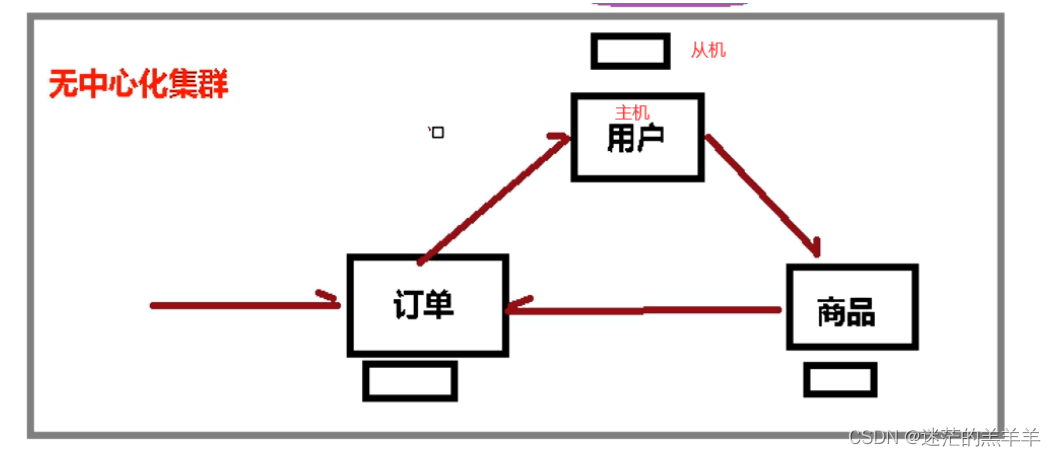
Redis集群(新)
1.什么是集群 Redis集群实现了对Redis的水平扩容,可实现并发写操作,启动n个redis节点,将数据分别存储在不同的节点中,每块节点负责不同区域的插槽,所以Redis集群通过分区来提供一定程度的可用性。 Redis集群现采用的是…...

[JVM] 常用调优参数
随着Java应用程序的不断发展和优化,JVM调优已经变得越来越重要。在这篇文章中,我们将探讨一些常用的JVM调优参数,了解如何更好地优化Java应用程序的性能。 文章目录 1. -Xmx2. -Xms3. -XX:PermSize和-XX:MaxPermSize4. -XX:NewRatio5. -XX:Ma…...
和4.输出部分(线性层、softmax层))
【nlp】3.5 Transformer论文复现:3.解码器部分(解码器层)和4.输出部分(线性层、softmax层)
Transformer论文复现:3.解码器部分(解码器层)和4.输出部分(线性层、softmax层) 3.1 解码器介绍3.2 解码器层3.2.1 解码器层的作用3.2.2 解码器层的代码实现3.2.3 解码器层总结3.3 解码器3.3.1 解码器的作用3.3.2 解码器的代码实现3.3.3 解码器总结4.1 输出部分介绍4.2 线性…...
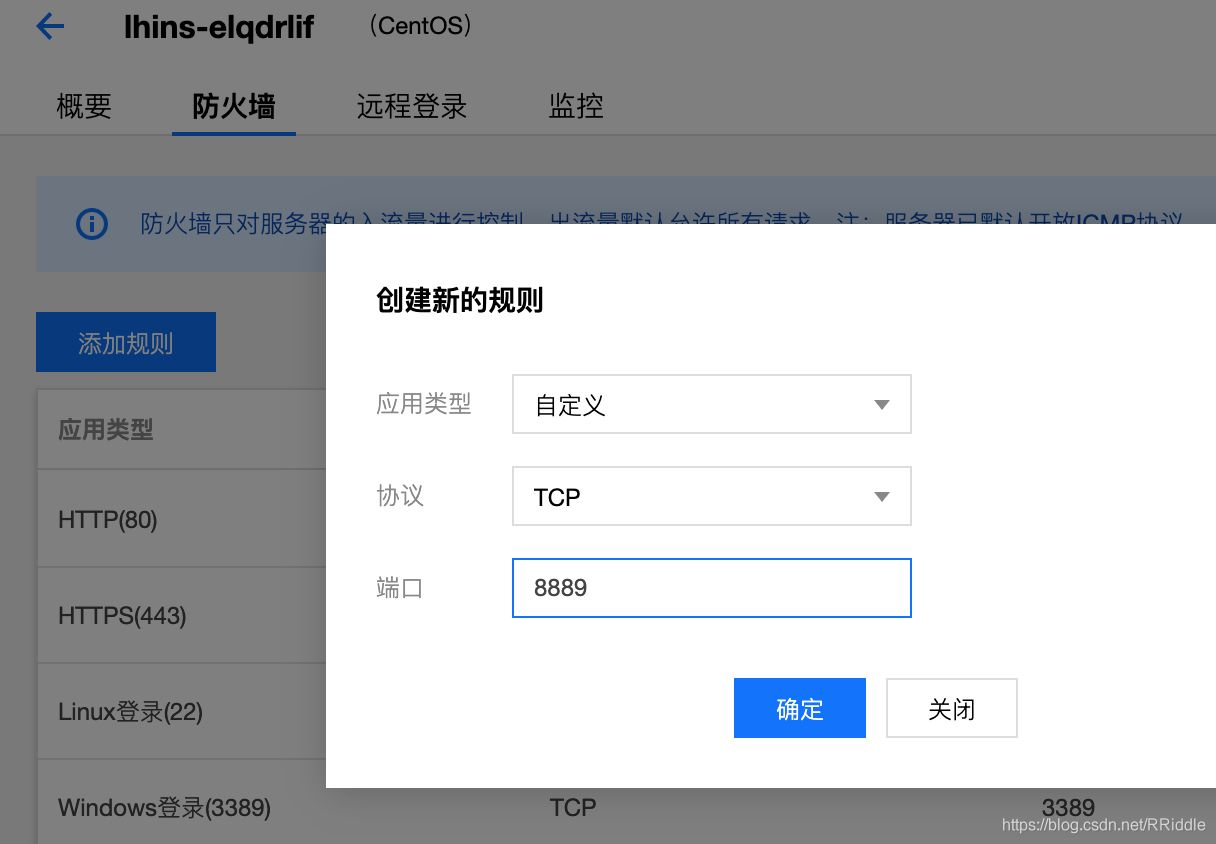
宝塔 Linux 面板安装一个高大上的论坛程序 —— Flarum
这个是很早搭建的版本,基于宝塔面板,比较复杂,如果想要简单的搭建方法,可以参看咕咕新写的这篇: 【好玩的 Docker 项目】10 分钟搭建一个高大上的论坛程序 购买腾讯云轻量应用服务器 待补充 登录服务器 待补充 BBR 加速脚本 BBR 加速脚本: BASH cd /usr/src &…...

数字化转型如何赋能企业实现数字化增值?
随着科技的不断发展,数字化转型已经成为了企业营销的重要趋势。数字化转型不仅可以提高企业的运营效率,还可以更好地满足消费者的需求,提升企业的市场竞争力。 一、数字化转型可以提高企业营销的精准性 在传统的企业营销中,营销人…...
)
深度学习之九(Transformers)
Transformers 是一种用于处理序列数据的深度学习模型,特别擅长于自然语言处理(NLP)任务。Transformer 是一种基于自注意力机制(Self-Attention Mechanism)的架构,于2017年由 Vaswani 等人在 “Attention is All You Need” 论文中提出,它在机器翻译任务中取得了显著的性…...
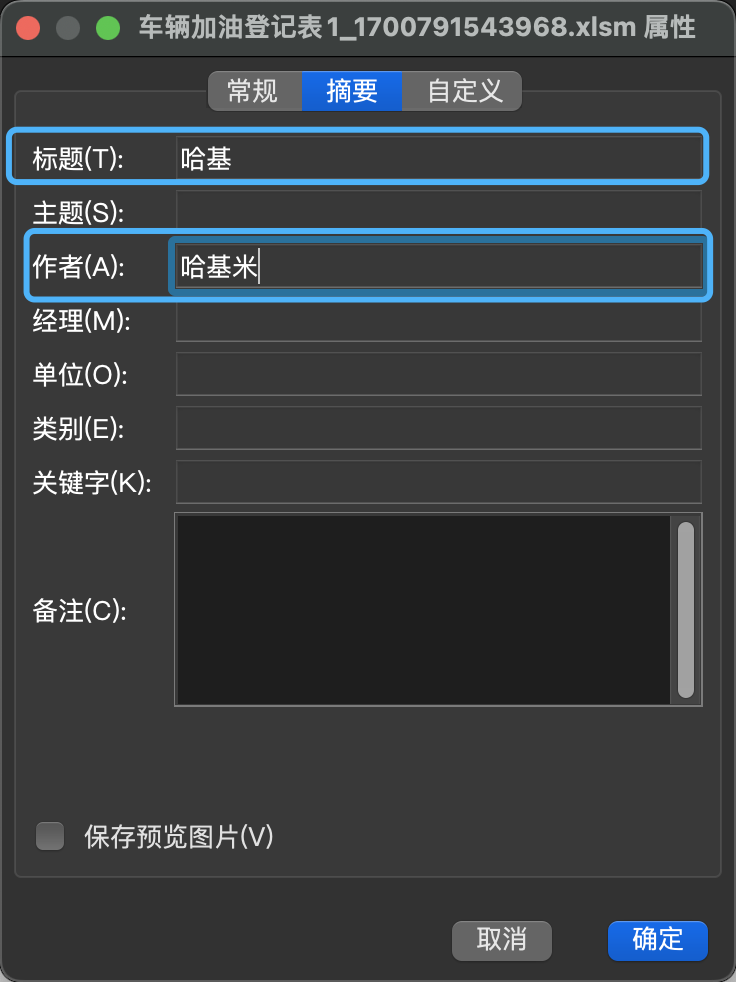
pgz easyexcel如何给excel文件添加自定义属性
免费API方式 直接上传URL,自定义修改Excel 视频演示【内含接口地址】 https://www.ixigua.com/7304510132812153385 前情提示 | 功能说明 多选仅支持微软office、office365系列Excel。因为WPS宏功能需要企业版且付费生成xlsx、xlsm等文件,office和WPS均可以打开,均可以单…...

【unity实战】实现一个放置3d物品建造装修系统(附项目源码)
文章目录 最终效果前言绘制开始场景素材开始放置旋转物体扩展优化1. 绘制地图边界,确保放置物品在指定区域内工作2. 让模型所占面积大小更加准确3. 隐藏白色瓦片指示区域 最终效果其他源码参考完结 最终效果 前言 其实3d物品建造装修系统之前就已经做过了ÿ…...
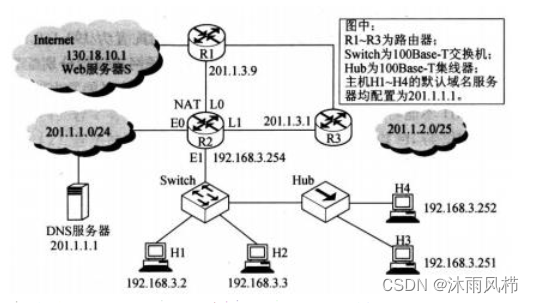
计算机网络之应用层
一、概述 引入目的: 为了方便用户去使用; 该如何方便用户使用网络呢,即怎样帮助用户使用网络? 1.用户需要知道网络资源所在的位置 2.网络上资源一定是在资源子网的主机上 3.资源子网上的主机,在通信子网中用IP地…...

Let’s xrOS 一款让你优先体验社区创作者的 visionOS App工具
Let’s xrOS Apple Vision Pro 发布预示着空间计算时代的到来,让科技爱好者和开发者开始思考如何在新的交互、系统和硬件上打造独特的三维应用。 自 WWDC 2023 的发布会后,社交媒体上涌现了许多精美的 visionOS App 的效果图和演示视频,然而…...
武汉教育E卡通学生证照片尺寸要求及证件照集中采集方法
”武汉教育E卡通“电子学生证旨在数字化中小学生身份,提供通用的教育卡,实现身份认证的电子化、权威化和集成化。校内一卡通系统包括刷卡考勤、电子班牌、图书借阅等,全面记录学生在校业务。同时,采集社会通行、实践活动等数据&am…...

C++《i+1》系列文章汇总
欢迎来到 PaQiuQiu 的空间 本文为【C《i1》专栏目录】,方便大家更好的阅读! 🚀~写在前面~ 当今计算机科学领域中最受欢迎和广泛使用的编程语言之一就是C。C是一种高级编程语言,具有强大的功能和广泛的应用领域,包括系统级编程、游…...
GEE:通过将 Landsat 5、7、8、9 的 C02 数据集合并起来,构建 NDVI 长时间序列
作者:CSDN @ _养乐多_ 本文记录了在 Google Earth Engine(GEE)平台上,将 Landsat-5、Landsat-7、Landsat-8 和 Landsat-9 的数据合成为一个影像集合,并生成 NDVI(归一化植被指数)的时间序列的代码。 代码封装成了函数,方便调用,结果如下图所示, 在实际应用中,可能…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...