「最优化基础知识2」一维搜索,以及python代码
最优化基础知识(2)
无约束优化问题,一维搜索
一、一维搜索
一维搜索的意思是在一个方向上找到最小点。
用数学语言描述,X*=Xk +tPk,从Xk沿着Pk方向行走t到达最小点X*。
1、收敛速度:
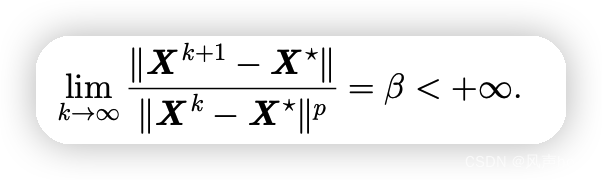
- 线性收敛:p=1,0<beta<1
- 超线性收敛: p>1或者beta=0
- 次线性收敛:p=1,beta=1
- p阶收敛:p>1
2、二次终止性:
能够在有限步内找到具有正定矩阵的二次函数的极小点。
f (X) = 1/2 XTAX + bTX + c
3、终止准则
什么时候停机,什么时候停止搜索。通常有以下五种:
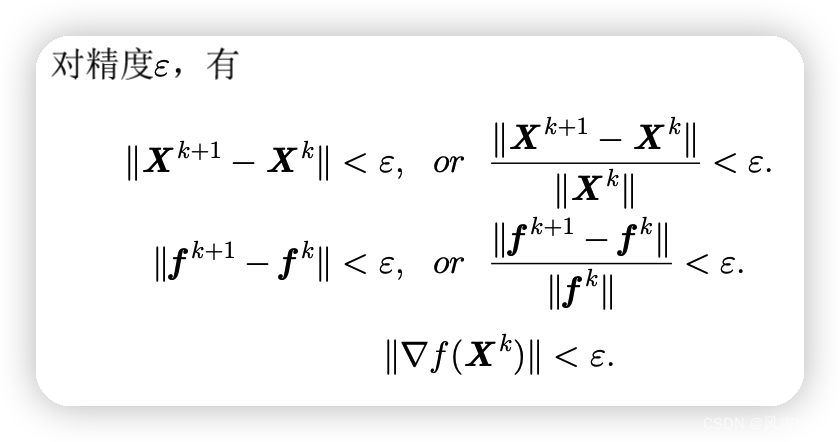
1、黄金分割法
给定每次迭代区间缩小比例,如果做才能搜索次数最少?
黄金分割法的python代码:
import mathdef golden_section_search(f, a, b, tol=1e-6):golden_ratio = (math.sqrt(5) - 1) / 2length = b - ax1 = a + (1 - golden_ratio) * lengthx2 = a + golden_ratio * lengthwhile x2-x1>tol:print(x1,x2)if f(x1) < f(x2):b = x2x2 = x1x1 = a + (1 - golden_ratio) * (b - a)else:a = x1x1 = x2x2 = a + golden_ratio * (b - a)return (a + b) / 2# 示例用法
def f(x):# 定义函数 f(x)return x*math.log(x)# 在区间 [0, 5] 中寻找函数的极小值点
result = golden_section_search(f, 0, 5)
print(f"极小值点的位置为: {result}")
print(f"函数极小值为: {f(result)}")
2、fibonacci搜索
给定迭代次数,如何在迭代次数内达到最好的搜索效果(最后一次迭代完成,搜索区间最小)?
这个问题可以反过来理解,假设最后一次迭代完成,搜索区间长度为1,那么最开始的搜索区间最大为多少?
python代码:
import mathdef fibonacci_search(f, a, b, n):# 计算Fibonacci数列fibonacci = [0, 1]for i in range(n):fibonacci.append(fibonacci[-1] + fibonacci[-2])# 计算初始区间长度length = b - a# 计算初始比例ratio = (fibonacci[-3] / fibonacci[-1]) if len(fibonacci) > 2 else 0# 初始化区间端点x1 = a + ratio * lengthx2 = a + (1 - ratio) * length# 迭代搜索for _ in range(len(fibonacci) - 3):if f(x1) < f(x2):b = x2x2 = x1x1 = a + ratio * (b - a)else:a = x1x1 = x2x2 = a + (1 - ratio) * (b - a)fibonacci.pop()ratio = (fibonacci[-3] / fibonacci[-1])print(fibonacci[-3],fibonacci[-1],ration)# 返回最优解的位置return (a + b) / 2# 示例用法
def f(x):# 定义函数 f(x)return x*math.log(x)# 在区间 [-5, 5] 中寻找函数的极小值点
result = fibonacci_search(f, 0, 5, 30)
print(f"极小值点的位置为: {result}")
print(f"函数极小值为: {f(result)}")
在有的地方,直接给出的不是迭代次数,而是最终的区间长度的上界L,b1-a1是初始区间。
b n − a n = F n − 1 / F n ( b n − 1 − a n − 1 ) = F n − 1 F n F n − 2 F n − 1 ⋯ F 1 F 2 ( b 1 − a 1 ) b_n-a_n=F_{n-1}/F_{n}(b_{n-1}-a_{n-1}) = \frac{F_{n-1}}{F_{n}}\frac{F_{n-2}}{F_{n-1}}\cdots\frac{F_{1}}{F_{2}}(b_1-a_1) bn−an=Fn−1/Fn(bn−1−an−1)=FnFn−1Fn−1Fn−2⋯F2F1(b1−a1)
也就是说区间长度最小bn-an=(b1-a1)/F_n<=L,F_n是最大的fibonacci数。
关键:F[n-2]+F[n-1]=F[n],F[n-2]/F[n]+F[n-1]/F[n]=1,这样能保证每次删掉一侧的区间,比例是一样的。
当F[6]/F[7]=21/34=0.6176470588235294,和黄金分割法近似相同。
黄金分割法是fibonacci法的极限形式。
3、三点二次插值法
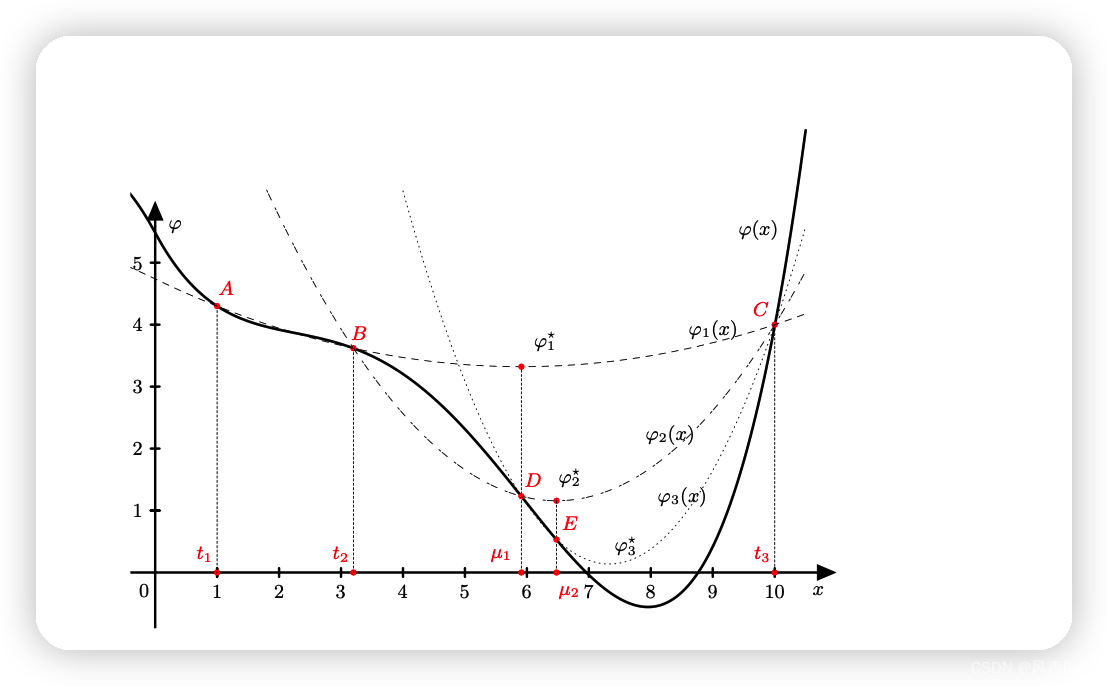
4、两点三次插值法

5、牛顿法
牛顿法就是在极小点附近选择一个初始点x0,在x0处二阶泰勒展开,并求其驻点。牛顿法不具有全局收敛性,因此初始点的选择很重要,它只是向初始点附近的驻点靠近。

牛顿法的python代码:
import sympy as sp
def newton_method(f, x0, tol=1e-6, max_iter=100):f_d1 = f.diff()f_d2 = f_d1.diff()# 迭代搜索for _ in range(max_iter):# 计算导数值fx = f_d1.subs({x:x0})fxx = f_d2.subs({x:x0})# 更新搜索位置x1 = x0 - fx / fxx# 检查是否满足终止条件if abs(x1 - x0) < tol:break# 更新当前点x0 = x1# 返回搜索结果return x1# 示例用法
x = sp.Symbol('x')
f=x**3-4*x+5# 选择初始点
x0 = -10# 使用牛顿法搜索函数的极小值点
result = newton_method(f, x0)
print(f"极小值点的位置为: {result.n()}")
print(f"函数极小值为: {f.subs({x:result}).n()}")
二、非精确一维搜索
1、Goldstein准则
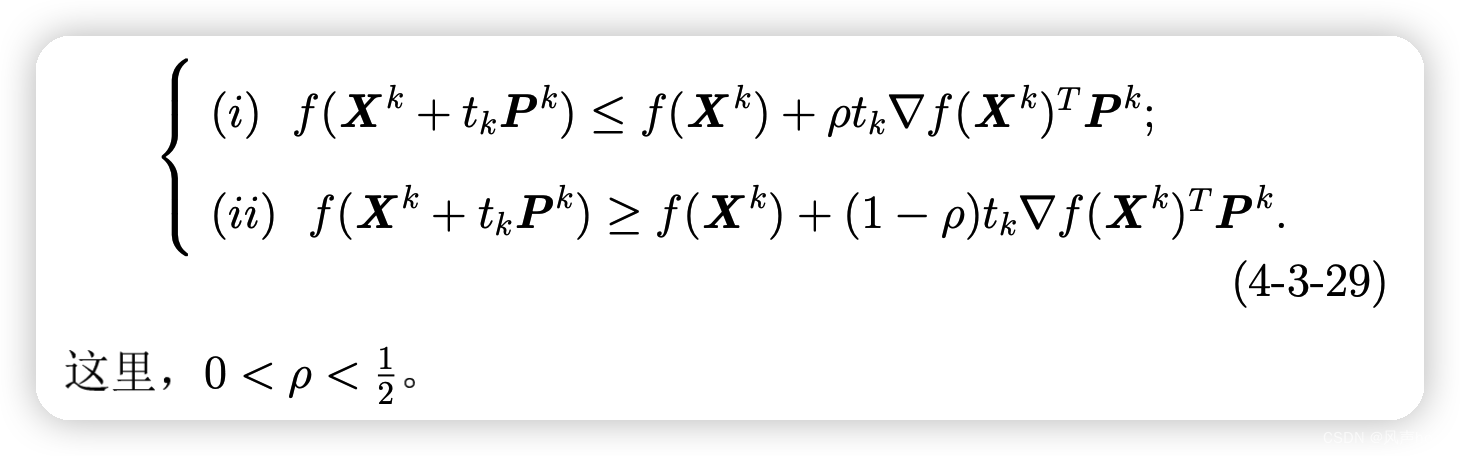
2、Wolfe准则

3、Armijo准则
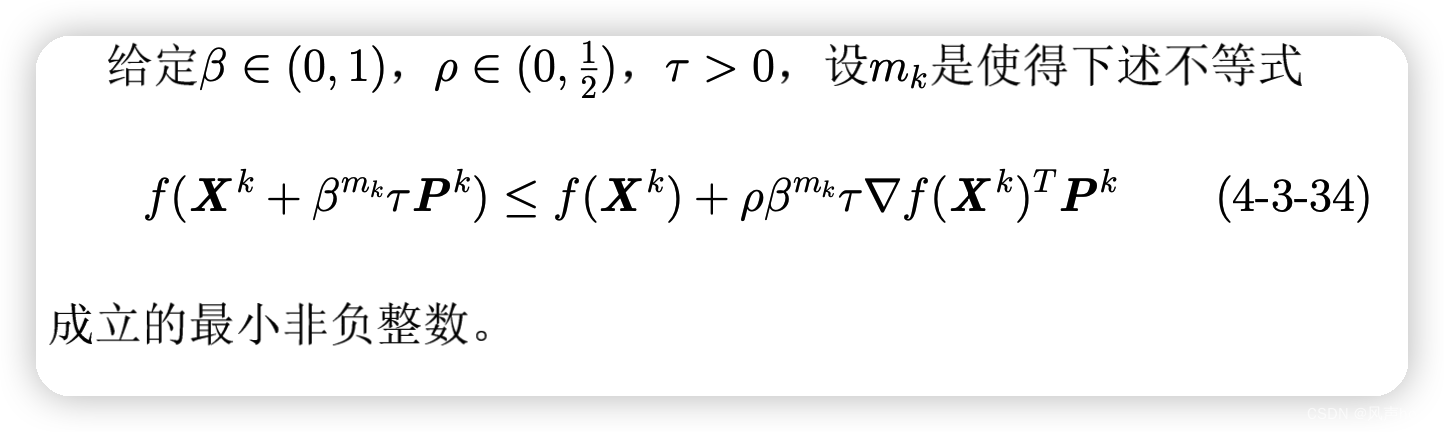
相关文章:
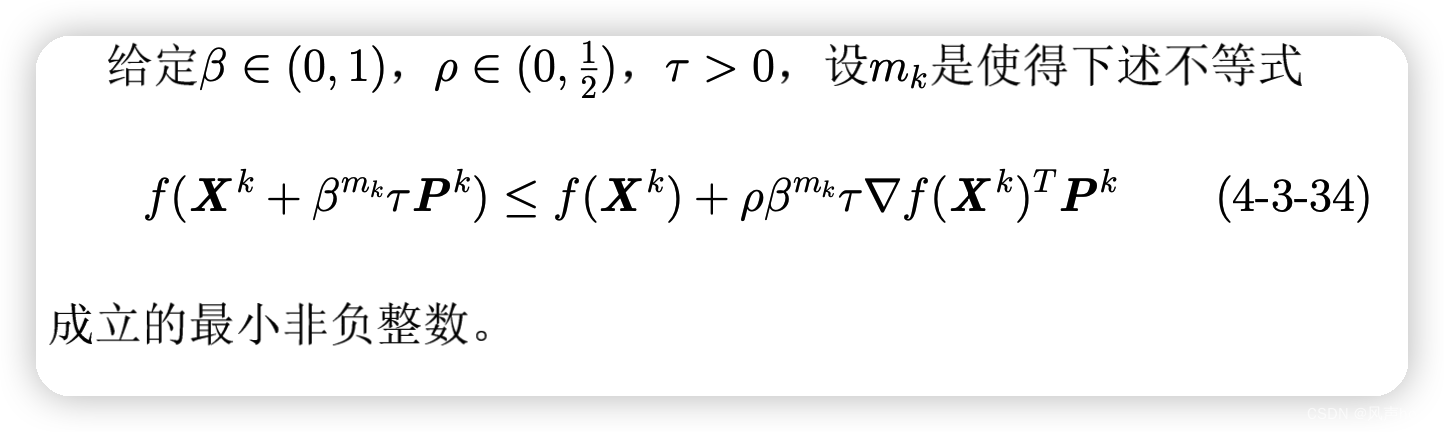
「最优化基础知识2」一维搜索,以及python代码
最优化基础知识(2) 无约束优化问题,一维搜索 一、一维搜索 一维搜索的意思是在一个方向上找到最小点。 用数学语言描述,X*Xk tPk,从Xk沿着Pk方向行走t到达最小点X*。 1、收敛速度: 线性收敛࿱…...
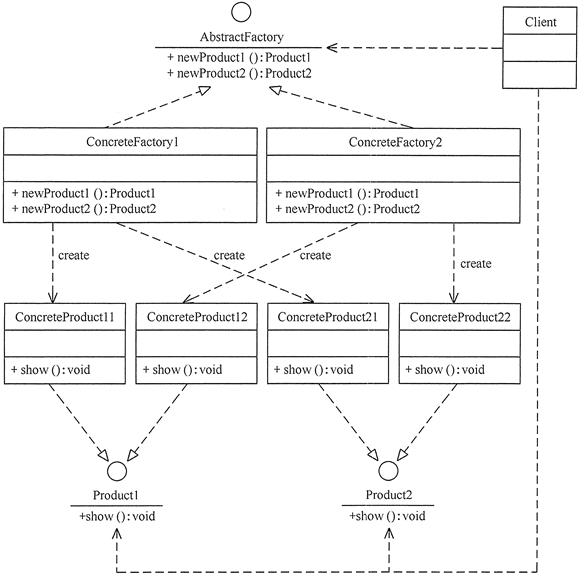
工厂模式之抽象工厂模式(常用)
抽象工厂模式 工厂方法模式中考虑的是一类产品的生产,如畜牧场只养动物、电视机厂只生产电视机、计算机软件学院只培养计算机软件专业的学生等。 同种类称为同等级,也就是说:工厂方法模式中只考虑生产同等级的产品,但是在现实生…...
Apache服务Rwrite功能使用
Rewrite也称为规则重写,主要功能是实现浏览器访问时,URL的跳转。其正则表达式是基于Perl语言。要使用rewrite功能,Apache服务器需要添加rewrite模块。如果使用源码编译安装,–enable-rewrite。有了rewrite模块后,需要在…...

【一起来学kubernetes】6、kubernetes基本概念区分
前言 前一篇文章我们对k8s中的一些常见概念进行了一个梳理,接下来我们将常见一些概念的区别和联系进行一个理解 service和deployment的区别和联系 在Kubernetes中,Service和Deployment是两个不同的概念,它们之间存在一定的关联。 Deployme…...
)
Python基础入门例程66-NP66 增加元组的长度(元组)
最近的博文: Python基础入门例程65-NP65 名单中出现过的人(元组)-CSDN博客 Python基础入门例程64-NP64 输出前三同学的成绩(元组)-CSDN博客 Python基础入门例程63-NP63 修改报名名单(元组)-CSDN博客 目录 最近的博文: 描述...
ubuntu22.04 安装 jupyterlab
JupyterLab Install JupyterLab with pip: pip install jupyterlabNote: If you install JupyterLab with conda or mamba, we recommend using the conda-forge channel. Once installed, launch JupyterLab with: jupyter lab...
探索移动端可能性:Capacitor5.5.1和vue2在Android studio中精细融合
介绍: 移动应用开发是日益复杂的任务,本文将带领您深入探索如何无缝集成Capacitor5.5.1、Vue2和Android Studio,以加速您的开发流程Capacitor 是一个用于构建跨平台移动应用程序的开源框架。Vue 是一个流行的 JavaScript 框架,用…...

【深度学习】Python快捷调用InsightFace人脸检测,纯ONNX推理
pypi资料: https://pypi.org/project/insightface/ 模型选择: https://github.com/deepinsight/insightface/tree/master/python-package#model-zoo onnxruntime的GPU对应CUDA : https://onnxruntime.ai/docs/reference/compatibility …...
JAVA序列化和反序列化
JAVA序列化和反序列化 文章目录 JAVA序列化和反序列化序列化什么是序列化?为什么要进行序列化?如何将对线进行序列化具体实现过程 完整代码 序列化 什么是序列化? 就是将对象转化为字节的过程 为什么要进行序列化? 让数据更高效的传输让数据更好的…...

基于浣熊算法优化概率神经网络PNN的分类预测 - 附代码
基于浣熊算法优化概率神经网络PNN的分类预测 - 附代码 文章目录 基于浣熊算法优化概率神经网络PNN的分类预测 - 附代码1.PNN网络概述2.变压器故障诊街系统相关背景2.1 模型建立 3.基于浣熊优化的PNN网络5.测试结果6.参考文献7.Matlab代码 摘要:针对PNN神经网络的光滑…...

uni-app打包后,打开软件时使其横屏显示
找到page.json文件,在global加入以下代码: 这样就可以横屏显示了。...

MYSQL基础知识之【创建,删除,选择数据库】
文章目录 前言MySQL 创建数据库使用 mysqladmin 创建数据库使用 PHP脚本 创建数据库 MySQL 删除数据库使用 mysqladmin 删除数据库使用PHP脚本删除数据库 MySQL 选择数据库从命令提示窗口中选择MySQL数据库使用PHP脚本选择MySQL数据库 后言 前言 hello world欢迎来到前端的新世…...

关于 token 和证书
关于 token 和证书 在网络检测中,Token通常是指一种特殊的令牌,用于在分布式系统中进行资源控制和访问管理。Token可以用于验证客户端的身份、限制客户端的访问权限以及控制客户端对某些资源的使用。 在网络检测中,Token通常用于以下几个方…...

基于SSM和微信小程序的场地预约网站
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SSM和微信小程序的场地预约网站,jav…...
——缺失的第一个正整数_困难)
Javascript每天一道算法题(十七)——缺失的第一个正整数_困难
文章目录 前言1、问题2、示例3、解决方法(1)方法1 总结 前言 提示: 1、问题 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 看了很久…...

【React】路径别名配置
路径解析配置(webpack),把 / 解析为 src/路径联想配置(VsCode),VSCode 在输入 / 时,自动联想出来对应的 src/下的子级目录 1. 路径解析配置 安装craco npm i -D craco/craco项目根目录下创建配…...

前缀和——238. 除自身以外数组的乘积
文章目录 🍷1. 题目🍸2. 算法原理🍥解法一:暴力求解🍥解法二:前缀和(积) 🍹3. 代码实现 🍷1. 题目 题目链接:238. 除自身以外数组的乘积 - 力扣&a…...
)
MySql数据库常用指令(二)
MySql数据库常用指令(二) 一、WHERE 子句二、UPDATE 更新三、DELETE 语句四、LIKE 子句五、UNION 操作符 注:文中TEST为测试所用数据库,根据实际应用修改 一、WHERE 子句 SELECT 语句使用 WHERE 子句从数据表中读取数据…...

zookeeper 单机伪集群搭建简单记录
1、官方下载加压后,根目录下新建data和log目录,然后分别拷贝两份,分别放到D盘,E盘,F盘 2、data目录下面新建myid文件,文件内容分别为1,2,3.注意文件没有后缀,不能是txt文…...
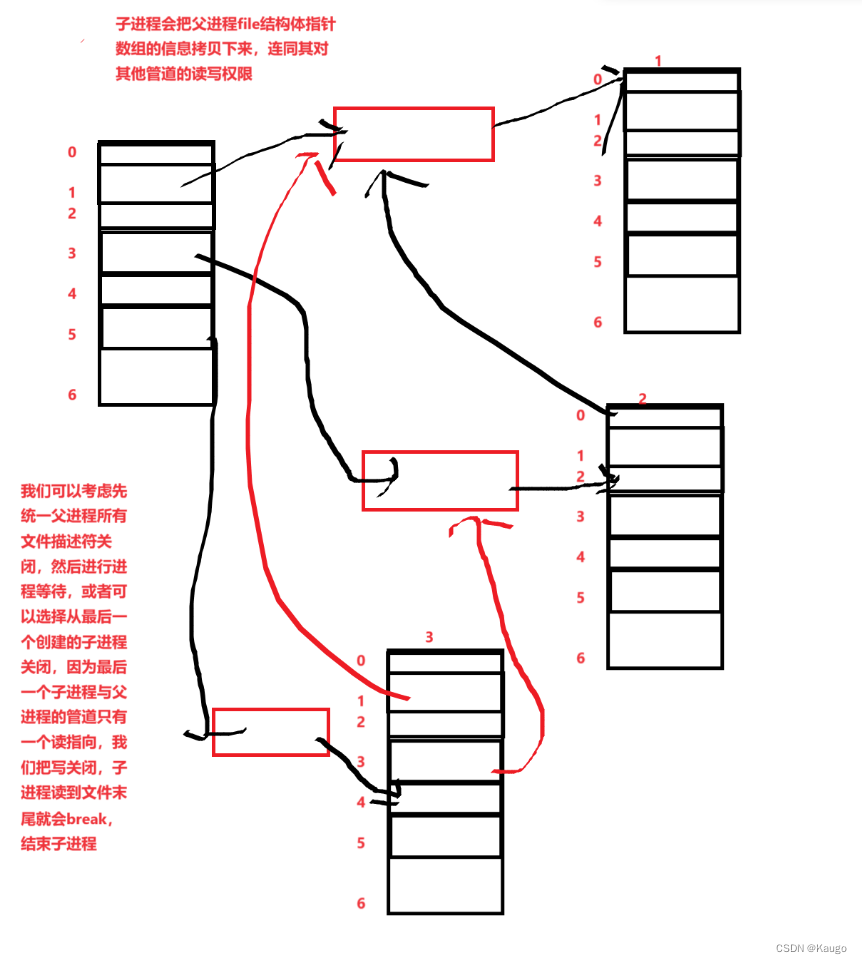
【Linux】匿名管道与命名管道,进程池的简易实现
文章目录 前言一、匿名管道1.管道原理2.管道的四种情况3.管道的特点 二、命名管道1. 特点2.创建命名管道1.在命令行上2.在程序中 3.一个程序执行打开管道并不会真正打卡 三、进程池简易实现1.makefile2.Task.hpp3.ProcessPool.cpp 前言 一、匿名管道 #include <unistd.h&g…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
