Javascript每天一道算法题(十八)——矩阵置零-中等
文章目录
- 1、问题
- 2、示例
- 3、解决方法
- (1)方法1——标记数组
1、问题
给定一个 y x x 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
2、示例
示例 1:
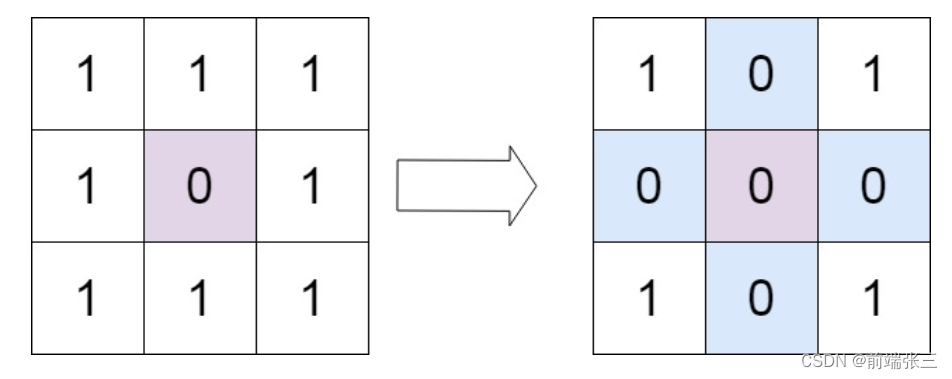
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
111 101
101 => 000
111 101
示例 2:
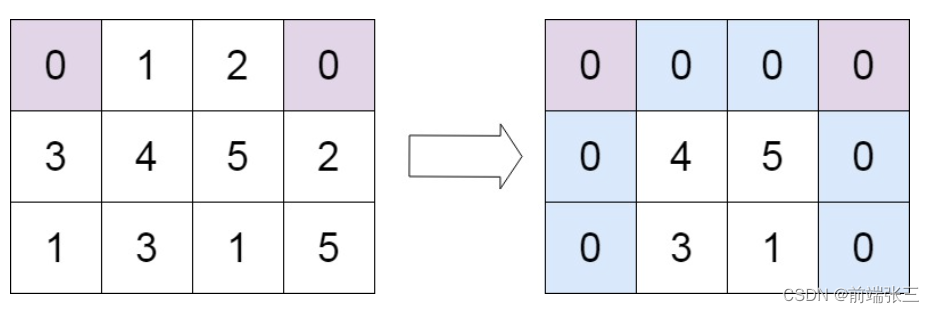
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
0120 0000
3452 => 0450
1215 0310
3、解决方法
(1)方法1——标记数组
思路:
1:用两个标记数组分别记录每一行和每一列是否有零出现。
2:遍历该数组一次,如果某个元素为 0,那么就将该元素所在的行和列所对应标记数组的位置置为 true
3:最后我们再次遍历该数组,用标记数组更新原数组即可。
let matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
var setZeroes = function(matrix) {// 1:获取x,y轴的长度let y = matrix.length; // 1-1:二维数组的长度(矩阵y轴的长度)let x = matrix[0].length; // 1-2:一维数组的长度(矩阵x轴的长度)// 2:获取行和列的长度(注意:行的长度由列决定)let row = new Array(y).fill(false); // 2-1: 行(行的长度是列的多少决定的,如示例二有四列,行为4)let col = new Array(x).fill(false); // 2-2: 列(列的长度是行的多少决定的,如示例二有三行,列为3)// 3:双层遍历该数组,如果其中有一个元素为0,将当前的行和列改为truefor(let i =0;i<y;i++){for(let j =0;j<x;j++){if(matrix[i][j] == 0){row[i] = col[j] = true}}}// 4:再次双层循环该数组,将之前标记为true的数据设置为0for(let i =0;i<y;i++){for(let j =0;j<x;j++){if(row[i] || col[j]){matrix[i][j] = 0}}}// 5:输出结果console.log('zz', matrix);
};
相关文章:
Javascript每天一道算法题(十八)——矩阵置零-中等
文章目录 1、问题2、示例3、解决方法(1)方法1——标记数组 1、问题 给定一个 y x x 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 2、示例 示例 1: 输入:matrix [[…...

基于ROS开发的开源项目
基于ROS (Robot Operating System) 开发的开源项目很多,其中一些已经在机器人领域内非常知名。以下是一些比较著名的例子: Autoware: Autoware 是一个开源的自动驾驶车辆的软件栈,提供了从3D地图表示、环境感知(如障碍物、行人检测…...
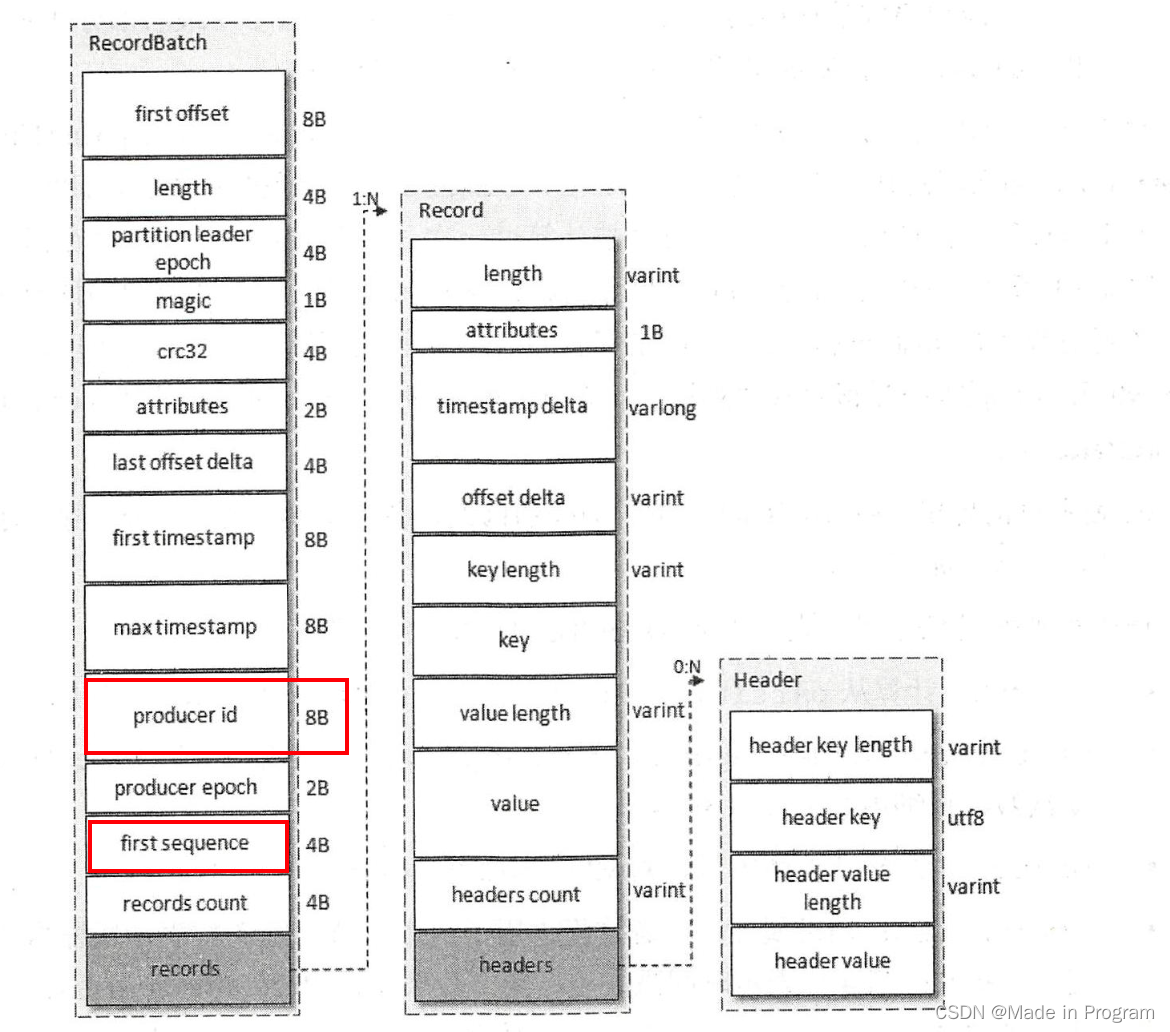
kafka精准一次、事务、幂等性
Kafka事务 消息中间件的消息保障的3个级别 At most once 至多一次。数据丢失。At last once 至少一次。数据冗余Exactly one 精准一次。好!!! 如何区分只要盯准提交位移、消费消息这两个动作的时机就可以了。 当:先消费消息、…...
centos 7.9 下利用miniconda里的pyinstaller打包python程序为二进制文件操作方法
centos 7.9 下利用miniconda里的pyinstaller打包python程序为二进制文件操作方法 一.centos 7.9 操作系统安装 参考:https://blog.csdn.net/qq_46015509/article/details/134572030?utm_sourceminiapp_weixin 安装完成后用后台连接工具连上虚拟机 二.安装python3 …...
Motion Plan之基于采样的路径规划算法笔记
Motion Plan之搜索算法笔记 背景: 基于采样算法是一种在路径规划中广泛应用的有效方法。它通过在图中随机选择点来生成一个简化的搜索图,从而加速搜索过程。这种方法的主要优点包括减少内存使用,避免计算错误,具有动态障碍物对抗…...

idea里面常用插件
这里列出了一系列常用的 IntelliJ IDEA 插件,它们可以提高开发效率、简化操作,以及帮助进行代码分析和优化。以下是每个插件的简要介绍: GenerateAllSetter:生成对象的所有 set 方法和 get 方法,方便对象之间的转换。该…...

回归算法优化过程推导
假设存在一个数据集,包含工资、年龄及贷款额度三个维度的数据。我们需要根据这个数据集进行建模,从而在给定工资和年龄的情况下,实现对贷款额度的预测。其中,工资和年龄是模型构建时的两个特征,额度是模型输出的目标值…...
某高品质房产企业:借助NineData平台,统一数据库访问权限,保障业务安全
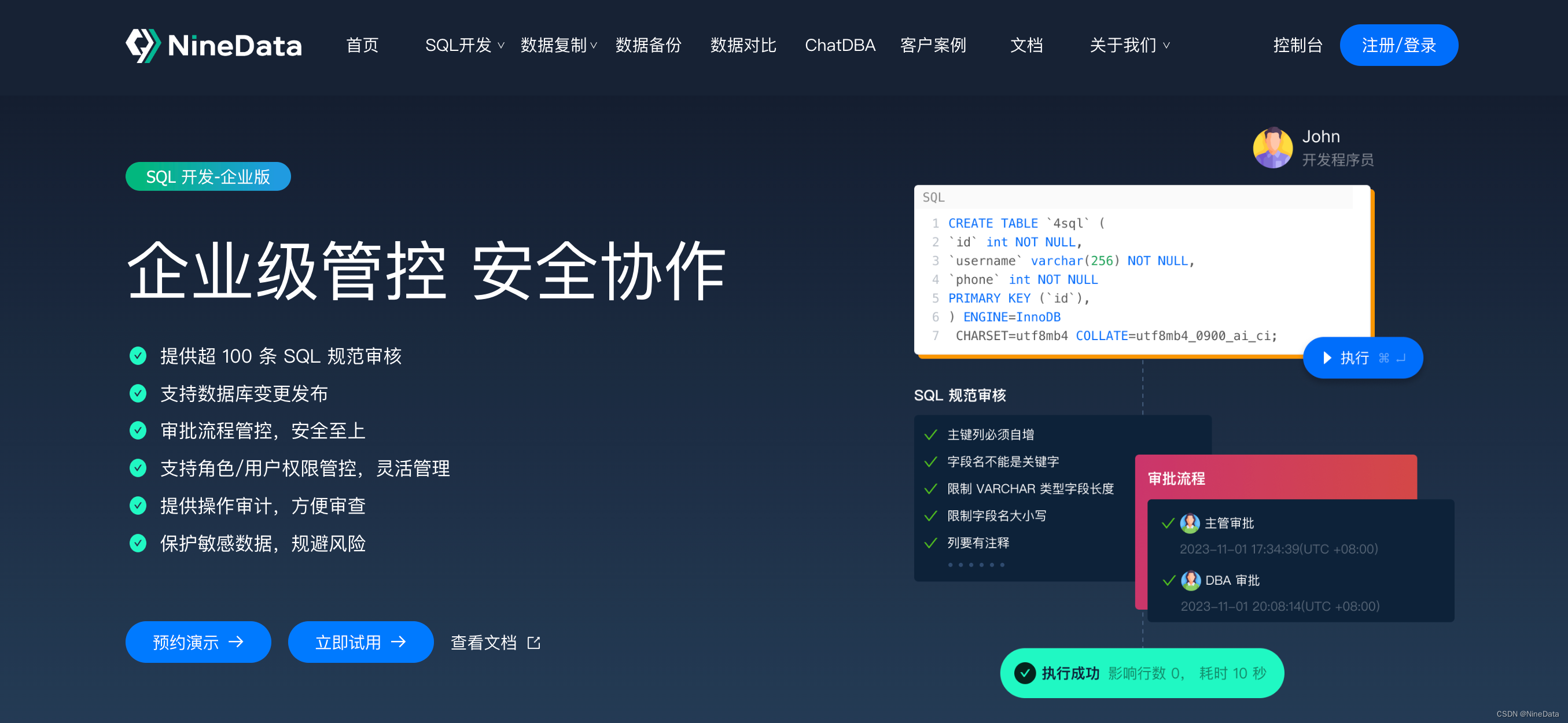
该企业是中国领先的优质房产品开发及生活综合服务供应商。在 2022 年取得了亮眼的业绩表现,销售额市场占有率跻身全国前五。业务涵盖房产开发、房产代建、城市更新、科技装修等多个领域。 2023 年,该企业和玖章算术(浙江)科技有限…...
Arduio开发STM32所面临的风险
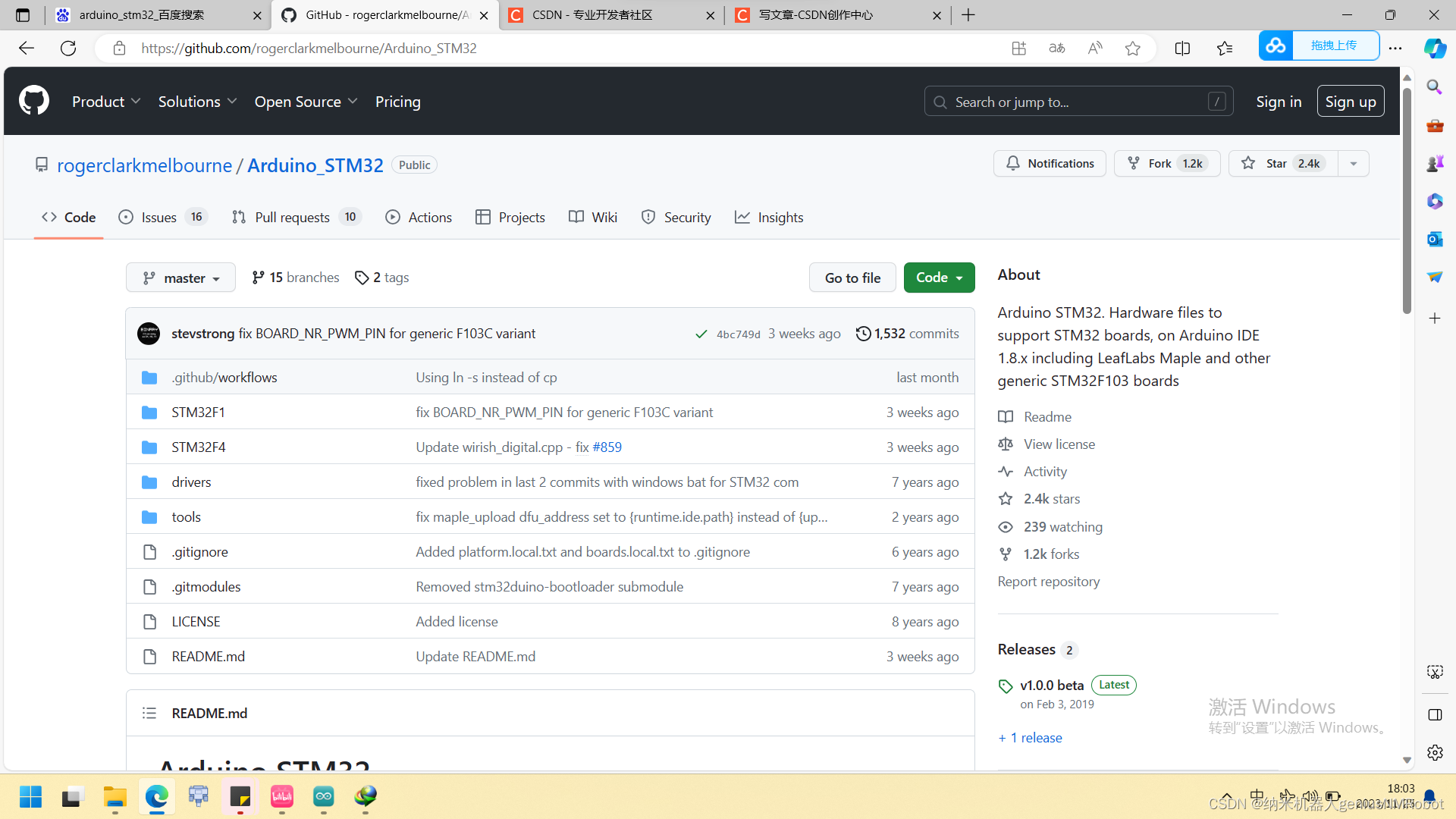
据说micro_ros用到了arduino,然后用arduino搞stm32需要用到这个Arduino STM32的东西,然后这里申明了:这些代码没有经过严格测试,如果是向心脏起搏器,自动驾驶这样要求严格的的情况下,这个东西不能保证100%不发生问题&a…...

精准人脉引流软件的开发流程与涉及到的技术
一、精准人脉引流软件的开发流程 1. 确定需求:首先,我们需要明确软件的需求,包括目标用户、功能需求、性能需求等。这些需求将直接影响到软件的开发方向和最终效果。 2. 系统设计:根据需求,进行系统设计,…...
Mysql数据库 20.DCL数据控制语言
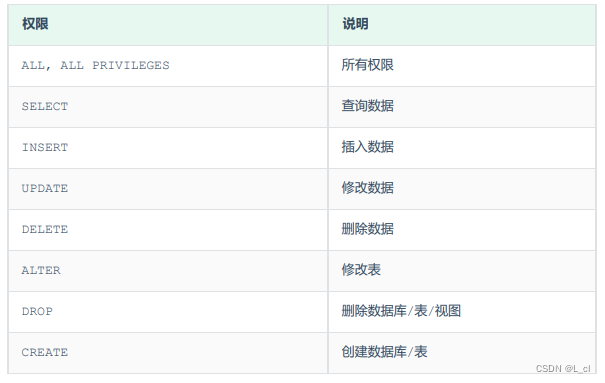
因这类SQL语言开发人员操作较少,主要是数据库管理员(DBA)使用,所以前文没有提及,这篇文章进行补充说明 DCL数据控制语言 用来管理数据库用户,控制数据库的访问权限 1.管理用户 1.1 查询用户 select * f…...

使用CMake交叉编译Arm Linux程序
下载安装aarch64-linux-gnu-gcc arm交叉编译工具链 apt-get install aarch64-linux-gnu-gccapt-get install aarch64-linux-gnu-gcc创建编译目录构建makefle 注意,工具链文件的指定一定要紧跟cmake命令之后,不能放到 … 后面构建arm架构cmake mkdir arm…...
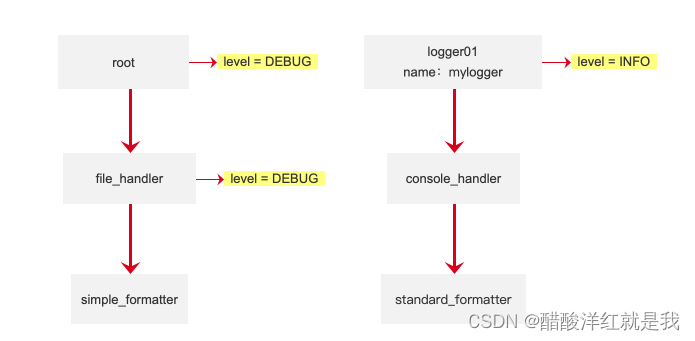
训练日志——logging
目录 基础使用日志的6个级别打印日志修改打印级别 高级应用logging的组成记录器Loggers处理器Handlers过滤器Filterformatter格式创建关联打印日志 配置文件参考 基础使用 日志的6个级别 打印日志 import logginglogging.debug(调试日志) logging.info(消息日志) logging.war…...
尺度为什么是sigma?
我们先看中值滤波和均值滤波。 以前,我认为是一样的,没有区分过。 他们说,均值滤波有使图像模糊的效果。 中值滤波有使图像去椒盐的效果。为什么不同呢?试了一下,果然不同,然后追踪了一下定义。 12345&…...

迭代器模式
自定义 Counter 结构体类型,并实现迭代器。其他语言的场景,读取数据库行数据时,使用的就是迭代器。我们使用for语言遍历数组,也是一种迭代。 结构体对象实现 Iterator trait,创建自定义的迭代器,只需要实现…...

C++ 修饰符、存储类、运算符、循环、判断
一、C修饰符类型: C允许在char、int、double数据类型前放置修饰符。 数据类型修饰符: ◆ signed:表示变量可以存储负数。对于整型变量来说,signed 可以省略,因为整型变量默认为有符号类型。 ◆ unsigned࿱…...
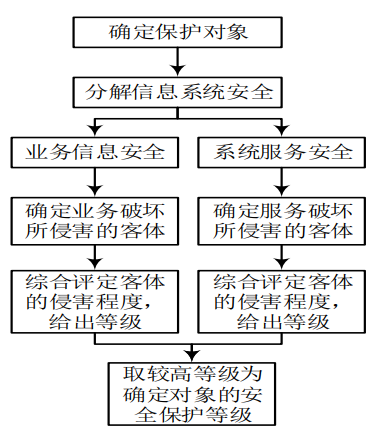
2023 hnust 湖南科技大学 信息安全管理课程 期中考试 复习资料
前言 ※老师没画重点的补充内容★往年试卷中多次出现或老师提过的,很可能考该笔记是奔着及格线去的,不是奔着90由于没有听过课,部分知识点不一定全,答案不一定完全正确 题型 试卷有很多题是原题 判断题(PPTÿ…...

N皇后问题解的个数
暴力递归 #include <stdio.h>int count0,a[15],flag; void queen(int,int); int main(){int n;scanf("%d",&n);queen(n,n);printf("%d",count); } void queen(int n,int n0){if(n<1){flag1;for(int i1;i<n0;i){for(int j1;j<n0;j){if(…...
php订单发起退款(余额和微信支付)
index.html <a class="btn btn-danger btn-change btn-tuikuan btn-disabled" href="javascript:;"><i class="fa fa-tuikuan"></i> 订单退款</a>-->order.js // 为表格绑定事件Table.api.bindevent(table);//退款…...
【SpringCloud】认识微服务、服务拆分以及远程调用
SpringCloud 1.认识微服务 1.1单体架构 单体架构:将业务的所有功能集中在一个项目中开发,打成一个包部署 单体架构的优缺点: 优点: 架构简单,部署成本低 缺点: 耦合度高(维护困难&#x…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果