量化交易:筹码理论的探索-筹码分布计算的实现
前言
很多朋友习惯了同花顺、大智慧等看盘软件,经常问到筹码分布如何计算。
说起来筹码分布的理论在庄股时代堪称是一个划时代产品,虽然历经level2数据、资金流统计、拆单算法与反拆单算法等新型技术的变革,庄股时代也逐渐淡出市场,但其背后的市场逻辑仍然具备一定的参考意义。
本篇就以BigQuant平台为基础,复现经典筹码理论的基础变量计算,为因子挖掘提供更多参考特征。
资金和筹码
资金是推动筹码移动的源动力,资金的强弱决定了筹码移动的方向。买入的资金强于卖出的筹码,说明筹码需求大于供应,股价就会上涨。相反,卖出的筹码强于买入的资金,说明筹码需求小于供应,股价就会下跌。当买入的力量和卖出的力量接近平衡时,说明供求相近,股价就会横盘震荡。筹码理论背后的经典逻辑
- 谁的筹码不抛
在筹码价位较高,没有明显出货迹象时,试想一只股票下跌了30%以上,而从没有放量,高端和低端筹码都不动,这是不正常的,散户重在散,下跌到一定程度一定会有很多人止损和出局,而持续盘跌不放量,只能说明其中有主力被套了,因为主力一般无法止损出局,那样成本太高了。这种股最适用于擒庄操作
- 谁的筹码不卖
在筹码价位较低时,一只股票上涨了20%以上,而从不放量,底端密集筹码不动也是不正常的,散户一般很少有人经得起如此引诱而一致不出货,这只能说明其中有主力在运做,而多数主力没有30%以上的利润是不会离场的,因为那样除去费用纯利就太低了。这种股最适用于坐轿操作。
- 机会和风险提示
有些股票虽然高位无量,但其拉升时出现了放量或长时间盘整,使筹码出现了高位集中,这些股一般是主力离场了,后市风险会较大。有些股低位放量或长时间盘整,出现筹码低位密集,一般是有主力进行收集造成的,操作起来机会比较大。
筹码理论的关键参数
- 筹码分布
计算历史所有筹码的换手价位,类似分价表 - 成本均线
以成交量为权重的价格平均线,用来表示N日内的市场参与者平均建仓成本。无穷成本平均线是最重要的成本均线,反映上市以来所有交易者的平均建仓成本,是市场牛熊的重要分水岭。 - 筹码集中度
刻画主要筹码堆积的主要区域的幅度,数值越大表示筹码集中的幅度越大,筹码就越分散。 - 活跃筹码
价附近的筹码是最不稳定的,也是最容易参与交易的,因为在股价附近的股票持有者,最经受不住诱惑,盈利的想赶快把浮动盈利换成实际盈利;被套的想趁着亏损得还少赶快卖掉,利用资金买另外的股票,把亏损赶快挣回来。而远离股价,在下方的筹码,由于有了一定的利润,持股信心会增强;在上方的筹码,由于被套太深而不愿割肉,所以在股价附近的筹码是最活跃的,而在股价上下,远离股价的筹码是不太活跃的。活跃筹码的数值很小时是很值得注意的一种情况。比如,一只股票经过漫长的下跌后,活跃筹码的值很小(小于10),大部分筹码都处于被套较深的状态,这时多数持股者已经不愿意割肉出局了,所以这时候往往能成为一个较好的买入点;再比如:一只股票经过一段时间的上涨,活跃筹码很小(小于10),大部分筹码都处于获利较多的状态,如果这时控盘强弱的值较大(大于20),前期有明显的庄股特征,总体涨幅不太大,也能成为一个较好的买入点。所以,在股价运行到不同的阶段时,考虑一下活跃筹码的多少,能起到很好的辅助效果。
筹码理论的股价周期阐述
股价走势循环周期的四个阶段
A阶段:无穷成本均线由向下到走平;俗称筑底阶段;
B阶段:无穷成本均线由走平到向上;俗称拉升阶段,可称为上升阶段;
C阶段:无穷成本均线由向上到走平;俗称作头(顶)阶段;
D阶段:无穷成本均线由走平到向下;俗称派发阶段,可称作下降阶段;1、筹码的价位分布计算
instruments = ['601700.SHA'] #这里尽量包含从上市日期开始到最后的数据 df = D.history_data(instruments, start_date='2005-01-02', end_date='2018-07-04', fields=['open','close','adjust_factor','turn','volume']) #获取历史数据 df['real_close']=df['close']/df['adjust_factor']#获取真实收盘价 df['real_open']=df['open']/df['adjust_factor']#获取真实开盘价 df['turn']=df['turn']/100#获取换手率 df['avg_price']=np.round(df['real_close']+df['real_open'])/2#计算每日平均成本,这里按照0.5元一个价位做分析 df=df.sort_values(by='date',ascending=False).reset_index(drop=True)#日期按降序排列 df['turn_tomo']=df['turn'].shift(1) #计算明日的换手率 df['remain_day']=1-df['turn_tomo'] #计算当日的剩余筹码比例 #假设N日后,上市第一天的剩余筹码比率就是每日剩余比例的累乘即:剩余筹码比例=(1-明天换手率)*(1-后日换手率)*...*(1-最新日换手率),以此类推各日的剩余筹码 df['remain_his']=df['remain_day'].cumprod()*df['turn'] df['remain_his']=df['remain_his'].fillna(df['turn'])#最新一日的筹码就是当日的换手率
#关键统计,统计最后一天的各价位历史筹码堆积量(百分比)
ss=df.groupby('avg_price')[['remain_his']].sum().rename(columns={'remain_his':'筹码量'})
ss.head(10)
| 筹码量 | |
|---|---|
| avg_price | |
| 3.5 | 0.060804 |
| 4.0 | 0.044996 |
| 4.5 | 0.120760 |
| 5.0 | 0.120956 |
| 5.5 | 0.059544 |
| 6.0 | 0.149679 |
| 6.5 | 0.075149 |
| 7.0 | 0.073177 |
| 7.5 | 0.069574 |
| 8.0 | 0.141947 |
#检查一下各价位筹码总和是不是1 ss['筹码量'].sum()
1.0000001
2、筹码理论的Winner指标
#计算end_date时某一价位的获利比例 pp=ss.reset_index() pp[pp.avg_price <=3.5]['筹码量'].sum()
0.06080448
#计算end_date时收盘价的获利比例 pp[pp.avg_price <=df['real_close'].iloc[-1]]['筹码量'].sum()
0.9996914
3、筹码理论的Cost指标
ss['筹码累积量']=ss['筹码量'].cumsum() ss.head()
| 筹码量 | 筹码累积量 | |
|---|---|---|
| avg_price | ||
| 3.5 | 0.060804 | 0.060804 |
| 4.0 | 0.044996 | 0.105800 |
| 4.5 | 0.120760 | 0.226561 |
| 5.0 | 0.120956 | 0.347516 |
| 5.5 | 0.059544 | 0.407060 |
#给定累计获利比率winner_ratio,计算对应的价位,表示在此价位上winner_ratio的筹码处于获利状态 winner_ratio=0.5 for i in range(len(ss)-1):if ss['筹码累积量'].iloc[i] < winner_ratio and ss['筹码累积量'].iloc[i+1]> winner_ratio:cost=ss.index[i] cost
5.5
4、计算全市场各股票的winner指标
instruments = ['601700.SHA','601699.SHA']
#这里尽量包含从上市日期开始到最后的数据
df = D.history_data(instruments, start_date='2005-01-02', end_date='2018-02-14',
fields=['open','close','adjust_factor','turn','volume']) #获取历史数据
df['real_close']=df['close']/df['adjust_factor']#获取真实收盘价
df['real_open']=df['open']/df['adjust_factor']#获取真实开盘价
df['turn']=df['turn']/100
df['avg_price']=np.round(df['real_close']+df['real_open'])/2#计算每日平均成本,这里按照0.5元一个价位做分析
df=df.sort_values(by='date',ascending=False).reset_index(drop=True)#日期按降序排列
df['turn_tomo']=df.groupby('instrument')['turn'].apply(lambda x:x.shift(1)) #计算明日的换手率
df['remain_day']=1-df['turn_tomo'] #计算当日的剩余筹码比例
#假设N日后,上市第一天的剩余筹码比率就是每日剩余比例的累乘即:剩余筹码比例=(1-明天换手率)*(1-后日换手率)*...*(1-最新日换手率),以此类推各日的剩余筹码
df['remain_his']=df.groupby('instrument')['remain_day'].apply(lambda x:x.cumprod())
df['remain_his']=df['remain_his']*df['turn']
df['remain_his']=df['remain_his'].fillna(df['turn'])#最新一日的筹码就是当日的换手率
#关键统计,统计最后一天的各价位历史筹码堆积量(百分比)
ss=df.groupby(['instrument','avg_price'])[['remain_his']].sum().rename(columns={'remain_his':'筹码量'}).reset_index()
real_close=df.groupby('instrument')[['real_close']].apply(lambda x:x.iloc[0]).reset_index()
pp=ss.merge(real_close,on='instrument')
#计算end_date时收盘价的获利比例
winner=pp[pp.avg_price<=pp.real_close].groupby('instrument')[['筹码量']].sum().rename(columns={'筹码量':'winner'})
winner
| winner | |
|---|---|
| instrument | |
| 601699.SHA | 0.639122 |
| 601700.SHA | 0.817013 |
#检查各股票各价位的筹码总和是否为1
ss.groupby('instrument')['筹码量'].sum()
instrument 601699.SHA 1.0 601700.SHA 1.0 Name: 筹码量, dtype: float32
计算全市场各股票每日的winner指标
instruments = ['601700.SHA','601699.SHA'] #这里尽量包含从上市日期开始到最后的数据 df_all = D.history_data(instruments, start_date='2005-01-02', end_date='2018-02-14', fields=['open','close','adjust_factor','turn','volume']) #获取历史数据
def cal_winner_day(df_all):winner=[]for k in list(df_all.date):df=df_all[df_all.date<=k]df['real_close']=df['close']/df['adjust_factor']#获取真实收盘价df['real_open']=df['open']/df['adjust_factor']#获取真实开盘价df['turn']=df['turn']/100#获取换手率df['avg_price']=np.round(df['real_close']+df['real_open'])/2#计算每日平均成本,这里按照0.5元一个价位做分析df=df.sort_values(by='date',ascending=False).reset_index(drop=True)#日期按降序排列df['turn_tomo']=df['turn'].shift(1)#计算明日的换手率df['remain_day']=1-df['turn_tomo'] #计算当日的剩余筹码比例#假设N日后,上市第一天的剩余筹码比率就是每日剩余比例的累乘即:剩余筹码比例=(1-明天换手率)*(1-后日换手率)*...*(1-最新日换手率),以此类推各日的剩余筹码df['remain_his']=df['remain_day'].cumprod()df['remain_his']=df['remain_his']*df['turn']df['remain_his']=df['remain_his'].fillna(df['turn'])#最新一日的筹码就是当日的换手率#关键统计,统计最后一天的各价位历史筹码堆积量(百分比)ss=df.groupby('avg_price')[['remain_his']].sum().rename(columns={'remain_his':'筹码量'}).reset_index()ss['real_close']=df['real_close'].iloc[0]#计算end_date时收盘价的获利比例winner_day=ss[ss.avg_price<=ss.real_close]['筹码量'].sum()winner.append(winner_day)result=pd.DataFrame({'winner':winner},index=df_all.date)return result
winner_all=df_all.groupby('instrument').apply(cal_winner_day)
winner_all.reset_index().sort_values(by='date',ascending=False).head()
| instrument | date | winner | |
|---|---|---|---|
| 4497 | 601700.SHA | 2018-02-14 | 0.817013 |
| 2773 | 601699.SHA | 2018-02-14 | 0.639122 |
| 2772 | 601699.SHA | 2018-02-13 | 0.518967 |
| 4496 | 601700.SHA | 2018-02-13 | 0.816618 |
| 2771 | 601699.SHA | 2018-02-12 | 0.530768 |
相关文章:

量化交易:筹码理论的探索-筹码分布计算的实现
前言 很多朋友习惯了同花顺、大智慧等看盘软件,经常问到筹码分布如何计算。 说起来筹码分布的理论在庄股时代堪称是一个划时代产品,虽然历经level2数据、资金流统计、拆单算法与反拆单算法等新型技术的变革,庄股时代也逐渐淡出市场…...

常用Redis的键命令参考
一、DEL DEL key [key …] 删除给定的一个或多个 key 。 不存在的 key 会被忽略。 #删除单个键127.0.0.1:6379> set name zhangsan OK 127.0.0.1:6379> del name (integer) 1# 删除一个不存在的 key, 失败,没有 key 被删除127.0.0.1:6379> E…...

Lombok @With 的纯弊端及如何避免
由于是第一篇写关于 Lombok 的日志,所以有些不情愿去开门见山直接触及 With, 而要先提一提本人对 Lombok 的接触过程。 两三年之前写 Java 代码一直都是全手工打造。一个数据类,所有必须的 setter/getter, toString, hashcode() 等全体现在源代码中&…...
无重复字符的最长字串)
C语言每日一题(38)无重复字符的最长字串
力扣 3 无重复字符的最长字串 题目描述 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s…...
Azure Machine Learning - Azure可视化图像分类操作实战
目录 一、数据准备二、创建自定义视觉资源三、创建新项目四、选择训练图像五、上传和标记图像六、训练分类器七、评估分类器概率阈值 八、管理训练迭代 在本文中,你将了解如何使用Azure可视化页面创建图像分类模型。 生成模型后,可以使用新图像测试该模型…...

PaddleOCR学习笔记
Paddle 功能特性 PP-OCR系列模型列表 https://github.com/PaddlePaddle/PaddleOCR#%EF%B8%8F-pp-ocr%E7%B3%BB%E5%88%97%E6%A8%A1%E5%9E%8B%E5%88%97%E8%A1%A8%E6%9B%B4%E6%96%B0%E4%B8%AD PP-OCR系列模型列表(V4,2023年8月1日更新) 配置文…...
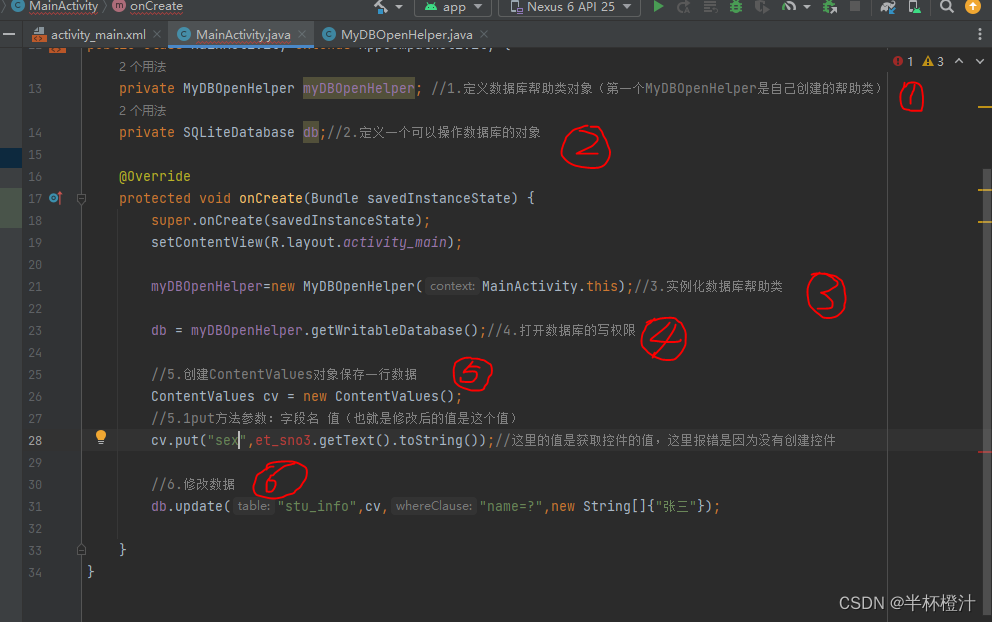
安卓用SQLite数据库存储数据
什么是SQLite? SQLite是安卓中的轻量级内置数据库,不需要设置用户名和密码就可以使用。资源占用较少,运算速度也比较快。 SQLite支持:null(空)、integer(整形)、real(小…...
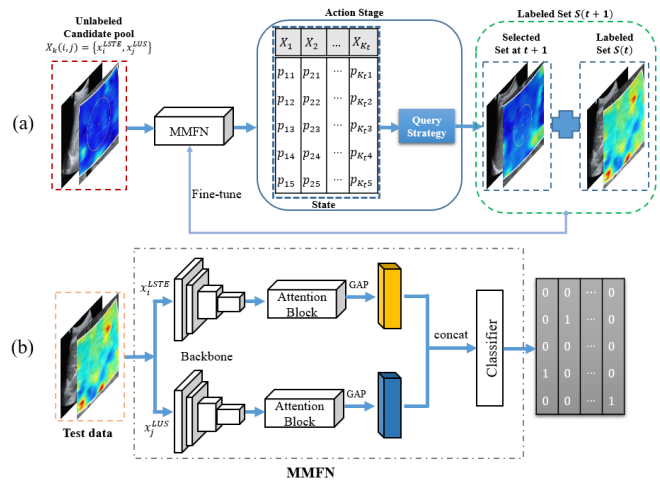
MMFN-AL
MMFN means ‘multi-modal fusion network’ 辅助信息 作者未提供代码...

7、独立按键控制LED状态
按键的抖动 对于机械开关,当机械触点断开、闭合时,由于机械触点的弹性作用,一个开关在闭合时不回马上稳定地接通,在断开时也不会一下子断开,所以在开关闭合及断开的瞬间会伴随一连串的抖动 #include <REGX52.H…...

香蕉派BPI-M4 Zero单板计算机采用全志H618,板载2GRAM内存
Banana Pi BPI-M4 Zero 香蕉派 BPI-M4 Zero是BPI-M2 Zero的最新升级版本。它在性能上有很大的提高。主控芯片升级为全志科技H618 四核A53, CPU主频提升25%。内存升级为2G LPDDR4,板载8G eMMC存储。它支持5G WiFi 和蓝牙, USB接口也升级为type-C。 它具有与树莓派 …...

微信小程序内部跳到外部小程序
要在微信小程序中跳转到外部小程序,可以使用wx.navigateToMiniProgram函数。以下是一个示例: wx.navigateToMiniProgram({appId: 外部小程序的appId,path: 外部小程序的路径,extraData: {id: xxx},success(res) {// 跳转成功} })在这个示例中࿰…...

Spring Boot中设置文件上传大小限制
在Spring Boot中,可以通过以下步骤来设置上传文件的大小: 在application.properties或application.yml文件中,添加以下配置: 对于application.properties: spring.servlet.multipart.max-file-size128MB spring.se…...

8、独立按键控制LED显示二进制
独立按键控制LED显示二进制 #include <REGX52.H>void Delay(unsigned int xms) //12.000MHz {unsigned char i, j;while(xms--){i 2;j 239;do{while (--j);} while (--i);} }void main() {//数据类型刚好是8位与51单片机IO口寄存器位数相同(默认高电平&am…...
命名空间、字符串、布尔类型、nullptr、类型推导
面向过程语言:C ——> 重视求解过程 面向对象语言:C ——> 重视求解的方法 面向对象的三大特征:封装、继承和多态 C 和 C 在语法上的区别 1、命名空间(用于解决命名冲突问题) 2、函数重载和运算符重载…...

力控软件与多台PLC之间ModbusTCP/IP无线通信
Modbus TCP/IP 是对成熟的 Modbus 协议的改编, 因其开放性、简单性和广泛接受性而在工业自动化系统中发挥着举足轻重的作用。它作为连接各种工业设备的通用通信协议,包括可编程逻辑控制器 (PLC)、远程终端单元 (RTU) 和传感器。它提供标准化的 TCP 接口&…...

第96步 深度学习图像目标检测:FCOS建模
基于WIN10的64位系统演示 一、写在前面 本期开始,我们继续学习深度学习图像目标检测系列,FCOS(Fully Convolutional One-Stage Object Detection)模型。 二、FCOS简介 FCOS(Fully Convolutional One-Stage Object D…...

常用的git命令完整详细109条
Git是一个很强大的分布式版本控制系统,以下是一些常用的git命令: git init:在当前目录下创建一个新的Git仓库。git add 文件名:将指定的文件添加到暂存区,准备提交。git commit -m “备注”:提交暂存区的文…...

Ansible的错误处理
环境 管理节点:Ubuntu 22.04控制节点:CentOS 8Ansible:2.15.6 ignore_errors 使用 ignore_errors: true 来让Ansible忽略错误(运行结果是 failed ): --- - hosts: alltasks:- name: task1shell: cat /t…...
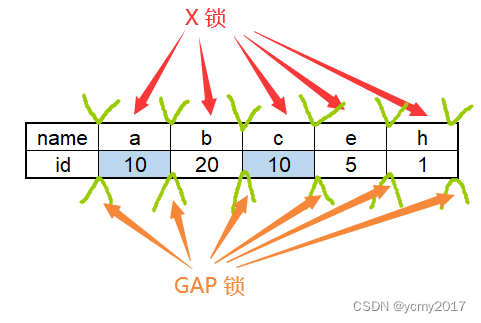
MySQL-04-InnoDB存储引擎锁和加锁分析
Latch一般称为闩锁(轻量级锁),因为其要求锁定的时间必须非常短。在InnoDB存储引擎中,latch又分为mutex(互斥量)和rwlock(读写锁)。 Lock的对象是事务,用来锁定的是…...

tcp/ip协议2实现的插图,数据结构2 (19 - 章)
(68) 68 十九1 选路请求与消息 函rtalloc,rtalloc1,rtfree (69) 69 十九2 选路请求与消息 函rtrequest (70)...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
