LeetCode算法题解|474. 一和零
474. 一和零
题目链接:474. 一和零
题目描述
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
算法分析:
之前的背包问题中对于背包的描述只有一种维度,那就是背包的容量。
而这道题需要对背包有两种约束维度,也就是0和1的个数m,n,我们可以看成是容量a和容量b。
而每一个字符串我们看作一个物品,它有两个属性,即0的个数和1的个数。
接下来我们按照动态规划五部曲来。
定义dp数组及下表含义:
对于dp[i][j],我们将其定义为容量a,b分别为i,j的背包,最多能装下的物品数量为dp[i][j]。
递推公式:
类似于一种维度背包的递推公式:dp[j]=max(dp[j],dp[j-weigth[i]+value[i]);
我们只需要将背包的一维属性变成二维就可以了:dp[i][j]=max(dp[i][j],dp[i-mNumb][j-nNumb]+1);
初始化:
dp[0][0]=0,容量a,b皆为0的背包所能装下的物品数量为0。
遍历顺序:
先遍历物品在遍历背包容量(对于背包容量的两种维度可以任意顺序遍历,但必须都是倒叙遍历)。
打印dp数组:
对于这道题dp数组的所表示的含义比较难理解,打印出来去推导验证的话也是比较困难的。
代码如下:
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];//dp[m][n]表示0的个数m,1的个数为n的集合的元素个数for(int i = 0; i < strs.length; i++) {//遍历每个元素int mNum = 0;//记录每个元素种0的个数int nNum = 0;//记录每个元素种1的个数for(int j = 0; j < strs[i].length(); j++) {if(strs[i].charAt(j) == '0') mNum++;else nNum++;}//倒叙遍历每个元素中0和1的个数for(int j = m; j >= mNum; j--) {for(int k = n; k >= nNum; k--) {dp[j][k] = Math.max(dp[j][k], dp[j - mNum][k - nNum] + 1);}}}return dp[m][n];}
}总结
这道题还是比较难的,对于背包的属性需要考虑两个维度(0的个数和1的个数),不过我们只需要将其看成容量a和容量b就可以了,还是01背包的思路。
相关文章:

LeetCode算法题解|474. 一和零
474. 一和零 题目链接:474. 一和零 题目描述 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子…...

一种太阳能风能市电互补路灯方案介绍
太阳能市电互补路灯是一种环保、节能的照明设施,它利用太阳能进行发电并实现照明。这种路灯在白天吸收阳光并将其转化为电能,到了晚上则利用储存的电能为LED灯提供电力,实现照明功能。下面叁仟智慧将详细介绍太阳能市电互补路灯灯的工作原理和…...

世微 dc-dc降压恒流 LED汽车大灯 单灯 14V5A 68W车灯驱动方案 AP5191
产品描述 AP5191是一款PWM工作模式,高效率、外围简单、外置功率MOS管,适用于4.5-150V输入的高精度降压LED恒流驱动芯片。输出最大功率150W,最大电流6A。AP5191可实现线性调光和PWM调光,线性调光脚有效电压范围0.55-2.6V.AP5191 工作频率可以…...
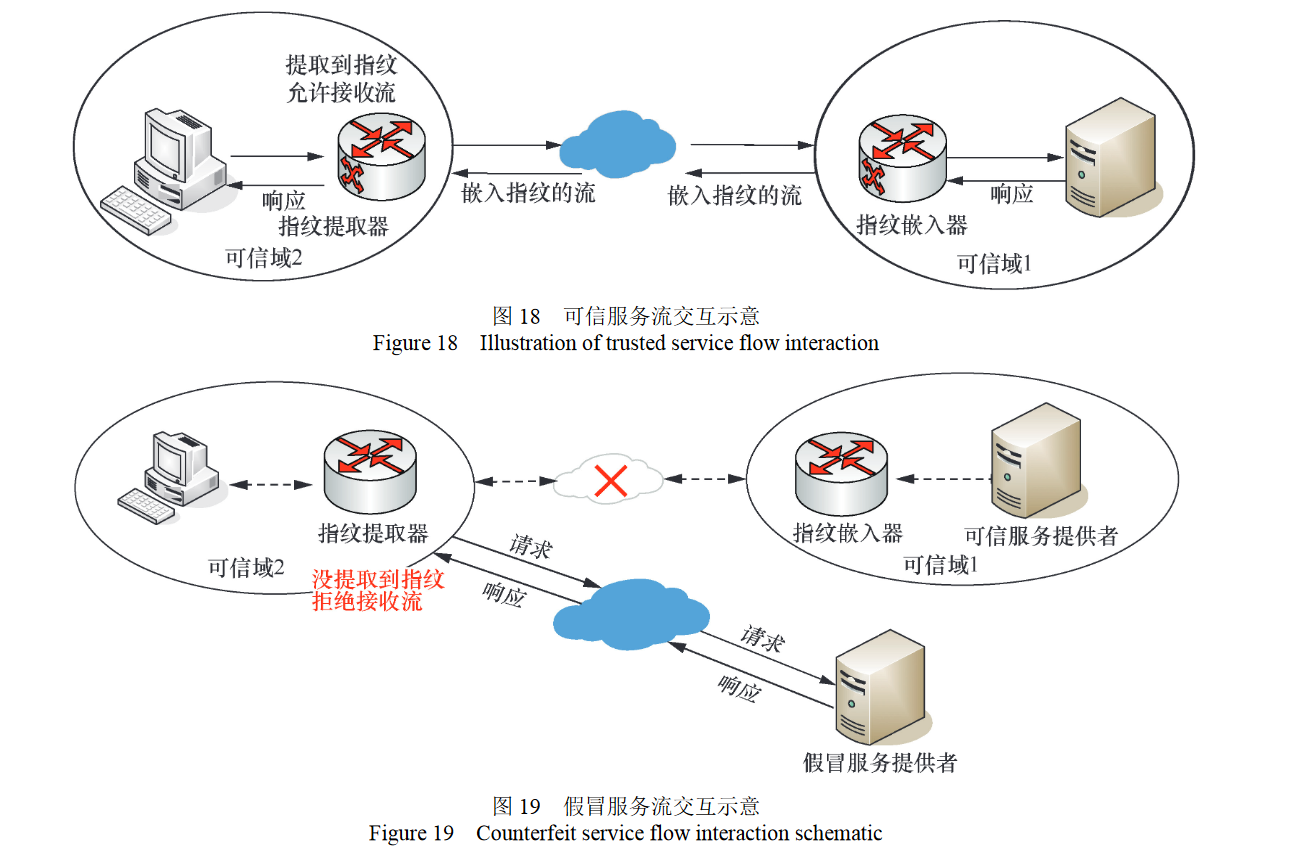
基于时隙的多重冗余流指纹模型
文章信息 论文题目:基于时隙的多重冗余流指纹模型 期刊(会议):网络与信息安全学报 时间:2023 级别:CCF C 概述 为确保内生网络流量安全可信,本文在研究流水印及其扩展的流指纹机制的基础上&a…...
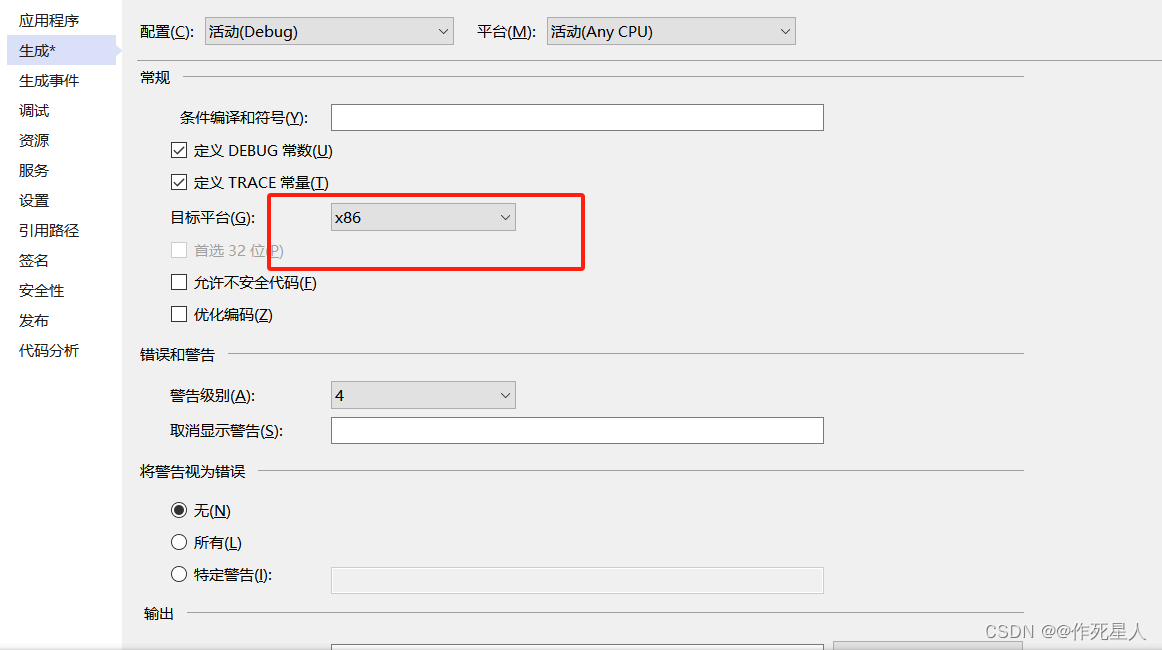
Visual Studio 2019 C# System.BadImageFormatException 解决方法
文章目录 1.DLL文件缺失或不匹配原因解决方法 2.系统环境变量Path下内容过多原因解决方法 3.位数错误原因解决方法 分析几种可能因素 1.DLL文件缺失或不匹配 原因 检查对应Debug路径下的DLL文件是否有缺失 解决方法 将对应的DLL文件放到Debug文件夹里面,检查冗余…...
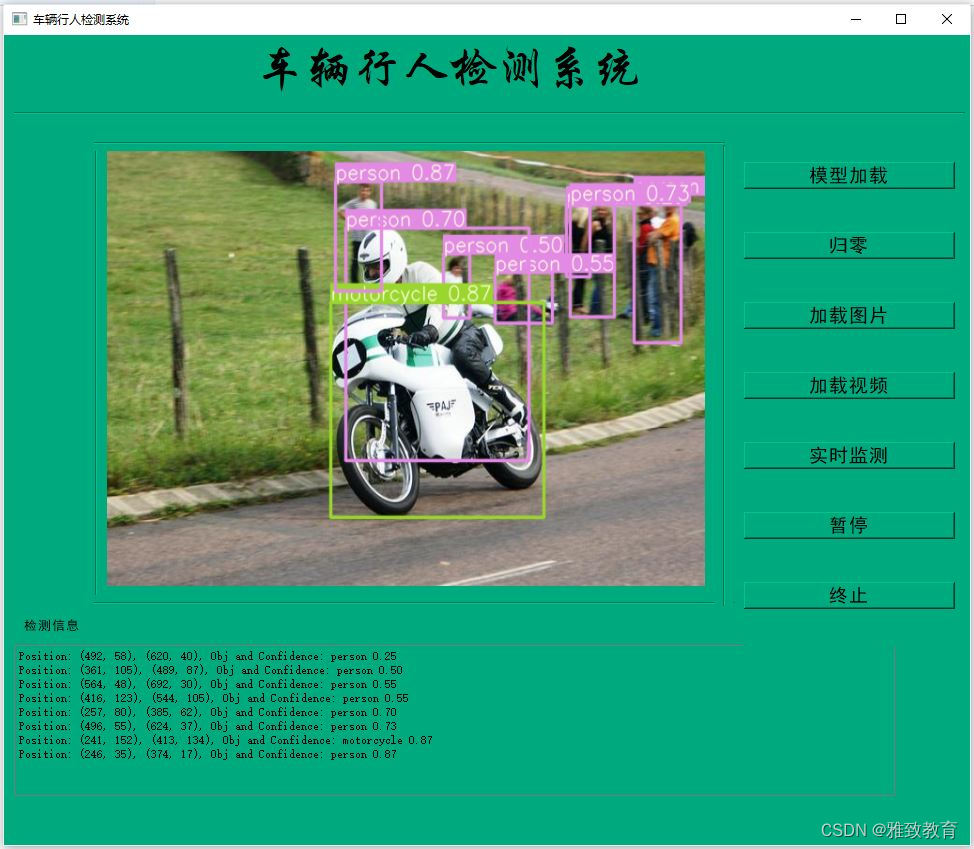
深度学习之基于YoloV5车辆和行人目标检测系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介YOLOv5 简介YOLOv5 特点 车辆和行人目标检测系统 二、功能三、系统四. 总结 一项目简介 # 深度学习之基于 YOLOv5 车辆和行人目标检测系统介绍 深度学习在…...
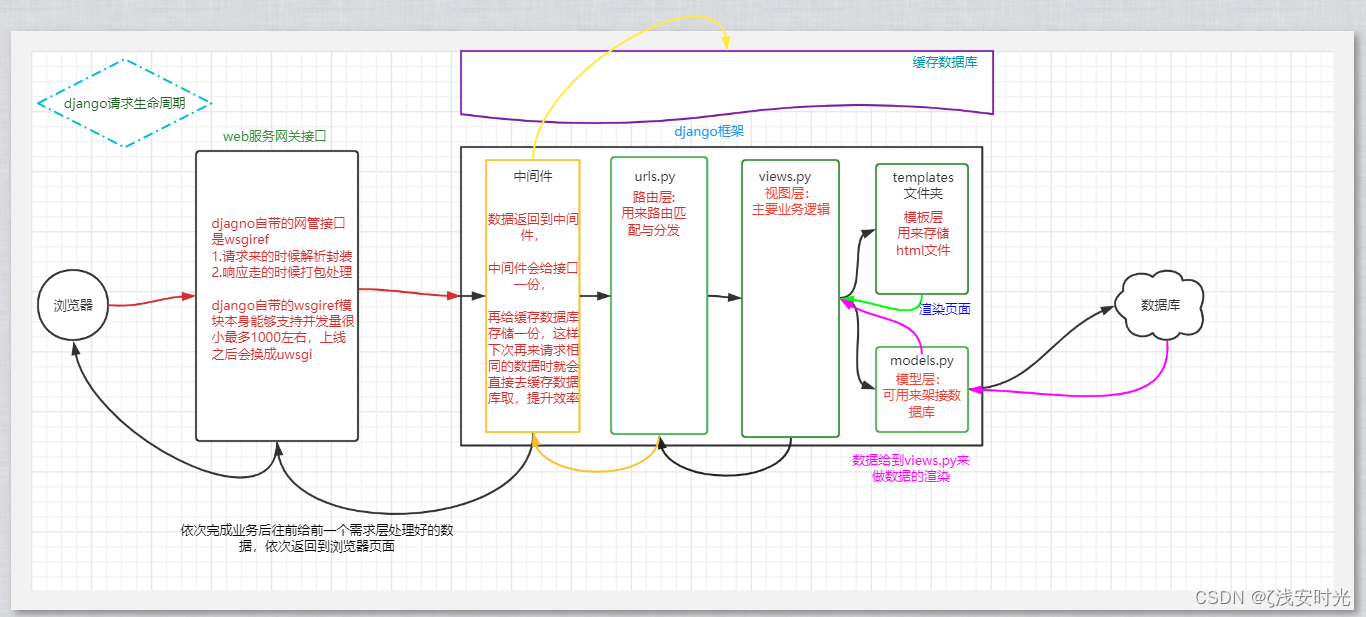
Django框架之中间件
目录 一、引入 二、Django中间件介绍 【1】什么是Django中间件 【2】Django中间件的作用 【3】示例 三、Django请求生命周期流程图 四、Django中间件是Django的门户 五、Django中间件详解 六、中间件必须要掌握的两个方法 (1) process_request (2) process_respon…...

BTC 复兴:Ordinals 带来创新活力,BitVM 与 BitStream 相继问世
除了备受瞩目的 ETF,今年 Bitcoin 生态迎来全新的发展活力和机遇。Ordinals 协议的横空出世,以此为基础诞生的 BRC20 协议给整个比特币生态带去了一波新的能量,迎来铭文热度高涨。而诸如 BitVM、BitStream 等新技术甫一问世,便引发…...
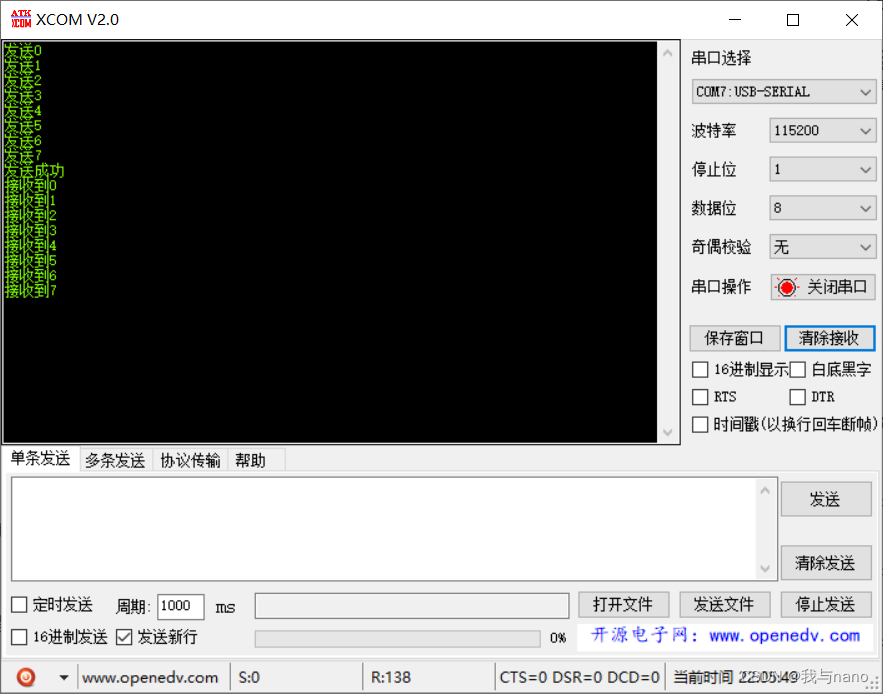
STM32 CAN协议讲解以及代码
STM32 CAN 文章目录 STM32 CAN前言一、CAN外设1.主控制寄存器CAN_MCR2.位时序寄存器CAN_BTR3.CAN的发送邮箱4.CAN的接收FIFO5.验收筛选器 二、代码配置1.初始化2.发送数据3.接收数据4.main.c 前言 前面学习了CAN的一些理论知识,他在我们的STM32里面是怎么用的呢 前…...

京东数据分析(京东大数据):2023年10月京东手机行业品牌销售排行榜
鲸参谋监测的京东平台10月份手机市场销售数据已出炉! 根据鲸参谋平台的数据显示,今年10月份,京东平台手机行业的销量约340万,环比增长约11%,同比则下滑约2%;销售额为108亿,环比增长约17%&#x…...
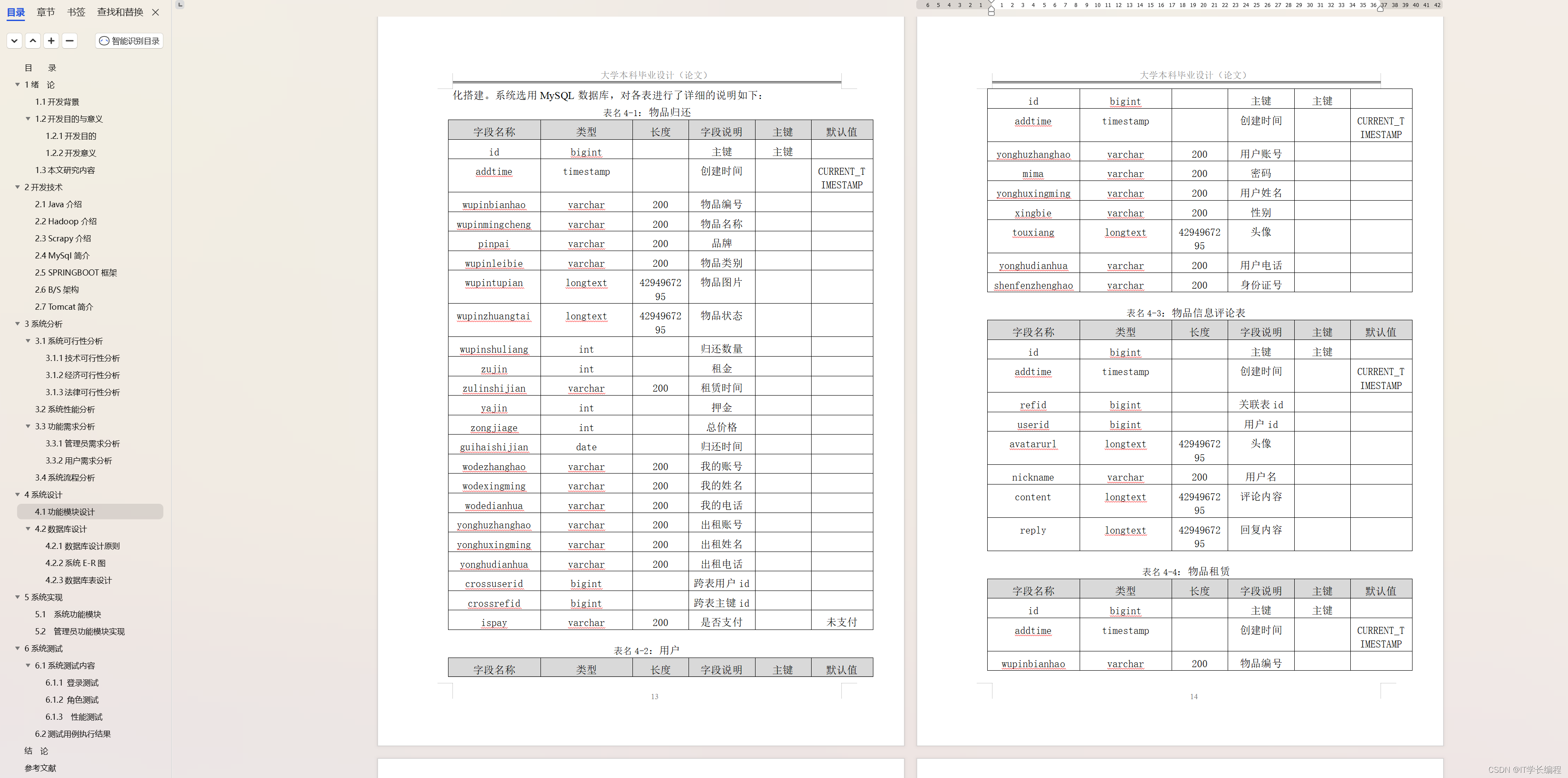
计算机毕业设计 基于Hadoop的物品租赁系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
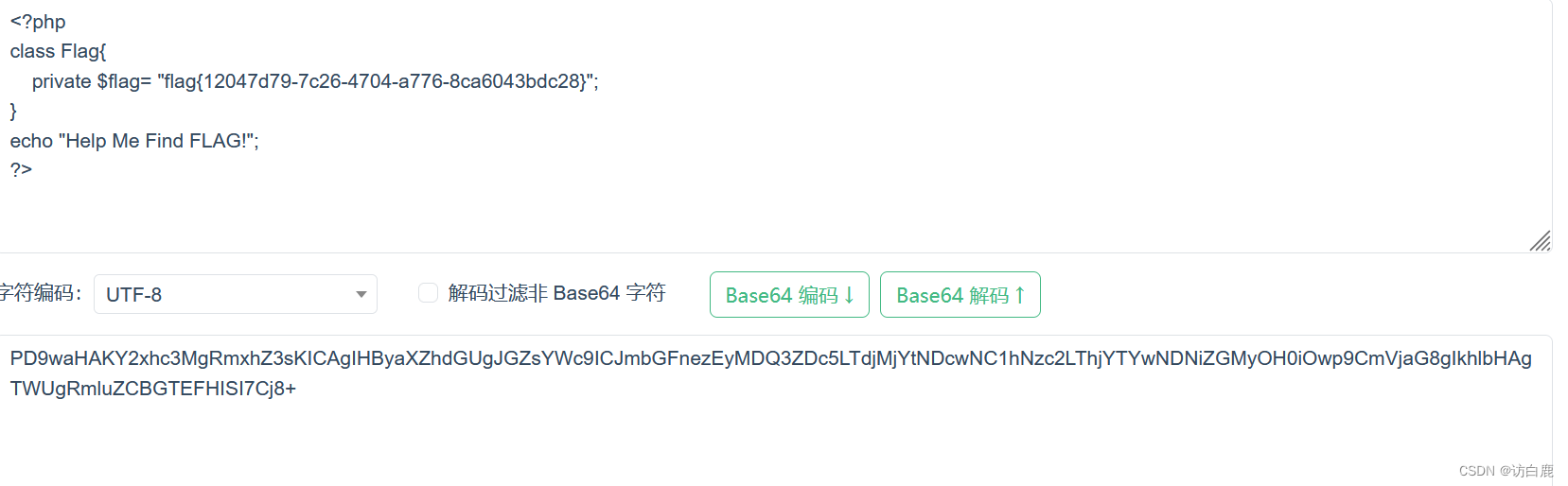
pop链反序列化 [MRCTF2020]Ezpop1
打开题目 网站源码为 Welcome to index.php <?php //flag is in flag.php //WTF IS THIS? //Learn From https://ctf.ieki.xyz/library/php.html#%E5%8F%8D%E5%BA%8F%E5%88%97%E5%8C%96%E9%AD%94%E6%9C%AF%E6%96%B9%E6%B3%95 //And Crack It! class Modifier {protected …...

yolov5从英伟达平台移植到华为昇腾开发板上的思路
作者:朱金灿 来源:clever101的专栏 为什么大多数人学不会人工智能编程?>>> 最近需要将yolov5代码从英伟达平台移植到华为昇腾开发板上。搜了一些代码和资料,大致明白了二者的差别。 1.二者使用的模型文件不一样 yolov…...
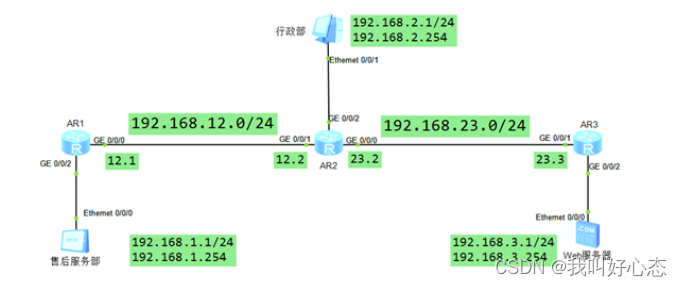
网络运维与网络安全 学习笔记2023.11.25
网络运维与网络安全 学习笔记 第二十六天 今日目标 ACL原理与类型、基本ACL配置、高级ACL配置 高级ACL之ICMP、高级ACL之telnet ACL原理与类型 项目背景 为了企业的业务安全,要求不同部门对服务器有不同的权限 PC1不能访问Server PC2允许访问Server 允许其他所…...

Trustzone/TEE/安全 面试100问
关键词:cache学习、mmu学习、cache资料、mmu资料、arm资料、armv8资料、armv9资料、 trustzone视频、tee视频、ATF视频、secureboot视频、安全启动视频、selinux视频,cache视频、mmu视频,armv8视频、armv9视频、FF-A视频、密码学视频、RME/CCA视频、学习资料下载、免费学习资…...

【数据结构】D : 图的顶点可达闭包
D : 图的顶点可达闭包 Description 给定有向图的邻接矩阵A,其元素定义为:若存在顶点i到顶点j的有向边则A[i,j]1,若没有有向边则A[i,j] 0。试求A的可达闭包矩阵A*,其元素定义为:若存在顶点i到顶点j的有向路径则A*[i,j…...
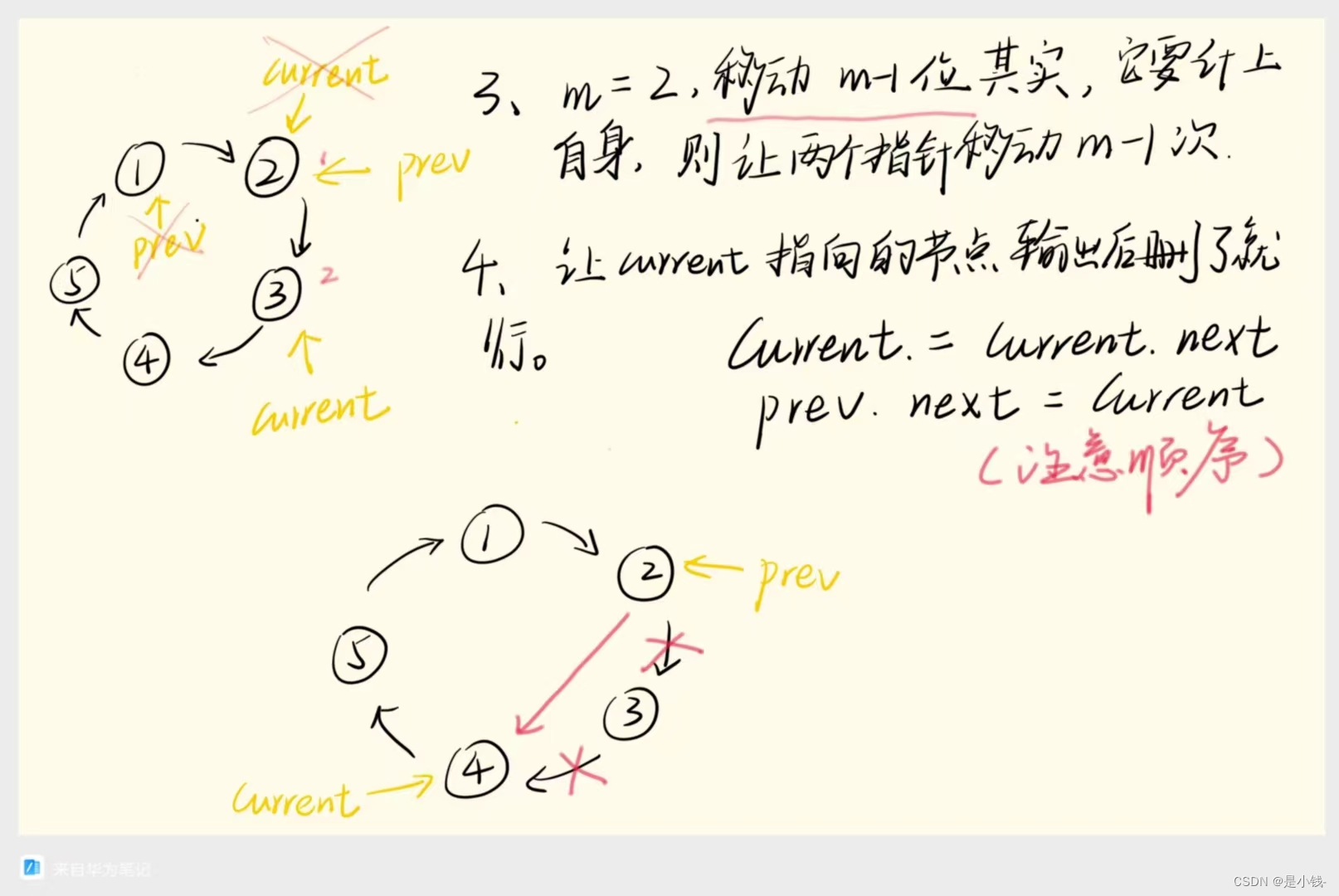
链表?细!详细知识点总结!
链表 定义:链表是一种递归的数据结构,它或者为空(null),或者是指向一个结点(node)的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。 其实链表就是有序的列表,它在内…...
【数据结构实验】排序(三)快速排序算法的改进(三者取中法)
文章目录 1. 引言2. 快速排序算法2.1 传统快速排序2.2 三者取中法 3. 实验内容3.1 实验题目(一)输入要求(二)输出要求 3.2 算法实现 4. 实验结果 1. 引言 快速排序是一种经典的排序算法,其核心思想是通过选择一个基准元…...
【数据结构/C++】栈和队列_顺序栈
#include<iostream> using namespace std; #define MaxSize 10 // 1. 顺序栈 typedef int ElemType; struct Stack {ElemType data[MaxSize];int top; } SqStack; // 初始化栈 void init(Stack &s) {// 初始化栈顶指针s.top -1; } // 入栈 bool push(Stack &s, …...
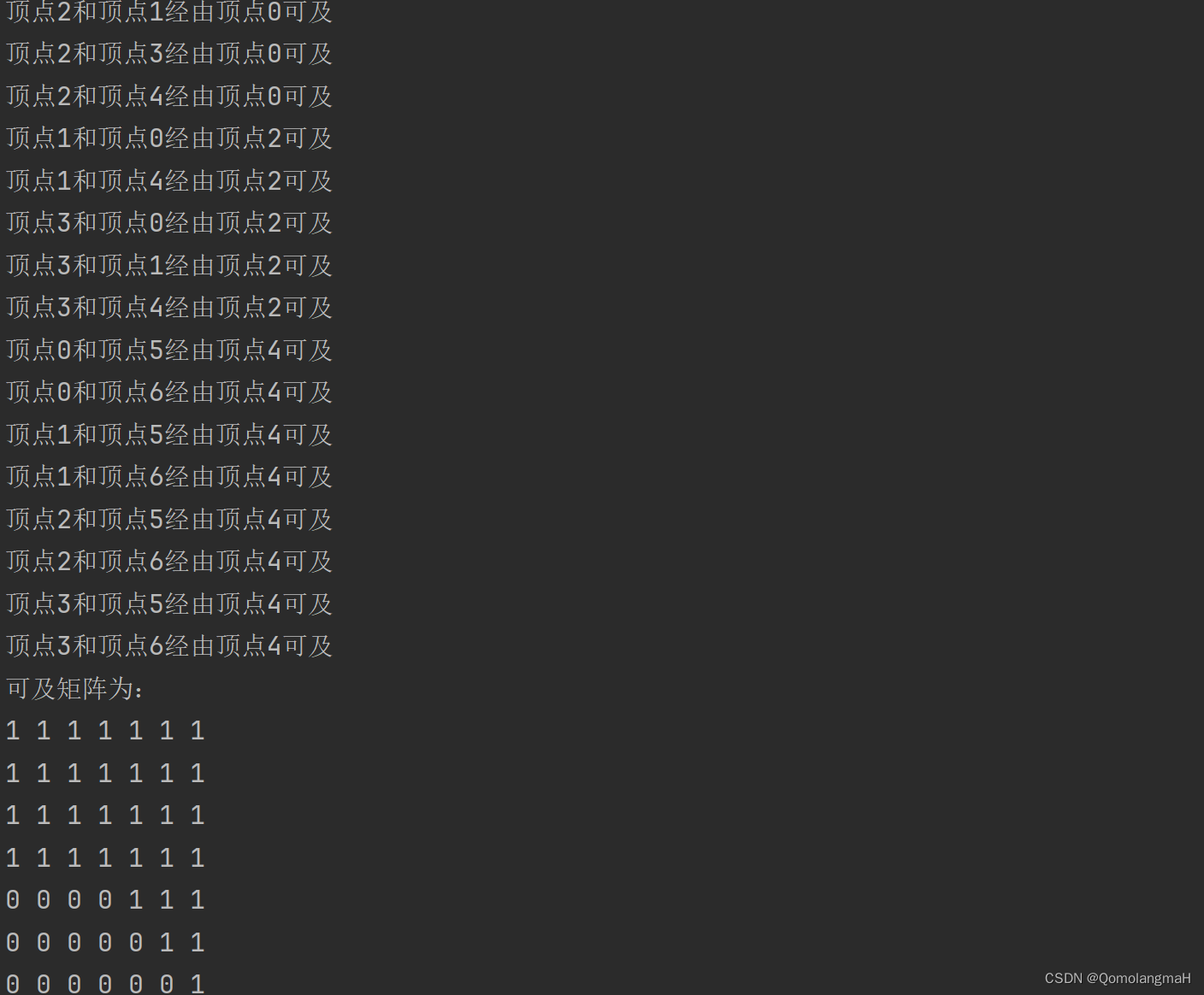
【数据结构实验】图(一)Warshall算法(求解有向图的可达矩阵)
文章目录 1. 引言2. Warshall算法原理2.0 图的基础知识a. 类型b. 表示 2.1 初始化可及矩阵2.2 迭代更新可及矩阵 3. 实验内容3.1 实验题目(一)输入要求(二)输出要求 3.2 算法实现 4. 实验结果 1. 引言 Warshall算法是一种用于求解…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
