比特数据结构与算法(第四章_下)二叉树的遍历
本章将会详细讲解二叉树遍历的四种方式,分别为前序遍历、中序遍历、后续遍历和层序遍历。
在学习遍历之前,会先带大家回顾一下二叉树的基本概念。学习二叉树的基本操作前,
需要先创建一颗二叉树,然后才能学习其相关的基本操作,考虑到我们刚刚接触二叉树,
为了能够先易后难地进行讲解,我们将暂时手动创建一颗简单的二叉树,用来方便大家学习。
等二叉树结构了解的差不多后,后期我们会带大家研究二叉树地真正的创建方式。
1.二叉树概念
复习链接:
比特数据结构与算法(第四章_上)树和二叉树和堆的概念及结构_GR C的博客-CSDN博客
二叉树是什么?① 空树 ② 非空:根节点、根节点的左子树与根节点的又子树组成的。
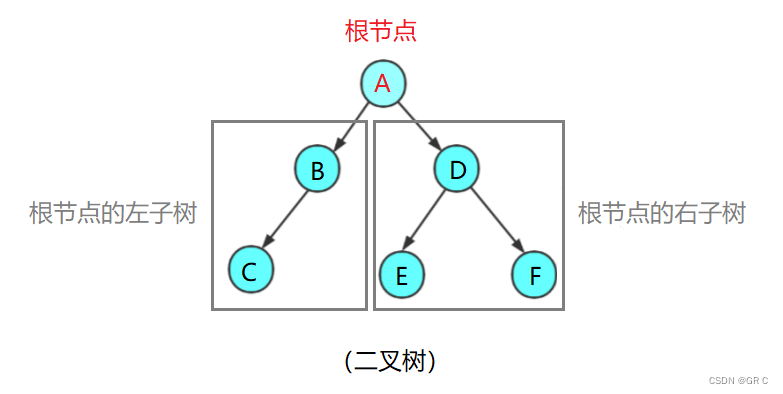
解读:从概念中我们不难看出,二叉树的定义是递归式的。因此后续基本操作中,
我们基本都是按照该概念来实现的!我们可以来看一下,我们不去看 A,我们来看 A 的左子树,
把 B 看作为根节点,又是颗二叉树。
所以,我们可以通过采用递归的手法来实现二叉树。
2.二叉树定义
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>typedef int BTDataType;typedef struct BinaryTreeNode
{struct BinaryTreeNode* left; // 记录左节点struct BinaryTreeNode* right; // 记录右节点BTDataType data; // 存储数据
} BTNode;//创建新节点
BTNode* CreateNode(BTDataType x)
{BTNode* new_node = (BTNode*)malloc(sizeof(BTNode));if (new_node == NULL){printf("malloc failed!\n");exit(-1);}new_node->data = x;new_node->left = new_node->right = NULL;return new_node;
}//手动创建二叉树
BTNode* CreateBinaryTree()
{BTNode* nodeA = CreateNode('A');BTNode* nodeB = CreateNode('B');BTNode* nodeC = CreateNode('C');BTNode* nodeD = CreateNode('D');BTNode* nodeE = CreateNode('E');BTNode* nodeF = CreateNode('F');nodeA->left = nodeB; // AnodeA->right = nodeC; // B CnodeB->left = nodeD; // D E FnodeC->left = nodeE; nodeC->right = nodeF; return nodeA;
}int main(void)
{BTNode* root = CreateBinaryTree();
}3.二叉树深度优先遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历,就是按照某种特定的规则,一次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。 访问节点所做的操作要看具体的应用问题。遍历是二叉树上最重要的运算之一,也是二叉树上进行其他运算的基础。
二叉树遍历(Traversal):沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。 按照规则,二叉树的遍历有:前序 / 中序 / 后序 的递归结构遍历。除了前序、中序和后续遍历外,我们还可以对二叉树进行层序遍历。
比如二叉树的中序遍历:

3.1二叉树前序遍历
前序遍历(Preorder Traversal):访问根节点的操作发生在遍历其右子树之前。
即,首先访问根结点,然后遍历左子树,最后遍历右子树。
代码实现前序遍历:
//二叉树前序遍历
void PreOrder(BTNode* root)
{//首先判断根是否为空,为空就返回if (root == NULL){printf("NULL "); // 暂时打印出来,便于观察 return;}//走到这里说明不为空,根据前序遍历,先访问根节点printf("%c ", root->data);//然后遍历左子树(利用递归)PreOrder(root->left);//最后遍历右子树(利用递归)PreOrder(root->right);// A// B C// D E F 前序:根 左 右//执行输出: A B D NULL NULL NULL C E NULL NULL F NULL NULL
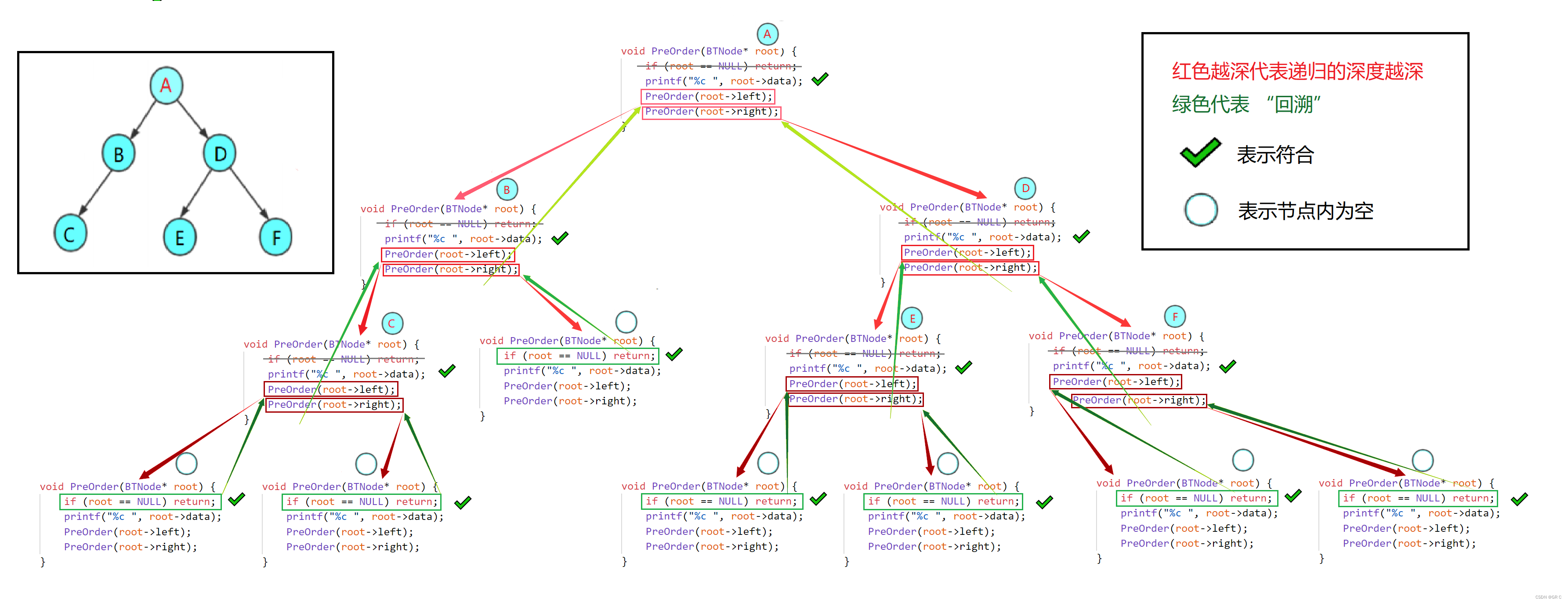
}① 首先判断根是否为空,如果根为空,则返回。这里为了表示,我们把空节点以 " Ø " 打印出来。
② 如果跟不为空,这说明有数据。由于是前序遍历(Preorder),前序遍历是先访问根节点,然后遍历左子树,最后再遍历右子树。所以,我们这里先要访问的是根节点,我们把根节点的数据打印出来。
③ 然后我们需要遍历左子树,这时我们利用递归就可以实现。将根节点 root 的左数 left 传入 PreOrder 函数(将其左树看作根),一直递归下去,直到碰到 root == NULL 则返回。
④ 最后,遍历完左子树后遍历右子树。利用递归,方法同上。
3.2二叉树中序遍历
递归的中序和后序和前序差不多 顺序换一下就行
//二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL) {printf("NULL "); return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);// A// B C// D E F 中序:左 根 右//执行输出:NULL D NULL B NULL A NULL E NULL C NULL F NULL
}3.3二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL) {printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);// A// B C// D E F 后序:左 右 根//执行输出:NULL NULL D NULL B NULL NULL E NULL NULL F C A
}3.4二叉树深度优先遍历完整代码:
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>typedef int BTDataType;typedef struct BinaryTreeNode
{struct BinaryTreeNode* left; // 记录左节点struct BinaryTreeNode* right; // 记录右节点BTDataType data; // 存储数据
} BTNode;//创建新节点
BTNode* CreateNode(BTDataType x)
{BTNode* new_node = (BTNode*)malloc(sizeof(BTNode));if (new_node == NULL){printf("malloc failed!\n");exit(-1);}new_node->data = x;new_node->left = new_node->right = NULL;return new_node;
}//手动创建二叉树
BTNode* CreateBinaryTree()
{BTNode* nodeA = CreateNode('A');BTNode* nodeB = CreateNode('B');BTNode* nodeC = CreateNode('C');BTNode* nodeD = CreateNode('D');BTNode* nodeE = CreateNode('E');BTNode* nodeF = CreateNode('F');nodeA->left = nodeB; // AnodeA->right = nodeC; // B CnodeB->left = nodeD; // D E FnodeC->left = nodeE; nodeC->right = nodeF; return nodeA;
}
//二叉树前序遍历
void PreOrder(BTNode* root)
{//首先判断根是否为空,为空就返回if (root == NULL){printf("NULL "); // 暂时打印出来,便于观察 return;}//走到这里说明不为空,根据前序遍历,先访问根节点printf("%c ", root->data);//然后遍历左子树(利用递归)PreOrder(root->left);//最后遍历右子树(利用递归)PreOrder(root->right);// A// B C// D E F 前序: 根 左 右//执行输出: A B D NULL NULL NULL C E NULL NULL F NULL NULL
}//二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL) {printf("NULL "); return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);// A// B C// D E F 中序:左 根 右//执行输出:NULL D NULL B NULL A NULL E NULL C NULL F NULL
}//二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL) {printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);// A// B C// D E F 后序:左 右 根//执行输出:NULL NULL D NULL B NULL NULL E NULL NULL F C A
}
int main()
{BTNode* root = CreateBinaryTree();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);
}4.二叉树广度优先遍历
4.1层序遍历
层序遍历(Level Traversal):设二叉树的根节点所在的层数为1的情况下,
从二叉树的根节点出发,首先访问第1层的树根节点,然后再从左到右访问第2层上的节点。
接着是第3层的节点……以此类推,自上而下、从左向右地逐层访问树的节点。
该如何实现层序遍历呢? 我们可以利用队列的性质来实现!
我们之前再讲过队列,这里你可以选择自己实现一个队列。
如果不想实现就直接复制即可,因为我们这里重点要学的是层序遍历!
链接:比特数据结构与算法(第三章_下)队列的概念和实现(力扣:225+232+622)_GR C的博客-CSDN博客
本篇完。
下一篇写写二叉树的OJ题,二叉树就暂时结束了
相关文章:

比特数据结构与算法(第四章_下)二叉树的遍历
本章将会详细讲解二叉树遍历的四种方式,分别为前序遍历、中序遍历、后续遍历和层序遍历。在学习遍历之前,会先带大家回顾一下二叉树的基本概念。学习二叉树的基本操作前,需要先创建一颗二叉树,然后才能学习其相关的基本操作&#…...

chatGPT是什么
2022年11月,人工智能公司OpenAI推出了一款聊天机器人:ChatGPT。它能够通过学习和理解人类语言来进行对话,还能与聊天对象进行有逻辑的互动。除了聊天,ChatGPT还能够根据聊天对象提出的要求,进行文字翻译、文案撰写、代…...
jenkins漏洞集合
目录 CVE-2015-8103 反序列化远程代码执行 CVE-2016-0788 Jenkins CI和LTS 远程代码执行漏洞 CVE-2016-0792 低权限用户命令执行 CVE-2016-9299 代码执行 CVE-2017-1000353 Jenkins-CI 远程代码执行 CVE-2018-1000110 用户枚举 CVE-2018-1000861 远程命令执行 CVE-2018…...

用canvas画一个炫酷的粒子动画倒计时
前言 😆 这是一篇踩在活动尾声的文章,主要是之前在摸鱼社群里有人发了个粒子动画的特效视频,想着研究研究写一篇文章出来看看,结果这一下子就研究了半个多月。 😂 下面就把研究成果通过文字的形式展现出来吧…...

Java技术学习——Maven相关知识
一、什么是Maven? Maven是Apache软件基金会组织维护的一款专门为Java项目提供构建和依赖管理支持的工具。 1.1 构建 构建过程包含的主要环节如下: 清理:删除上一次构建的结果,为下一次构建做好准备编译:Java源程序…...

C++ 认识和了解C++
1.在使用C语言写代码的时候开头要用到的是: #include<iostream> using namespace std;不可以写成这样: #include iostream.h(1)iostream是输入输出流类, istream输入流类 cin >> ostream输出流类 cout &…...

u盘误删的文件怎么找回
u盘误删的文件怎么找回?u盘的特点之一就是极其便携,可以容纳各种格式的数据和文件,需要时可以直接使用。每次使用都会或多或少的存放一些文件,但有使用就会有删除,为了不影响使用性,清理存储空间是必要的。清理中如果…...
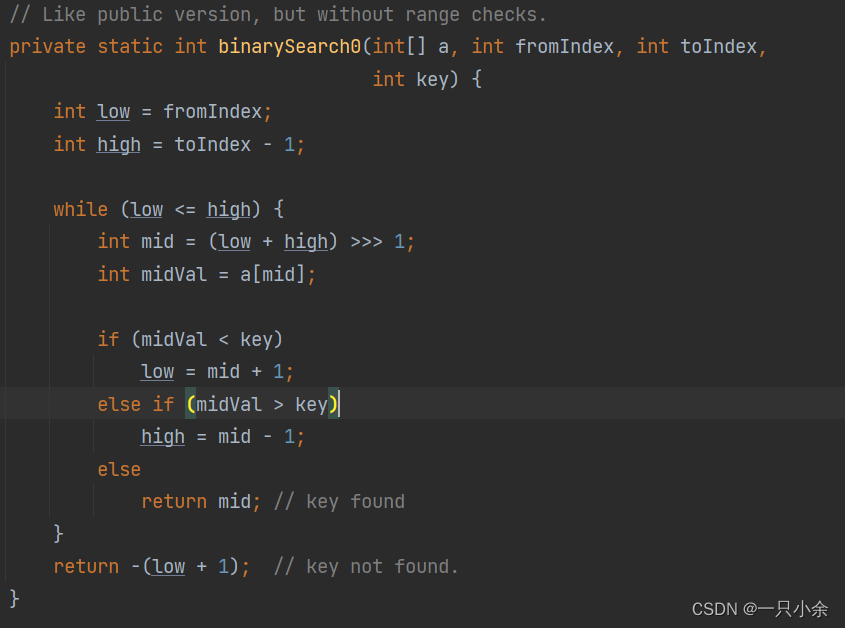
二分查找由浅入深--算法--java
二分查找写在开头算法前提:算法逻辑算法实现简单实现leftright可能超过int表示的最大限度代码分析和变换更多需求:求索引最小的值java二分API应用基础题思考难度方法写在开头 二分查找应该是算比较简单的这种算法了,我本以为还可以。但有时候…...
【学习】笔记本电脑重新安装系统win10
安装系统有很多方法: 软件安装制作启动u盘本文使用的方法就是启动盘安装: 1.首先下载iso镜像文件: msdn我告诉你:MSDN, 我告诉你 - 做一个安静的工具站 (itellyou.cn) 2.下载启动盘制作工具: 制作启动盘rufus:Rufus - 轻松创建 USB 启动盘 3.官网下载: https://do…...
RocketMQ的一些使用理解
1.RocketMQ的生产者生产负载策略(3种) (1)SelectMessageQueueByHash (一致性hash) (2)SelectMessageQueueByMachineRoom (机器随机) (3)SelectMessageQueueByRandom (随机) 第1种一…...

Java枚举详解
一.枚举 1.为什么有枚举? 如果我们的程序需要表示固定的几个值: 比如季节:spring (春),summer(夏),autumn(秋),winter(冬) 用常量表示: public static final int SEASON_SPRING 1;public st…...

虚拟机上安装openKylin详细步骤总结
一、创建虚拟机 首先获取操作系统安装镜像文件: 链接:https://pan.baidu.com/s/1tSuXmDk2ZILR4ieee6iImw?pwdcy47 提取码:cy47 (1-1)进入新虚拟机创建向导,选择“自定义”: (1-…...
)
夜天之书 #74 企业开源的软件协议模型实践(Part 2)
在上一篇文章中,我介绍了企业开源的完全开放源码策略及其风险。完全开放源码,即以符合开源定义的软件协议发布企业自研软件的情形。本文介绍应对完全开放源码后的风险的第一种策略:提高市场占有率与开放标准。与其说是策略,不如说…...

2.webpack实时打包
简介 上一章已经实现了使用 webpack 构建了一个简单的项目;但是我们发现,每次修改了 index.js 需要重新执行 cnpm run dev 命令重新构建 main.js;这在开发阶段是无法忍受的,因为这样调式将浪费大量的时间;还好 webpac…...

KingbaseES V8R3 表加密
前言 透明加密是指将数据库page加密后写入磁盘,当需要读取对应page时进行加密读取。此过程对于用户是透明, 用户无需干预。 该文档进行数据库V8R3版本测试透明加密功能,需要说明,该版本发布时间早于V8R6,所以只能进行表…...

2 为社么软件架构很重要?
2 为社么软件架构很重要? 啊,建造,建造! 这是所有艺术中最崇高的艺术。 — 亨利沃兹沃思朗费罗 如果架构是答案,那么问题是什么? 本章从技术角度重点介绍架构的重要性。我们将研究面包师的十几个最重要…...
Python 之 Pandas merge() 函数、set_index() 函数、drop_duplicates() 函数和 tolist() 函数
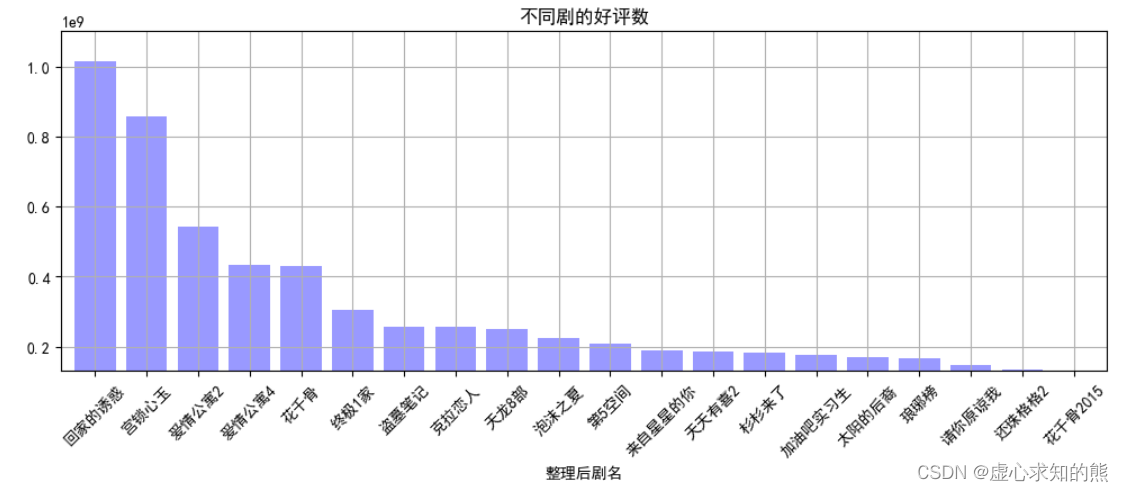
文章目录一、merge() 函数1. inner2. left 和 right3. outer二、set_index() 函数三、drop_duplicates() 函数四、tolist() 函数五、视频数据分析案例1. 问题要求2. 解决过程在最开始,我们先导入常规的 numpy 和 pandas 库。 import numpy as np import pandas as …...
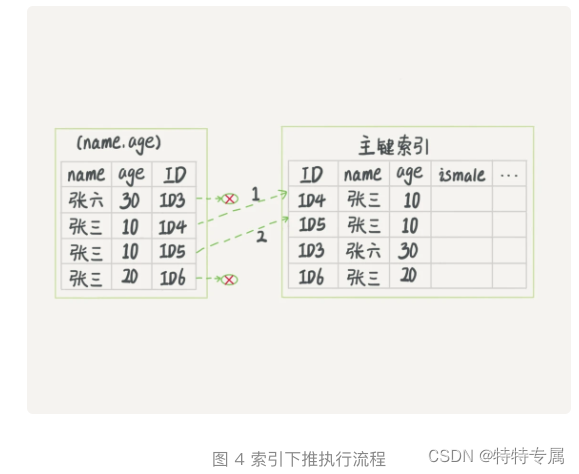
MySQL实战之深入浅出索引(下)
1.前言 在上一篇文章中,我们介绍了InnoDB索引的数据结构模型,今天我们再继续聊一下跟MySQL索引有关的概念。 在介绍之前,我们先看一个问题: 表初始化语句 mysql> create table T ( ID int primary key, k int NOT NULL DEFA…...
leetcode1539. 第 k 个缺失的正整数)
(二分查找)leetcode1539. 第 k 个缺失的正整数
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目 1、题目描述 给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。 请你找到这个数组里第 k 个缺失的正整数。 示例 1: 输入&…...

yaml文件格式详解及实例
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录yaml简介yaml语法规则Yaml语法实例数组…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
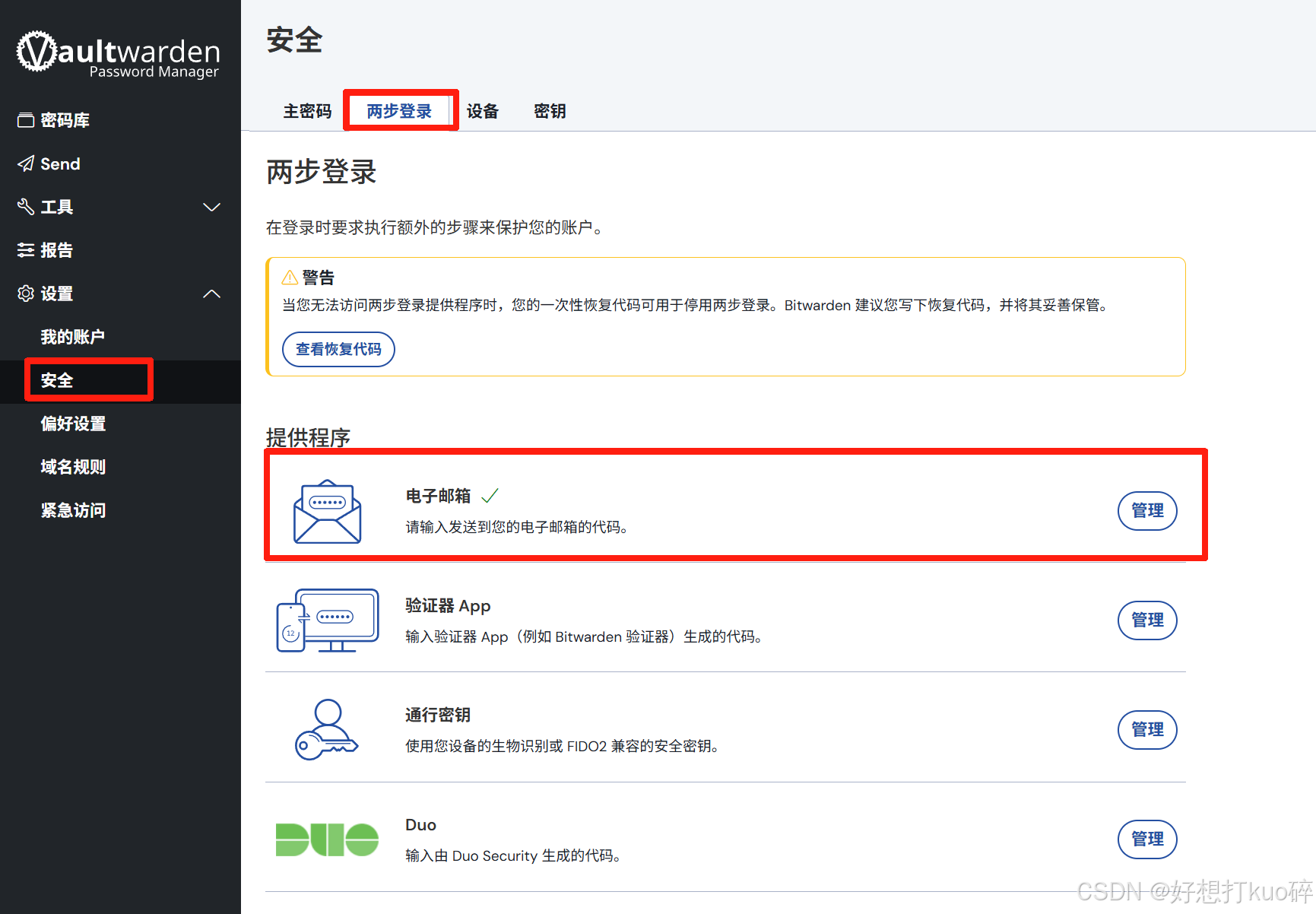
轻量安全的密码管理工具Vaultwarden
一、Vaultwarden概述 Vaultwarden主要作用是提供一个自托管的密码管理器服务。它是Bitwarden密码管理器的第三方轻量版,由国外开发者在Bitwarden的基础上,采用Rust语言重写而成。 (一)Vaultwarden镜像的作用及特点 轻量级与高性…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...
