四边形不等式优化DP
目录
- 四边形不等式内容
- [HNOI2008]玩具装箱
- 解析
- 代码实现
- 参考资料
四边形不等式内容
TODO
[HNOI2008]玩具装箱
解析
- 满足四边形不等式,决策具有单调性. 对于两个位置 i , j i, j i,j, 对应的最优决策点一定有 o p t [ i ] < = o p t [ j ] opt[i] <= opt[j] opt[i]<=opt[j]
- 代码实现
- 需要有一个队列,这里我们使用c++里的双端队列( d e q u e deque deque). 因为需要在队尾插入和弹出,队首弹出的操作.
- 初始化时,队列里只有一个元素, 比如本题中区间 [ 1 , n ] [1, n] [1,n], 决策点为 0 0 0. 这个对所有的位置 [ 1 , n ] [1, n] [1,n]都是合法的一个决策
- 每次插入决策 x x x的时候,从队尾开始判断,如果当前的节点的区间的开始位置决策 x x x更优,就弹出队尾,一直这么做.
- 接上一步, 于是就找到了一个节点(当前队尾): 对应的区间开始位置 x x x不优,结束位置 x x x更优。所以存在一个临界点,我们二分就是要找这么一个位置 p o s pos pos. [ p o s , n ] [pos, n] [pos,n]这部分 x x x更优,其他位置不变.
- 主函数循环部分,我们维持队列的区间都是还未确定最优决策的部分。
- 主函数循环部分,当循环到位置 i i i时候,由于我们已经考虑过小于 i i i的所有决策,因此对于位置 i i i,队首的决策就是位置 i i i的最优决策.
代码实现
#include <bits/stdc++.h>
using namespace std;#ifdef LOCAL
#include "debug.h"
#else
#define debug(...) 42
#endifconst int N = 5e4 + 5;typedef long long LL;int n, L;
// 原数组,以及前缀和
vector<LL> a, sum;
// dp[i]: 前i个玩具的最小费用. dp[i] = min(dp[j] + (s[i] - s[j] + i - j - 1 - L)^2), 0 <= j < i
vector<LL> dp;
// f[i]的最优决策点是谁, 也就是f[i]取得最小值的时候对应的上面的式子中的j. opt[i] = j.
vector<int> op;struct Node {int l, r, c;Node(int _l, int _r, int _c): l(_l), r(_r), c(_c){}
};// 存在插入队尾,弹出队首,弹出队尾三种操作,因此我们使用deque
deque<Node> q;// dp方程: f[j] = f[i] + (x - L) ^ 2
inline LL val(int j, int i) {LL s = sum[i] - sum[j] + i - j - 1 - L;return dp[j] + 1LL * s * s;
}// 用决策x更新
void insert(int x) {// pos表示能更新的那一段的开始位置, 结束位置一定是nint pos = n + 1; // 临界点// 找到x能更新的队列,一定是末尾的一段// 队列里队尾的元素. 看决策x是否是更优的决策. 满足'<='意味着x更优while (q.size() && val(x, q.back().l) <= val(q.back().c, q.back().l)) {pos = q.back().l; // 更新pos: [q,back().l, q.back().r] 这一段肯定x更优q.pop_back();}// 找到了这个区间. 这个区间的右边界x更优,左边界x不优秀. 我们二分寻找临界点在哪里if (q.size() && val(x, q.back().r) <= val(q.back().c, q.back().r)) {int l = q.back().l, r = q.back().r;while (l < r) {int mid = l + r >> 1;if (val(x, mid) <= val(q.back().c, mid)) r = mid; // 对于mid这个点, x的决策更优, 临界点在左边 -> [l, mid]else l = mid + 1; // mid这个点,x不优. 那么临界点在右半部分 -> [mid + 1, r]}// 结束循环时,r是使x成为最优决策的一段的起始位置pos = r;q.back().r = r - 1;}// 说明存在某些位置x的决策比当前队列的优. 也就是进入过上面的代码.if (pos != n + 1) q.push_back(Node(pos, n, x));
}int main() {cin >> n >> L;a = sum = dp = vector<LL>(n + 1, 0);op = vector<int>(n + 1, 0);for (int i = 1; i <= n; i++) cin >> a[i], sum[i] = sum[i - 1] + a[i];q.push_back(Node(1, n, 0)); // 一开始队列只有一个元素,表示[1, n]所有的最优决策点都是0for (int i = 1; i <= n; i++) {// 队头的决策点就是当前i的最优决策int opt = q.front().c;dp[i] = val(opt, i);op[i] = opt;// 弹出已经无用的决策if (q.front().r == i) q.pop_front();q.front().l = i + 1;// 插入当前决策,并用决策i去更新 [i + 1, n]的最优决策insert(i);}cout << dp[n] << endl;return 0;
}
参考资料
- OIWIKI
- 洛谷日报
相关文章:

四边形不等式优化DP
目录 四边形不等式内容[HNOI2008]玩具装箱解析代码实现 参考资料 四边形不等式内容 TODO [HNOI2008]玩具装箱 解析 满足四边形不等式,决策具有单调性. 对于两个位置 i , j i, j i,j, 对应的最优决策点一定有 o p t [ i ] < o p t [ j ] opt[i] < opt[j]…...

Gin 学习笔记01-数据返回
Gin 数据返回 1、返回 string 和 json2、返回 xml 和 ymal3、返回html4、重定向 1、返回 string 和 json c.String()c.JSON() package mainimport ("github.com/gin-gonic/gin""net/http" )func getJSON(c *gin.Context) {//c.String(http.StatusOK, &qu…...
【AI考证笔记】NO.1人工智能的基础概念
目录 一、什么是智能 1.什么是智能 2.智能的种类 二、什么是人工智能 1.人工智能之父——图灵 2.人工智能的定义 三、人工智能的发展阶段 四、哪些工作要被淘汰掉? 以下部分内容来自于百度智能云人才认证培训讲义,腾讯等也有人工智能类似的讲义&…...

【Exception】npm ERR! code UNABLE_TO_GET_ISSUER_CERT_LOCALLY
Talk is cheap, show me the code. 环境 | Environment kversionOSwindows 11nodev18.14.2npm9.5.0 报错日志 | Error log >npm create vitelatest Need to install the following packages:create-vite5.0.0 Ok to proceed? (y) y npm ERR! code UNABLE_TO_GET_ISSUER_…...

持续集成交付CICD:GitLabCI 通过trigger触发流水线
目录 一、理论 1.GitLabCI 二、实验 1.搭建共享库项目 2.GitLabCI 通过trigger触发流水线 三、问题 1.项目app02未触发项目app01 2.GitLab 报502网关错误 一、理论 1.GitLabCI (1) 概念 GitLab CI(Continuous Integration)是一种持续集成工具…...
和wait()方法的区别)
Java 多线程中的sleep()和wait()方法的区别
Java 多线程中的sleep()和wait()方法的区别 1、相同点 sleep()和wait()都可以暂停线程的执行。 2、不同点 所在类不同 sleep()是Thread类的静态方法。 wait()是Object类的方法。 锁释放不同 sleep()是不释放锁的。 wait()是释放锁的。 用途不同 sleep()常用于一定时间内暂停…...

车载以太网-数据链路层-VLAN
文章目录 车载以太网VLAN(Vehicle Ethernet VLAN)车载以太网VLAN帧格式VLAN帧报文VLAN帧报文示例车载以太网VLAN(Vehicle Ethernet VLAN) 车载以太网VLAN(Vehicle Ethernet VLAN)是一种在车辆网络中使用的虚拟局域网技术。它允许在车载以太网网络中创建多个逻辑网络,从…...

【Vue】filter的用法
上一篇: vue的指令 https://blog.csdn.net/m0_67930426/article/details/134599378?spm1001.2014.3001.5502 本篇所使用指令 v-for v-on v-html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"&…...

python web项目导包规范
python web项目导包规范 python 内置的模块通过第三方库安装的模块框架自身提供的模块用户自己定义的模块 如: from __future__ import absolute_import, unicode_literalsfrom debug_toolbar.panels import Panelfrom django.utils.translation import ugettext_…...

AtCoder Beginner Contest 330 题解
目录 A - Counting PassesB - Minimize Abs 1C - Minimize Abs 2D - Counting LsE - Mex and Update A - Counting Passes 原题链接 题目描述 给定N个数和一个整数L,输出大于等于L的数的个数。 public static void solve() throws IOException{int n readInt(), m…...

论文速读《DeepFusion: Lidar-Camera Deep Fusion for Multi-Modal 3D Object Detection》
概括主要内容 文章《DeepFusion: Lidar-Camera Deep Fusion for Multi-Modal 3D Object Detection》提出了两种创新技术,以改善多模态3D检测模型的性能,通过更有效地融合相机和激光雷达传感器数据来提高对象检测的准确性,尤其是在行人检测方面…...
)
关于前端处理后端轮询的操作 (总结)
使用场景:前端首次发起请求获取数据,若失败则每隔1s发起一次知道成功获取数据为止解决方案: 使用轮询操作,涉及定时器的使用和关闭 (使用vue2代码为例) data() {return {pollingResult_en: null, // 处理轮询结果bizI…...
【SpringCloud】设计原则之单一职责与服务拆分
一、设计原则之单一职责 设计原则很重要的一点就是简单,单一职责也就是所谓的专人干专事 一个单元(一个类、函数或微服务)应该有且只有一个职责 无论如何,一个微服务不应该包含多于一个的职责 职责单一的后果之一就是职责单…...

UDP分片和丢包与TCP效果对比
UDP 分片 与 丢包,UDP 真的比 TCP 高效吗? UDP(用户数据报协议)和TCP(传输控制协议)在很多方面都有显著的区别。总体来说,TCP更适合需要可靠传输的应用,例如网页浏览、电子邮件等&a…...
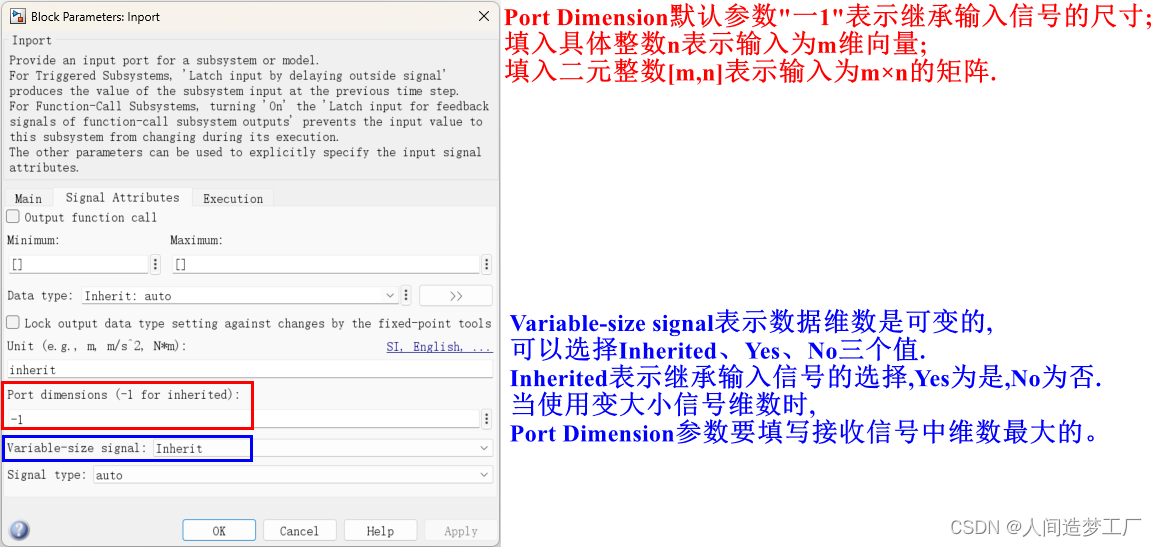
Inport 模块
文章目录 Interpolate datainport 模块存在于模型最顶层Port Dimension 和 Variable-size signal Interpolate data Interpolate data:当将 Workspace 的数据导人模型时, 对没有对应数据点的采样时刻进行线性插值的开关选项。 inport 模块存在于模型最顶层 inpo…...
Deep Learning for Monocular Depth Estimation: A Review.基于深度学习的深度估计
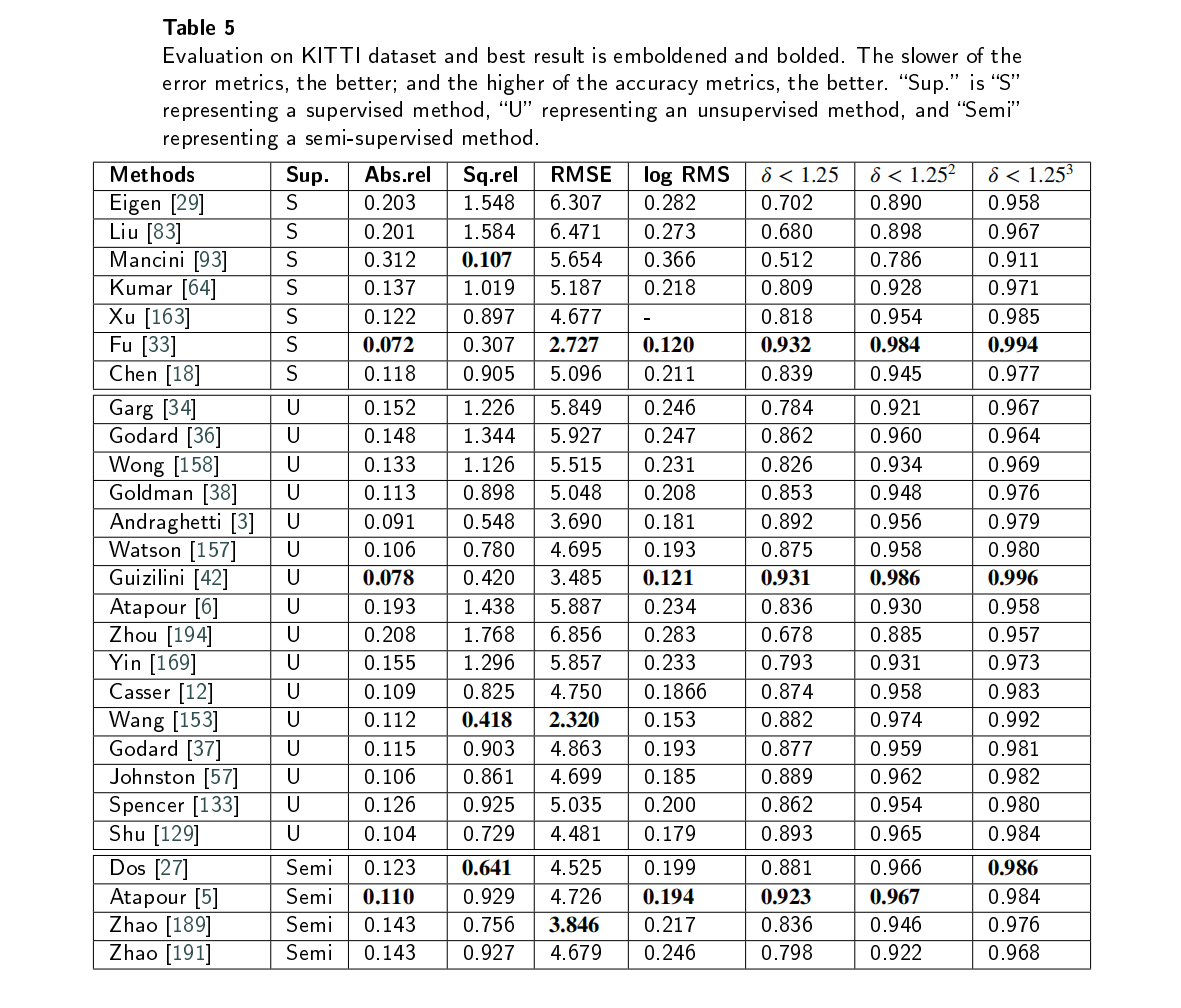
传统的深度估计方法通常是使用双目相机,计算两个2D图像的视差,然后通过立体匹配和三角剖分得到深度图。然而,双目深度估计方法至少需要两个固定的摄像机,当场景的纹理较少或者没有纹理的时候,很难从图像中捕捉足够的特…...
)
点云从入门到精通技术详解100篇-基于深度学习的稀疏点云障碍物检测(续)
目录 3.1 连续帧点云空间特征融合 3.1.1 点云预处理 3.1.2 地面分割 3.1.3 自适应点云聚类...
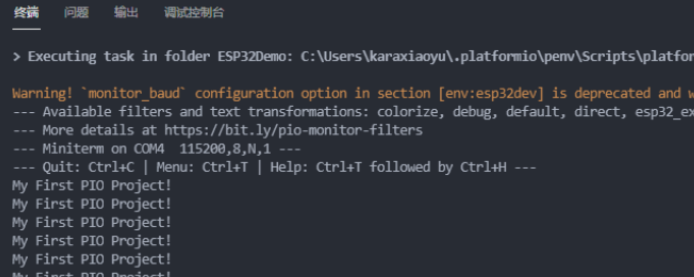
使用VSCode+PlatformIO搭建ESP32开发环境
Arduino IDE本来就是为创客们开发的,虽然没代码提示功能,文件的关系也不清晰,函数不能跳转,头文件也打不开,但人家的初衷就是为了简单而生的;但还是有一些同学喜欢高级点的IDE,也没问题…...

使用flask返回json格式的数据
Flask Flask是一个使用Python编写的轻量级Web框架,它的设计理念是保持简单、灵活和易扩展。它的核心是Werkzeug和Jinja2,并且它本身只提供了非常基础的Web框架功能,例如路由和请求处理等。 使用Flask可以快速创建一个Web应用程序,…...

如何排查java 内存溢出OutOfMemoryError?
当使用Spring Boot进行文件上传时,文件会被读取到内存中进行处理。如果上传的文件较大,会占用大量的内存空间,从而导致内存溢出(OutOfMemory)问题。以下是一些建议的排查方案: 调整 JVM 内存设置ÿ…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
