LeetCode算法题解(动态规划,背包问题)|LeetCode1049. 最后一块石头的重量 II、LeetCode494. 目标和
一、LeetCode1049. 最后一块石头的重量 II
题目链接:1049. 最后一块石头的重量 II
题目描述:
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40] 输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
算法分析:
定义dp数组及下标含义:
dp[j]:表示容量为j的背包所能装的物品最大价值(石头的重量)为dp[j]。
递推公式:
dp[j]=max(dp[j],dp[j-stones[i]]+stones[i])。
初始化:
dp[0]=0。
遍历顺序:
先遍历物品在遍历背包容量。
代码如下:
class Solution {public int lastStoneWeightII(int[] stones) {int len = stones.length;int sum = 0;for(int i = 0; i < len; i++)sum += stones[i];int mid;mid = sum / 2;int[] dp = new int[mid + 1];for(int i = stones[0]; i <= mid; i++)dp[i] = stones[0];for(int i = 1; i < len; i++) {for(int j = mid; j >= stones[i]; j--) {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - dp[mid] * 2;}
}二、LeetCode494. 目标和
题目链接:494. 目标和
题目描述:
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
算法分析:
设添加+的元素集合总和为add,添加-的元素集合总和为des,则原数组的所有元素之和sum=add+des
由题意target=add-des;
des=add-target;
sum=add+(add-target);
add=(sum+target)/2;
所以我们只需要在原数组中找出和等于add的方法数就可以了。
于是我们可以用动态规划中背包思路来解。
定义dp数组及下标含义:
dp[j]表示元素和为j的方法有dp[j]种。
递推公式:
dp[j]+=dp[j-nums[i]];
例如:若有元素1,2,3,4,5,6,则加上该元素后和为5的方法有dp[5]=dp[5-1]+dp[5-2]+dp[5-3]+dp[5-4]+dp[5-5]种(j>=nums[i])。
初始化:
我们初始化dp[0]=1;
表示元素和为0的方法有一种,因为如果为0的话那么所有的递推结果都将为0。
遍历顺序:
先遍历元素在遍历总和。
代码如下:
class Solution {public int findTargetSumWays(int[] nums, int target) {int len = nums.length;int sum = 0;//数组总和for(int i = 0; i < len; i++)sum += nums[i];if(Math.abs(target) > sum) return 0;//如果target的绝对值大于sum,那么无论数组中所有元素都取正还是负都不肯能等于targetif((sum + target) % 2 != 0) return 0;//没有结果,如sum是5target是0的话,无解int add = (sum + target) / 2;int[] dp = new int[add + 1];dp[0] = 1;for(int i = 0; i < len; i++) {for(int j = add; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[add];}
}总结
求背包问题时要明确定义dp数组所表示的含义,对于不同的问题可能会有不同的定义,
如1049. 最后一块石头的重量 II中,dp[j]表示容量为j的背包所能装的石头的重量最大为dp[j]。
而494. 目标和中dp[j]表示装满容量为j的方法有dp[j]种。
相关文章:
|LeetCode1049. 最后一块石头的重量 II、LeetCode494. 目标和)
LeetCode算法题解(动态规划,背包问题)|LeetCode1049. 最后一块石头的重量 II、LeetCode494. 目标和
一、LeetCode1049. 最后一块石头的重量 II 题目链接:1049. 最后一块石头的重量 II 题目描述: 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将…...

使用Pytorch从零开始构建LSTM
长短期记忆(LSTM)网络已被广泛用于解决各种顺序任务。让我们了解这些网络如何工作以及如何实施它们。 就像我们一样,循环神经网络(RNN)也可能很健忘。这种与短期记忆的斗争导致 RNN 在大多数任务中失去有效性。不过&a…...
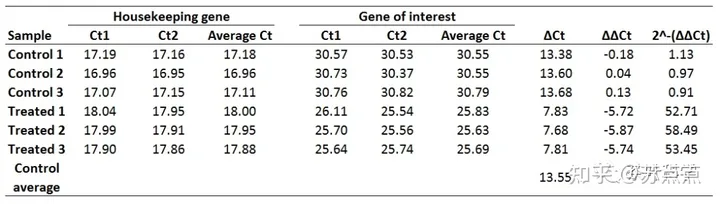
qRT-PCR相对定量计算详解qPCR相对定量计算方式——2^-(∆∆Ct) deta t
做完转录组分析之后,一般都要求做qRT-PCR来验证二代测序得到的转录本表达是否可靠。荧光定量PCR是一种相对表达定量的方法,他的计算方法有很多,常用的相对定量数据分析方法有双标曲线法,ΔCt法,2^-ΔΔCt法(Livak法)&a…...

BART non-Cartesian 重建:并行成像 压缩感知
本文主要使用并行成像和压缩感知方法实现non-Cartesian MRI 数据的重建。 目录 1 自定义MRI kspace trajectory 2 自定义该 trajectory下的多通道MRI数据 3 使用NUFFT 直接做欠采样数据的重建...

UDP客户端使用connect与UDP服务器使用send函数和recv函数收发数据
服务器代码编译运行 服务器udpconnectToServer.c的代码如下: #include<stdio.h> #include<stdlib.h> #include<string.h> #include<unistd.h> #include<arpa/inet.h> #include<sys/socket.h> #include<errno.h> #inclu…...
闭环检测器)
SLAM ORB-SLAM2(9)闭环检测器
SLAM ORB-SLAM2(9)闭环检测器 1. LoopClosing2. 成员变量2.1. 系统成员变量2.2. 关键帧2.3. 共视关系2.4. 闭环检测2.5. 全局 BA(光束法平差)2.6. 其他操作3. 成员函数3.1. 构造函数3.2. 主要函数3.3. 更新操作3.4. 标识设置和查询接口1. LoopClosing 在《SLAM ORB-SLAM2(…...
(二))
目标检测YOLO系列从入门到精通技术详解100篇-【目标检测】SLAM(基础篇)(二)
目录 知识储备 概率论基础 边缘概率 联合概率和独立 独立与条件独立...

TikTok 将开源“云中和”边缘加速器
“从某种意义上说,我们正在努力破解云的骨干网,以造福于我们,”TikTok产品管理基础设施经理Vikram Siwach指出,他解释了该公司即将开源的“全球服务加速器”的好处,这是一个可编程的边缘平台,可将应用程序需…...
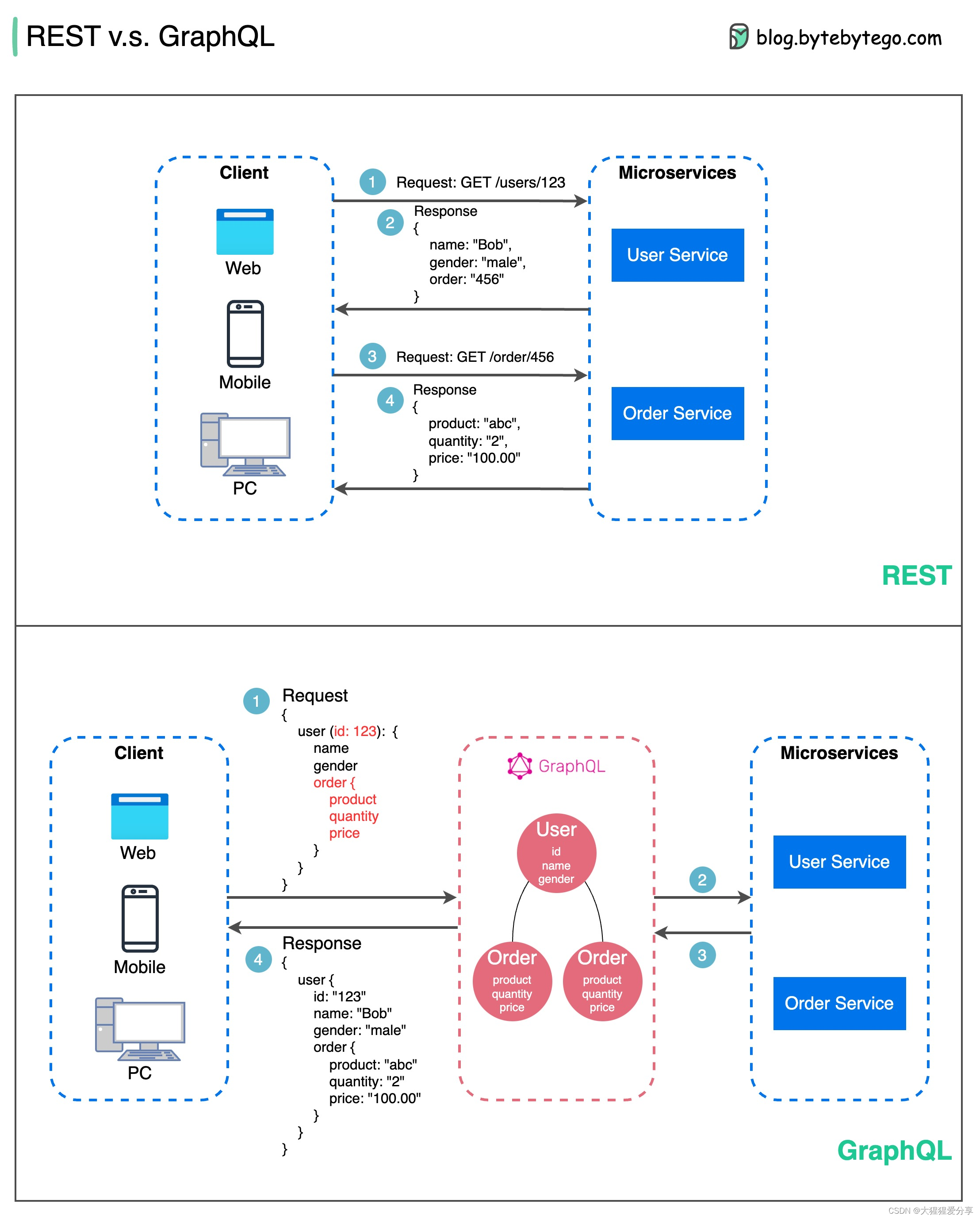
【通讯协议】REST API vs GraphQL
在API设计方面,REST和GraphQL各有缺点。下图显示了 REST 和 GraphQL 之间的快速比较。 REST 使用标准 HTTP 方法(如 GET、POST、PUT、DELETE)进行 CRUD 操作。当您需要在单独的服务/应用程序之间提供简单、统一的接口时,效果很好…...

Linux在安装epel-release时,报错epel-release-7-14.noarch.rpm 的公钥尚未安装
Linux在安装epel-release时报错: [rootXWDBDEV01 ~]# yum install epel-release 已加载插件:fastestmirror, langpacks, product-id, search-disabled-repos, subscription-managerThis system is not registered with an entitlement server. You can …...

在 STM32 上实现温度补偿和校正
本文介绍了如何在 STM32 微控制器上实现温度补偿和校正,以提高温度传感器的测量精度。首先,我们将简要介绍温度补偿和校正的原理和目的。然后,我们将详细讨论在 STM32 上实现温度补偿和校正的步骤和方法。同时,提供了一个简单的示…...
PasteNow for mac剪贴板工具
PasteNow 是一款简单易用的剪贴板管理工具,可帮助用户快速存储和管理剪贴板上的文本和图片内容。用户可以使用 PasteNow 软件快速将文本内容保存到不同的笔记或页面中,也可以方便地将剪贴板上的图片保存到本地或分享给其他应用程序。 此外,P…...

Spark---补充算子
一、Spark补充Transformation算子 1、join,leftOuterJoin,rightOuterJoin,fullOuterJoin 作用在K,V格式的RDD上。根据K进行连接,对(K,V)join(K,W)返回(K,&a…...

第一百八十回 介绍两种阴影效果
文章目录 1. 概念介绍2. 实现方法3. 代码与效果3.1 示例代码3.2 运行效果 4. 内容总结 我们在上一章回中介绍了"自定义SlideImageSwitch组件"相关的内容,本章回中将介绍两种阴影效果.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在…...
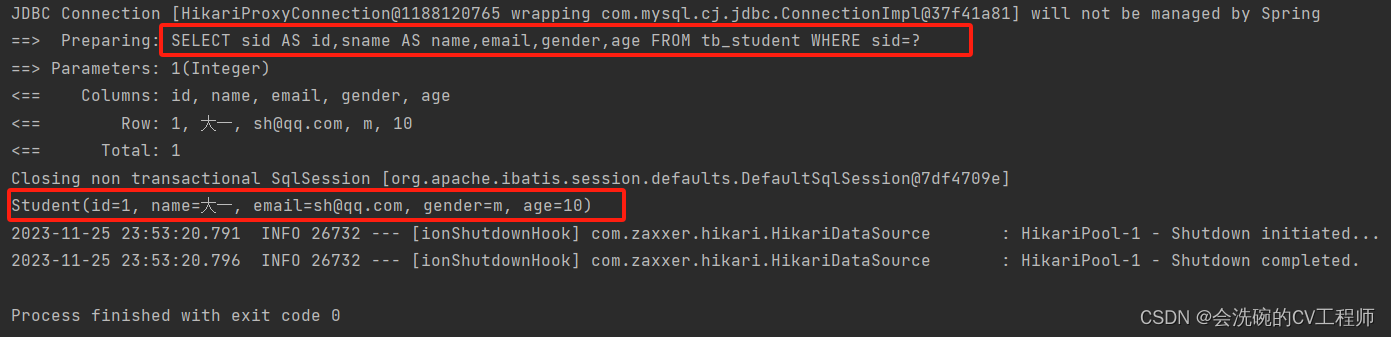
MyBatisPlus入门介绍
目录 一、MyBatisPlus介绍 润物无声 效率至上 丰富功能 二、Spring集成MyBatisPlus 三、SpringBoot集成MyBatisPlus 一、MyBatisPlus介绍 MyBatis-Plus(简称 MP)是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,…...

详解分布式微服务架构
目录 一、微服务简介 1、分布式微服务架的诞生 2、微服务架构与SOA架构的区别 3、微服务框架引来的问题 二、服务通信 RESTful API: 消息队列(如RabbitMQ、Kafka): gRPC: GraphQL: Service Mesh&…...
Navicat 技术指引 | 适用于 GaussDB 的用户权限设置
Navicat Premium(16.2.8 Windows版或以上) 已支持对 GaussDB 主备版的管理和开发功能。它不仅具备轻松、便捷的可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结构同步、协同合作、数据迁移等),这…...

究极短的快排代码【QuickSort】
快排 QuickSort 两边向中间扫描法:取一个基点值,从左往右扫描,基点值左边所有元素小于它,遇到大于基点值的则停下,开始从右往左扫描,右边所有元素大于他,遇到小于基点值则停下,如果…...
MUYUCMS v2.1:一款开源、轻量级的内容管理系统
MuYuCMS:一款基于Thinkphp开发的轻量级开源内容管理系统,为企业、个人站长提供快速建站解决方案。它具有以下的环境要求: 支持系统:Windows/Linux/Mac WEB服务器:Apache/Nginx/ISS PHP版本:php > 5.6 (…...

⑩【Redis Java客户端】:Jedis、SpringDataRedis、StringRedisTemplate
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ Jedis、SpringDataRedis、StringRedisTemplate…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
