求集合的笛卡尔乘积
求集合的笛卡尔乘积
- 一:【实验目的】
- 二:【实验内容】
- 三:【实验原理】
- 四:代码实现:
一:【实验目的】
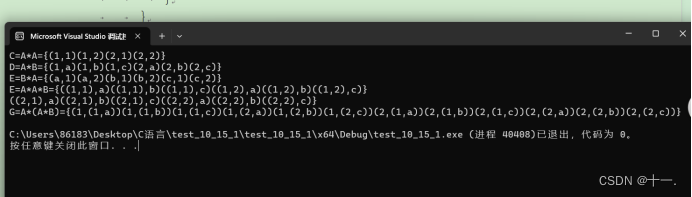
通过编实现给定集合A和B的笛卡尔积C=AA,D=AB,E=BA,F=AAB,G=A(A*B).
二:【实验内容】
已知所给集合A={1,2},B={a,b,c},求A,B的笛卡尔积C=AA,D=AB,E=BA,F=AAB,G=A(A*B)
三:【实验原理】
笛卡尔乘积是以有序偶为元素的集合,它的定义为C={(x,y)|x∈A,y∈B}。所以欲求笛卡尔积,只需取尽集合A的元素和集合B的元素,并构成序偶(a,b)送入C中即可。
四:代码实现:
#include <stdio.h>
int main()
{char A[] = {'1','2'};int M = sizeof(A)/sizeof(A[0]);char B[] = { 'a','b','c' };int N = sizeof(B) / sizeof(B[0]);char C[2][2] = { 0 };//求C的笛卡尔积,C=A*Aprintf("C=A*A=");printf("{");int i = 0;int j = 0;for (i = 0; i < M; i++){for (j = 0; j < M; j++){C[i][0] = A[i];C[i][1] = A[j];printf("(%c,%c)", C[i][0], C[i][1]);}}printf("}");printf("\n");//求D的笛卡尔积,D=A*Bchar D[2][3] = { 0 };printf("D=A*B=");printf("{");for (i = 0; i < M; i++){for (j = 0; j < N; j++){D[i][0] = A[i];D[i][1] = B[j];printf("(%c,%c)", D[i][0], D[i][1]);}}printf("}");printf("\n");//求E的笛卡尔积,E=B*Achar E[3][2] = { 0 };printf("E=B*A=");printf("{");for (i = 0; i < N; i++){for (j = 0; j < M; j++){E[i][0] = B[i];E[i][1] = A[j];printf("(%c,%c)", E[i][0], E[i][1]);}}printf("}");printf("\n");//求F的笛卡尔积,E=A*A*Bchar F[2][2][3] = { 0 };printf("E=A*A*B=");printf("{");for (i = 0; i < M; i++){for (j = 0; j < M; j++){for (int k = 0; k < N; k++){F[i][j][0] = A[i];F[i][j][1] = A[j];F[i][j][2] = B[k];printf("((%c,%c),%c)", F[i][j][0], F[i][j][1], F[i][j][2]);}}printf("}");printf("\n");}//求G的笛卡尔积,G=A*(A*B)char G[2][2][3] = { 0 }; printf("G=A*(A*B)=");printf("{");for (i = 0; i < M; i++){for (j = 0; j < M; j++){for (int k = 0; k < N; k++){G[i][j][0] = A[i];G[i][j][1] = A[j];G[i][j][2] = B[k];printf("(%c,(%c,%c))", G[i][j][0], G[i][j][1], G[i][j][2]);}}}printf("}");return 0;
}
【实验心得】
通过这个实验,我们可以更深入的了解集合的性质和它们之间的相互作用。在这个实验中,我们将两个集合的元素进行组合,形成了一个新的集合。更深入地了解集合之间的关系,同时这个实验也有助于培养我们的逻辑思维能力和分析问题的能力。
相关文章:

求集合的笛卡尔乘积
求集合的笛卡尔乘积 一:【实验目的】二:【实验内容】三:【实验原理】四:代码实现: 一:【实验目的】 通过编实现给定集合A和B的笛卡尔积CAA,DAB,EBA,FAAB,GA(A*B). 二:【实验内容】…...

Linux系统常用指令大全(图文详解)
目录 前言 一、UNIX的登录与退出 1、登录 (1)执行格式: (2)步骤 2、退出 二、UNIX命令格式 三、常用命令 1、目录操作 (1)显示目录文件 ls (2)建新目录 …...

基于PLC触摸屏控制的伺服电机绕线机
摘 要 绕线机是专供连续绕制多圈电位器绕阻的专用机床设备。本文介绍了采用 PLC作为主控制机器,触摸屏作为操作界面,步进电机、伺服电机驱动的绕线机系统。描述 了触摸屏的原理、分类和触摸屏人机界面的控制方式,完成了触摸屏人机界面设计。…...

1.8 C语言之参数传递
1.8 C语言之参数传递 一、参数传递 一、参数传递 在C语言中,所有的参数传递都是值传递,也就是说,传递给被调用函数的参数值存放在临时变量中,而不是存放在原来的变量中。这与其他语言的引用传递有所不同。在C语言中,被…...
【Linux】进程间通信——system V共享内存、共享内存的概念、共享内存函数、system V消息队列、信号量
文章目录 进程间通信1.system V共享内存1.1共享内存原理1.2共享内存数据结构1.3共享内存函数 2.system V消息队列2.1消息队列原理 3.system V信号量3.1信号量原理3.2进程互斥 4.共享内存的使用示例 进程间通信 1.system V共享内存 1.1共享内存原理 共享内存区是最快的IPC形式…...
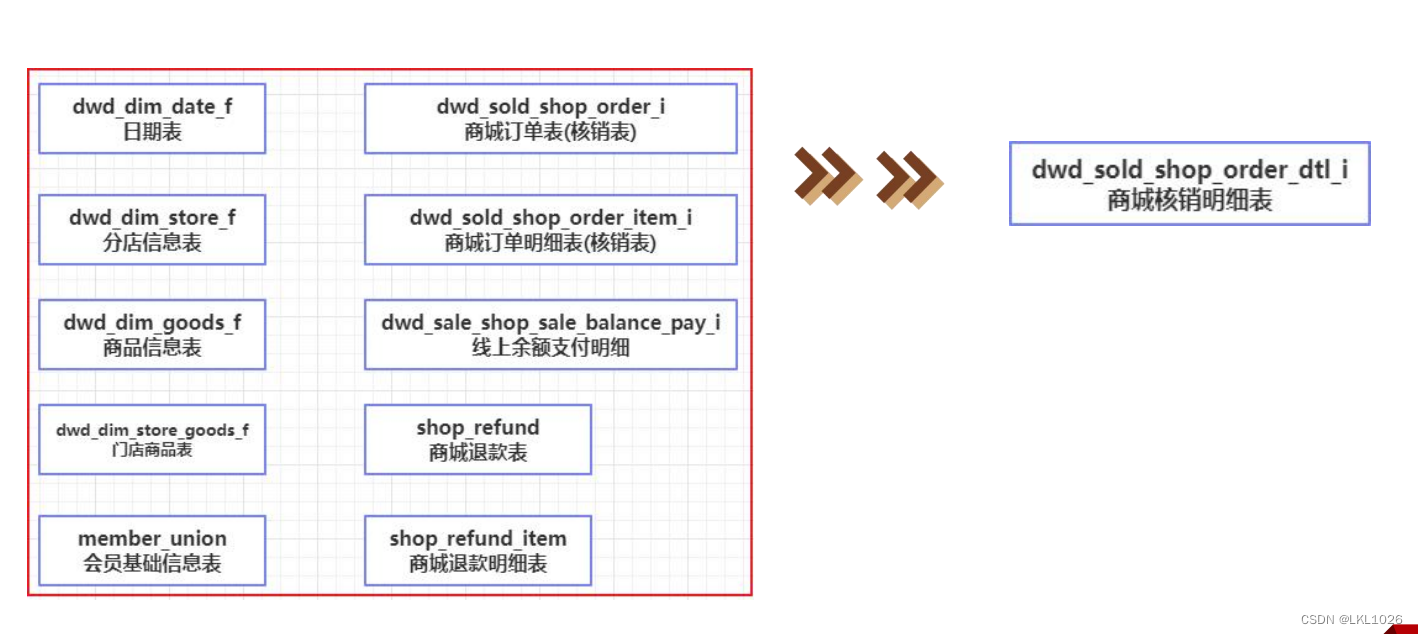
【黑马甄选离线数仓day05_核销主题域开发】
1. 指标分类 通过沟通调研,把需求进行分析、抽象和总结,整理成指标列表。指标有原子指标、派生指标、 衍生指标三种类型。 原子指标基于某一业务过程的度量值,是业务定义中不可再拆解的指标,原子指标的核心功能就是对指标…...

使用gin 代理 web网页
问web项目的代理,业界常用的方案是nginx做代理,这个是网上最多资料的。 因为我需要做自己的流量转发,也就是所有访问都要经过我的一个流量分发微服务,这和nginx作用冲突了。如果再加个nginx来做第一层方向代理和网页的静态资源代…...
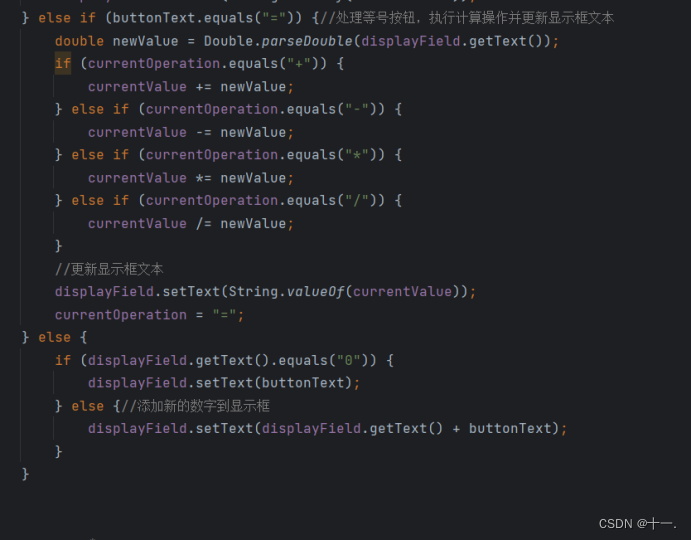
计算器的模拟实现
计算器的模拟实现 一、实验题目:计算器二:实验目的:三:实验内容与实现1:【实验内容】2:【实验实现】1.计算器界面的实现,如下图所示:2:各项功能的实现,如下图…...

CentOS7搭建smb服务器
安装smb sudo yum install samba samba-client samba-common配置smb vim /etc/samba/smb.conf [shared] path /path/to/shared/folder writable yes browsable yes guest ok yes valid users yourname添加smb用户 sudo useradd youname sudo smbpasswd -a youname然后会…...
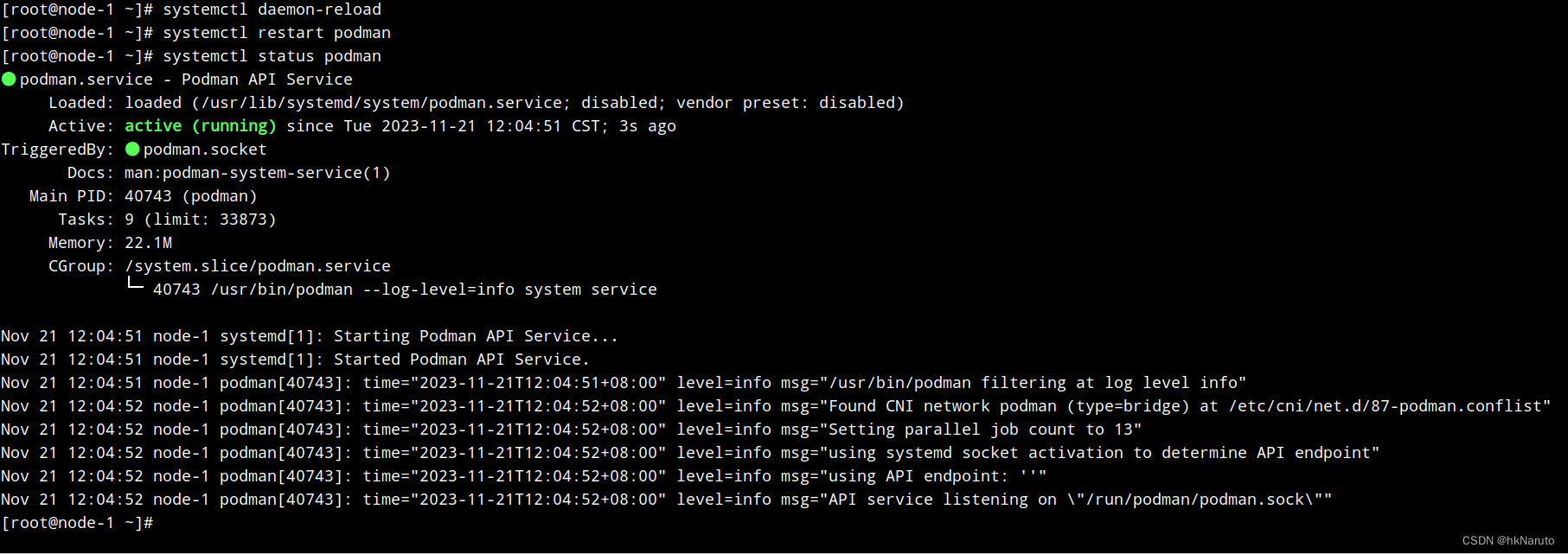
openEuler 22.03 LTS x86_64 cephadm 部署ceph 16.2.14 未完成 笔记
环境 准备三台虚拟机 10.47.76.94 node-1 10.47.76.95 node-2 10.47.76.96 node-3 下载cephadm [rootnode-1 ~]# yum install cephadm Last metadata expiration check: 0:11:31 ago on Tue 21 Nov 2023 10:00:20 AM CST. Dependencies resolved. Package …...

Java计算时间差,距结束还有几天几小时几分钟
文章目录 1、写法2、备份3、LocalDate、LocalDateTime、Date、String互转 1、写法 //静态方法,传入年月日时分秒 LocalDateTime startTime LocalDateTime.of(2023, 11, 22, 15, 09, 59); LocalDateTime endTime LocalDateTime.of(2023, 11, 30, 0, 0, 0); //计算…...

【云原生 Prometheus篇】Prometheus的动态服务发现机制与认证配置
目录 一、Prometheus服务发现的方式1.1 基于文件的服务发现1.2 基于consul的服务发现1.3 基于 Kubernetes API 的服务发现1.3.1 简介1.3.2 基于Kurbernetes发现机制的部分配置参数 二、实例一:部署基于文件的服务发现2.1 创建用于服务发现的文件2.2 修改Prometheus的…...
ref详解(C#)
本质上来说 ref 的就是把 C/C 指针的那一套又拿回来了,而且还封装成一套自己的玩法。 我想设计者的初心把 ref 的功能限制得死死的,可能也考虑到 C# 是一门面向业务开发的语言,讲究的是做项目快狠准,性能反而不是第一要素&#x…...

运维高级-day01
shell回顾 1、快速生成版权控制信息,具体的内容自己替换 [root scripts]# cat ~/.vimrc autocmd BufNewFile *.py,*.cc,*.sh,*.java exec ":call SetTitle()" func SetTitle() if expand("%:e") sh call setline(1,"#!/bin/bash")…...
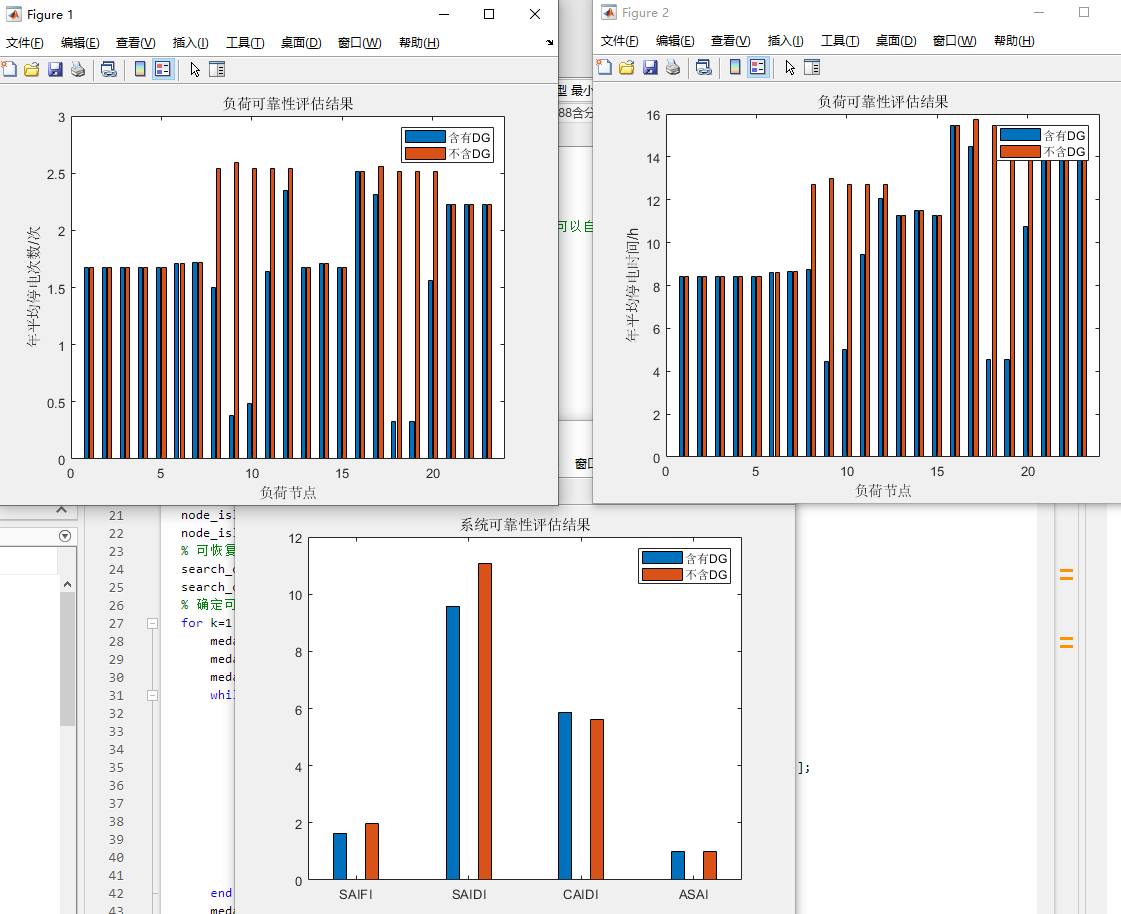
含分布式电源的配电网可靠性评估matlab程序
微❤关注“电气仔推送”获得资料(专享优惠) 参考文献: 基于仿射最小路法的含分布式电源配电网可靠性分析——熊小萍 主要内容: 通过概率模型和时序模型分别进行建模,实现基于概率模型最小路法的含分布式电源配电网…...

k8s docker总结特殊点
k8s docker总结特殊点 前言一、docker 的驱动。1、cgroup:(Control Groups)2、日志驱动(log driver)3、存储驱动4、网络驱动: 二、k8s中网络插件(常用calico,次flannel)**Flannel:**…...

区块链技术与应用 【全国职业院校技能大赛国赛题目解析】第四套区块链应用后端开发
第四套区块链应用后端开发 环境 : ubuntu20 fisco : 2.8.0 springboot 2.1.1 fisco-java-sdk: 2.7.2 maven 3.8.8 前言 这套后端样题,只涉及调用fisco的系统接口,不涉及此食品溯源项目的业务接口,所以我就直接生成一个springboot项目进行完成此题目。 请提前准备好一…...

《向量数据库指南》——向量数据库Milvus Cloud搭建Excel公式编辑器助手
引言 在日常工作中,Excel是我们经常使用的办公工具,而熟练应用Excel公式对于提高工作效率非常重要。然而,有时候我们会遇到一些复杂的需求,需要用到较为专业的Excel公式,而这正是Excel公式编辑器助手的用武之地。本文将介绍如何利用向量数据库Milvus Cloud搭建GPT大模型和…...
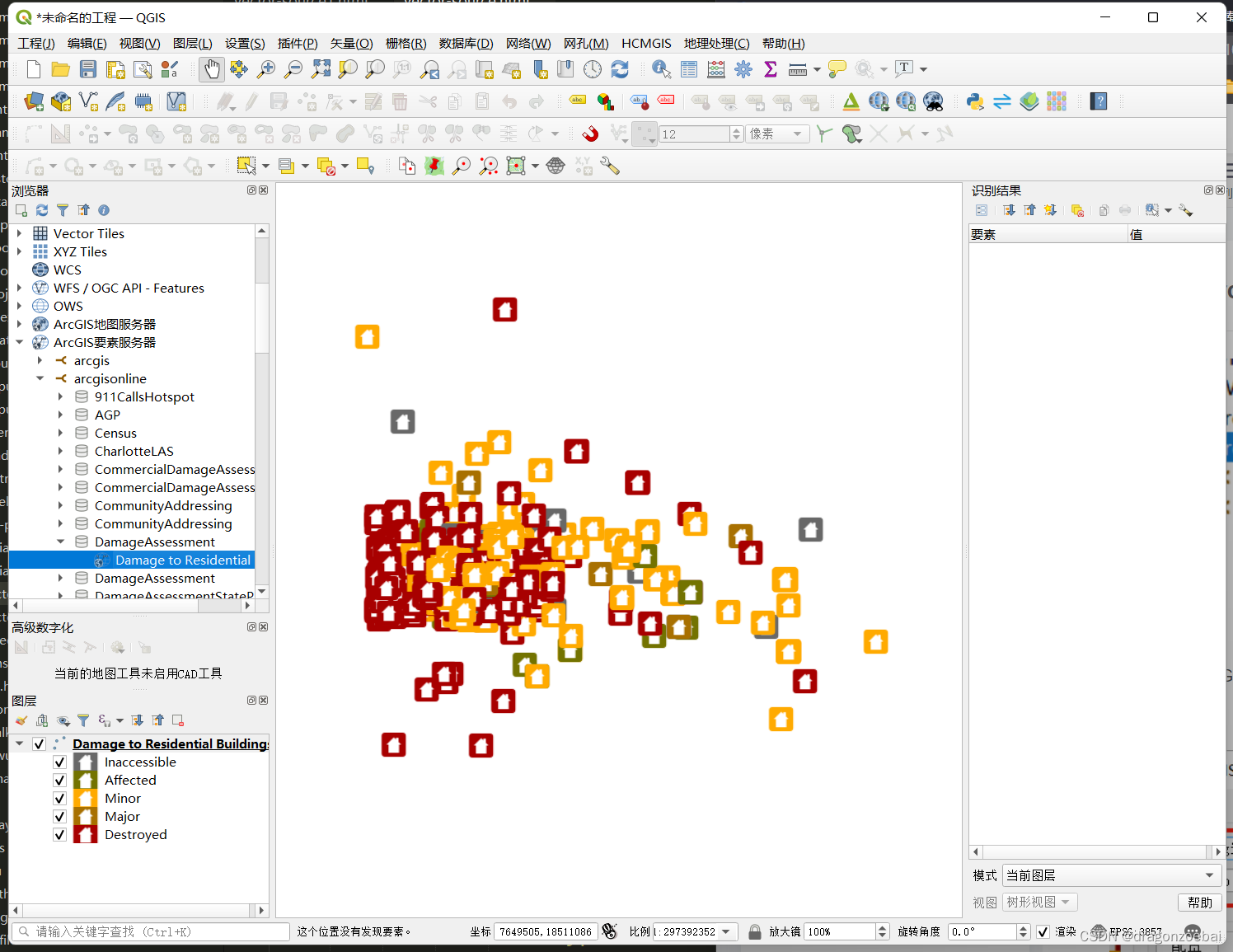
qgis添加arcgis的FeatureServer
左侧浏览器-ArcGIS要素服务器-新建连接 http://sampleserver6.arcgisonline.com/arcgis/rest/services/ 展开-双击即可...

java进阶---多态
多态的概述 什么是多态 同一个对象,在不同时刻表现出来的不同形态 多态的前提 要有继承或实现关系要有方法的重写要有父类引用指向子类对象 多态的具体实现 对象的多态是多态的核心和重点 规则: 一个对象的编译类型与运行类型可以不一致编译类型在定义对象时,就确定了,…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
