【详解二叉树】
🌠作者:@TheMythWS.
🎇座右铭:不走心的努力都是在敷衍自己,让自己所做的选择,熠熠发光。
目录
树形结构
概念
树的示意图
树的基本术语
树的表示
树的应用
二叉树(重点)
二叉树的定义
二叉树的五种不同形态
两种特殊的二叉树
二叉树的性质(重点!!!)
练习题
二叉树的存储
二叉树的基本操作
二叉树的遍历概念理解( (Traversing Binary Tree) )
1.先序遍历(DLR)
2.中序遍历(LDR)
3.后序遍历(LRD)
练习题一
4.层序遍历
练习题二
递归实现-先序中序后序遍历
非递归实现-先序中序后序遍历:
获取树中结点的个数
获取叶子结点(度为0的结点)的个数
获取第K层结点的个数
获取二叉树的高度
检测值为value的元素是否存在
层序遍历
判断一棵树是不是完全二叉树
OJ练习题
树形结构
概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
它具有以下的特点:
- 有一个特殊的结点,称为根(root)结点,根结点没有直接前驱结点, 只有后继结点.
- 除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个直接后继
- 树是递归定义的。
树的示意图
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
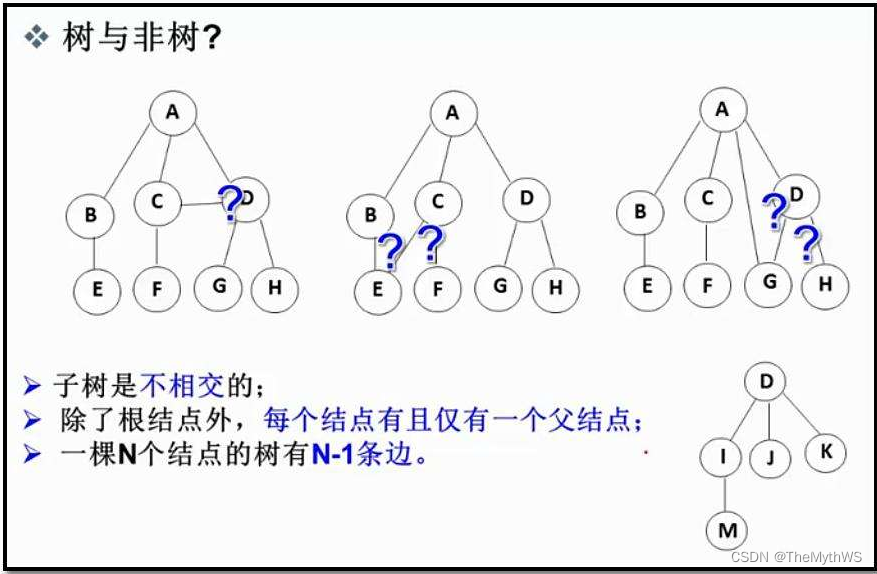
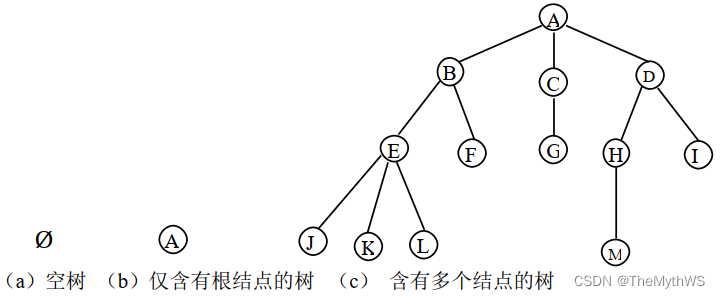
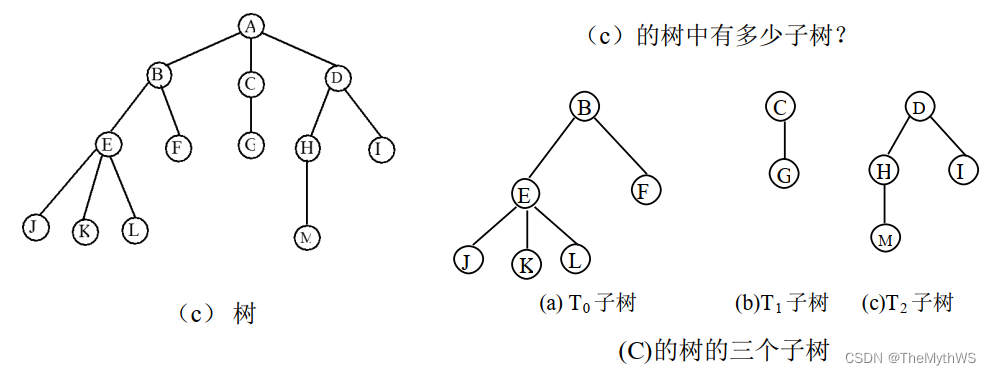
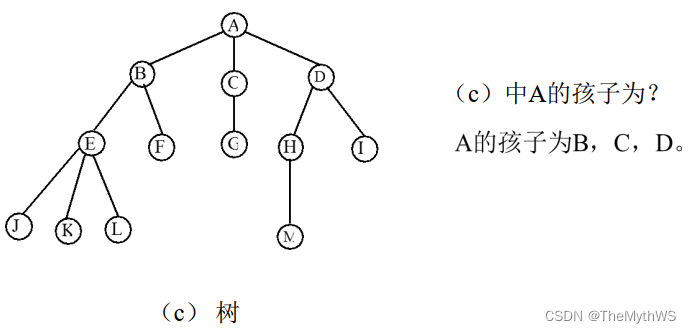
树的基本术语
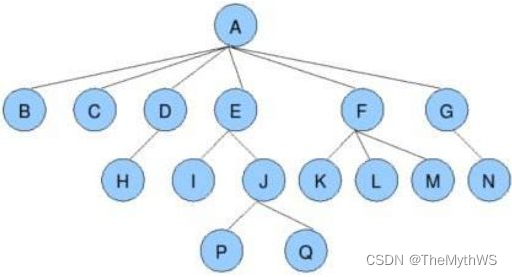
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
树的度:(唯一性)一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
叶子结点或终端结点:度为0的结点称为叶子结点; 如上图:B、C、H、I...等结点点为叶子结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
根结点:一棵树中,没有双亲结点的结点;如上图:A
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4树的以下概念只需了解,只要知道是什么意思即可:
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为堂兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
有序树与无序树:若一棵树中所有子树从左到右的排序是有顺序的,不能颠倒次序,称该树为有序树;反之称为无序树。
森林:由m(m>=0)棵互不相交的树组成的集合称为森林
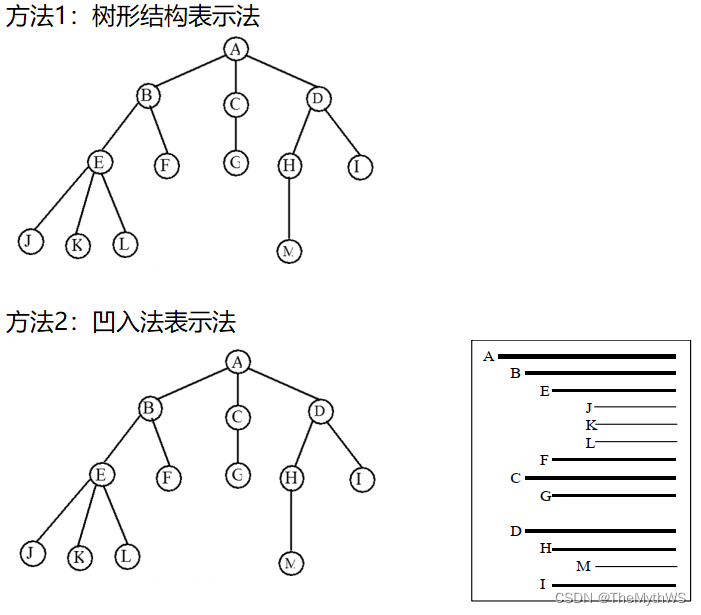
树的表示
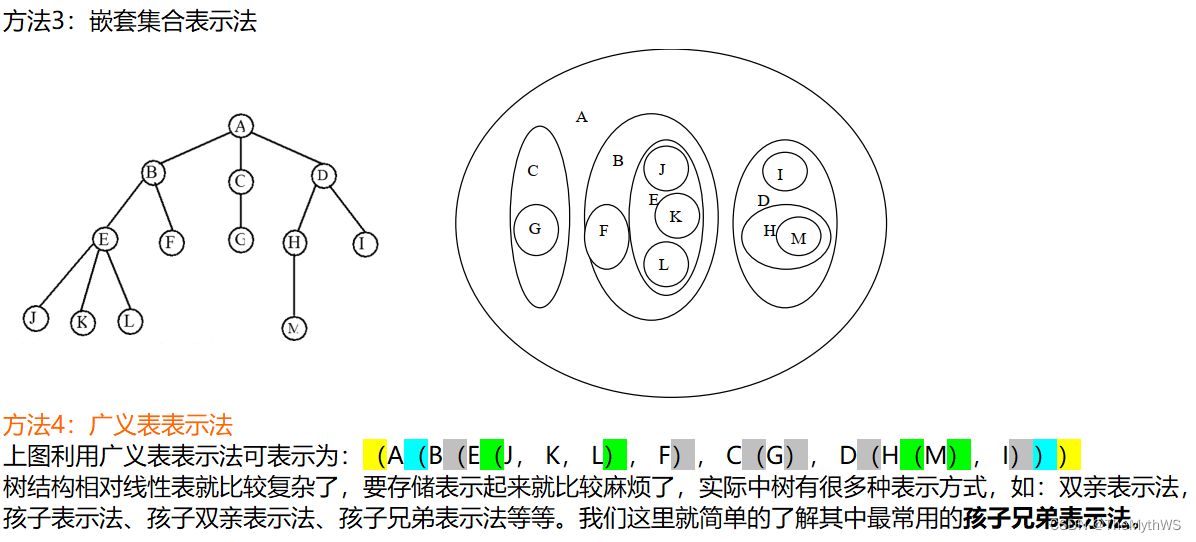
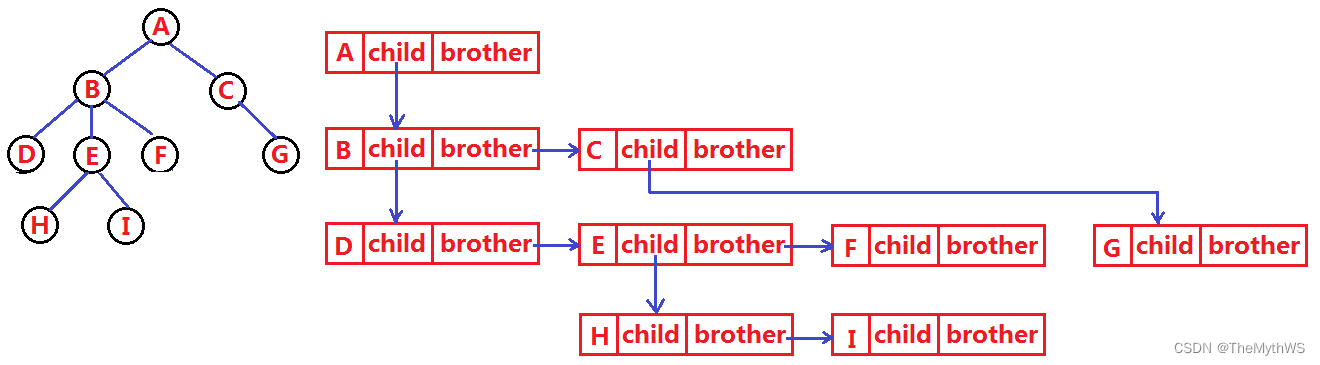
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}
树的应用
文件系统管理(目录和文件)
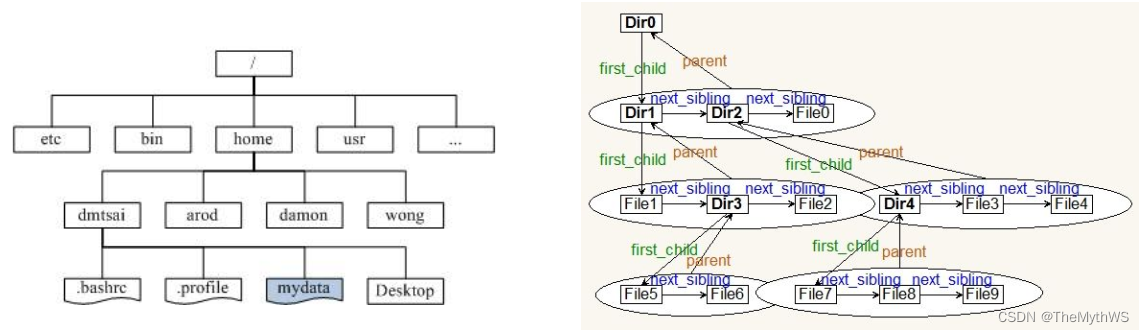
二叉树(重点)
二叉树的定义
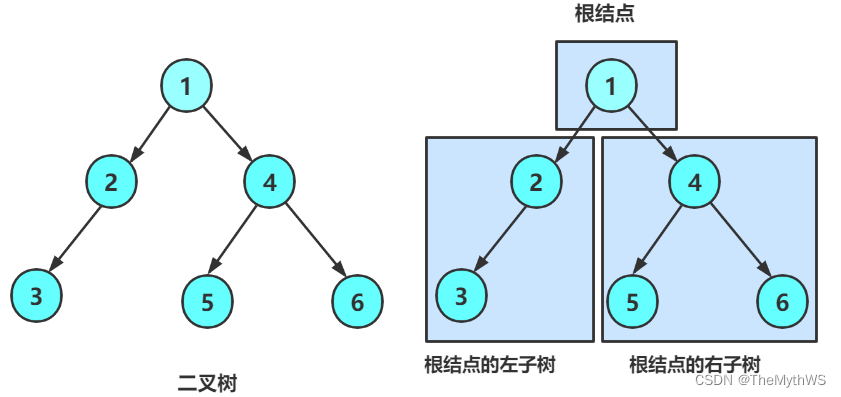
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由一个根结点加上两棵别称为左子树和右子树的互不相交的二叉树组成。
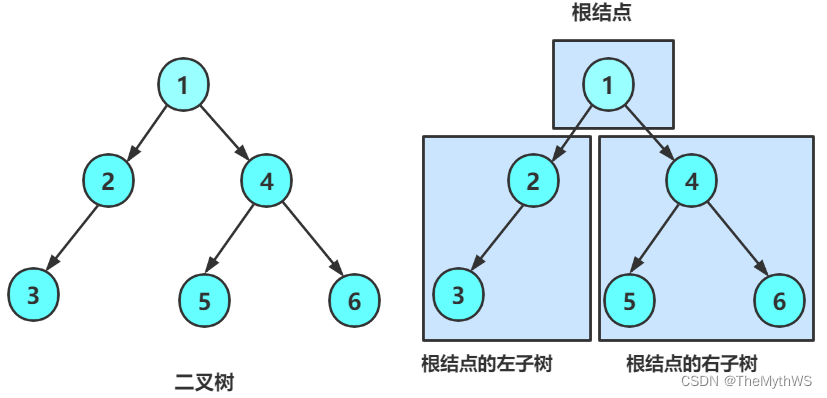
特点:
1) 每个结点的度≤2;
2) 是有序树;
说明: 二叉树的特点是每个结点最多有两个孩子, 或者说, 在二叉树中, 不存在度大于2的结点,
并且二叉树是有序树( 树为无序树), 其子树的顺序不能颠倒。
二叉树的五种不同形态
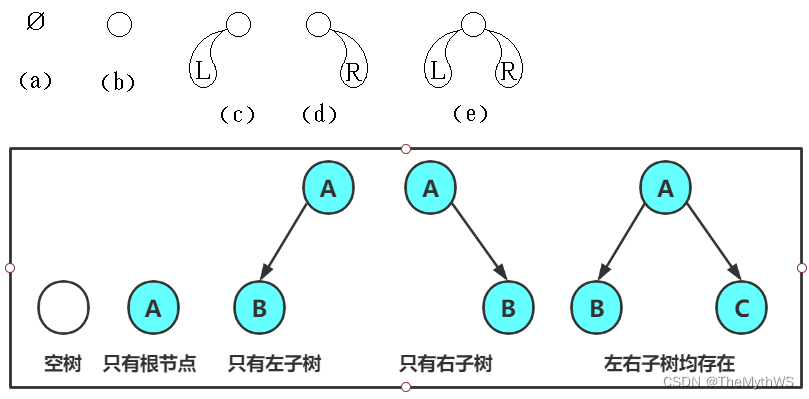
两种特殊的二叉树
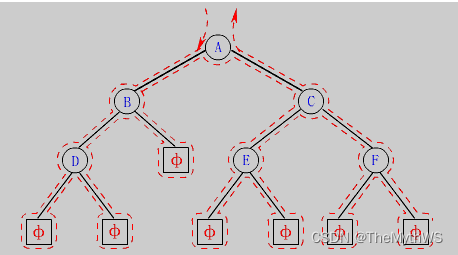
1. 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是2^k - 1,则它就是满二叉树。
2. 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。
要注意的是满二叉树是一种特殊的完全二叉树。
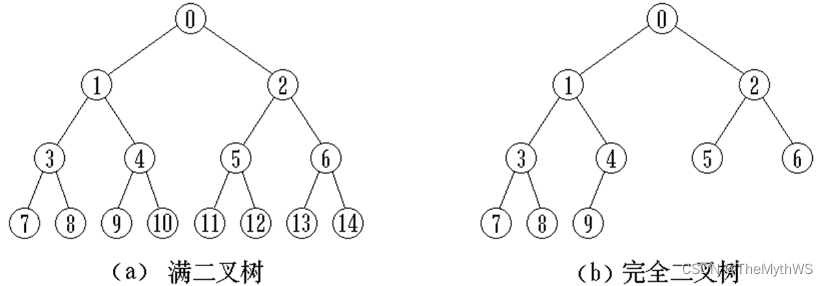
二叉树的性质(重点!!!)
练习题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数n0为( )
A 不存在这样的二叉树
B 200
C 198
D 199
n0 = n2 + 1 = 2002.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一个具有767个结点的完全二叉树,其叶子结点个数为()
A 383
B 384
C 385
D 386
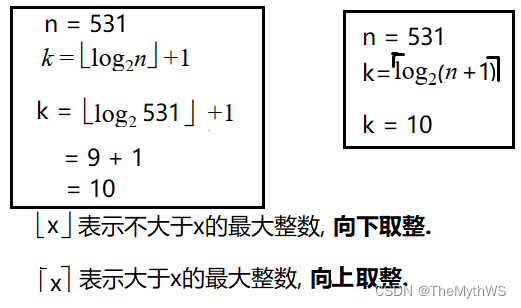
奇数个结点的完全二叉树说明没有度为1的结点, 则767 = n0 + n2, n0 = n2 + 1, n2 = n0 - 1, 767 = 2n0 - 1, n0 = 384.4.一棵完全二叉树的结点数为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
二叉树的存储
顺序存储结构(数组表示)
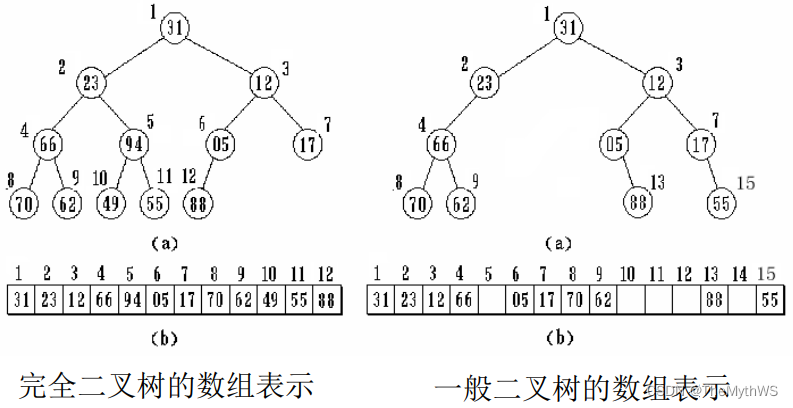
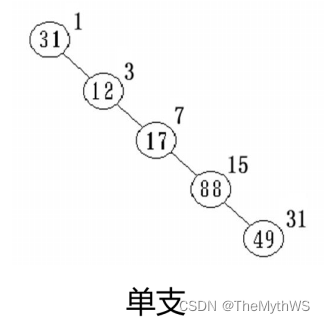
链式存储结构(指针表示)
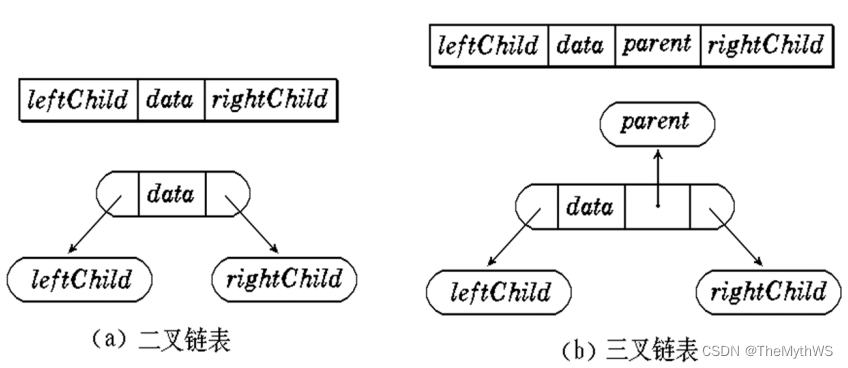
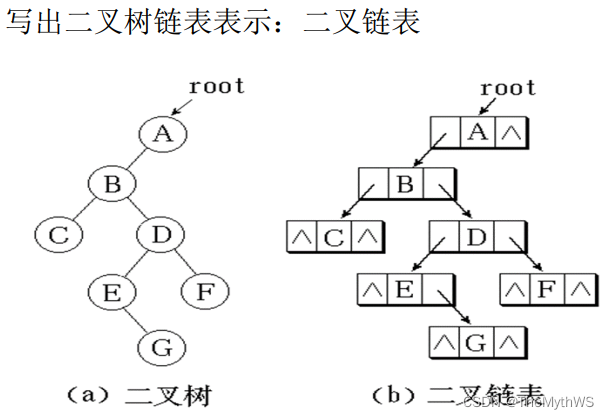
二叉树的链式存储是通过一个一个的结点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前结点的根结点
}二叉树的基本操作
前置说明
此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
public class BinaryTree {public static class BTNode {BTNode left;BTNode right;int value;BTNode(int value) {this.value = value;}}private BTNode root;public void createBinaryTree() {BTNode node1 = new BTNode(1);BTNode node2 = new BTNode(2);BTNode node3 = new BTNode(3);BTNode node4 = new BTNode(4);BTNode node5 = new BTNode(5);BTNode node6 = new BTNode(6);root = node1;node1.left = node2;node2.left = node3;node1.right = node4;node4.left = node5;node4.right = node6;}public static void main(String[] args) {BinaryTree binaryTree = new BinaryTree();binaryTree.createBinaryTree();}
} 
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解.
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
二叉树的遍历概念理解( (Traversing Binary Tree) )
1.先序遍历(DLR)
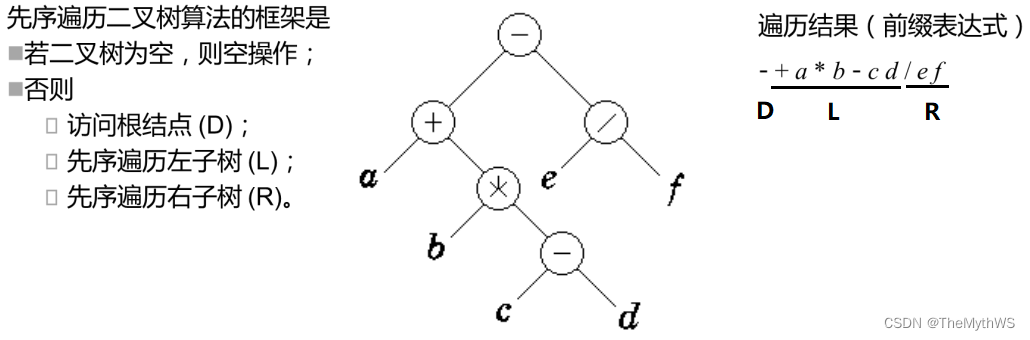
2.中序遍历(LDR)
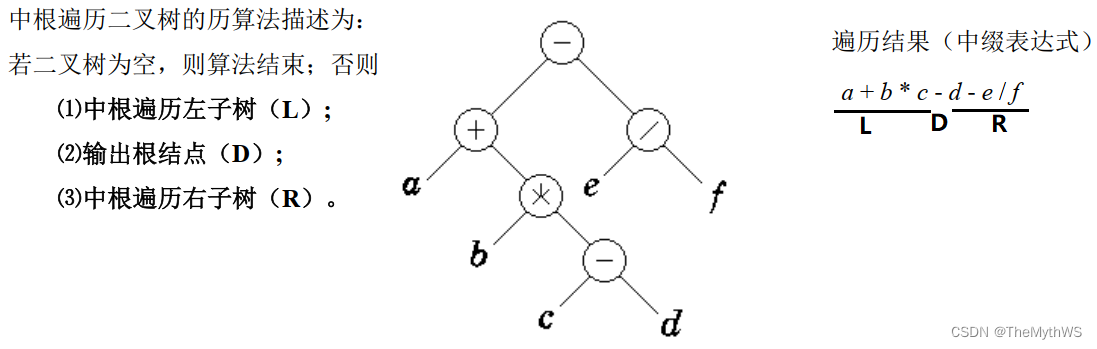
3.后序遍历(LRD)
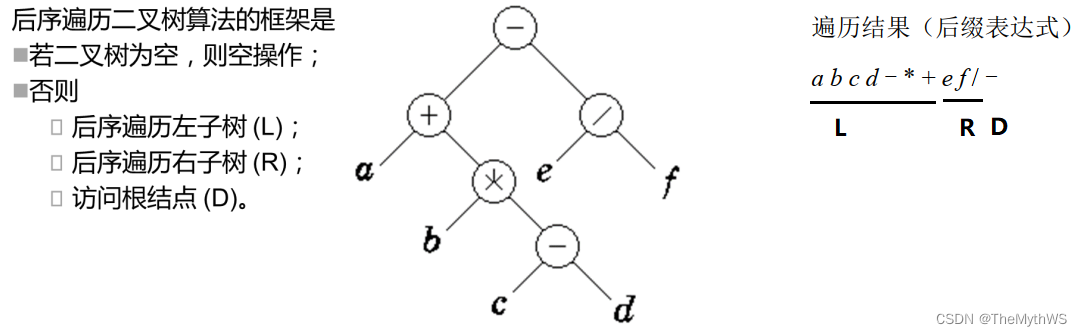
练习题一
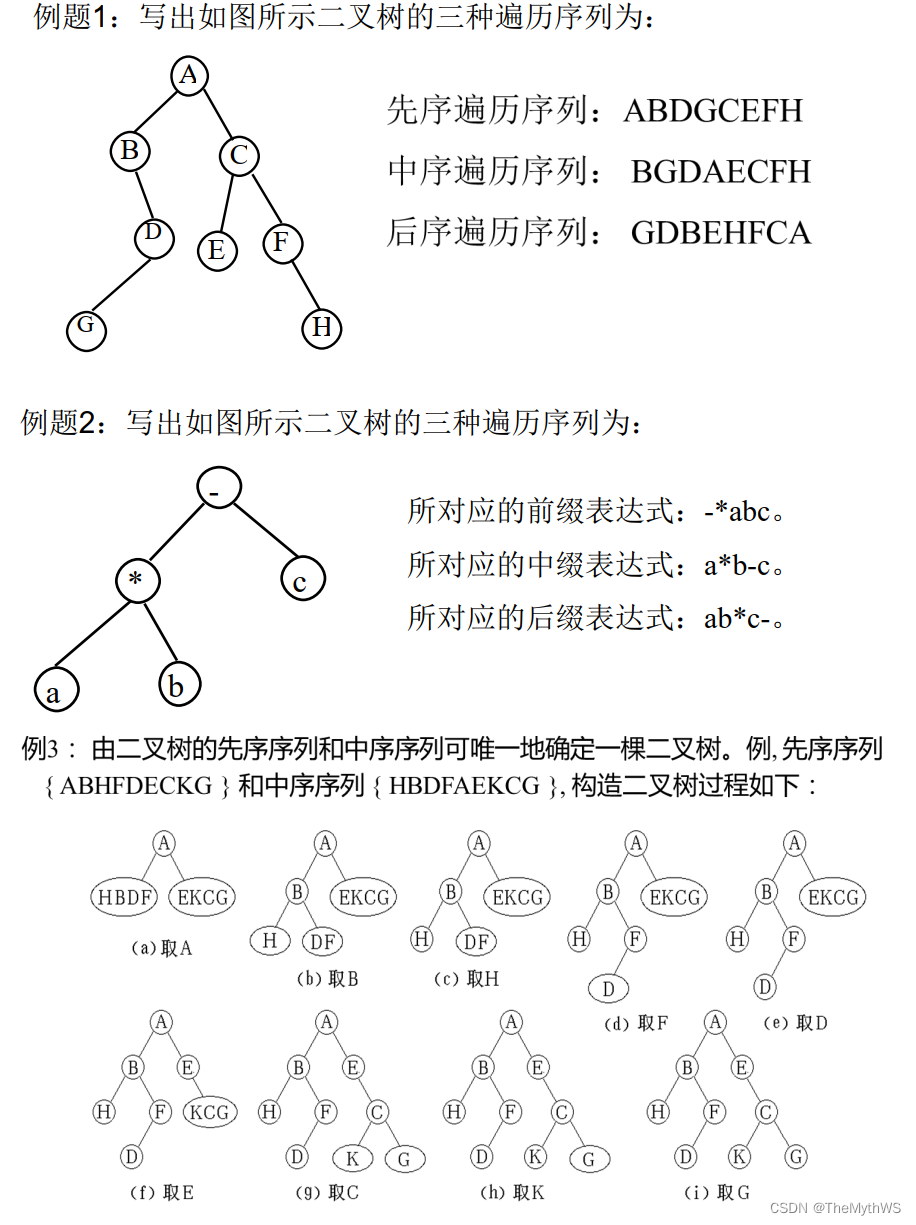
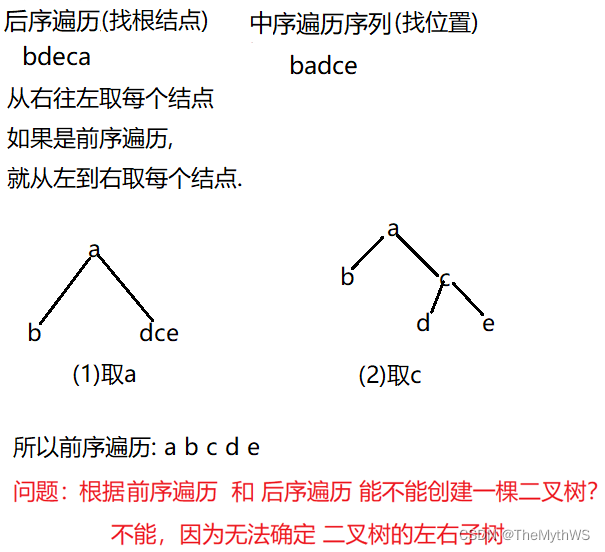
问题1:如何可唯一地确定一棵二叉树?
答:先序(找根)+中序(找位置) 或 后序(找根)+中序(找位置)均可唯一地确定一棵二叉树
先序 + 后序(X)问题2:二叉树的二叉链表存储结构中,有多少个指针域未利用?
答:二叉树的二叉链表存储结构中,假如有n个结点, 则共有2n个指针域(定义的)
已经使用的有n-1个指针域,所以有2n - (n - 1) = n+1个指针域未利用.
为什么是n - 1?(因为减去了一个根结点, 根结点是没有被指向的, 有n个结点除了根结点, 孩子结点就是n-1个)
4.层序遍历
设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
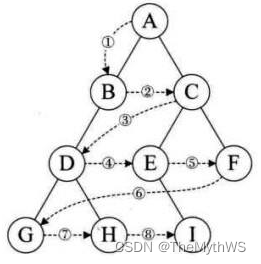
总结:
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。
如果D代表根结点,L代表根结点的左子树,R代表根结点的右子树,则根据遍历根结点的先后次序有以下遍历方式:
- DLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
- LDR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
- LRD:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根结点。
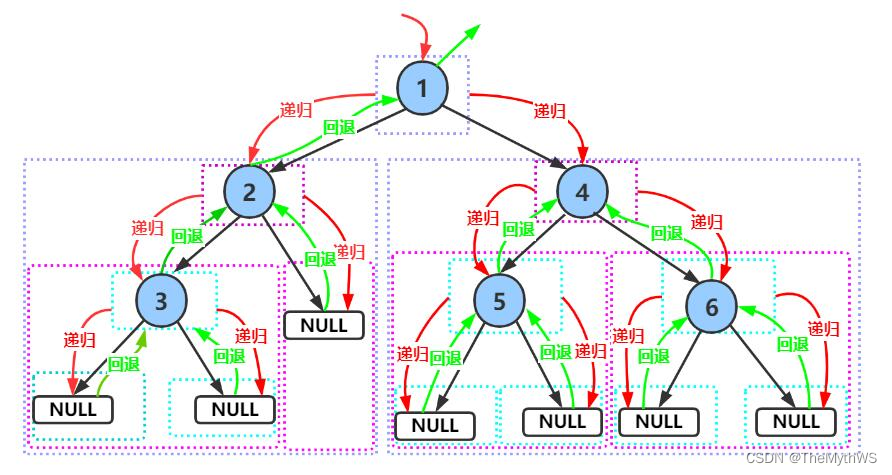
分析前序递归遍历,中序与后序图解类似
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
练习题二
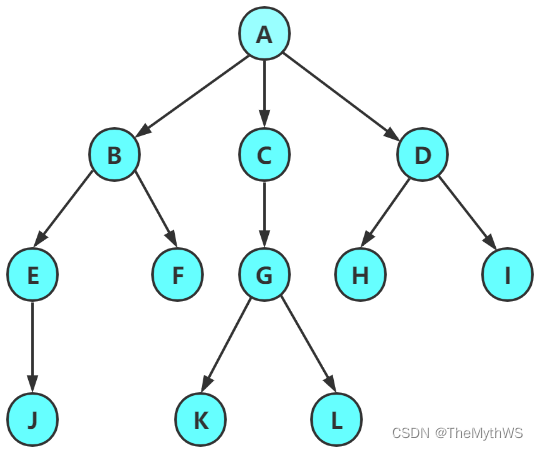
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
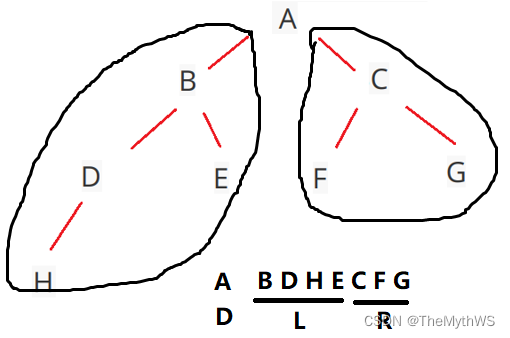
A: E B: F C: G D: H3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde
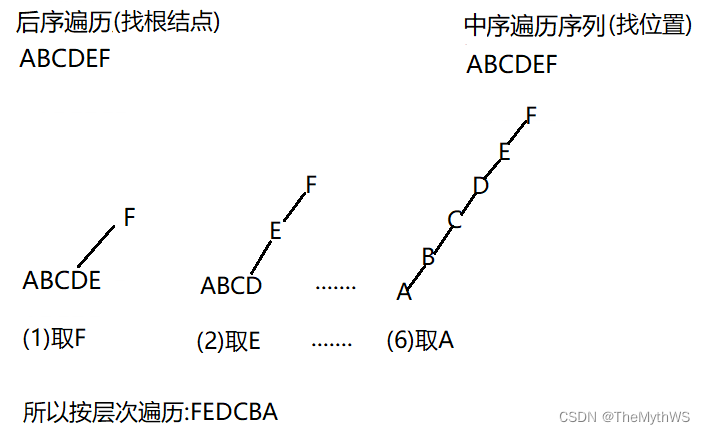
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
递归实现-先序中序后序遍历
我们先基于以下二叉树结构来实现:
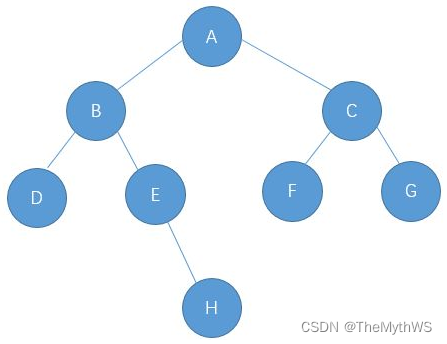
public class TestBinaryTree {static class TreeNode {public char val;//数据域public TreeNode left;//左孩子的引用public TreeNode right;//右孩子的引用public TreeNode(char val) {this.val = val;}}//public TreeNode root;//二叉树的根结点public TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;//this.root = A;return A;}// 前序遍历void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}// 中序遍历void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}// 后序遍历void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}
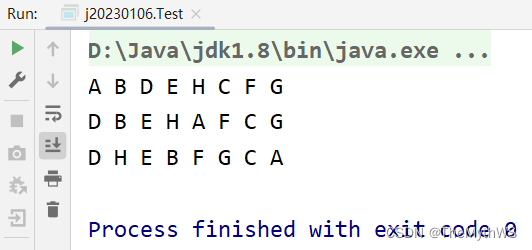
}public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();testBinaryTree.preOrder(root);System.out.println();testBinaryTree.inOrder(root);System.out.println();testBinaryTree.postOrder(root);}
}
非递归实现-先序中序后序遍历:
此次我们对二叉树结构做了微调:
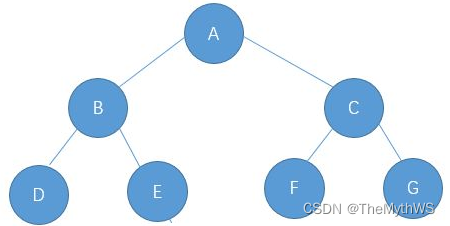
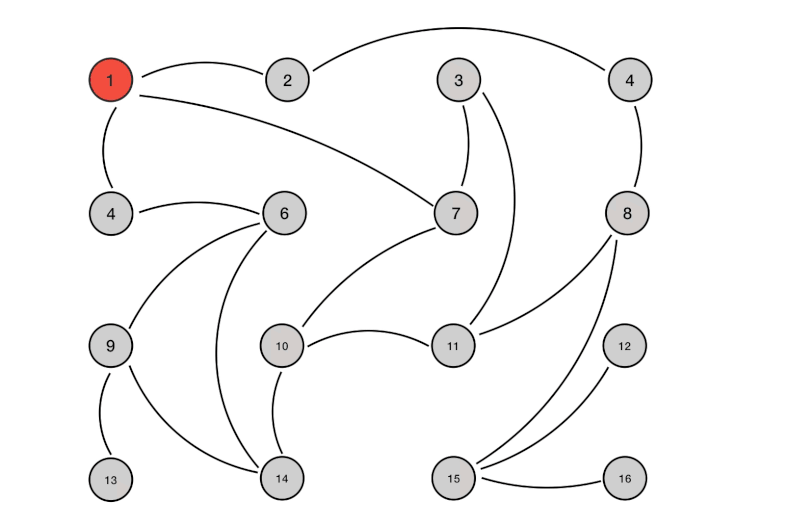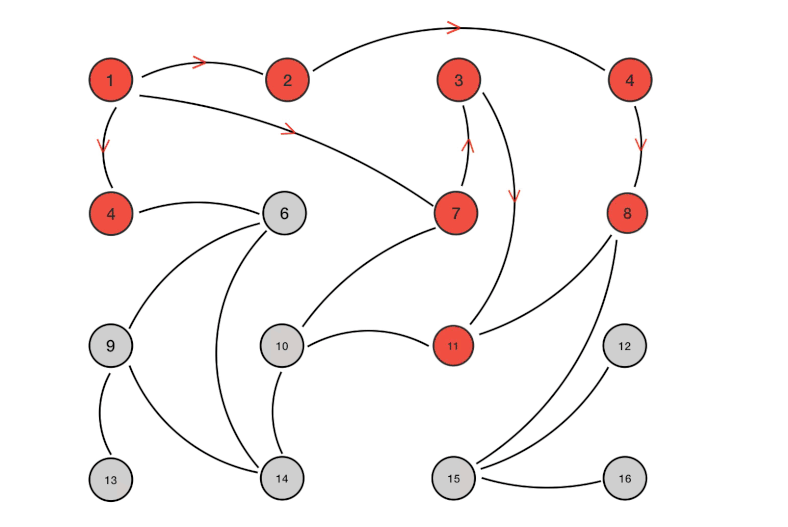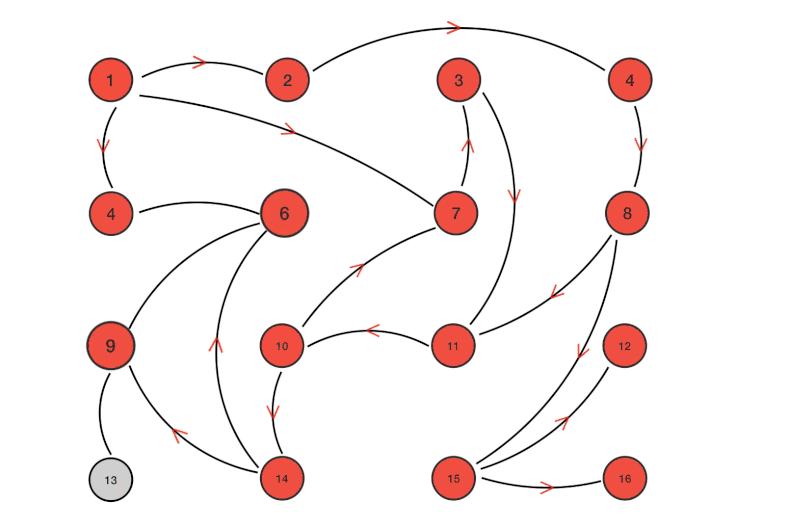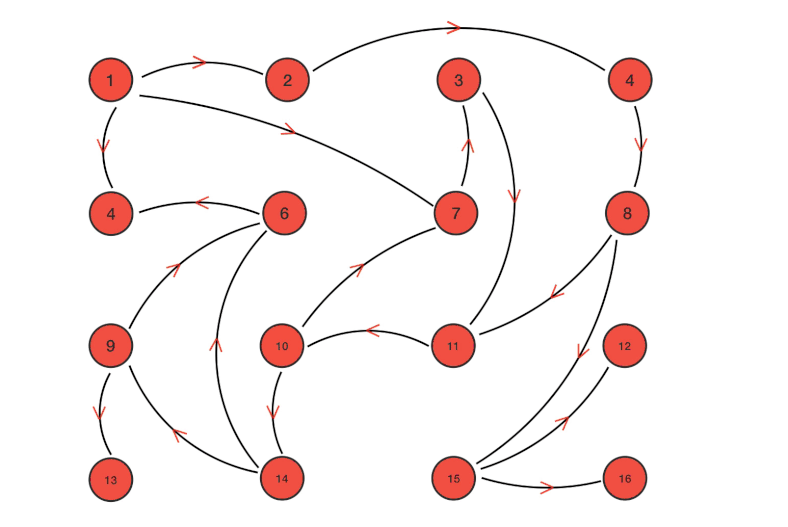
先序图解
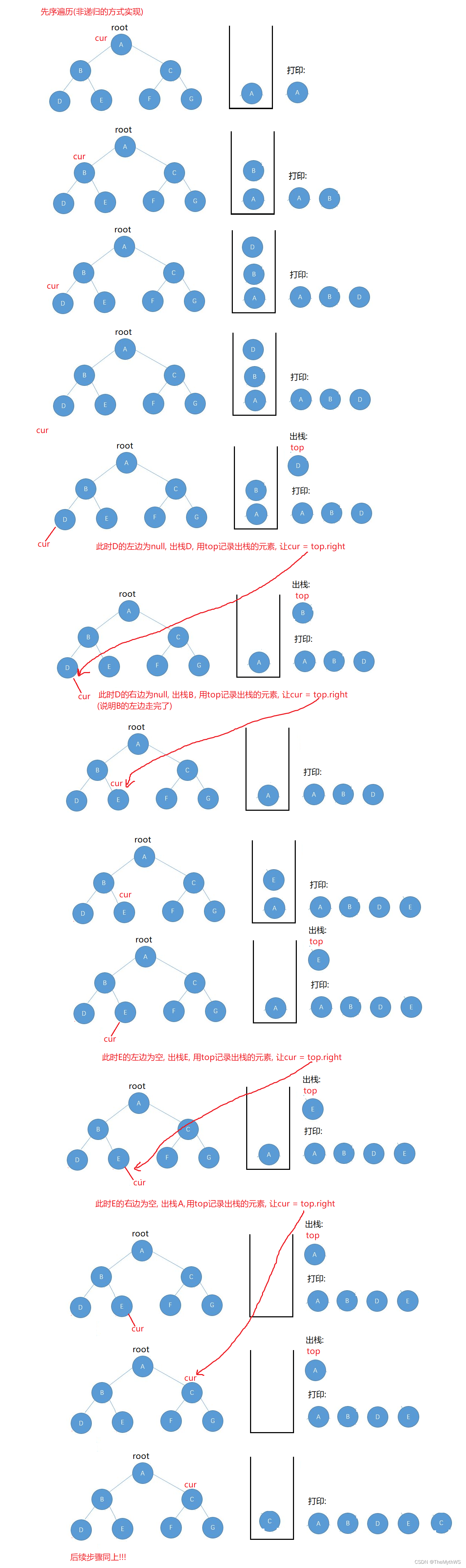
中序图解
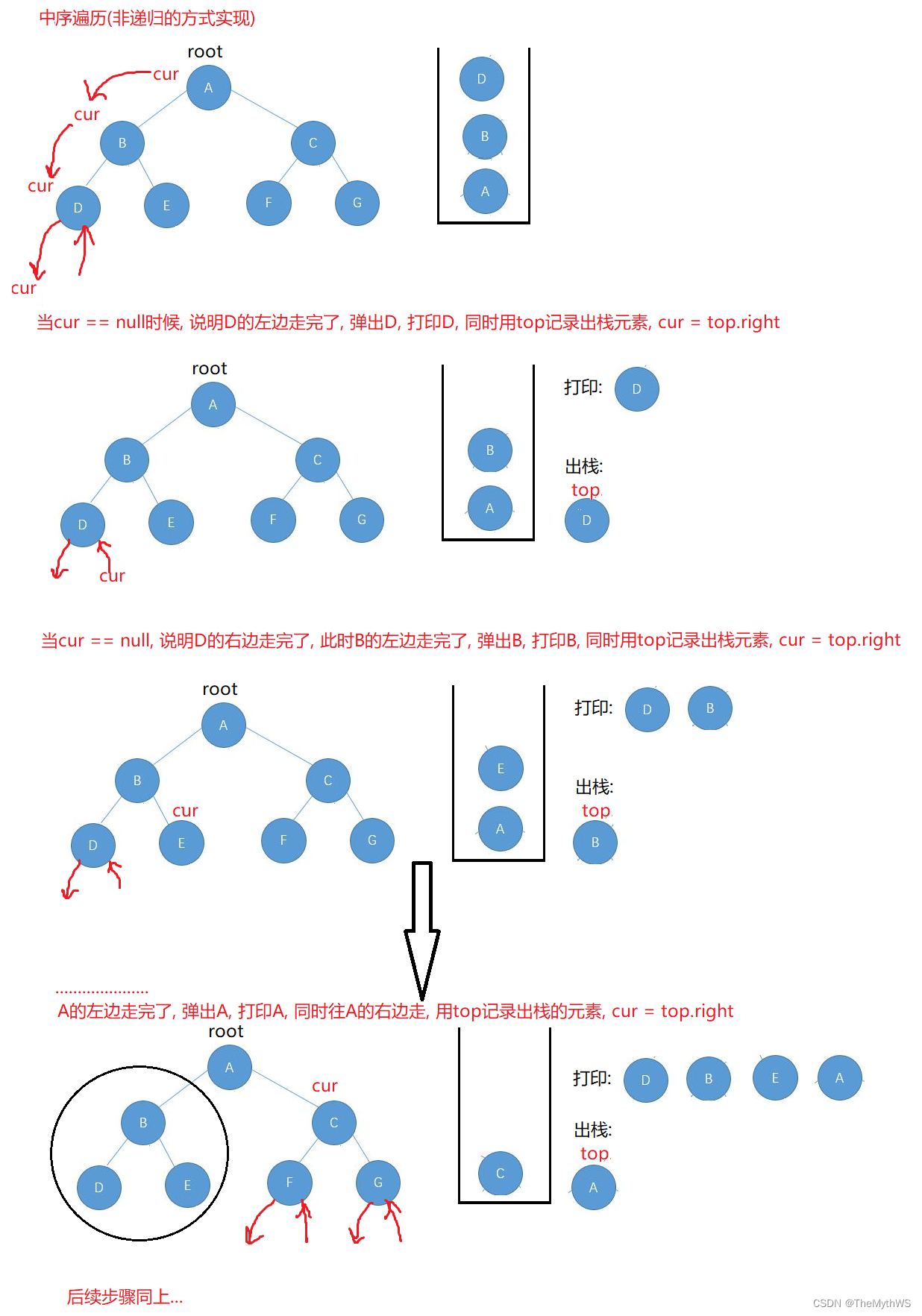
后序图解
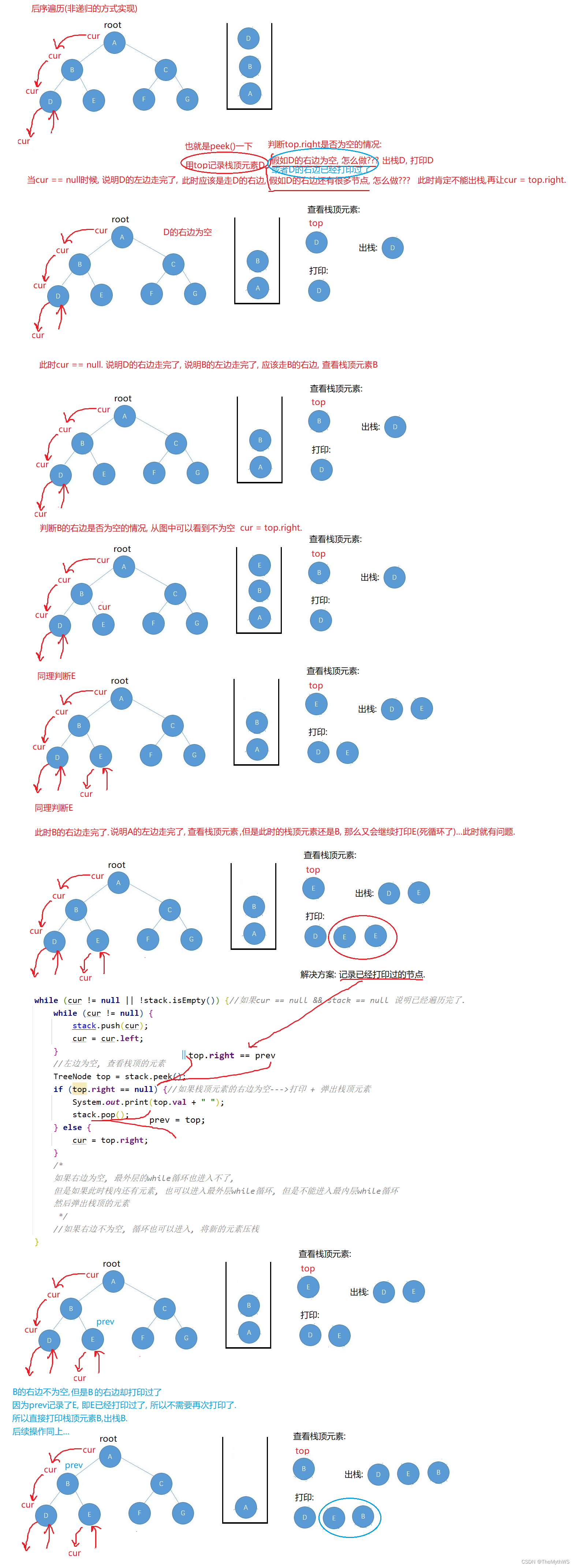
(直接修改创建二叉的代码)
public TreeNode createTree2() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;//E.right = H;//this.root = A;return A;}//非递归实现前序遍历:public void preOrderNor(TreeNode root) {if (root == null) {return;}TreeNode cur = root;Deque<TreeNode> stack = new ArrayDeque<>();while (cur != null || !stack.isEmpty()) {//如果cur == null && stack == null 说明已经遍历完了.while (cur != null) {stack.push(cur);System.out.print(cur.val + " ");cur = cur.left;}//左边为空, 弹出栈顶的元素TreeNode top = stack.pop();cur = top.right;/*如果右边为空, 最外层的while循环也进入不了,但是如果此时栈内还有元素, 也可以进入最外层while循环, 但是不能进入最内层while循环然后弹出栈顶的元素*///如果右边不为空, 循环也可以进入, 将新的元素压栈}}//非递归实现中序遍历:public void inOrderNor(TreeNode root) {if (root == null) {return;}TreeNode cur = root;Deque<TreeNode> stack = new ArrayDeque<>();while (cur != null || !stack.isEmpty()) {//如果cur == null && stack == null 说明已经遍历完了.while (cur != null) {stack.push(cur);cur = cur.left;}//左边为空, 弹出栈顶的元素TreeNode top = stack.pop();System.out.print(top.val + " ");cur = top.right;/*如果右边为空, 最外层的while循环也进入不了,但是如果此时栈内还有元素, 也可以进入最外层while循环, 但是不能进入最内层while循环然后弹出栈顶的元素*///如果右边不为空, 循环也可以进入, 将新的元素压栈}}//非递归实现后序遍历:public void postOrderNor(TreeNode root) {if (root == null) {return;}TreeNode cur = root;TreeNode prev = null;//这个引用用来记录已经打印过的节点Deque<TreeNode> stack = new ArrayDeque<>();while (cur != null || !stack.isEmpty()) {//如果cur == null && stack == null 说明已经遍历完了.while (cur != null) {stack.push(cur);cur = cur.left;}//左边为空, 查看栈顶的元素TreeNode top = stack.peek();if (top.right == null || top.right == prev) {//如果栈顶元素的右边为空或者栈顶元素的右边已经打印过--->直接打印 + 弹出这个栈顶元素,不需要要再往后遍历不然会重复打印,顺便记录刚刚这个栈顶元素也被打印过了,下次也不要打印它了System.out.print(top.val + " ");stack.pop();prev = top;} else {cur = top.right;}/*如果右边为空, 最外层的while循环也进入不了,但是如果此时栈内还有元素, 也可以进入最外层while循环, 但是不能进入最内层while循环然后查看栈顶的元素, 再判断.*///如果右边不为空, 循环也可以进入, 将新的元素压栈}}
public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree2();testBinaryTree.preOrderNor(root);System.out.println();testBinaryTree.inOrderNor(root);System.out.println();testBinaryTree.postOrderNor(root);}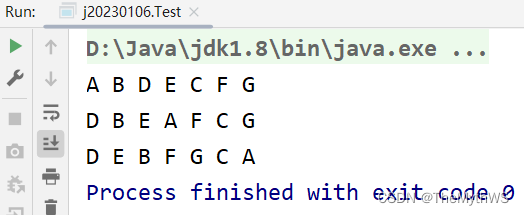
接下来我们用以下二叉树结构进行其它操作

获取树中结点的个数
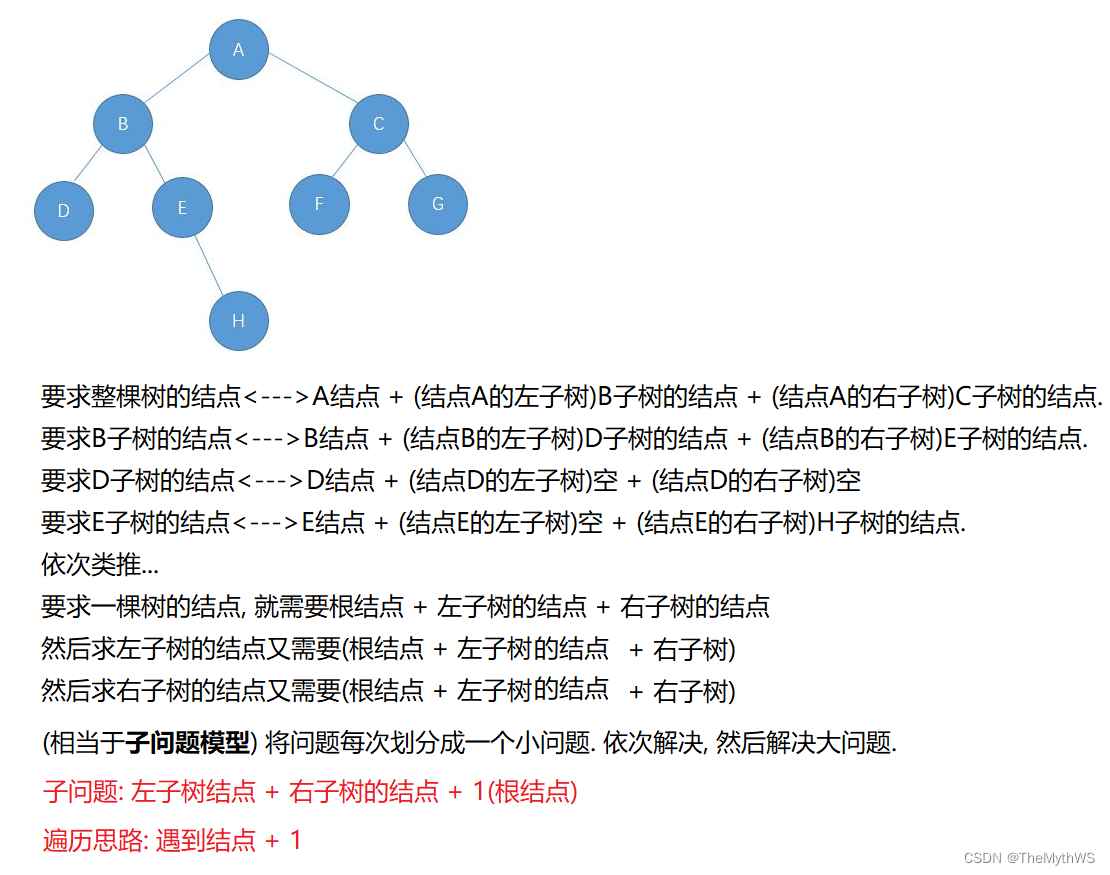
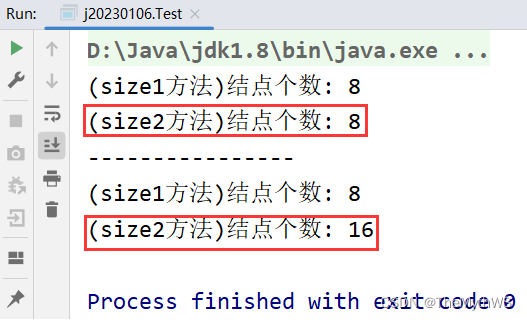
// 获取树中结点的个数// 时间复杂度:O(N)// 空间复杂度:O(logN)满二叉树的情况, 相当于树的高度 ~ O(N)单分支树的情况.int size(TreeNode root) {//子问题思路(左子树结点 + 右子树结点 + 1) 建议写法!if (root == null) {return 0;}int leftSize = size(root.left);int rightSize = size(root.right);return leftSize + rightSize + 1;}public static int nodeSize;//注意这儿有问题, 在OJ上如果有两个树对象测试结点个数, 那么会测试出来的结点个数相同, 因为它们共用nodeSize了.public void size2(TreeNode root) {//遍历思路(遇到结点就 + 1)if (root == null) {return;}nodeSize++;size2(root.left);size2(root.right);}public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();System.out.println("(size1方法)结点个数: " + testBinaryTree.size(root));//8testBinaryTree.size2(root);int nodeSize = TestBinaryTree.nodeSize;System.out.println("(size2方法)结点个数: " + nodeSize);//8System.out.println("----------------");TestBinaryTree testBinaryTree2 = new TestBinaryTree();TestBinaryTree.TreeNode root2 = testBinaryTree2.createTree();System.out.println("(size1方法)结点个数: " + testBinaryTree.size(root));//8testBinaryTree.size2(root);int nodeSize2 = TestBinaryTree.nodeSize;System.out.println("(size2方法)结点个数: " + nodeSize2);//16, 结果有问题, 是因为nodeSize是静态变量, 新建一棵树对象会共用nodeSize, 所以遍历出来的结点个数有问题.}
}
获取叶子结点(度为0的结点)的个数
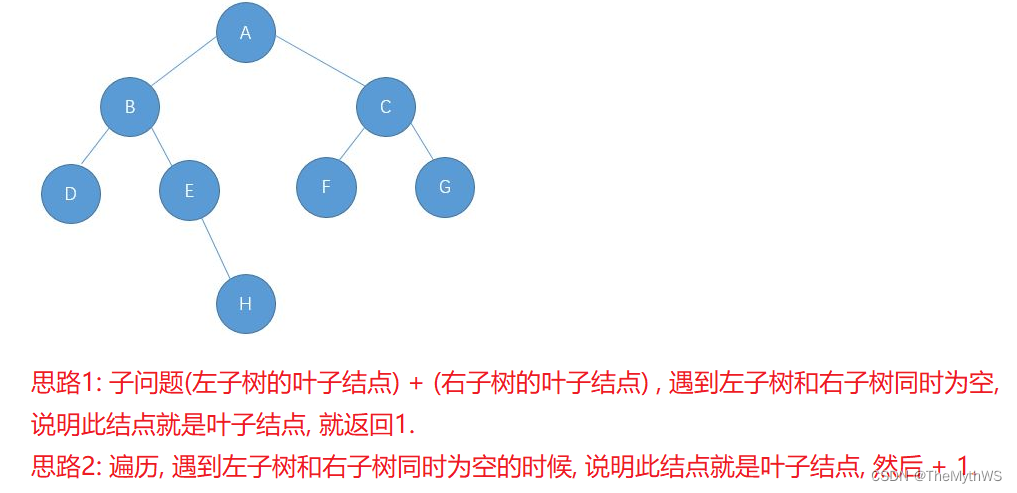
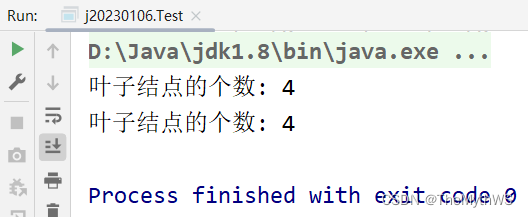
// 获取叶子结点的个数// 子问题:左子树的叶子结点 + 右子树的叶子结点int getLeafNodeCount(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {//遇到叶子结点了.return 1;}int leftSize = getLeafNodeCount(root.left);int rightSize = getLeafNodeCount(root.right);return leftSize + rightSize;}public int leafSize;// 遍历思路:遇到叶子结点就 + 1public void getLeafNodeCount2(TreeNode root) {if (root == null) {return;}if (root.left == null && root.right == null) {//遇到叶子结点了.leafSize++;}getLeafNodeCount2(root.left);getLeafNodeCount2(root.right);}public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();System.out.println("叶子结点的个数: " + testBinaryTree.getLeafNodeCount(root));testBinaryTree.getLeafNodeCount2(root);System.out.println("叶子结点的个数: " + testBinaryTree.leafSize);}
}
获取第K层结点的个数
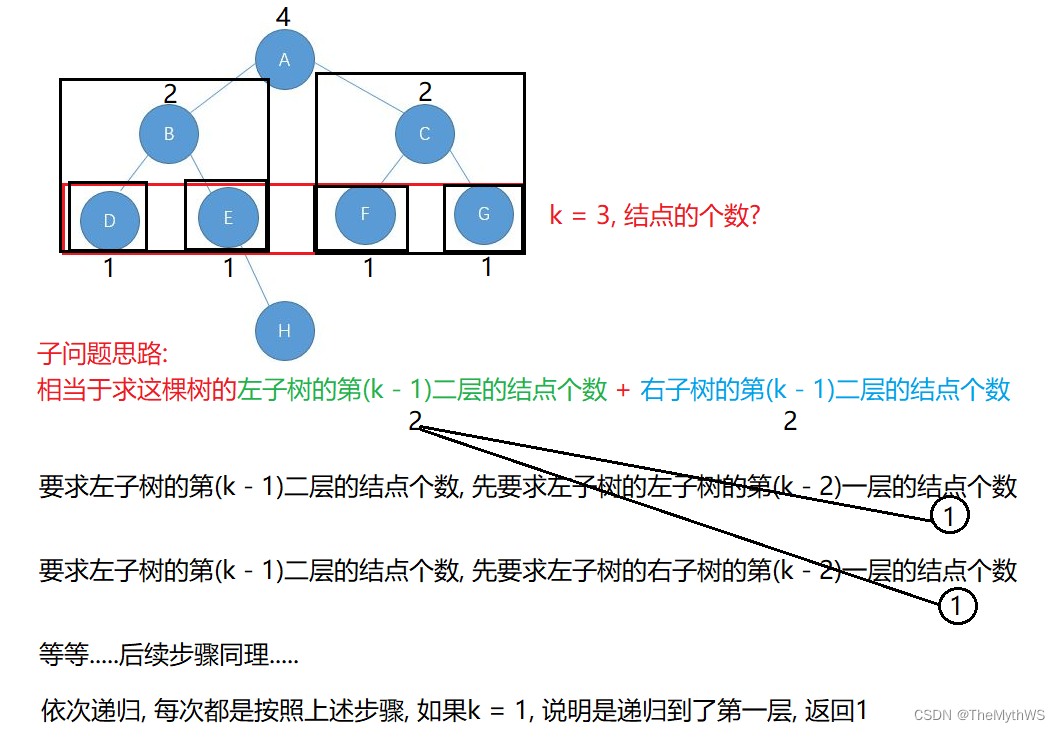
// 获取第K层结点的个数int getKLevelNodeCount(TreeNode root, int k) {if (root == null) {return 0;}if (k == 1) {return 1;}int leftSize = getKLevelNodeCount(root.left, k - 1);int rightSize = getKLevelNodeCount(root.right, k - 1);return leftSize + rightSize;}public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();System.out.println("第k层的结点个数: " + testBinaryTree.getKLevelNodeCount(root, 3));}
}
获取二叉树的高度
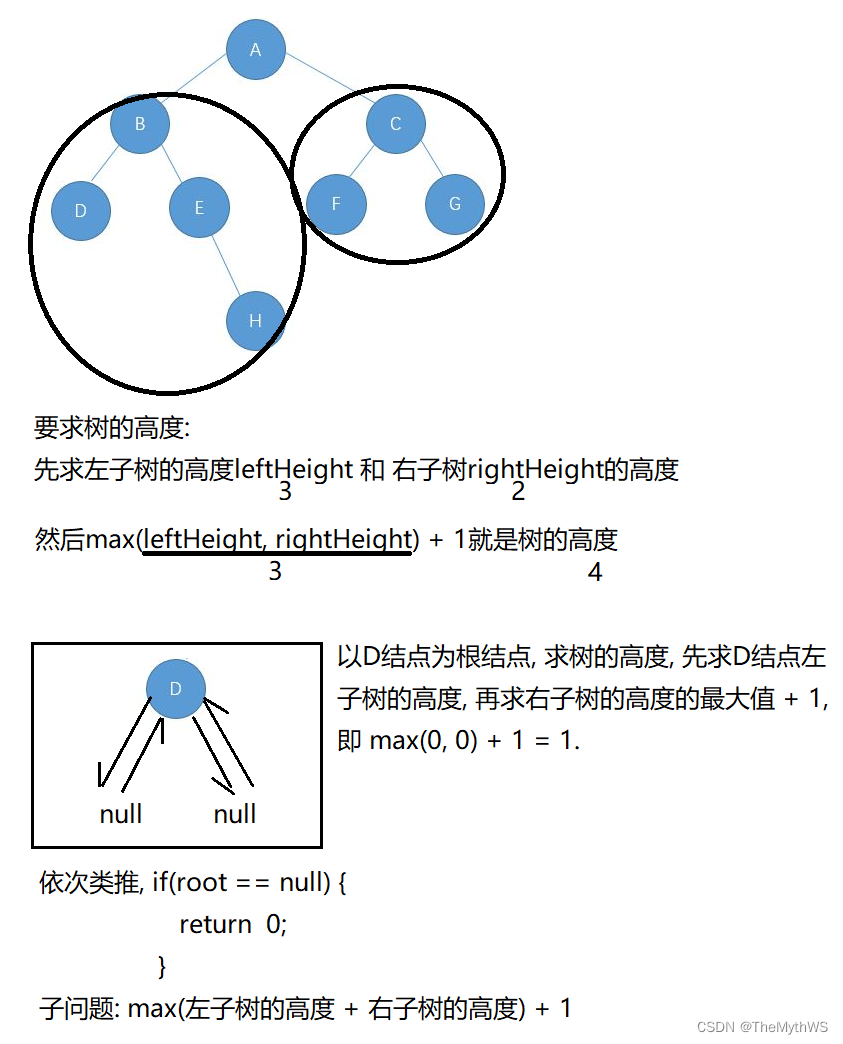
// 获取二叉树的高度// 时间复杂度O(N), 因为每一个结点都会被访问// 空间复杂度O(树的高度)public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;}public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();System.out.println("树的高度: " + testBinaryTree.getHeight(root));}
}
检测值为value的元素是否存在
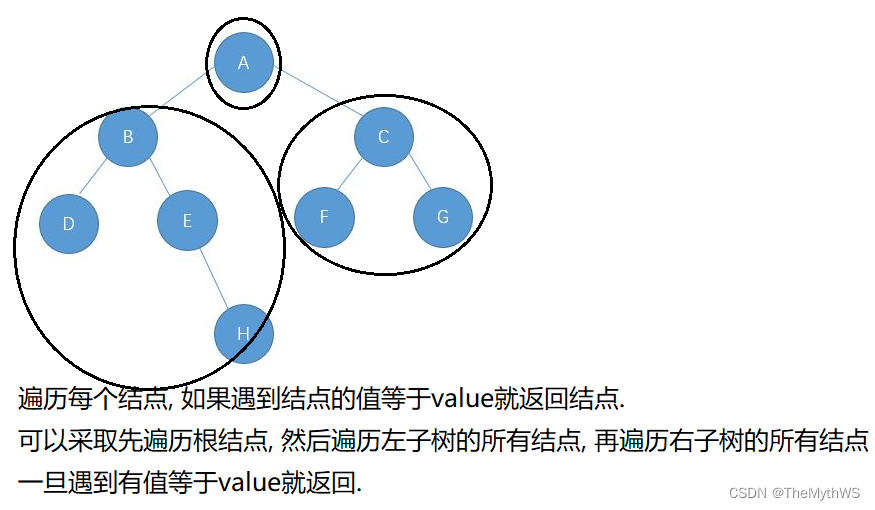
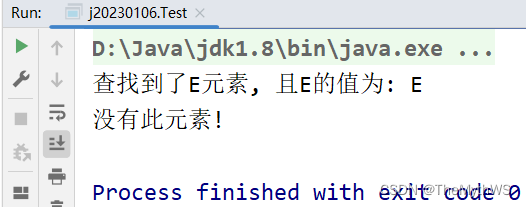
// 检测值为value的元素是否存在public TreeNode find(TreeNode root, int val) {if (root == null) {return null;}if (root.val == val) {return root;}TreeNode leftTree = find(root.left, val);if (leftTree != null) {//左子树找return leftTree;}TreeNode rightTree = find(root.right, val);if (rightTree != null) {//右子树找return rightTree;}return null;//都没找到}public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();TestBinaryTree.TreeNode E = testBinaryTree.find(root, 'E');if (E != null){System.out.println("查找到了E元素, 且E的值为: " + E.val);} else {System.out.println("没有此元素!");}TestBinaryTree.TreeNode J = testBinaryTree.find(root, 'J');if (J != null){System.out.println("查找到了J元素, 且J的值为: " + J.val);} else {System.out.println("没有此元素!");}}
}
层序遍历
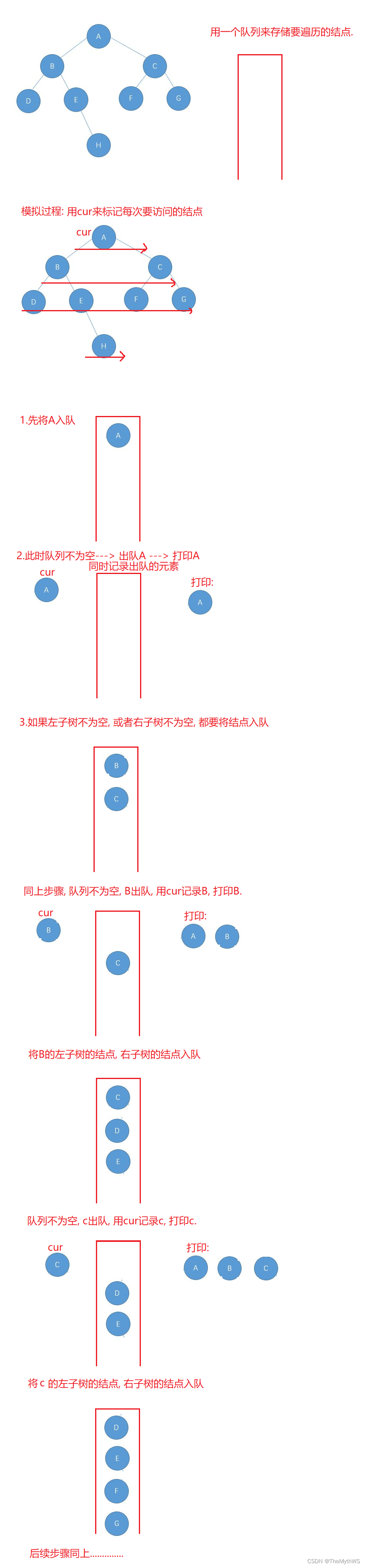
//层序遍历(不带返回值)public void levelOrder(TreeNode root) {if (root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();//先将头结点入队queue.offer(root);while (!queue.isEmpty()) {//队列不为空//出队的同时用cur记录出队的结点, 同时打印出队结点的valueTreeNode cur = queue.poll();System.out.print(cur.val + " ");//如果cur的左子树和右子树有结点就入队if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}}
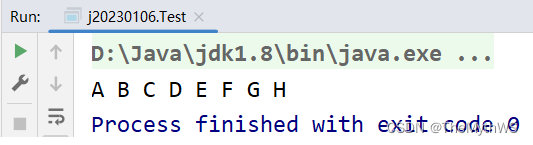
public class Test {public static void main(String[] args) {TestBinaryTree testBinaryTree = new TestBinaryTree();TestBinaryTree.TreeNode root = testBinaryTree.createTree();testBinaryTree.levelOrder(root);}
} 
判断一棵树是不是完全二叉树

boolean isCompleteTree(TreeNode root){if (root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();if (cur != null) {queue.offer(cur.left);queue.offer(cur.right);} else {break;}}//走到这儿说明cur == nullwhile (!queue.isEmpty()) {TreeNode tmp = queue.poll();if (tmp != null) {//队列里剩余的元素不全是null, 说明不是完全二叉树return false;}}return true;}OJ练习题
1. 检查两颗树是否相同。
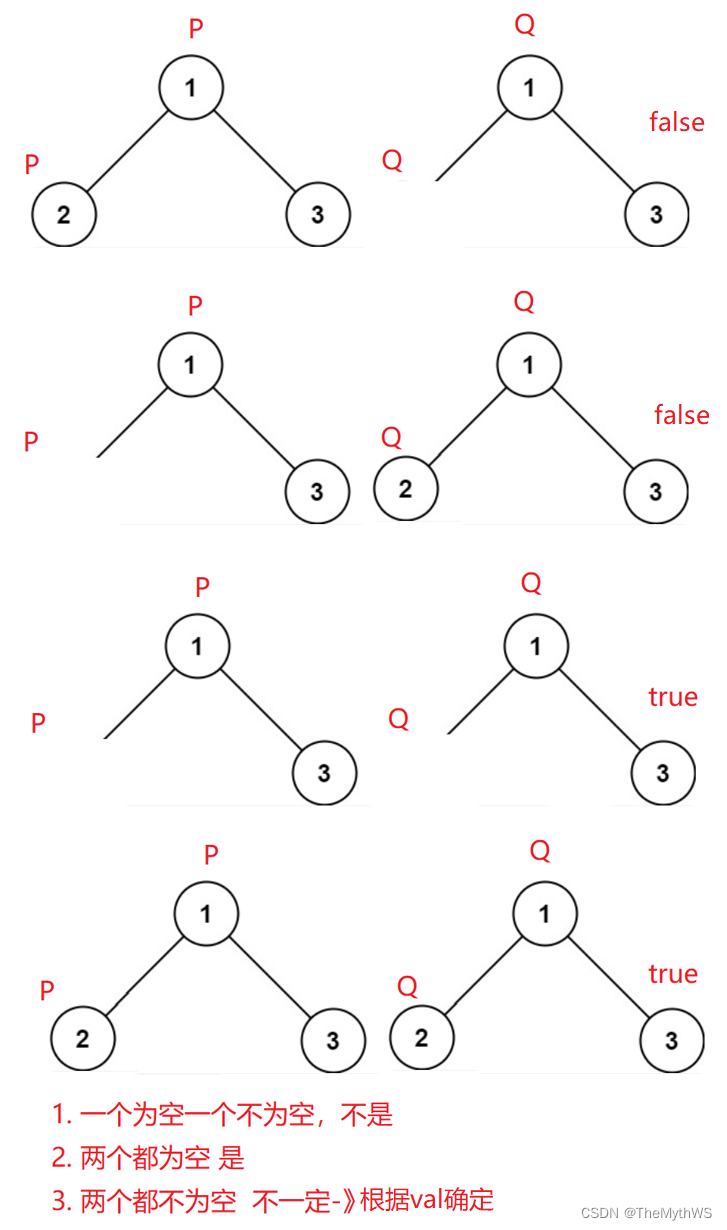
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//检查两棵树是否相同//时间复杂度和空间复杂度: O(min(m, n)) m 和 n是结点的个数//如果一颗树的结点多 一颗树的结点少 必然是不相等的, 所以只需要遍历完结点少的树就行了, 不需要去遍历剩下的结点.//如果两个树的结点一样, min(m, n) 结果都一样, 大不了最坏情况就O(n)public boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q != null || p != null && q == null) {return false;}//走到这里 要么都是空 要么都不是空if (p == null && q == null) {//都是空return true;}if (p.val != q.val) {//都不是空, 在判断值是否相等return false;}//p q都不是空, 且值一样, 当前只是判断了根结点是否相同, 所以下面还要进行递归判断左子树和右子树是否一样.return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}
}2.另一颗树的子树。
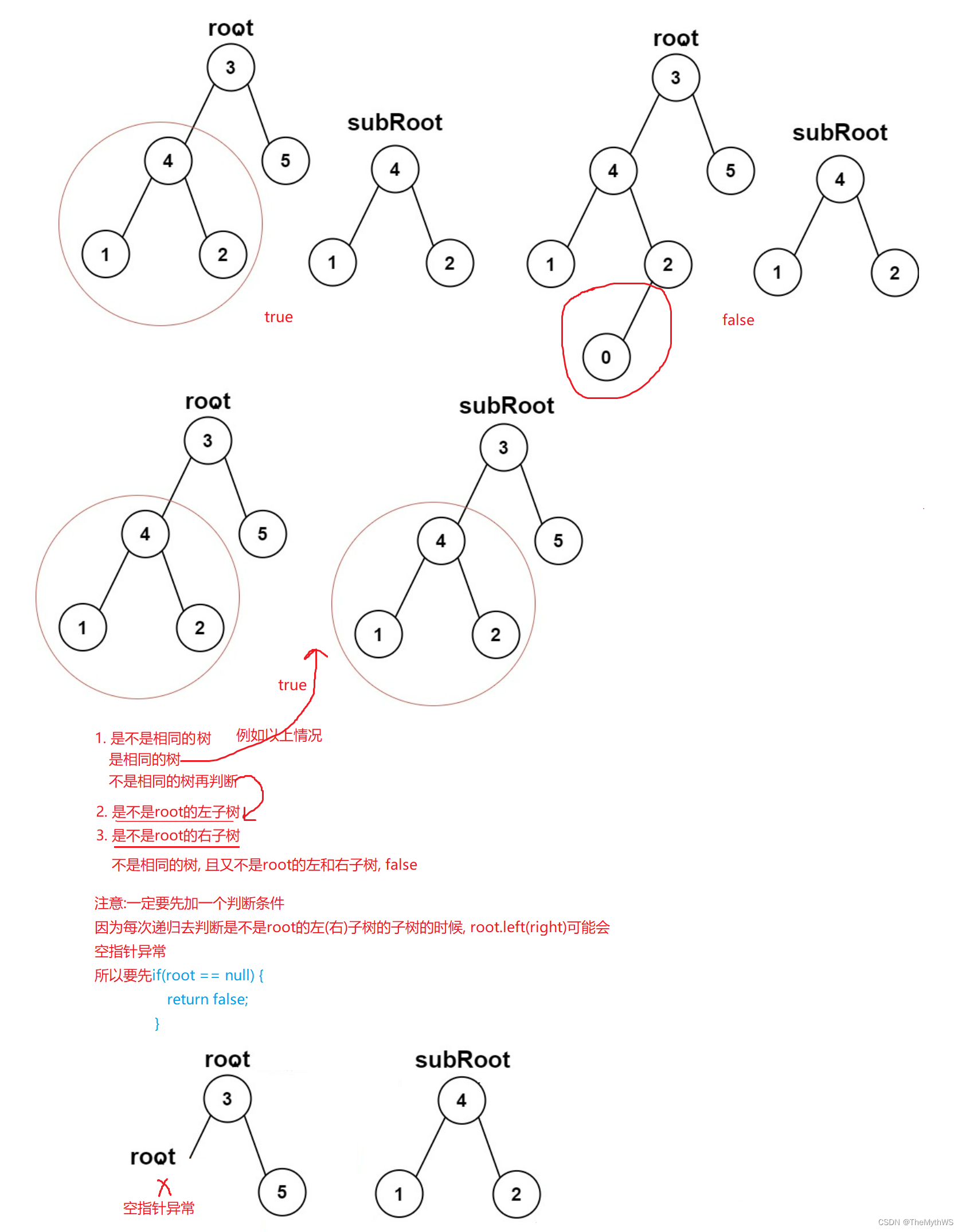
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//时间复杂度:O(S * T) 对于S上的每一个点都需要做一次深度优先搜索来和T匹配, 匹配一次的时间复杂度是O(T)//空间复杂度:O(max(ds, dt)), ds 和 dt分别代表两棵树的深度public boolean isSubtree(TreeNode root, TreeNode subRoot) {if (root == null) {return false;}if (isSameTree(root, subRoot)) {return true;}if (isSubtree(root.left, subRoot)) {return true;}if (isSubtree(root.right, subRoot)) {return true;}return false;}//检查两棵树是否相同//时间复杂度和空间复杂度: O(min(m, n)) m 和 n是结点的个数//如果一颗树的结点多 一颗树的结点少 必然是不相等的, 所以只需要遍历完结点少的树就行了, 不需要去遍历剩下的结点.//如果两个树的结点一样, min(m, n) 结果都一样, 大不了最坏情况就O(n)public boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q != null || p != null && q == null) {return false;}//走到这里 要么都是空 要么都不是空if (p == null && q == null) {//都是空return true;}if (p.val != q.val) {//都不是空, 在判断值是否相等return false;}//p q都不是空, 且值一样, 当前只是判断了根结点是否相同, 所以下面还要进行递归判断左子树和右子树是否一样.return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}
}3. 翻转二叉树。
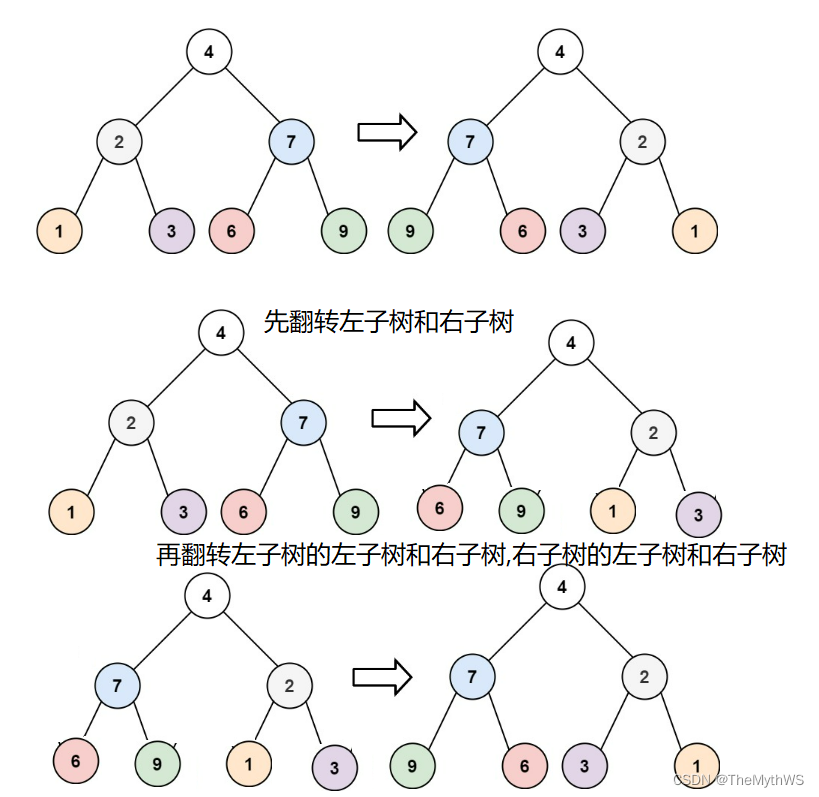
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}//方法1:利用临时结点来存储要交换的结点值
// TreeNode tmpNode = root.left;
// root.left = root.right;
// root.right = tmpNode;
// //递归进行翻转
// invertTree(root.left);
// invertTree(root.right);//方法2:利用返回值TreeNode left = invertTree(root.left);TreeNode right = invertTree(root.right);//翻转root.left = right;root.right = left;return root;}
}4. 判断一颗二叉树是否是平衡二叉树。
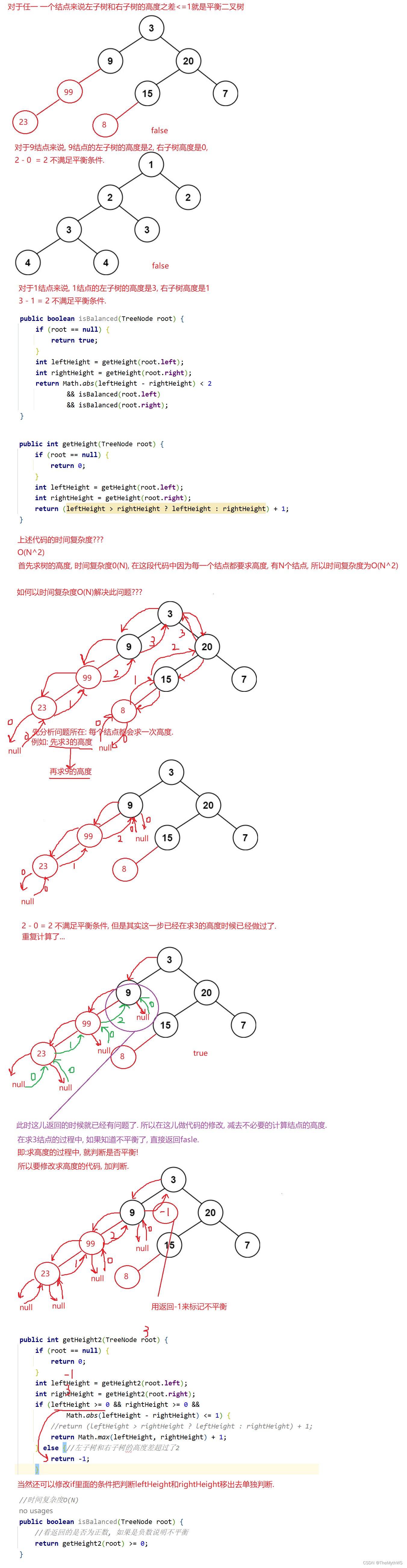
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isBalanced1(TreeNode root) {if (root == null) {return true;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return Math.abs(leftHeight - rightHeight) < 2&& isBalanced1(root.left)&& isBalanced1(root.right);}// 获取二叉树的高度// 时间复杂度O(N), 因为每一个结点都会被访问// 空间复杂度O(树的高度)public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;}//时间复杂度O(N)public boolean isBalanced(TreeNode root) {//看返回的是否为正数, 如果是负数说明不平衡return getHeight2(root) >= 0;}// public int getHeight2(TreeNode root) {// if (root == null) {// return 0;// }// int leftHeight = getHeight2(root.left);// int rightHeight = getHeight2(root.right);// if (leftHeight >= 0 && rightHeight >= 0 &&// Math.abs(leftHeight - rightHeight) <= 1) {// //return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;// return Math.max(leftHeight, rightHeight) + 1;// } else {//左子树和右子树的高度差超过了2// return -1;// }// }public int getHeight2(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight2(root.left);if (leftHeight < 0) {return -1;}int rightHeight = getHeight2(root.right);if (rightHeight < 0) {return -1;}if (Math.abs(leftHeight - rightHeight) <= 1) {//return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;return Math.max(leftHeight, rightHeight) + 1;} else {//左子树和右子树的高度差超过了2return -1;}}
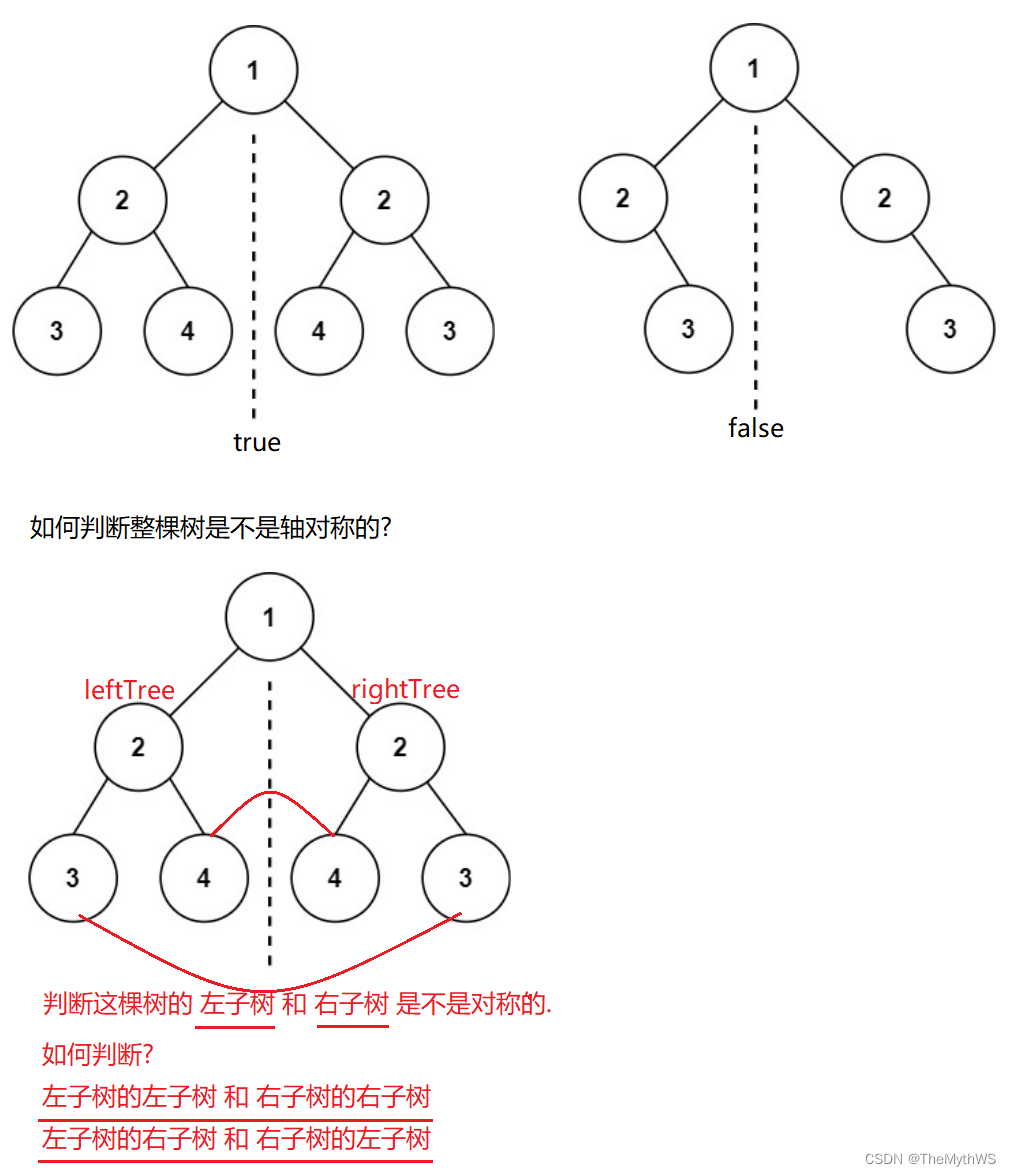
}5. 对称二叉树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) {return true;}return isSymmetricChild(root.left, root.right);}public boolean isSymmetricChild(TreeNode leftTree, TreeNode rightTree) {if (leftTree != null && rightTree == null || leftTree == null && rightTree != null) {return false;}if (leftTree == null && rightTree == null) {return true;}//走到这里说明左子树和右子树都不为空, 就需要先判断值是否一样if (leftTree.val != rightTree.val) {return false;}//走到这里说明左子树和右子树不为空, 且值一样//再判断左子树的左子树和右子树的右子树是否相等, 左子树的右子树和右子树的左子树是否相等.return isSymmetricChild(leftTree.left, rightTree.right) && isSymmetricChild(leftTree.right, rightTree.left);}
}6. 二叉树的构建及遍历。
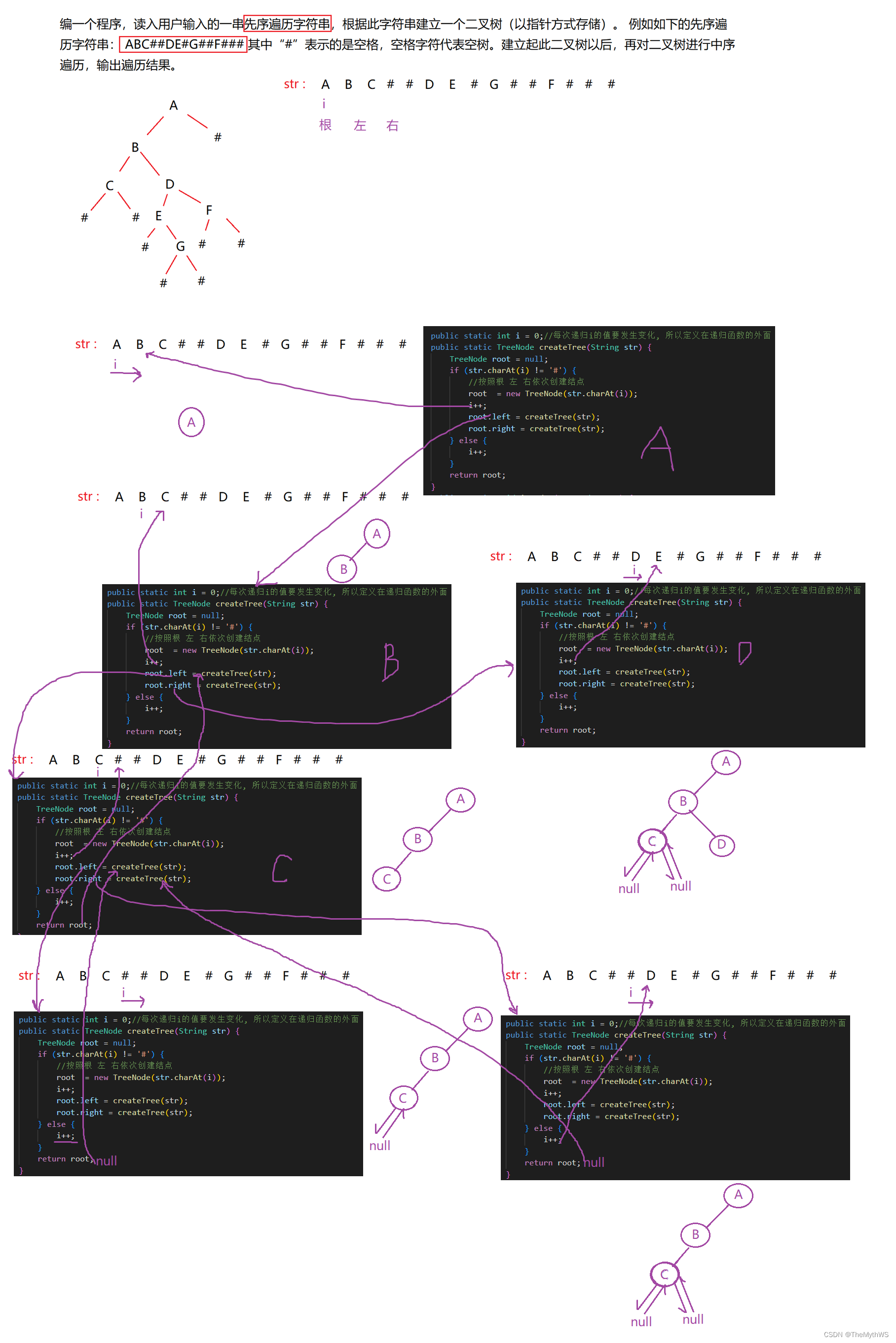
import java.util.Scanner;
class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseString str = in.nextLine();TreeNode root = createTree(str);inOrder(root);}}public static int i = 0;//每次递归i的值要发生变化, 所以定义在递归函数的外面public static TreeNode createTree(String str) {TreeNode root = null;if (str.charAt(i) != '#') {//按照根 左 右依次创建结点root = new TreeNode(str.charAt(i));i++;root.left = createTree(str);root.right = createTree(str);} else {i++;}return root;}public static void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}
}7. 二叉树的层序遍历 。

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if(root == null) {return list;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {//队列不为空, 记录当前的结点个数size(相当于每一层的结点), 然后出队size个结点, 然后添加到集合.int size = queue.size();List<Integer> tmp = new ArrayList<>();while (size != 0) {//出队size个结点TreeNode cur = queue.poll();tmp.add(cur.val);size--;if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}list.add(tmp);}return list;}
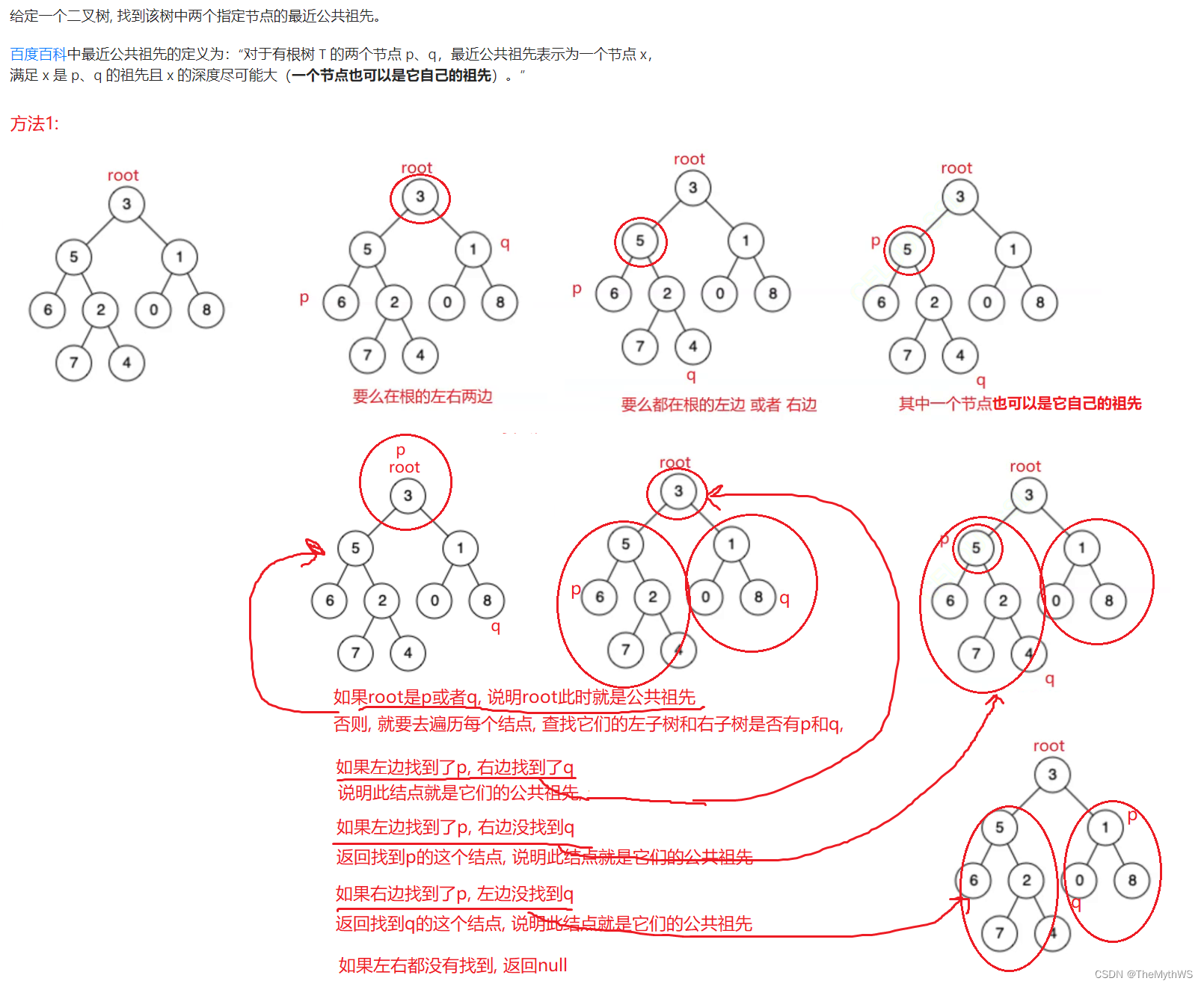
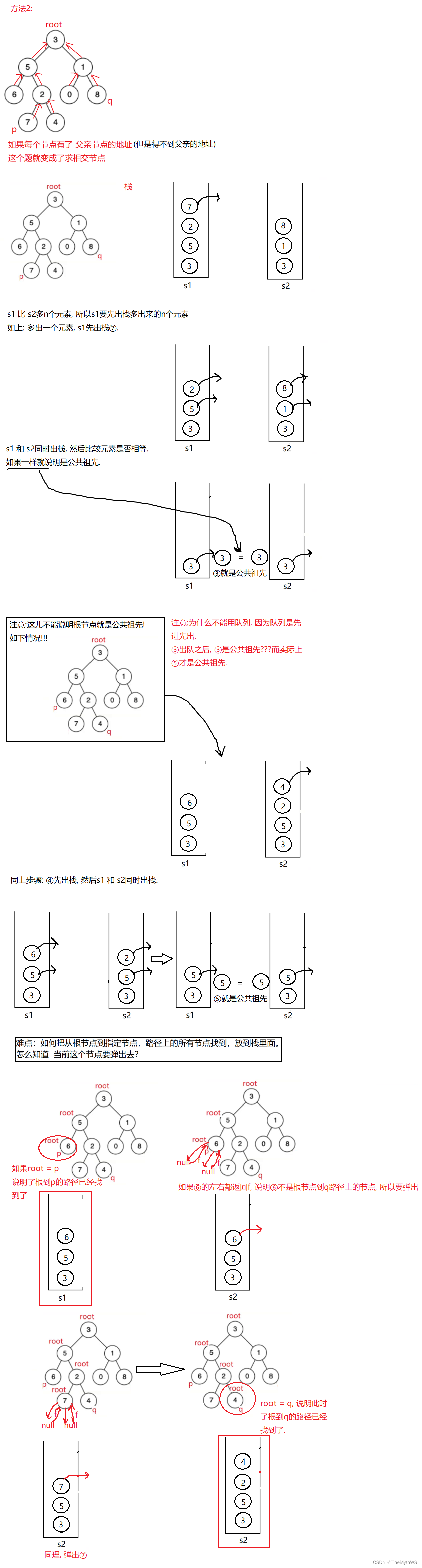
}8. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。
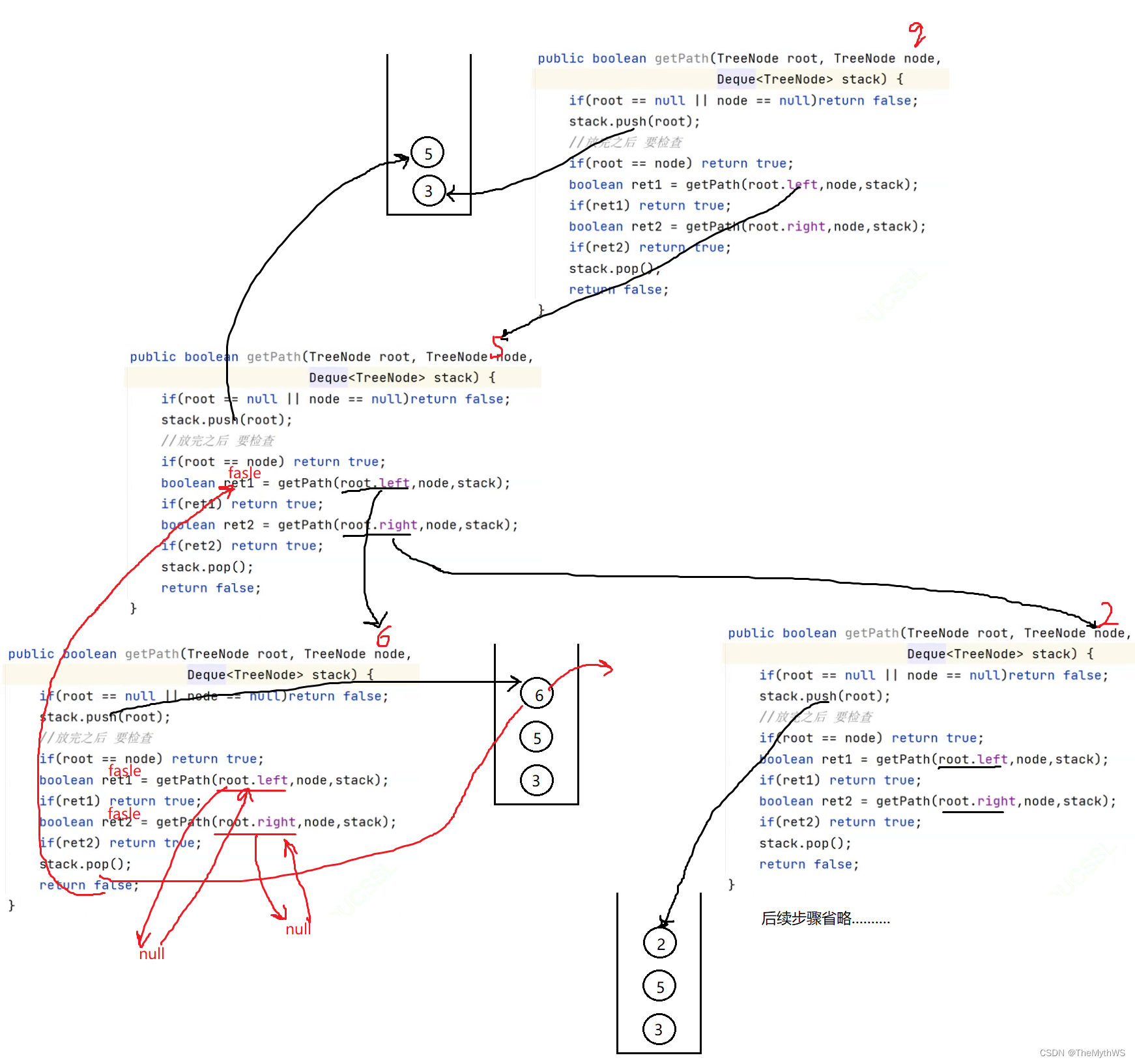
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {//方法1:// public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// if (root == null) {// return null;// }// //先判断根结点是不是其中的一个// if (root == p || root == q) {// return root;// }// //去左子树和右子树找是否有p, q// TreeNode leftRet = lowestCommonAncestor(root.left, p, q);// TreeNode rightRet = lowestCommonAncestor(root.right, p, q);// if (leftRet != null && rightRet != null) {//左子树和右子树都找到了p和q// return root;// } else if (leftRet != null) {//左子树找到的第一个p或者q, 就是公共祖先// return leftRet;// } else if (rightRet != null) {//右子树找到的第一个p或者q, 就是公共祖先// return rightRet;// }// //左子树和右子树都没有找到// return null;// }//方法2:// 找到根节点到指定节点node路径上的所有的节点, 存放到栈中.public boolean getPath(TreeNode root, TreeNode node, Deque<TreeNode> stack) {if (root == null || node == null) {return false;}stack.push(root);//放完之后 要检查if (root == node) {return true;}boolean ret1 = getPath(root.left, node, stack);if (ret1) {//ret1 == truereturn true;}boolean ret2 = getPath(root.right, node, stack);if (ret2) {//ret2 == truereturn true;}stack.pop();return false;}public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//1.两个栈当中 存储好数据Deque<TreeNode> stack1 = new ArrayDeque<>();getPath(root, p, stack1);Deque<TreeNode> stack2 = new ArrayDeque<>();getPath(root, q, stack2);//2.判断栈的大小int size1 = stack1.size();int size2 = stack2.size();//哪个栈的元素多, 就要先出栈多出来的元素if (size1 > size2) {int size = size1 - size2;while (size != 0) {stack1.pop();size--;}} else {int size = size2 - size1;while (size != 0) {stack2.pop();size--;}}//通过上述操作--->栈里面的元素个数是一样的.while (!stack1.isEmpty() && !stack2.isEmpty()) {if (stack1.peek() != stack2.peek()) {stack1.pop();stack2.pop();} else {return stack1.peek();}}return null;}
}9. 根据一棵树的前序遍历与中序遍历构造二叉树。
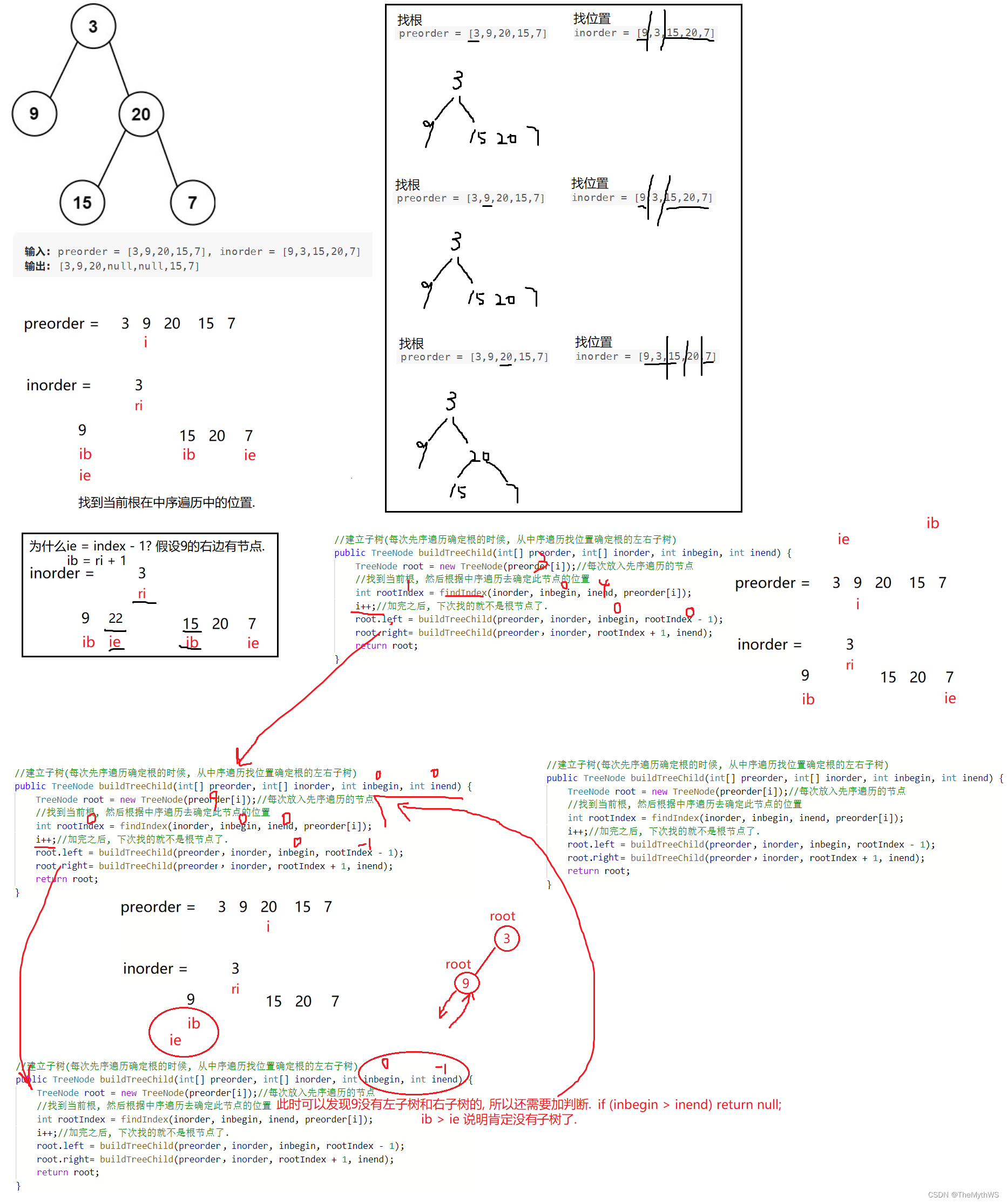
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int i = 0;public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChild(preorder, inorder, 0, inorder.length - 1);}//建立子树(每次先序遍历确定根的时候, 从中序遍历找位置确定根的左右子树)public TreeNode buildTreeChild(int[] preorder, int[] inorder, int inbegin, int inend) {if (inbegin > inend) {//说明没有子树了.return null;}TreeNode root = new TreeNode(preorder[i]);//每次放入先序遍历的节点//找到当前根, 然后根据中序遍历去确定此节点的位置int rootIndex = findIndex(inorder, inbegin, inend, preorder[i]);i++;//加完之后, 下次找的就不是根节点了.root.left = buildTreeChild(preorder, inorder, inbegin, rootIndex - 1);root.right = buildTreeChild(preorder, inorder, rootIndex + 1, inend);return root;}//根据中序遍历, 确定根的位置private int findIndex(int[] inorder, int inbegin, int inend, int key){for (int i = inbegin; i <= inend; i++) {if (inorder[i] == key) {return i;}}return -1;}
}10. 根据一棵树的中序遍历与后序遍历构造二叉树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int i = 0;public TreeNode buildTree(int[] inorder, int[] postorder) {i = postorder.length - 1;//从后往前找.return buildTreeChild(inorder, postorder, 0, inorder.length - 1);}//建立子树(每次后序遍历确定根的时候, 从中序遍历找位置确定根的左右子树)public TreeNode buildTreeChild(int[] inorder, int[] postorder, int inbegin, int inend) {if (inbegin > inend) {//说明没有子树了.return null;}TreeNode root = new TreeNode(postorder[i]);//每次放入后序遍历的节点//找到当前根, 然后根据中序遍历去确定此节点的位置int rootIndex = findIndex(inorder, inbegin, inend, postorder[i]);i--;//减完之后, 下次找的就不是根节点了.//注意:这儿要先建立右树, 因为后序遍历是左 右 根.root.right = buildTreeChild(inorder, postorder, rootIndex + 1, inend);root.left = buildTreeChild(inorder, postorder, inbegin, rootIndex - 1);return root;}//根据中序遍历, 确定根的位置private int findIndex(int[] inorder, int inbegin, int inend, int key) {for (int i = inbegin; i <= inend; i++) {if (inorder[i] == key) {return i;}}return -1;}
}11. 二叉树创建字符串。
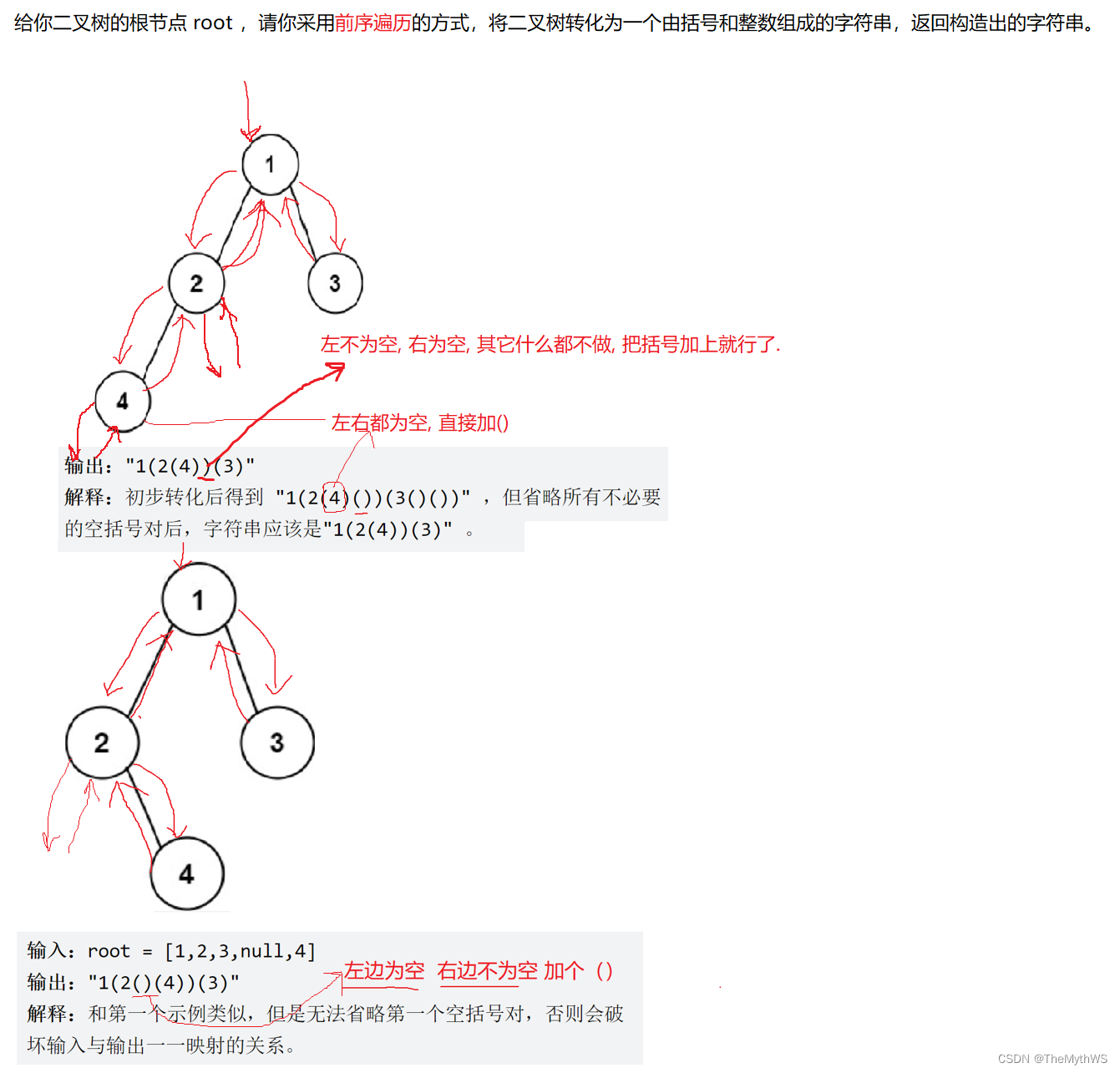
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public String tree2str(TreeNode root) {if (root == null) {return null;}StringBuilder stringBuilder = new StringBuilder();tree2strChild(root, stringBuilder);return stringBuilder.toString();}public void tree2strChild(TreeNode t, StringBuilder stringBuilder) {if (t == null) {return;}stringBuilder.append(t.val);//把根节点先加入if (t.left != null) {//左边不为空stringBuilder.append("(");tree2strChild(t.left, stringBuilder);//递归左边stringBuilder.append(")");} else {//左边为空if (t.right != null) {//右边不为空stringBuilder.append("()");} else {//右边为空return;}}if (t.right == null) {//右边为空return;} else {//右边不为空stringBuilder.append("(");tree2strChild(t.right, stringBuilder);//递归右边stringBuilder.append(")");}}
}12. 二叉树前序非递归遍历实现 。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//递归的写法:/*//不好的写法: 没利用返回值 (遍历思路, 遇到一个打印一个)List<Integer> ret = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {//List<Integer> ret = new ArrayList<>();//这句话不能放在这儿, 因为每次递归ret都是新的值.所以要把ret提到函数外面if(root == null) {return ret;}//System.out.print(root.val+" ");ret.add(root.val);preorderTraversal(root.left);preorderTraversal(root.right);return ret;}*//*//将就的写法:public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret = new ArrayList<>();//这儿放到函数内是因为递归调用的不是本身的函数,不会让ret每次是新的值, 而是另一个函数func.func(root,ret);return ret;}public void func(TreeNode root,List<Integer> ret) {//递归的函数if(root == null) {return;}//System.out.print(root.val+" ");ret.add(root.val);func(root.left,ret);func(root.right,ret);}*///子问题思路// public List<Integer> preorderTraversal(TreeNode root) {// List<Integer> ret = new ArrayList<>();//如果非要写在这儿, 将每次递归的返回值, 加到ret中// if (root == null) {// return ret;// }// ret.add(root.val);// List<Integer> leftTree = preorderTraversal(root.left);// ret.addAll(leftTree);//addAll(Collection<? extends E> c), 尾插c中的元素, 传入的参数是实现了collection接口且泛型类型<=Integer// List<Integer> rightTree = preorderTraversal(root.right);// ret.addAll(rightTree);// return ret;// }//非递归的写法:public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret = new ArrayList<>();if (root == null) {return ret;}TreeNode cur = root;Deque<TreeNode> stack = new ArrayDeque<>();while (cur != null || !stack.isEmpty()) {//如果cur == null && stack == null 说明已经遍历完了.while (cur != null) {stack.push(cur);//System.out.print(cur.val + " ");ret.add(cur.val);cur = cur.left;}//左边为空, 弹出栈顶的元素TreeNode top = stack.pop();cur = top.right;/*如果右边为空, 最外层的while循环也进入不了,但是如果此时栈内还有元素, 也可以进入最外层while循环, 但是不能进入最内层while循环然后弹出栈顶的元素*///如果右边不为空, 循环也可以进入, 将新的元素压栈}return ret;}
}13. 二叉树中序非递归遍历实现。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//递归写法:// public List<Integer> inorderTraversal(TreeNode root) {// List<Integer> ret = new ArrayList<>();//如果非要写在这儿, 将每次递归的返回值, 加到ret中// if (root == null) {// return ret;// }// List<Integer> leftTree = inorderTraversal(root.left);// ret.addAll(leftTree);//addAll(Collection<? extends E> c), 尾插c中的元素, 传入的参数是实现了collection接口且泛型类型<=Integer// ret.add(root.val);// List<Integer> rightTree = inorderTraversal(root.right);// ret.addAll(rightTree);// return ret;// }//非递归写法:public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ret = new ArrayList<>();if (root == null) {return ret;}TreeNode cur = root;Deque<TreeNode> stack = new ArrayDeque<>();while (cur != null || !stack.isEmpty()) {//如果cur == null && stack == null 说明已经遍历完了.while (cur != null) {stack.push(cur);cur = cur.left;}//左边为空, 弹出栈顶的元素TreeNode top = stack.pop();//System.out.print(cur.val + " ");ret.add(top.val);cur = top.right;/*如果右边为空, 最外层的while循环也进入不了,但是如果此时栈内还有元素, 也可以进入最外层while循环, 但是不能进入最内层while循环然后弹出栈顶的元素*///如果右边不为空, 循环也可以进入, 将新的元素压栈}return ret;}
}14. 二叉树后序非递归遍历实现。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//递归实现:// public List<Integer> postorderTraversal(TreeNode root) {// List<Integer> ret = new ArrayList<>();//如果非要写在这儿, 将每次递归的返回值, 加到ret中// if (root == null) {// return ret;// }// List<Integer> leftTree = postorderTraversal(root.left);// ret.addAll(leftTree);//addAll(Collection<? extends E> c), 尾插c中的元素, 传入的参数是实现了collection接口且泛型类型<=Integer// List<Integer> rightTree = postorderTraversal(root.right);// ret.addAll(rightTree);// ret.add(root.val);// return ret;// }//非递归实现:public List<Integer> postorderTraversal(TreeNode root) {List<Integer> ret = new ArrayList<>();if (root == null) {return ret;}TreeNode cur = root;TreeNode prev = null;//这个引用用来记录已经打印过的节点Deque<TreeNode> stack = new ArrayDeque<>();while (cur != null || !stack.isEmpty()) {//如果cur == null && stack == null 说明已经遍历完了.while (cur != null) {stack.push(cur);cur = cur.left;}//左边为空, 查看栈顶的元素TreeNode top = stack.peek();if (top.right == null || top.right == prev) {//如果栈顶元素的右边为空或者栈顶元素的右边已经打印过--->打印 + 弹出栈顶元素//System.out.print(top.val + " ");ret.add(top.val);stack.pop();prev = top;} else {cur = top.right;}//如果右边为空, 最外层的while循环也进入不了,//但是如果此时栈内还有元素, 也可以进入最外层while循环, 但是不能进入最内层while循环//然后查看栈顶的元素, 再判断.//如果右边不为空, 循环也可以进入, 将新的元素压栈}return ret;}
}15.二叉树的深度。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1; }
}相关文章:

【详解二叉树】
🌠作者:TheMythWS. 🎇座右铭:不走心的努力都是在敷衍自己,让自己所做的选择,熠熠发光。 目录 树形结构 概念 树的示意图 树的基本术语 树的表示 树的应用 二叉树(重点) 二叉树的定义 二叉树的五…...
【Amazon】在Amazon EKS集群中安装部署最小化KubeSphere容器平台
文章目录 一、准备工作二、部署 KubeSphere三、访问 KubeSphere 控制台四、安装Amazon EBS CSI 驱动程序4.1 集群IAM角色建立并赋予权限4.2 安装 Helm Kubernetes 包管理器4.3 安装Amazon EBS CSI 驱动程序 五、常见问题六、参考链接 一、准备工作 Kubernetes 版本必须为&…...

ubuntu20.04下安装标注工具CVAT
1 安装docker sudo apt-get update sudo apt-get --no-install-recommends install -y apt-transport-https ca-certificates \curl \gnupg-agent \software-properties-commoncurl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add - sudo add-apt-r…...

pytest-pytest-html测试报告这样做,学完能涨薪3k
在 pytest 中提供了生成html格式测试报告的插件 pytest-html 安装 安装命令如下: pip install pytest-html使用 我们已经知道执行用例的两种方式,pytest.main()执行和命令行执行,而要使用pytest-html生成报告,只需要在执行时加…...
本地运行“李开复”的零一万物 34B 大模型
这篇文章,我们来聊聊如何本地运行最近争议颇多的,李开复带队的国产大模型:零一万物 34B。 写在前面 零一万物的模型争议有很多,不论是在海外的社交媒体平台,还是在国内的知乎和一种科技媒体上,不论是针对…...
Redis-Redis缓存高可用集群
1、Redis集群方案比较 哨兵模式 在redis3.0以前的版本要实现集群一般是借助哨兵sentinel工具来监控master节点的状态,如果master节点异常,则会做主从切换,将某一台slave作为master,哨兵的配置略微复杂,并且性能和高可…...
Django之admin页面样式定制(Simpleui)
好久不见,各位it朋友们! 本篇文章我将向各位介绍Django框架中admin后台页面样式定制的一个插件库,名为Simpleui。 一)简介 SimpleUI是一款简单易用的用户界面(UI)库,旨在帮助开发人员快速构建…...

TypeScript 中的type与interface
TypeScript 中的type与interface 对于 TypeScript,有两种定义类型的方法:type与interface。 人们常常想知道该使用哪一种,而答案并不是一刀切的。这确实取决于具体情况。有时,其中一种比另一种更好,但在许多情况下&a…...
【uniapp】uniapp开发小程序定制uni-collapse(折叠面板)
需求 最近在做小程序,有一个类似折叠面板的ui控件,效果大概是这样 代码 因为项目使用的是uniapp,所以打算去找uniapp的扩展组件,果然给我找到了这个叫uni-collapse的组件(链接:uni-collapse)…...
单片机学习7——定时器/计数器编程
#include<reg52.h>unsigned char a, num; sbit LED1 P1^0;void main() {num0;EA1;ET01;//IT00;//设置TMOD的工作模式TMOD0x01;//给定时器装初值,50000,50ms中断20次,就得到1sTH0(65536-50000)/256;TL0(65536-50000)%256;TR01; // 定时器/计数器启…...
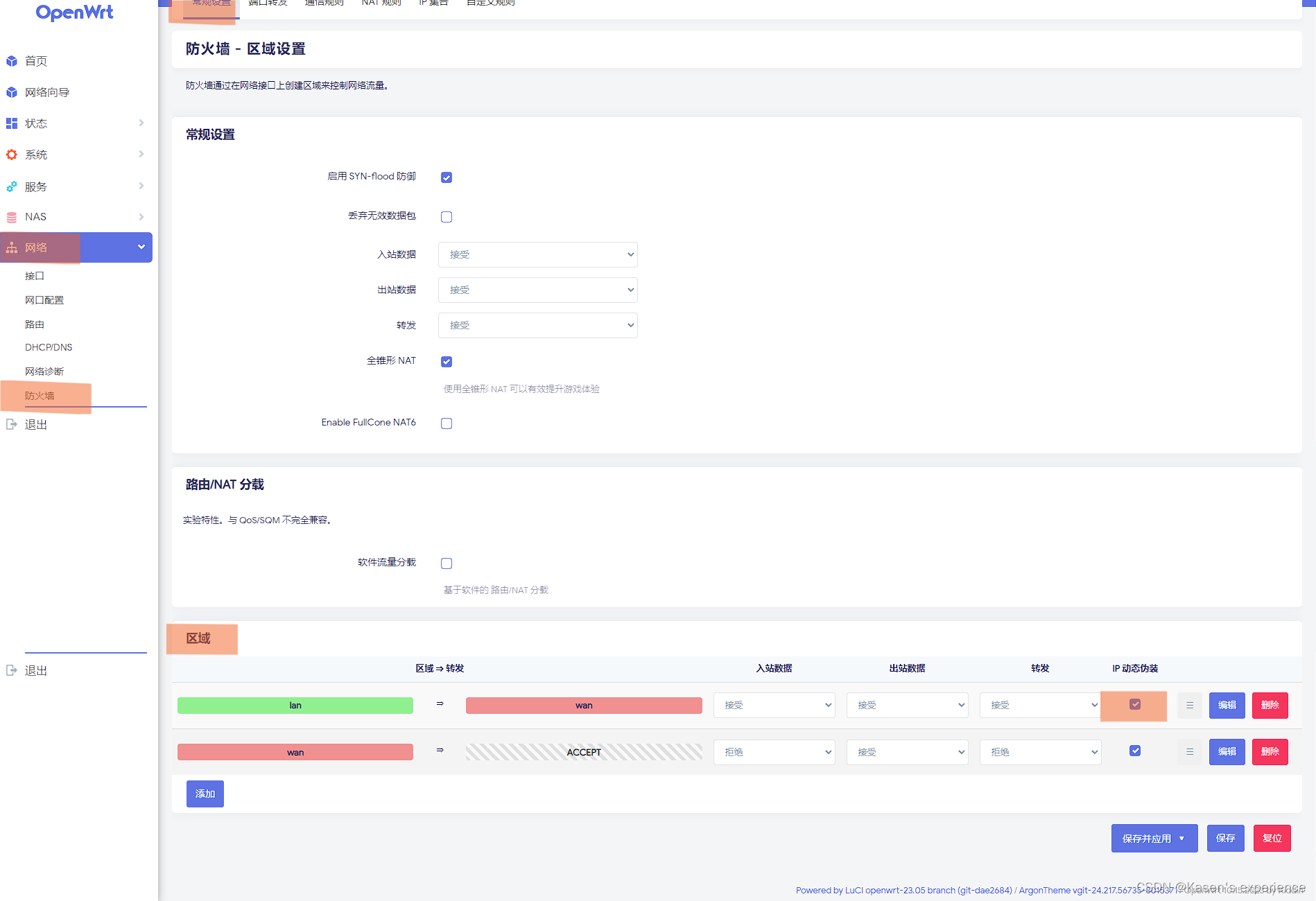
OpenWrt Lan口上网设置
LAN口上网设置 连接上openwrt,我用的 倍控N5105,eth0,看到Openwrt的IP是10.0.0.1 在 网络 -> 网口配置 -> 设置好 WAN 口和 LAN 口 初次使用经常重置 openwrt 所以我设置的是 静态IP模式 - 网络 -> 防火墙 -> 常规设置 ->…...

监控同一局域网内其它主机上网访问信息
1.先取得网关IP 2.安装IPTABLES路由表 sudo apt-get install iptables 3.启用IP转发 sudo sysctl -p 查看配置是否生效 4.配置路由 iptables -t nat -A POSTROUTING -j MASQUERADE 配置成功后,使用sudo iptables-save查看...

DC cut 滤直流滤波器实现
在音频处理中,会无意中产生直流偏置,这个偏置如果通过功放去推喇叭,会对喇叭造成不可逆转的损坏,所以在实际应用中,会通过硬件(添加直流检测模块,如果有 使用继电器切断输出) 、软件(软件直流滤波算法)&…...
uni-app,nvue中text标签文本超出宽度不换行问题解决
复现:思路: 将text标签换为rich-text,并给rich-text增加换行的样式class类名解决:...

和鲸ModelWhale平台与海光人工智能加速卡系列完成适配认证,夯实 AI 应用核心底座
AIGC 浪潮席卷,以大模型为代表的人工智能发展呈现出技术创新快、应用渗透强、国际竞争激烈等特点。创新为本,落地为王,技术的快速发展与大规模训练需求的背后,是对平台化基础设施与 AI 算力的更高要求。在此全球 AI 产业竞争的风口…...
Flutter学习(四)如何取消listview的越界效果
背景 在flutter的开发过程中,ListView是很常见的一个组件,但是,由于ListView的某些自带的体验,导致不太好的用户体验。例如ListView中,滑动到顶部或者底部的时候,再次滑动,会有越界的效果&…...

system.setProperty导致的https血案
system.setProperty导致的https血案 现象排查思考建议 现象 系统外调签名服务突然无法使用,排查发起请求的服务正常,查看日志报recieve fatal alert: protocal_version, 当时大家没有深入研究代码,印象里最近没有动过服务,就网络…...

Python 测试框架 Pytest 的入门
简介 pytest 是一个功能强大而易于使用的 Python 测试框架。它提供了简单的语法和灵活的功能,用于编写和组织测试代码。 1、简单易用:pytest 的语法简洁明了,使得编写测试用例更加直观和易于理解。它使用 assert 语句来验证预期结果&#x…...

【开源】基于Vue.js的数据可视化的智慧河南大屏
项目编号: S 059 ,文末获取源码。 \color{red}{项目编号:S059,文末获取源码。} 项目编号:S059,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、系统展示四、核心代码4.1 数据模块 …...
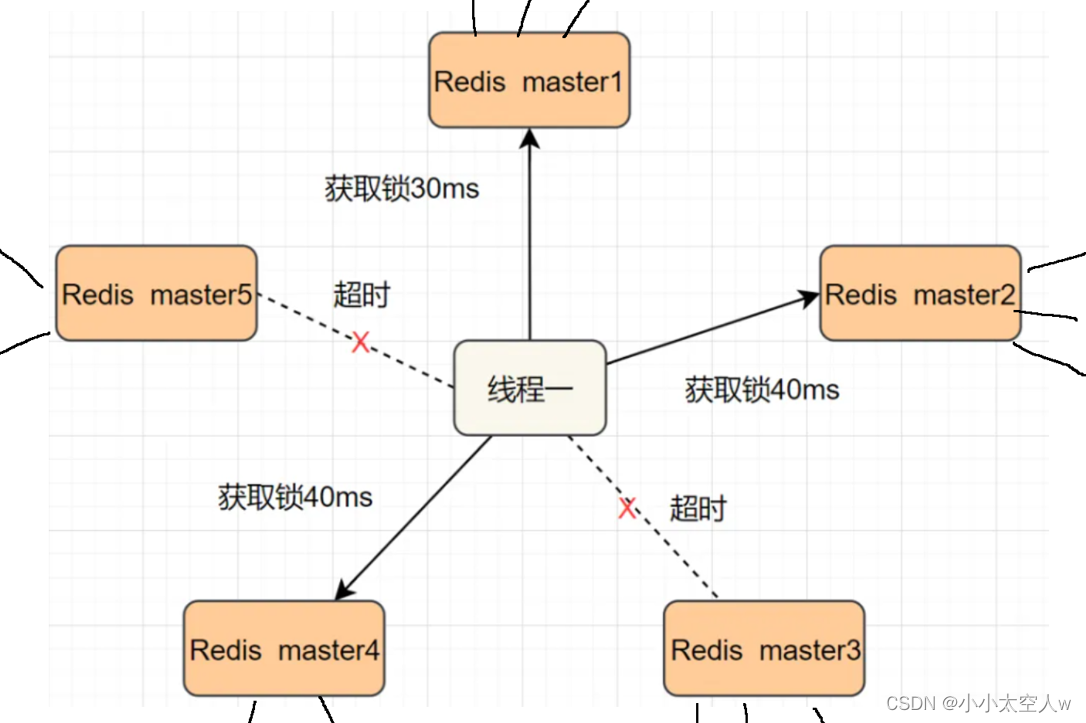
什么是分布式锁?Redis实现分布式锁详解
目录 前言: 分布式系统买票示例 引入redis做分布式锁 引入过期时间 引入校验id 引入lua脚本 过期时间续约问题 redlock算法 小结: 前言: 在分布式系统中,涉及多个主机访问同一块资源,此时就需要锁来做互斥控制…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...