使用Three.js创建导航立方体
什么是导航立方体？
导航立方体是一个交互式的3D控件，它允许用户通过点击和拖动立方体的各个面来改变3D视图的方向。这是一种非常直观的方式，让用户能够轻松地在3D空间中导航。
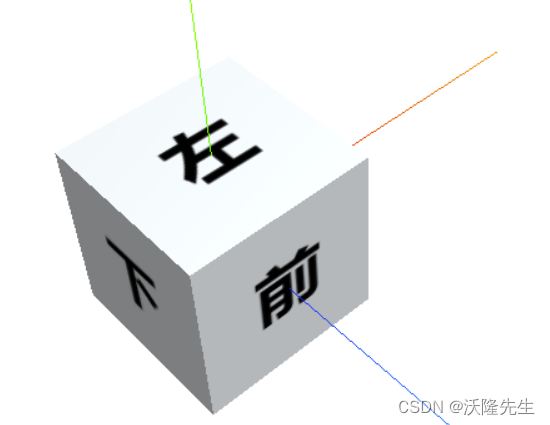
创建导航立方体
下面是一个基本的步骤，说明如何使用Three.js创建一个导航立方体：
// 创建场景var scene = new THREE.Scene();// 创建相机var camera = new THREE.PerspectiveCamera(75, window.innerWidth / window.innerHeight, 0.1, 1000);camera.position.z = 5;// 创建渲染器var renderer = new THREE.WebGLRenderer();renderer.setSize(window.innerWidth, window.innerHeight);renderer.setClearColor(0xffffff); // set to whitedocument.body.appendChild(renderer.domElement);// 创建立方体的几何体var geometry = new THREE.BoxGeometry(1, 1, 1);// 创建立方体的每个面的材质const CANVAS_SIZE = 256;var materials = [];['上', '下', '左', '右',相关文章：
使用Three.js创建导航立方体
什么是导航立方体？ 导航立方体是一个交互式的3D控件，它允许用户通过点击和拖动立方体的各个面来改变3D视图的方向。这是一种非常直观的方式，让用户能够轻松地在3D空间中导航。 创建导航立方体 下面是一个基本的步骤，说明如何使用Three.js创建一个导航立方体： // 创建场景…...
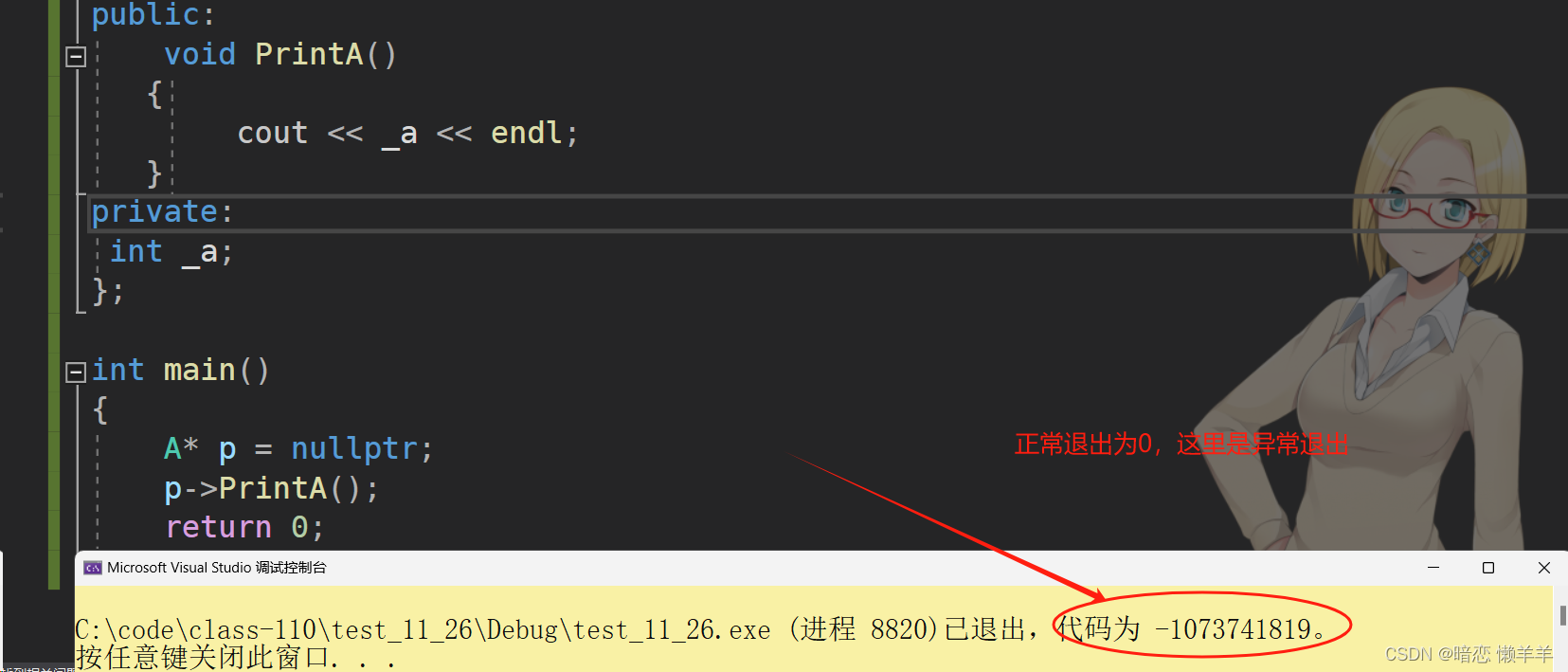
C++初识类和对象
前言 上一期我们介绍了一些C入门的基础知识，本期我们来介绍面向对象。初步认识一下面向对象和面向过程、类、以及封装！ 本期内容介绍 面向过程和面向对象 类的引入 类的定义 类的访问限定符和封装 类的作用域 类的实例化 类对象模型 this指针 一、面向…...
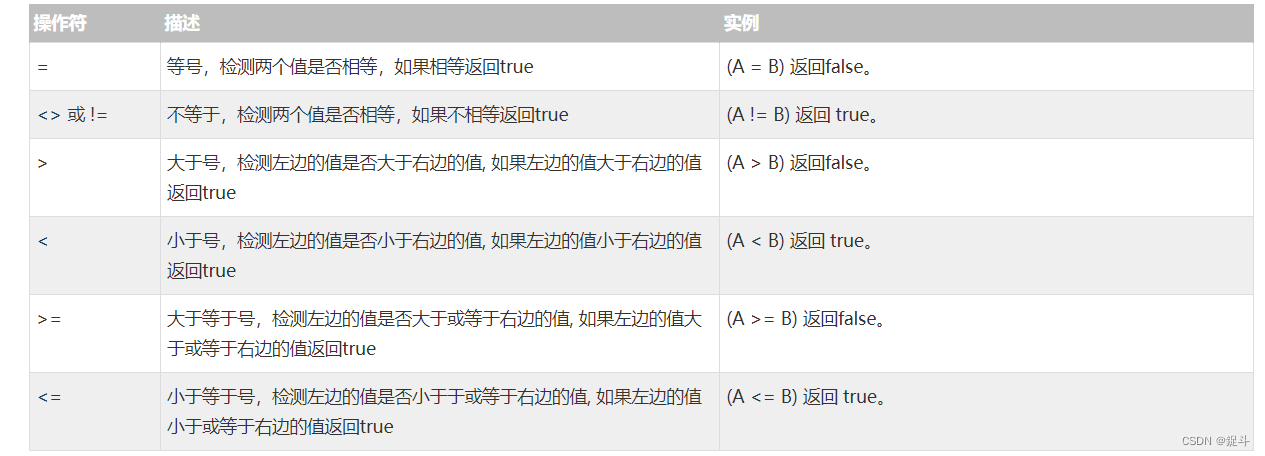
MYSQL where 子句
文章目录 前言MySQL where 子句语法 从命令提示符中读取数据使用PHP脚本读取数据后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏：Mysql 🐱👓博主在前端领域还有很多知识和技术需要掌握，正在不断努力…...
系列十六、Spring IOC容器的扩展点
一、概述 Spring IOC容器的扩展点是指在IOC加载的过程中，如何对即将要创建的bean进行扩展。 二、扩展点 2.1、BeanDefinitionRegistryPostProcessor 2.1.1、概述 BeanDefinitionRegistryPostProcessor是bean定义的后置处理器，在BeanDefinition加载后&a…...
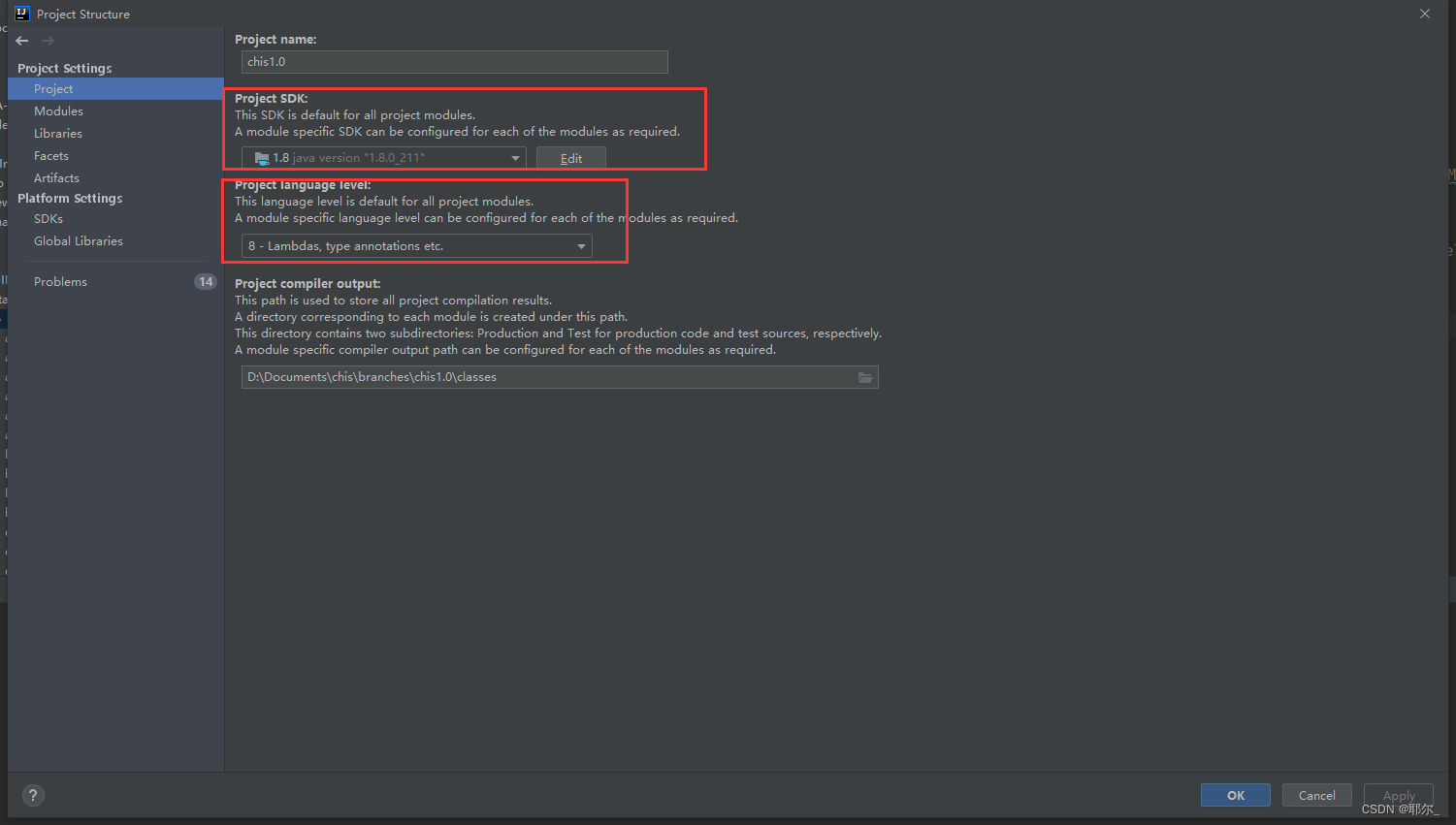
eclipse项目移到idea上部署运行
1.配置web模块 另外，模块这里，也要加上Spring 2.配置Artifact （用于tomcat） 就是从上面配置的web模块，产生的工件 3.添加lib 一般是在web-inf/lib ， 遇到的坑： jdk版本问题，这里…...
支持向量机的算法原理
支持向量机（Support Vector Machine，简称SVM）是机器学习领域中一种常用的分类算法，它基于统计学习理论和结构风险最小化原则，具有很强的理论基础和良好的分类性能。本文将详细介绍支持向量机的算法原理，并解…...
)
gitlab 12升级14(解决各种报错问题)
1.这里是从自己公司的源下载的rpm包，需要换成自己的 2.从12的最后一个版本升级到14的最后一个版本 # 停服务 [rootdocker test]# gitlab-ctl stop puma && gitlab-ctl stop sidekiq && gitlab-ctl stop nginx && gitlab-ctl status# 进入…...
给element plus中动态form-item增加校验的可行方法
element plus中的form组件自带校验机制。在常规使用场景中，表单项是固定的、明确的，且数量不会太多。校验规则的使用也如下： <template><div class"edit-page"><el-form :model"formModel" ref"for…...
C++学习之值传递
c/c中存在三种传值方式，在局部函数中，对这三种传值方式传入的参数进行修改，会得到不同的结果。具体见下例： #include <stdlib.h> #include <stdio.h>static int dummny 10000;// 传值(传过来的是原始值的副本&#…...
网络视频播放卡顿原因分析
一、问题描述 某项目通过拉摄像机rtsp流转rtmp/http-flv/ws-flv的方案，使用户可以在网页中观看摄像机的视频画面。在 观看视频时偶发出现卡顿现象。 二、卡顿现象分析和解决 此问题涉及的原因较多，所以得考虑各环节的问题可能性，并根据现场实…...
Android 相机库CameraView源码解析 (二) : 拍照
1. 前言 这段时间，在使用 natario1/CameraView 来实现带滤镜的预览、拍照、录像功能。 由于CameraView封装的比较到位，在项目前期，的确为我们节省了不少时间。 但随着项目持续深入，对于CameraView的使用进入深水区，逐…...
计算机缺少d3dx9_43.dll怎么办？5个方法快速修复d3dx9_43.dll文件
在计算机使用过程中，我们常常会遇到一些错误提示，其中之一就是“d3dx9_43.dll丢失”。这个问题可能会影响到我们的游戏体验或者软件运行。为了解决这个问题，我查阅了一些资料并尝试了多种方法。在这里，我想分享一下我对d3dx9_43.d…...
2023亚太杯数学建模C题思路分析 - 我国新能源电动汽车的发展趋势
1 赛题 问题C 我国新能源电动汽车的发展趋势 新能源汽车是指以先进技术原理、新技术、新结构的非常规汽车燃料为动力来源( 非常规汽车燃料指汽油、柴油以外的燃料），将先进技术进行汽车动力控制和驱动相结 合的汽车。新能源汽车主要包括四种类型&#x…...
c语言新龟兔赛跑
以下是一个使用C语言编写的新的龟兔赛跑游戏： #include <stdio.h>#include <stdlib.h>#include <time.h>int main() { int distance, turtle_speed, rabbit_speed, turtle_time, rabbit_time, rabbit_lead; srand(time(NULL)); // 随机数种…...
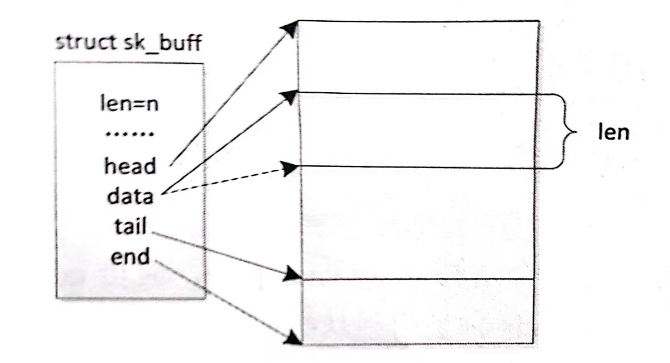
Linux驱动开发——网络设备驱动（理论篇）
目录 一、前言 二、网络层次结构 三、网络设备驱动核心数据结构和函数 一、前言 网络设备驱动是 Linux 的第三大类驱动，也是我们学习的最后一类 Linux 驱动。这里我们首先简单学习一下网络协议层次结构，然后简单讨论 Linux 内核中网络实现的层次结构。…...
simulink仿真
1）系统问题 连续系统，离散系统（采样周期问题） 系统分析问题 2）求解器问题 变步长，定步长，步长时间与采样周期问题、 3）积分器问题 连续积分，离散积分问题ÿ…...
PC端页面进去先出现加载效果
自定义指令v-loading，只需要绑定Boolean即可 v-loading“loading” <el-table :data"list" border style"width: 100%" v-loading"loading"><el-table-column align"center" label"序号" width"5…...
磁盘清理在哪里？学会这4个方法，快速清理内存！
“在使用电脑的过程中，我可能经常会保存一些文件到电脑上，这也导致电脑经常出现内存不足的情况。我想问问磁盘清理在哪里呀？我应该如何打开呢？” 随着使用电脑的时间增长，用户可能经常会遇到磁盘空间不足的情况&#x…...
Error opening terminal: xterm.”的解决方法
主要是看下面这两个变量是否设置正确 $ echo $TERM $ echo $TERMINFO 通常TERM的默认值为xterm-265color, 要查看支持的term，可以ls -al /lib/terminfo/x/ 如果TERM是xterm-265color的话，TERMINFO设置为/usr/lib/terminfo make menuconfig时提示“Err…...
C#常见的设计模式-结构型模式
引言 设计模式是软件工程中用于解决常见问题的可复用解决方案。在C#编程中，常见的设计模式具有广泛的应用。本篇博客将重点介绍C#中常见的结构型设计模式，包括适配器模式、装饰器模式、代理模式、组合模式和享元模式。 目录 引言1. 适配器模式(Adapter …...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 （1）连接查询（JOIN） 内连接（INNER JOIN）：返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
黑马Mybatis
Mybatis 表现层：页面展示 业务层：逻辑处理 持久层：持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
` 方法)
深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出：JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中，随机数的生成看似简单，却隐藏着许多玄机。无论是生成密码、加密密钥，还是创建安全令牌，随机数的质量直接关系到系统的安全性。Jav…...
【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...
Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案，允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现（两者等价），用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例： 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
【HTTP三个基础问题】
面试官您好！HTTP是超文本传输协议，是互联网上客户端和服务器之间传输超文本数据（比如文字、图片、音频、视频等）的核心协议，当前互联网应用最广泛的版本是HTTP1.1，它基于经典的C/S模型，也就是客…...
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中，新增了一个本地验证码接口 /code，使用函数式路由（RouterFunction）和 Hutool 的 Circle…...
HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架，允许使用简单的变成模型跨计算机对大型集群进行分布式处理（1.海量的数据存储 2.海量数据的计算）Hadoop核心组件 hdfs（分布式文件存储系统）&a…...