【青蛙跳台阶问题 —— (三种算法)】
青蛙跳台阶问题 —— (三种算法)
- 一.题目介绍
- 1.1.题目
- 1.2.图示
- 二.解题思路
- 三.题解及其相关算法
- 3.1.递归分治法
- 3.2.动态规划算法(Dynamic Programming)
- 3.3.斐波那契数列法
- 四.注意细节
一.题目介绍
1.1.题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
示例 3:
输入:n = 0
输出:1
提示:
0 <= n <= 100
1.2.图示

二.解题思路
此类求多少种可能性 的题目一般都有递推性质 ,即 f(n)和 f(n-1)…f(1)之间是有联系的。
设跳上 n级台阶有 f(n)种跳法。在所有跳法中,青蛙的最后一步只有两种情况: 跳上1级或 2级台阶。
当为 1级台阶: 剩 n-1个台阶,此情况共有 f(n-1)种跳法;
当为 2级台阶: 剩 n-2个台阶,此情况共有 f(n-2)种跳法。
f(n)为以上两种情况之和,即 f(n)=f(n-1)+f(n-2),以上递推性质为斐波那契数列。本题可转化为求斐波那契数列第 n项的值 ,与斐波那契数列等价,唯一的不同在于起始数字不同。
青蛙跳台阶问题: f(0)=1 , f(1)=1, f(2)=2;
斐波那契数列问题: f(0)=0 , f(1)=1, f(2)=1。
三.题解及其相关算法
斐波那契数列的定义是 f(n + 1) = f(n) + f(n - 1),生成第n项的做法有以下几种:
3.1.递归分治法
递归分治法:
原理: 把 f(n)问题的计算拆分成 f(n-1)和 f(n-2)两个子问题的计算,并递归,以 f(0)和 f(1)为终止条件。
缺点: 大量重复的递归计算,例如 f(n)和 f(n - 1)两者向下递归都需要计算 f(n - 2)的值。
这个程序的时间复杂度为 O(2^n),因为我们需要递归地计算从 1 到 n 的所有整数的和。在输入的楼梯数较大时,程序可能会运行超时。
#include <stdio.h>int climbStairs(int n) {int con=(int)1e9 + 7;if (n == 1) {return 1;}else if (n == 2) {return 2;}else {return climbStairs(n - 1)%con + climbStairs(n - 2)%con;}
}int main() {int n;printf("请输入楼梯的阶数:");scanf("%d", &n);int ways = climbStairs(n);printf("%d 阶楼梯一共有 %d 种跳法。\n", n, ways);return 0;
}
3.2.动态规划算法(Dynamic Programming)
动态规划算法(Dynamic Programming)(记忆化递归法):
动态规划: 是一种用于解决多阶段决策问题的算法,它通过将问题分解为更小的子问题,并通过存储已经解决的子问题的结果来避免重复计算。
原理: 在递归法的基础上,新建一个长度为 n的数组,用于在递归时存储 f(0)至 f(n)的数字值,重复遇到某数字时则直接从数组取用,避免了重复的递归计算。
缺点: 记忆化存储的数组需要使用 O(N)的额外空间。
#define MAX 100
int ClimbStairs(int number)
{int con = (int)1e9 + 7;if (number == 1)return 1;else if (number == 2)return 2;else{int dp[MAX];dp[1] = 1;dp[2] = 2;int i = 0;for (i = 3; i <= number; i++){dp[i] = dp[i - 1] % con + dp[i - 2] % con;}return dp[number];}
}int main() {int n;printf("请输入楼梯的阶数:");scanf("%d", &n);int ways = climbStairs(n);printf("%d 阶楼梯一共有 %d 种跳法。\n", n, ways);return 0;
}

3.3.斐波那契数列法
斐波那契数列法:
原理: 以斐波那契数列性质 f(n + 1) = f(n) + f(n - 1)为转移方程。
从计算效率、空间复杂度上看,斐波那契数列法是本题的最佳解法。
int fbnq(int n)
{int con = (int)1e9 + 7;int first = 0;int second = 1;int tem = 0;while (n--){tem = first + second;first = second % con;second = tem % con;}return first;
}
int ClimbStairs(int n) {return fbnq(n + 1);
}
int main() {int n;printf("请输入楼梯的阶数:");scanf("%d", &n);int ways = ClimbStairs(n);printf("%d 阶楼梯一共有 %d 种跳法。\n", n, ways);return 0;
}

四.注意细节
为什么要模1000000007。
参考:https://link.zhihu.com/?target=https%3A//www.liuchuo.net/archives/645
大数相乘,大数的排列组合等为什么要取模
一、1000000007是一个质数(素数),对质数取余能最大程度避免结果冲突/重复
二、int32位的最大值为2147483647,所以对于int32位来说1000000007足够大。int64位的最大值为2^63-1,用最大值模1000000007的结果求平方,不会在int64中溢出。
所以在大数相乘问题中,因为(a∗b)%c=((a%c)∗(b%c))%c,所以相乘时两边都对1000000007取模,再保存在int64里面不会溢出。
这道题为什么要取模,取模前后的值不就变了吗?
确实:取模前 f(43) = 701408733, f(44) = 1134903170, f(45) = 1836311903, 但是 f(46) > 2147483647结果就溢出了。
取模后 f(43) = 701408733, f(44) = 134903163 , f(45) = 836311896, f(46) = 971215059没有溢出。取模之后能够计算更多的情况,如 f(46)。这道题的测试答案与取模后的结果一致。
总结一下,这道题要模1000000007的根本原因是标准答案取模了1000000007。不过大数情况下为了防止溢出,模1000000007是通用做法,原因见第一点。
相关文章:

【青蛙跳台阶问题 —— (三种算法)】
青蛙跳台阶问题 —— (三种算法) 一.题目介绍1.1.题目1.2.图示 二.解题思路三.题解及其相关算法3.1.递归分治法3.2.动态规划算法(Dynamic Programming)3.3.斐波那契数列法 四.注意细节 一.题目介绍 1.1.题目 一只青蛙一次可以跳上1级台阶&am…...

联想yoga AMD处理器 转接头无法电量外接显示器
第一次买AMD的处理器,当时就是为了yogaAMD这款的接口要比英特尔的接口多,没想到AMD处理器真的问题多。经常蓝屏不说,偶尔还点不亮外接显示器。遇到这种问题,不是什么驱动问题,可能你按照网上各种方法打开设备管理器→显…...
OSG粒子系统与阴影 - 阴影shadow(7)
OSG阴影 在虚拟现实仿真中,为了真实地模拟自然效果,阴影效果是不可缺少的,它对一个场景的真实性是非常重要的。在游戏或仿真中,一个高效的阴影往往能够提供非常强悍的视觉真实感。 osgShadow库 在OSG中专门定义了一个名字空间osg…...
vue3项目中使用富文本编辑器
前言 适配 Vue3 的富文本插件不多,我看了很多插件官网,也有很多写的非常棒的,有UI非常优雅让人耳目一新的,也有功能非常全面的。 如: Quill,简单易用,功能全面。editorjs,UI极其优…...

Java EE 进程线程
JavaEE 进程&线程 文章目录 JavaEE 进程&线程1. 进程1.1 概念1.2 进程管理1.3 PCB (Process Control Block) 2. 线程2.1 概念2.1 线程与进程的区别2.3 创建线程 1. 进程 1.1 概念 什么是进程? 进程是操作系统对一个正在执行的程序的一种抽象 我们可以打开…...

GPT写SQL的模版
表:profit_loss_sum_m_snapshot 计算字段:成本cost_whole求和,收入income_whole求和,收入求和-成本求和,成本目标cost_target求和,收入求和-成本目标求和 条件:日期statis_date在2023-11-01&…...
)
蓝桥杯官网练习题(平均)
问题描述 有一个长度为 n 的数组( n 是 10 的倍数),每个数 ai 都是区间 [0,9] 中的整数。小明发现数组里每种数出现的次数不太平均,而更改第 i 个数的代价为 bi,他想更改若干个数的值使得这 10 种数出现的次数相等…...
【无标题】动手学深度学习_现代神经网络_未完
这里写目录标题 深度学习之前的网络 AlexNetAlexNet得到了竞赛冠军AlexNet架构Alex net更多细节数据增强 VGGNiN知识补充flop暂退法 drop_out 深度学习之前的网络 1、核方法 机器学习 SVM现在还是很广泛的使用,因为对调参的需求不那么大,对调参不太敏感…...

Java王者荣耀
GameFrame 图片 package 王者荣耀;import java.awt.*; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.event.KeyAdapter; import java.awt.event.KeyEvent; import java.io.File; import java.util.ArrayList;import javax.soun…...
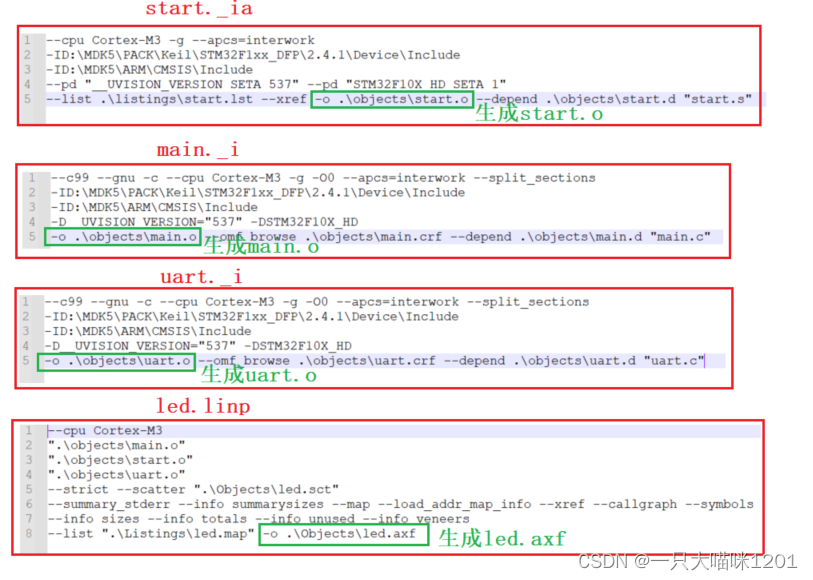
【理解ARM架构】操作寄存器实现UART | 段的概念 | IDE背后的命令
🐱作者:一只大喵咪1201 🐱专栏:《理解ARM架构》 🔥格言:你只管努力,剩下的交给时间! 目录 🍠操作寄存器实现UART🍟UART原理🍟编程 🍠…...

python 左值查找 右值查找
左值查找 在一组数据中查找出 数字x 在这组数据中第一次出现的索引并输出,没有找到则输出-1查找方式:二分查找 数据前提:一组数据要有序一组数据: arr [2, 3, 3, 3, 5, 7, 9, 11, 13, 15, 17]测试: 示例1ÿ…...
MoCo系列翻译与总结(二))
机器学习之自监督学习(四)MoCo系列翻译与总结(二)
MoCo中相关工作的对比分析 去噪自动编码器(Denoising Autoencoder)是一种用于学习数据表示的神经网络模型。它的主要目标是通过去除输入数据中的噪声,学习到输入数据的有用表示,从而提高模型对干净数据的鲁棒性。下面是对去噪自动…...

元宇宙企业3d数字展厅轻松低本搭建更全面、多元、趣味化的展览
对所有企业来说,拥有一个3D线上展厅是互联网营销必不可少的部分,但是3D线上展厅定制周期长费用高,让很多企业公司望而却步,web3d开发公司制作的3D线上企业展厅制作平台备导览地图、语音解说、交互热点、全景漫游、自主行走、链接跳…...
)
华为OD机试真题-开源项目热榜-2023年OD统一考试(C卷)
题目描述: 某个开源社区希望将最近热度比较高的开源项目出一个榜单,推荐给社区里面的开发者。对于每个开源项目,开发者可以进行关注(watch)、收藏(star)、fork、提issue、提交合并请求(MR)等。 数据库里面统计了每个开源项目关注、收藏、fork、issue、MR的数量,开源项目的热…...
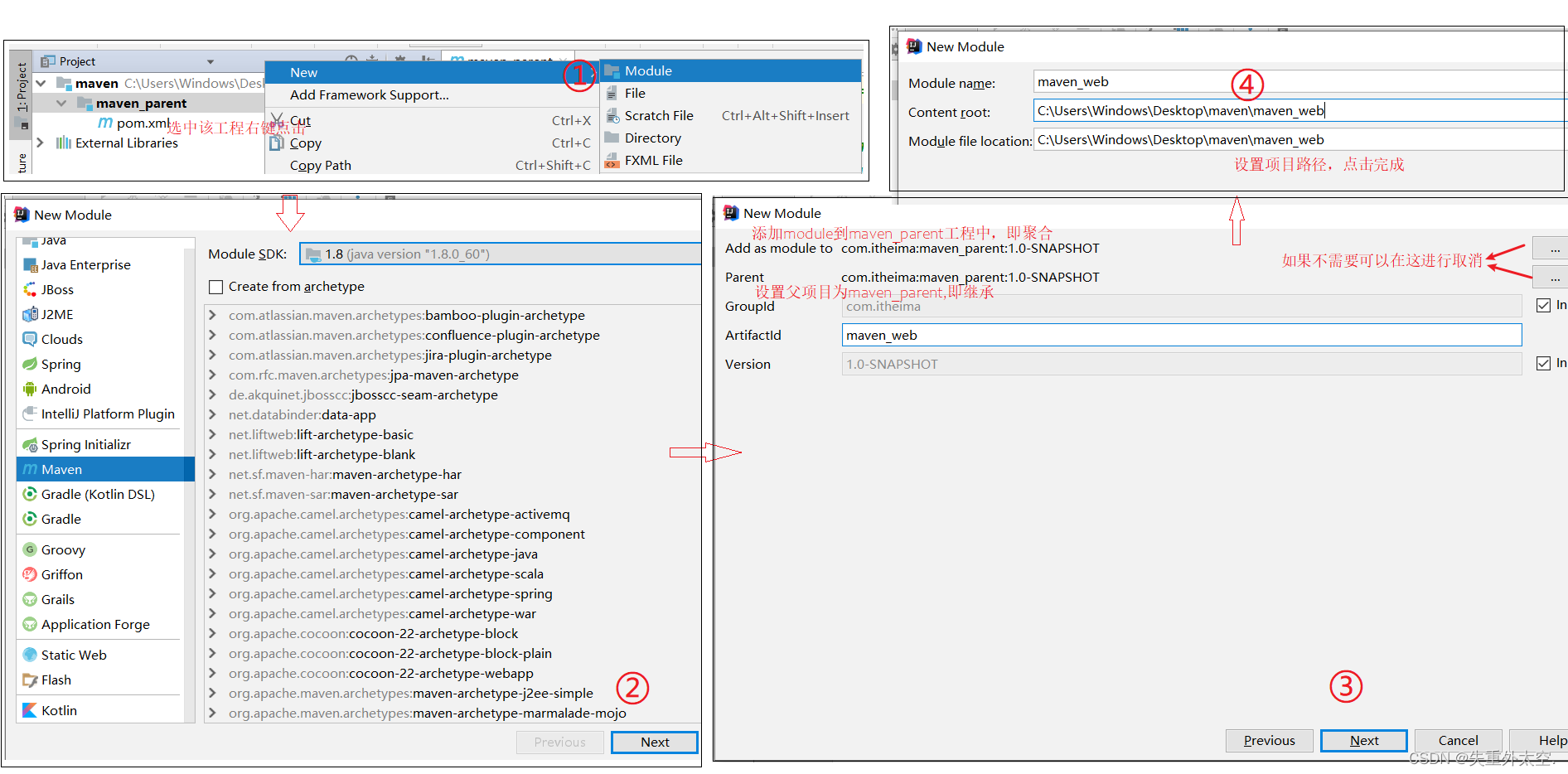
深入探索Maven:优雅构建Java项目的新方式(一)
Maven高级 1,分模块开发1.1 分模块开发设计1.2 分模块开发实现 2,依赖管理2.1 依赖传递与冲突问题2.2 可选依赖和排除依赖方案一:可选依赖方案二:排除依赖 3,聚合和继承3.1 聚合步骤1:创建一个空的maven项目步骤2:将项目的打包方式改为pom步骤…...
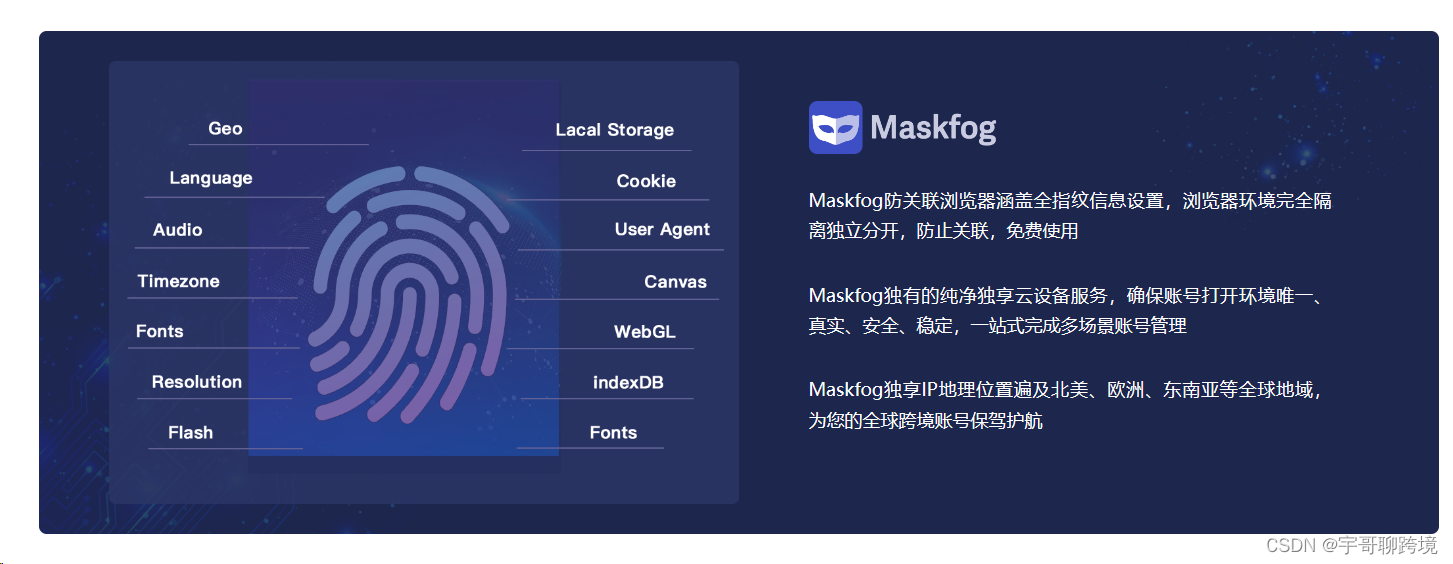
Shopee如何入驻?如何防封?
Shopee作为东南亚领航电商平台,面向东南亚蓝海市场,近年来随着东南亚市场蒸蒸日上,虾皮也吸引了大批量的跨境商家入驻。那么接下来就给想要入驻的虾皮小白一个详细的安全入驻教程。 一、商家如何入驻 虾皮与LAZADA最大的区别就是商家即卖家&…...
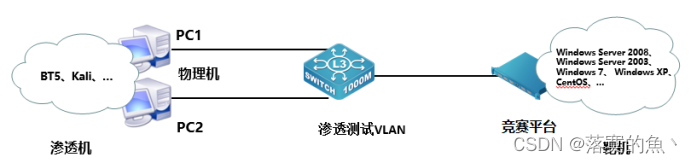
2024年第十六届山东省职业院校技能大赛中职组 “网络安全”赛项竞赛正式卷任务书
2024年第十六届山东省职业院校技能大赛中职组 “网络安全”赛项竞赛正式卷任务书 2024年第十六届山东省职业院校技能大赛中职组 “网络安全”赛项竞赛正式卷A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux&am…...

Python编程基础
Python是一种简单易学的编程语言,广泛应用于Web开发、数据分析、人工智能等领域。无论您是初学者还是有一定编程经验的人士,都可以从Python的基础知识开始建立自己的编程技能。 目录 理论Python语言的发展程序设计语言的分类静态语言与脚本语言的区别 代…...

python类和对象
1.使用对象组织数据 class Student:nameNone #记录名字 stu1Student() #创建对象 stu1.name"abc" #为对象属性赋值2.类的定义和使用 2.1成员方法的定义语法 传参的时候self是透明的,不用管 class Stu:nameNonedef sayHi(self):print(f"你好&#x…...
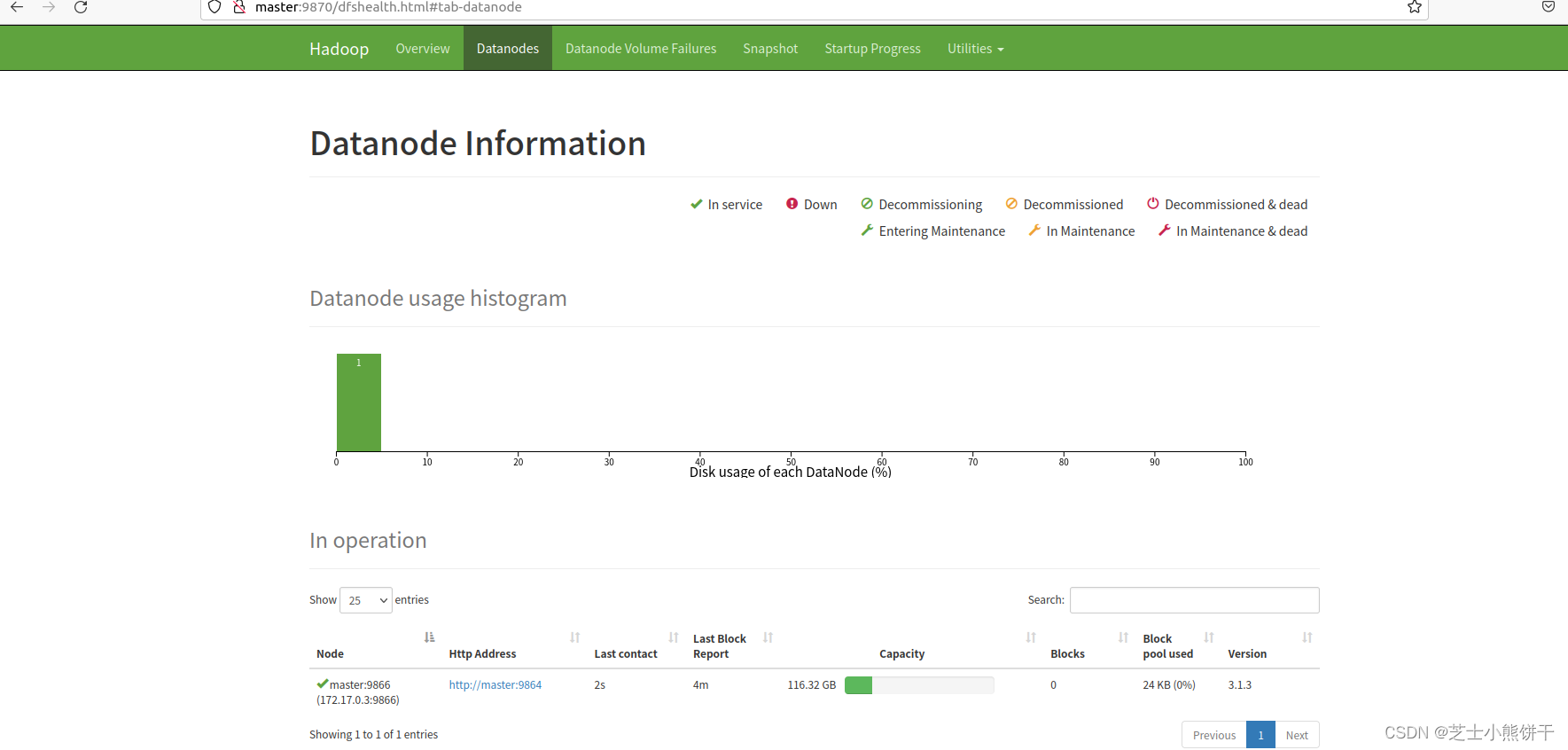
ubuntu操作系统中docker下Hadoop分布式前置环境配置实验
版本: centos7 hadoop 3.1.3 java JDK:1.8 集群规划: masterslave1slave2HDFS NameNode DataNode DataNode SecondryNameNode DataNode YARNNodeManager ResourceManage NodeManager NodeManager 1.docker容器: 把普通用户加入到docker组&am…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

