国内怎么投资黄金,炒黄金有哪些好方法?
随着我国综合实力的不断强大,投资市场的发展也日臻完善,现已成为了国际黄金市场的重要组成部分,人们想要精准判断金市走向,就离不开对我国经济等信息的仔细分析。而想要有效提升盈利概率,人们还需要掌握国内黄金投资的好方法,从而为自己创造更多的盈利优势。
由于黄金提供的是一个全天24小时几乎不间断的交易时间,所以国内炒黄金并不代表着只有在国内的交易盘中进行买卖。根据国际金市的行情特点,国内炒金者会更加具备交易优势,因为行情变化更加丰富的美盘与国内的闲暇时间相重叠,这带给人们更多的市场选择。
所以投资者们可以充分利用这一时间优势来增加自己的炒金成功可能性。比如在行情相对平台的亚盘阶段,以离场观察为主,查看黄金在开盘之后的调整状态,为真正的行情爆发做好盈利铺垫。

同时炒黄金过程中还要密切关注交易账户中的保证金变化,像现货黄金采取的是保证金交易制度,人们可以利用更少的资金投入获得更大的交易规模,但这些因素需要建立在对市场全面分析的基础之上,及时关注保证金变化,有助于发挥这一制度的更多优势,防止出现爆仓风险。
对于炒金者来说,除了要提高操作规范性之外,还应当维持一个良好的交易心态,国际黄金行情丰富多变,机遇与挑战并存二者之间还可以相互转化,所以投资者要始终保持冷静理智,从而准确识别真正的盈利机会。
从近些年的发展历程来看,国内的黄金交易环境不断提升,拥有大量优质的交易平台,为众多炒金者们创造了一个优良的理财环境,投资者要在全面认识市场的基础上,不断提升自己的理财水平,从而有效实现收益增长。
相关文章:

国内怎么投资黄金,炒黄金有哪些好方法?
随着我国综合实力的不断强大,投资市场的发展也日臻完善,现已成为了国际黄金市场的重要组成部分,人们想要精准判断金市走向,就离不开对我国经济等信息的仔细分析。而想要有效提升盈利概率,人们还需要掌握国内黄金投资的…...
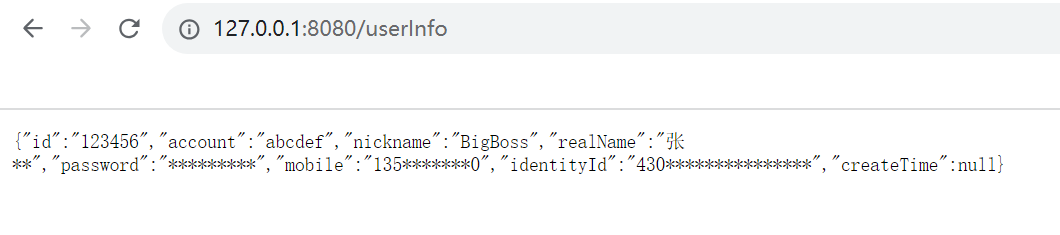
springboot实现数据脱敏
springboot实现数据脱敏 怎么说呢,写着写着发觉 ”这写的什么玩意“ 。 总的来说就是,这篇文章并不能解决数据脱敏问题,但以下链接可以。 SpringBoot中利用自定义注解优雅地实现隐私数据脱敏 然后回到本文,本来是想基于AOP代理&am…...
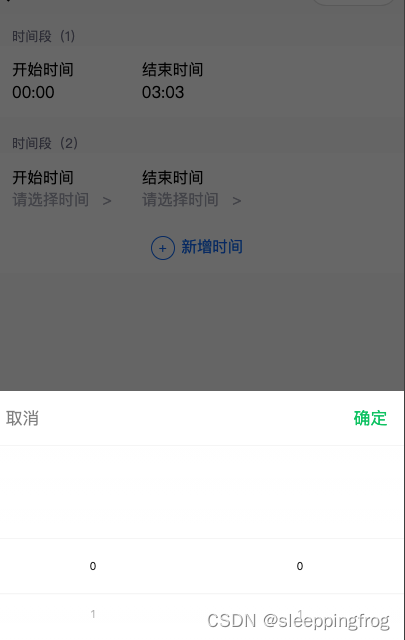
uniapp实现多时间段设置
功能说明: 1 点击新增时间,出现一个默认时间段模板,不能提交 2 点击“新增时间文本”,弹出弹窗,选择时间,不允许开始时间和结束时间同时为00:00, <view class"item_cont"> …...

uni-app - 去除隐藏页面右侧垂直滚动条
全局配置 "globalStyle": { //全局配置 "scrollIndicator":"none", // 不显示滚动条 "app-plus":{ "scrollIndicator":"none" // 在APP平台都不显示滚动条 } }局部配置 "path": "pages/ind…...
)
一次简单的 Http 请求异常处理 (请求的 url 太长, Nginx 直接返回 400, 导致请求服务异常)
1 结论 按照惯例直接说结论。 后台服务 A 有一个 Http 接口, 代码如下: RequestMapping(value "/user", method RequestMethod.GET) public List<UserInfoVo> getUserInfoByUserIds(RequestParam(value "userIds") List<String> userIds…...
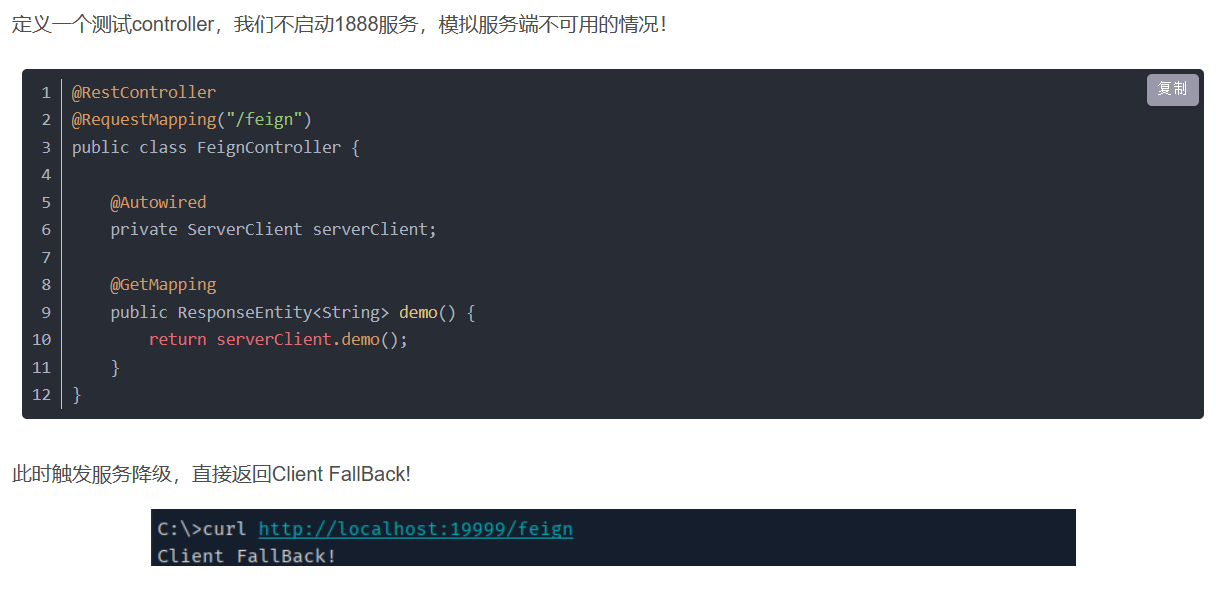
spring Cloud在代码中如何应用,erueka 客户端配置 和 服务端配置,Feign 和 Hystrix做高可用配置
文章目录 Eureka一、erueka 客户端配置二、eureka 服务端配置 三、高可用配置FeignHystrix 通过这篇文章来看看spring Cloud在代码中的具体应用,以及配置和注解; Eureka 一、erueka 客户端配置 1、Eureka 启禁用 eureka.client.enabledtrue 2、Eurek…...

C#8.0中新语法“is {}“的介绍及使用
一、C#7.0及之前is的使用 is操作符检查表达式的结果是否与给定类型兼容,或者(从c# 7.0开始)根据模式测试表达式。有关类型测试is操作符的信息,请参阅类型测试和类型转换操作符文章的is操作符部分。 1、is 模式匹配 从C࿰…...

编译器设计01-入门概述
编译器作用概述 源代码 → 编译器 目标代码 源代码\xrightarrow{\ \ \ 编译器\ \ \ }目标代码 源代码 编译器 目标代码 编译阶段概述 编译处理包括两个阶段:前端处理和后端处理,中间过程生成语法树。 编译处理:源代码 → 语法树 …...

SpringBoot封装Elasticsearch搜索引擎实现全文检索
一、前言 注:本文实现了Java对Elasticseach的分页检索/不分页检索的封装 ES就不用过多介绍了,直接上代码: 二、实现步骤: 创建Store类(与ES字段对应,用于接收ES数据) import com.alibaba.f…...
一些题4)
(C)一些题4
1. 以下叙述中正确的是( )。 A.C程序中的注释只能出现在程序的开始位置和语句的后面 B.C程序书写格式严格,要求行内只能写一个语句 C,C程序书写格式自由,一个语句可以写在多行上 D.用C语言编写的程序只能放在一个程序文件中 2.设有如下程序段 char …...
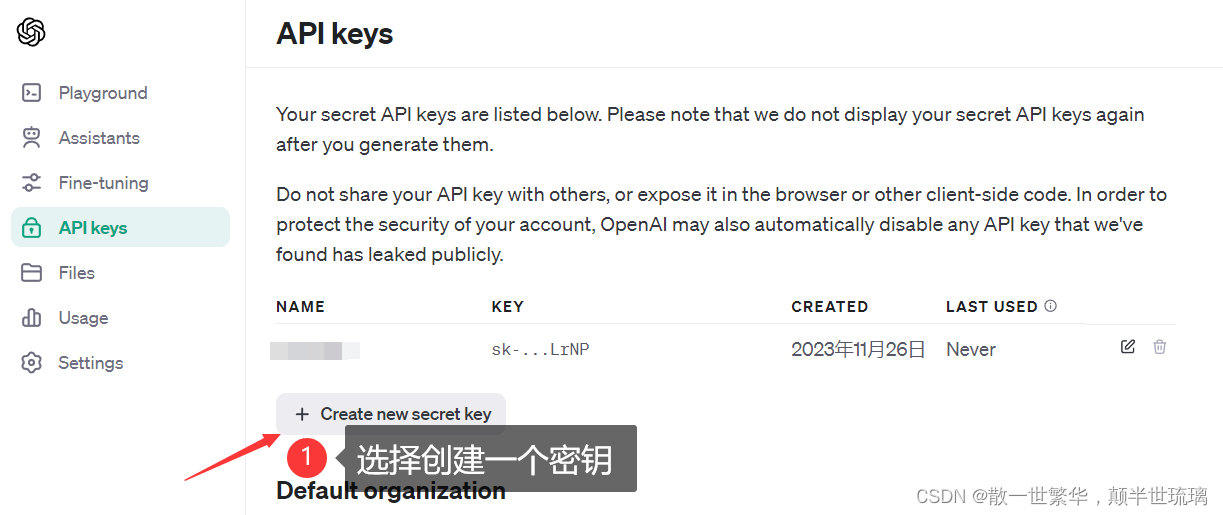
ChatGPT初体验:注册、API Key获取与ChatAPI调用详解
自从2022年10月,ChatGPT诞生以后,实际上已经改变了很多!其火爆程度简直超乎想象,一周的时间用户过百万,两个月的时间用户过亿。 目前ChatGPT4已经把2023年4月以前的人类的知识都学习到了,在软件工程里面&am…...

TCP/IP协议、三次握手、四次挥手
TCP/IP TCP/IP协议分层TCP头部三次握手TCP四次挥手常见问题1、什么是TCP网络分层2、TCP为什么是三次握手,不是两次或者四次?3、TCP为什么是四次挥手,为什么不能是三次挥手将第二次挥手和第三次挥手合并?4、四次挥手时为什么TIME_W…...

Android U 匹配不到APN,无法发起数据建立的问题分析
问题 打开数据开关后,没有data PDN请求发起,因此无法上网。 根据日志确定是没有找到合适的data profile,原因一般有: 1、APN 没有配置 2、APN 类型/网络能力不满足——APN type或bearer 3、APN 配置了但被disable了——APN p…...

如何打造“面向体验”的音视频能力——对话火山引擎王悦
编者按:随着全行业视频化的演进,我们置身于一个充满创新与变革的时代。在这个数字化的浪潮中,视频已经不再只是传递信息的媒介,更是重塑了我们的交互方式和体验感知。作为字节跳动的“能力溢出”,火山引擎正在飞速奔跑…...

什么是NoOps
过去几年,自动化一直在推动整个 IT 行业向前发展。通过自动化某些任务,开发团队可以提高其能力,而无需感受到雇用新团队成员的预算压力。自动化还保证了更高的效率,特别是在操作和维护方面。 传统的软件开发工作流程涉及开发团队…...

Unity - Graphic解析
Gpahic 的作用 Graphic 是 Unity最基础的图形基类。主要负责UGUI的显示部分。 由上图可以看你出我们经常使用的Image,Text,都是继承自Graphic。 Graphic的渲染流程 在Graphic的源码中有以下属性 [NonSerialized] private CanvasRenderer m_CanvasRend…...
哈希思想的应用
目录 1.位图 位图的实现 题目变形一 题目变形二 题目变形三 总结: 2.布隆过滤器 概念 布隆过滤器的实现 3.哈希切割的思想 1.位图 哈希表和位图是数据结构中常用的两种技术。哈希表是一种数据结构,通过哈希函数把数据和位置进行映射,…...

React入门使用 (官方文档向 Part1)
文章目录 React组件:万物皆组件 JSX: 将标签引入 JavaScriptJSX 规则1. 只能返回一个根元素2. 标签必须闭合3. 使用驼峰式命名法给 ~~所有~~ 大部分属性命名!高级提示:使用 JSX 转化器 在 JSX 中通过大括号使用 JavaScript使用引号传递字符串使用大括号&…...
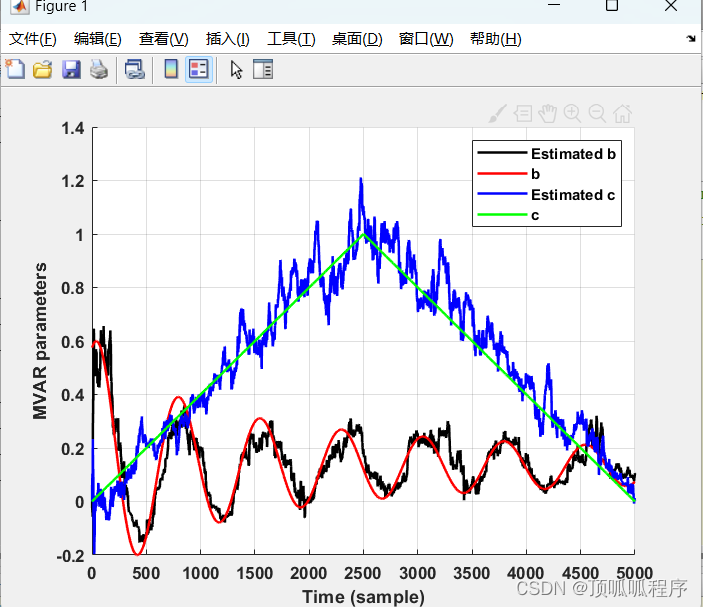
87基于matlab的双卡尔曼滤波算法
基于matlab的双卡尔曼滤波算法。第一步使用了卡尔曼滤波算法,用电池电压来修正SOC,然后将修正后的SOC作为第二个卡尔曼滤波算法的输入,对安时积分法得到的SOC进行修正,最终得到双卡尔曼滤波算法SOC估计值。结合EKF算法和安时积分法…...

Jacobi迭代与SOR迭代求解希尔伯特矩阵
给出线性方程组 Hn*x b,其中系数矩阵Hn为希尔伯特矩阵: 假设 x ∗ (1, 1, . . . , 1)T,b Hnx ∗。若取 n 6,8, 10,分别用 Jacobi 迭代法及 SOR迭代(ω 1, 1:25,1:5)求解,比较计算结果。…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
