Java LeetCode篇-深入了解关于数组的经典解法
🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 轮转数组
1.1 使用移位的方式
1.2 使用三次数组逆转法
2.0 消失的数字
2.1 使用相减法
2.2 使用异或的方式
3.0 合并两个有序数组
3.1 使用三指针方式
3.2 使用合并排序方式
4.0 删除有序数组中的重复项
4.1 使用双指针方式
5.0 移除元素
5.1 使用双指针方式
6.0 杨辉三角
6.1 使用二维数组的方式
1.0 轮转数组
题目:
给定一个整数数组
nums,将数组中的元素向右轮转k个位置,其中k是非负数。示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
1.1 使用移位的方式
先创建一个新的数组来记录需要进行右轮转的元素,然后将数组前面剩余的元素进行遍历 "移" 到后面,即覆盖。如例题1:先将 [5,6,7] 这 k 个元素使用新的数组来暂时存放,接着将 [1,2,3,4] 从后往前遍历,即将 4 移到原来 7 的位置,3 移到 原来 6 的位置,2 移到原来 5 的位置......即 nums[nums.length - i ] = nums[ nums.length - k - i ] ,i 从 1 开始直到 i == nums.length - k 时,则结束循环。最后,将需要轮转的元素进行数组 temp[] 下标一个个对应赋值到 nums[] 数组中即可。
代码如下:
public static void rotate(int[] nums,int k) {if(nums.length == 1 || nums.length == 0) {return;}k %= nums.length;int[] temp = new int[k];System.arraycopy(nums,nums.length - k, temp, 0,k);System.arraycopy(nums,0,nums,k,nums.length - k);for(int i = 0;i < temp.length ; i++) {nums[i] = temp[i];}}这里使用了相关的 API ,总体上来说思路是一样的。一般来说,这种算法时间复杂度会较高。
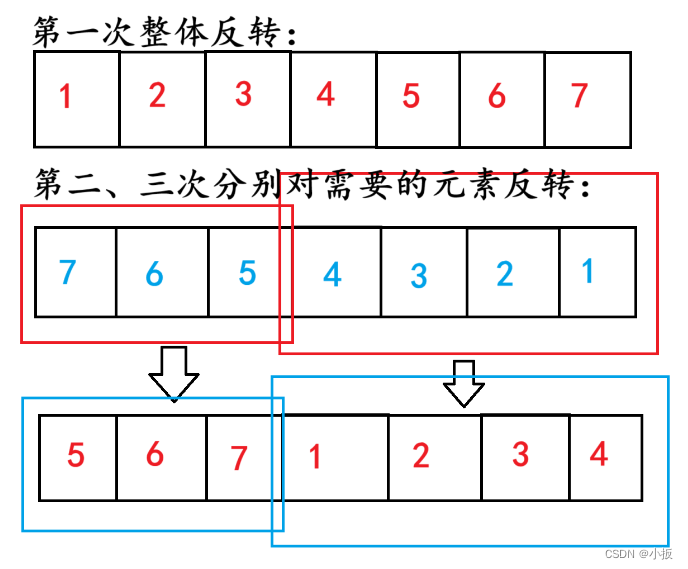
1.2 使用三次数组逆转法
使用三次逆转法,让数组旋转k次
1. 整体逆置
2. 逆转子数组[0, k - 1]
3. 逆转子数组[k, size - 1]
代码如下:
public static void fun(int[] arr, int k) {k %= arr.length;rotate(arr,0,arr.length - 1);rotate(arr,0,k-1);rotate(arr,k, arr.length-1);}public static void rotate(int[] arr,int left, int right) {while (left < right) {int temp = arr[left];arr[left] = arr[right];arr[right] = temp;left++;right--;}}流程图如下:
2.0 消失的数字
题目:
数组
nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在 O(n) 时间内完成吗?示例 1:
输入:[3,0,1] 输出:2示例 2:
输入:[9,6,4,2,3,5,7,0,1] 输出:8
2.1 使用相减法
定义 int sum ,然后遍历 0 到 n 的所有整数都加起来,接着再跟将 nums 的所以数字加起来进行比较,两者相减即可得出 nums 数组中 "消失的数字" 。如例题:numsSum = 3 + 0 + 1 , nSum = 0 + 1 + 2 + 3,再接着 nSum - numsSum == 2 ,两者相减即可得到消失的数字为: 2 。
代码如下:
public static int disappearing1(int[] arr) {int sum1 = 0;int sum2 = 0;for (int i = 0; i < arr.length; i++) {sum1 += i;sum2 += arr[i];}return (sum1 += arr.length) - sum2;}缺陷:如果数组中元素比较多,相加完成之后容易溢出。
2.2 使用异或的方式
采用异或的方式解决,因为两个相同的数字异或的结果是 0,因此:将 0~N 之间的数字,与数组中的每个数字异或,最终的结果就是丢失的数字。
代码如下:
public static int disappearing(int[] arr) {int data = 0;for (int i = 0; i < arr.length; i++) {data ^= arr[i];data ^= i;}data ^= arr.length;return data;}分析:可以将将其理解为 “消消乐” ,即若两个数相同就抵消为 0 ,那么现在目前有两个袋子,一个袋子装满了 0 到 n 张卡片,其中每一种只有一片,也就是说,该袋子里面就有 n + 1 张卡片,在另一个袋子里面装有 0 到 n 张中缺少了一张卡片,即该袋子中有 n 张卡片,接着进行每一次将分别从两个袋子拿出不同的卡片进行对比,如果相同的话则抵消掉了,不相同的话,得保存起来。就这样一直对比下去,最终会发现留下来的就是另一个袋子所缺少的卡片了。
3.0 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组
nums1和nums2,另有两个整数m和n,分别表示nums1和nums2中的元素数目。请你 合并
nums2到nums1中,使合并后的数组同样按 非递减顺序 排列。示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
3.1 使用三指针方式
定义三个指针分别为:i 指向 nums1 中的最后一个有效元素,j 指向 nums2 中最后一个有效元素,k 指向 nums1 中最后一个索引位置。接着 nums[i] 与 nums[j] 进行比较大小,得出较大的元素就放到 nums[k] 中,以此类推,直到 i < 0 或者 j < 0 时,则循环停止。最后来判断,若 i > 0 ,本来剩余的元素就在 nums1 中,则不用再继续下去了,任务结束了;若 j > 0 ,需要将 nums2 中的元素进行遍历拷贝到 nums1 中。
代码如下:
public void merge(int[] nums1, int m, int[] nums2, int n) {int k = nums1.length - 1;int i = m - 1;int j = n - 1;while(i >= 0 && j >= 0) {if(nums1[i] > nums2[j]) {nums1[k] = nums1[i];k--;i--;}else if(nums1[i] <= nums2[j]) {nums1[k] = nums2[j];k--;j--;}}if(j >= 0) {System.arraycopy(nums2,0,nums1,0,j+1);}}
3.2 使用合并排序方式
这个思路很简单,可以直接将 nums2 中的元素拷贝到 nums1 中,然后直接排序即可。这里就不过多赘述了。
4.0 删除有序数组中的重复项
题目:
给你一个 非严格递增排列 的数组
nums,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回nums中唯一元素的个数。示例 1:
输入:nums = [1,1,2] 输出:2, nums = [1,2,_] 解释:函数应该返回新的长度 2,并且原数组 nums 的前两个元素被修改为 1, 2。不需要考虑数组中超出新长度后面的元素。示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4] 输出:5, nums = [0,1,2,3,4] 解释:函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。不需要考虑数组中超出新长度后面的元素。
4.1 使用双指针方式
先定义两个指针分别指向,一个指针: i = 0 ,一开始时指向数组中第一个元素;另一个指针:j = 1。分两种情况来解决,第一种情况是,当 nums[i] == nums[j] 时,继续让 j 走下去,直到 j == nums.length 时,则结束循环;第二种情况是,当 nums[i] != nums[j] 时,让 nums[i + 1] = nums[j] ,i++,j++ ,同样直到 j == nums.length 时,则结束循环。最后返回 i+1 即可。
代码如下:
public int removeDuplicates(int[] nums) {int i = 0;int j = i + 1;while (j < nums.length) {if (nums[i] == nums[j]) {j++;} else if (nums[i] != nums[j]) {nums[i+1] = nums[j];i++;j++;}}return i + 1;}
5.0 移除元素
题目:
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用
O(1)额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3 输出:2, nums = [2,2] 解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2 输出:5, nums = [0,1,3,0,4] 解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
5.1 使用双指针方式
先定义两个指针,对于 left 这个指针来说,一开始指向数组下标为 0 ;对于 right 这个指针来说,一开始指向数组下标也为 0 处,然后 rigth 一直 right++ 自加,在这个过程中,需要先判断,若 nums[right] != val 时,则需要将这个值拷贝到 nums[left] 中 ,left++ ,right++ ;若 nums[right] == val 时,right++ 即可,直到 right == nums.length 时,则结束循环。
代码如下:
public int removeElement(int[] nums, int val) {int n = nums.length;int left = 0;for (int i = 0; i < n; i++) {if (nums[i] != val) {nums[left] = nums[i];left++;}}return left;}
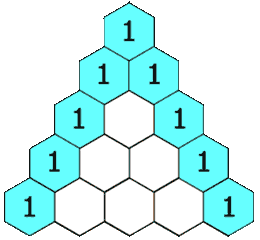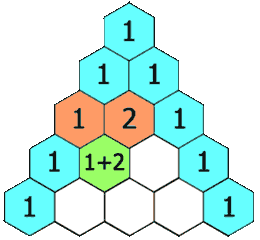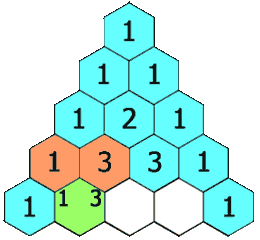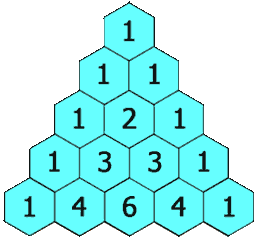
6.0 杨辉三角
题目:
给定一个非负整数
numRows,生成「杨辉三角」的前numRows行。在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2:
输入: numRows = 1 输出: [[1]]
6.1 使用二维数组的方式
可以把这个问题看成是一个二维数组,外层循环为 k 行数(层数),内层为 l 列数。当 l == 0 或者 k == l 时,该二维数组中存放的是 1 ;其他情况则为当前的数值为:上一层行数同一列的 data1 + 上一层行数少一列的 data2 。
代码如下:
public List<List<Integer>> generate(int numRows) {List<List<Integer>> i = new ArrayList<>();for (int k = 0; k < numRows; k++) {List<Integer> j = new ArrayList<>();for (int l = 0; l <= k ; l++) {if ( l == 0 || k == l) {j.add(1);} else {j.add(i.get(k-1).get(l) + i.get(k-1).get(l-1));}}i.add(j);}return i;}需要注意的是,实现集合来实现,而不是数组。
需要了解相关集合的内容可以点击该链接:进阶JAVA篇-深入了解 List 系列集合-CSDN博客
相关文章:
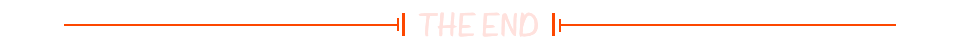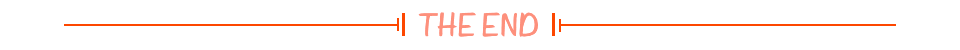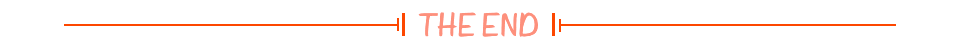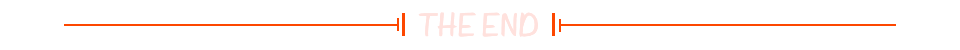
Java LeetCode篇-深入了解关于数组的经典解法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 轮转数组 1.1 使用移位的方式 1.2 使用三次数组逆转法 2.0 消失的数字 2.1 使用相减法 2.2 使用异或的方式 3.0 合并两个有序数组 3.1 使用三指针方式 3.2 使用合…...
- 无重复字符的最长子串)
LeeCode前端算法基础100题(4)- 无重复字符的最长子串
一、问题详情: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s "bbbbb…...

Axios简单使用与配置安装-Vue
安装Axios npm i axios main.js 导入 import Axios from axios Vue.prototype.$axios Axios简单发送请求 get getTest() {this.$axios({method: GET,url: https://apis.jxcxin.cn/api/title?urlhttps://apis.jxcxin.cn/}).then(res > {//请求成功回调console.log(res)}…...
【初始前后端交互+原生Ajax+Fetch+axios+同源策略+解决跨域】
初始前后端交互原生AjaxFetchaxios同源策略解决跨域 1 初识前后端交互2 原生Ajax2.1 Ajax基础2.2 Ajax案例2.3 ajax请求方式 3 Fetch3.1 fetch基础3.2 fetch案例 4 axios4.1 axios基础4.2 axios使用4.2.1 axios拦截器4.2.2 axios中断器 5 同源策略6 解决跨域6.1 jsonp6.2 其他技…...
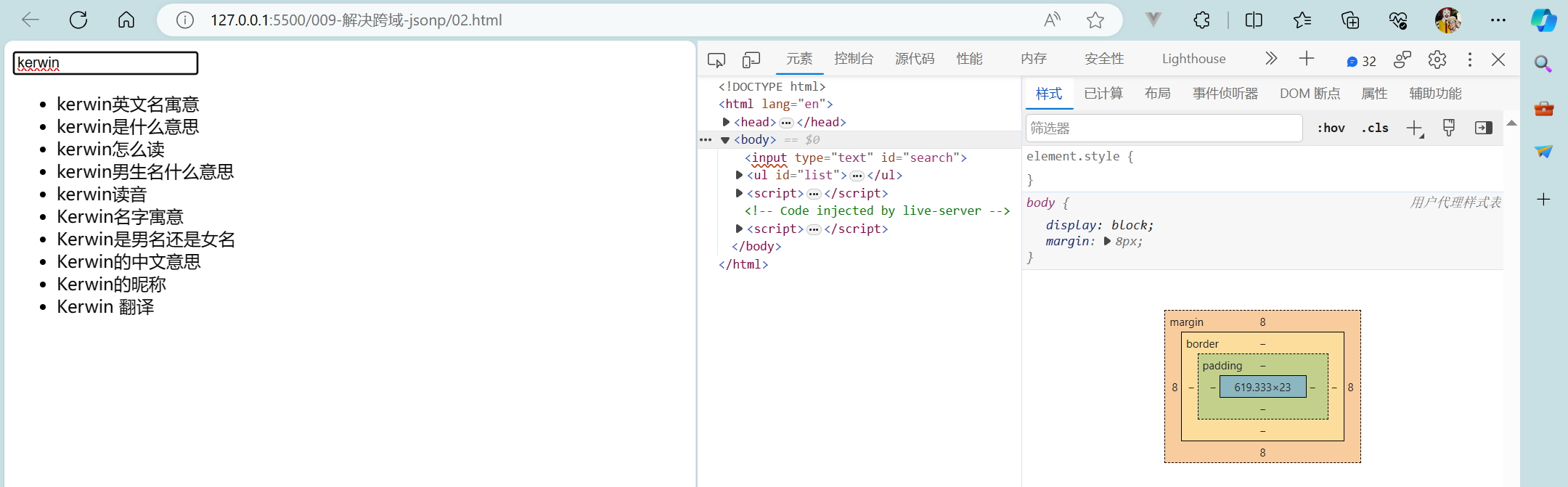
C语言--每日选择题--Day24
第一题 1. 在C语言中,非法的八进制是( ) A:018 B:016 C:017 D:0257 答案及解析 A 八进制是0~7的数字,所以A错误 第二题 2. fun((exp1,exp2),(exp3,exp4,exp5))有几…...
记一次简单的PHP反序列化字符串溢出
今天朋友给的一道题,让我看看,来源不知,随手记一下 <?php // where is flag error_reporting(0); class NFCTF{ public $ming,$id,$payload,$nothing;function __construct($iii){$this->ming$ii…...

找工作面试技巧
问题描述:找工作时,不知道如何回答问题怎么办。 问题解决:可以尝试使用STAT原则来回答问题。具体如下。 "STAR" 原则是一种常用于回答面试问题的方法,特别是在描述个人经验、解决问题或展示技能和能力时。"STAR&q…...
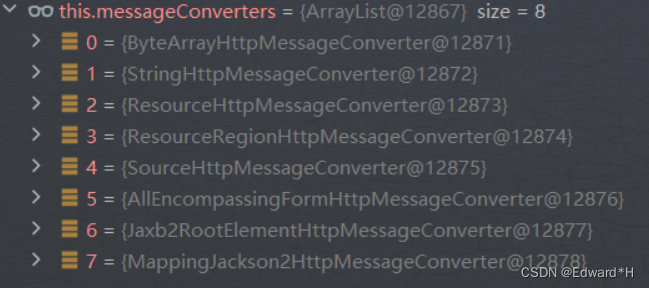
Jackson无缝替换Fastjson
目录 文章目录 一,Fastjson到Jackson的替换方案方案代码序列化反序列化通过key获取某种类型的值类型替换 二,Springboot工程中序列化的使用场景三,SpringMVC框架中的Http消息转换器1,原理:2,自定义消息转换…...
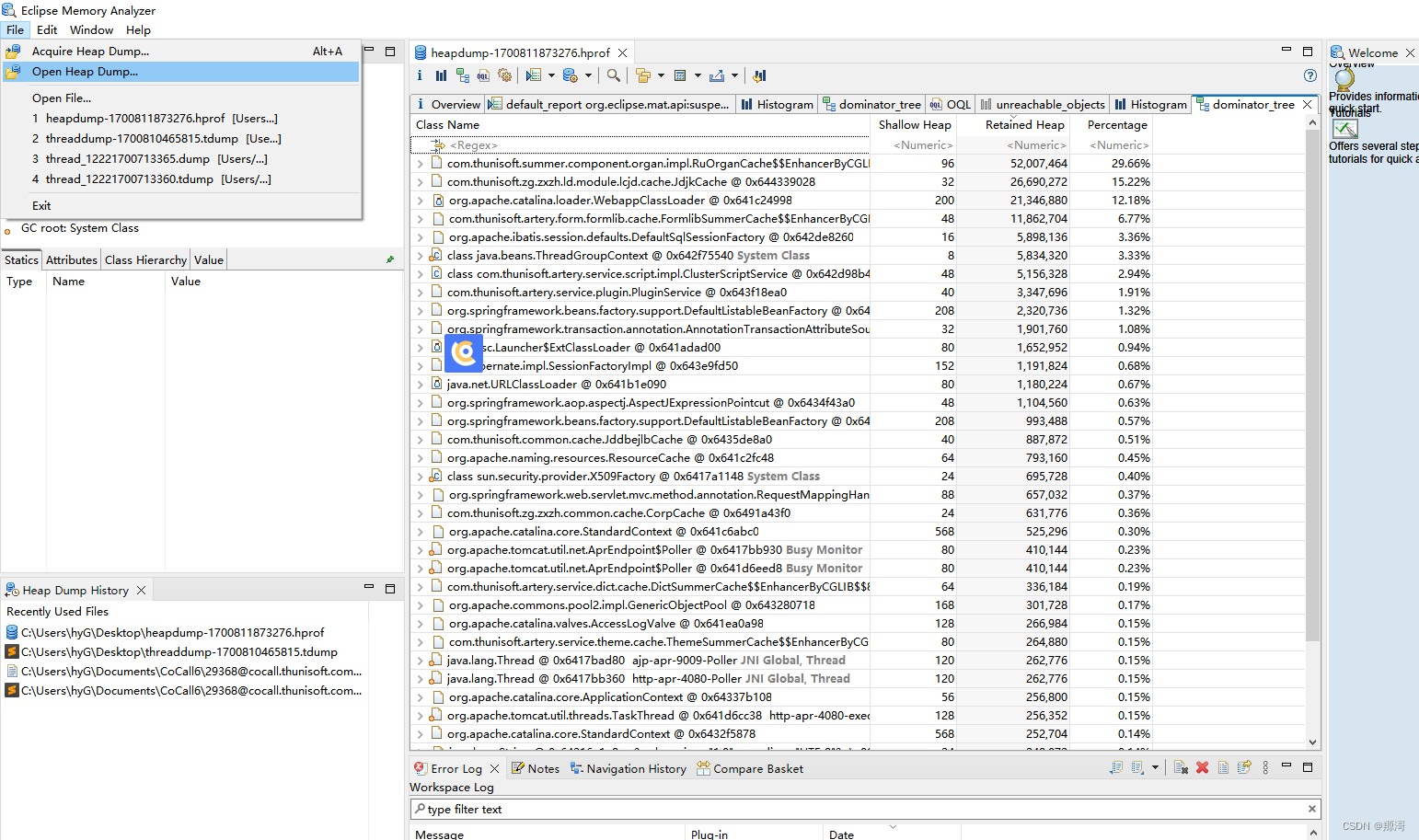
JVM 内存分析工具 MAT及实践
线程分析工具 MAT 官网下载地址:http://www.eclipse.org/mat/downloads.php mat百度网盘链接:(速度更快) 链接:https://pan.baidu.com/s/1tMp8MQIXuPtg9zBgruO0Ug?pwdjqtv 提取码:jqtv jdk17 百度网盘链接…...

jupyter notebook 不知道密码,怎么登录解决办法
jupyter notebook 不知道密码,怎么登录解决办法 1、 windows下,打开命令行,输入jupyter notebook list : C:\Users\tom>jupyter notebook list Currently running servers: http://localhost:8888/?tokenee8bb2c28a89c8a24d…...

软著项目推荐 深度学习中文汉字识别
文章目录 0 前言1 数据集合2 网络构建3 模型训练4 模型性能评估5 文字预测6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习中文汉字识别 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...
)
WEB渗透—反序列化(七)
Web渗透—反序列化 课程学习分享(课程非本人制作,仅提供学习分享) 靶场下载地址:GitHub - mcc0624/php_ser_Class: php反序列化靶场课程,基于课程制作的靶场 课程地址:PHP反序列化漏洞学习_哔哩哔_…...

牛客网刷题笔记四 链表节点k个一组翻转
NC50 链表中的节点每k个一组翻转 题目: 思路: 这种题目比较习惯现在草稿本涂涂画画链表处理过程。整体思路是赋值新的链表,用游离指针遍历原始链表进行翻转操作,当游离个数等于k时,就将翻转后的链表接到新的链表后&am…...
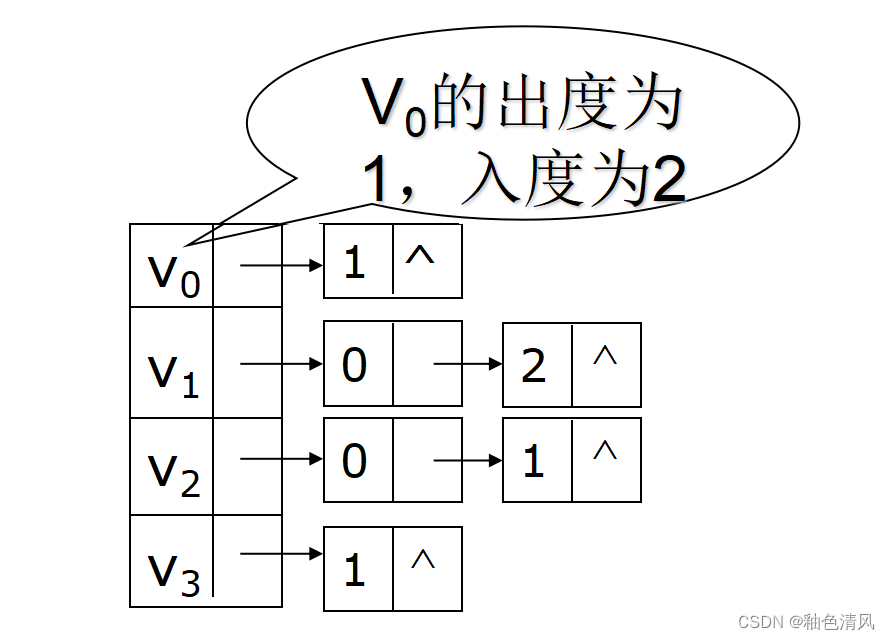
【数据结构】图<简单认识图>
对于下面的内容,大家着重观察和理解图即可,可以直接绕过一些文字性的概念,对图有一个大概的认识。 图 简单认识图图的定义有向图和无向图完全图无向完全图有向完全图 图的基本存储结构邻接矩阵存储邻接矩阵的优点 网络的邻接矩阵邻接表无向图…...

Git介绍和基础命令解析
Git基本操作指令 工作区和暂存区 Git管理的文件分为:工作区(本地的文件夹),版本库(.git文件夹),版本库又分为暂存区stage和暂存区分支master(仓库) 工作区>>>>暂存区>>>>仓库 git add把文件从工作区>>>…...
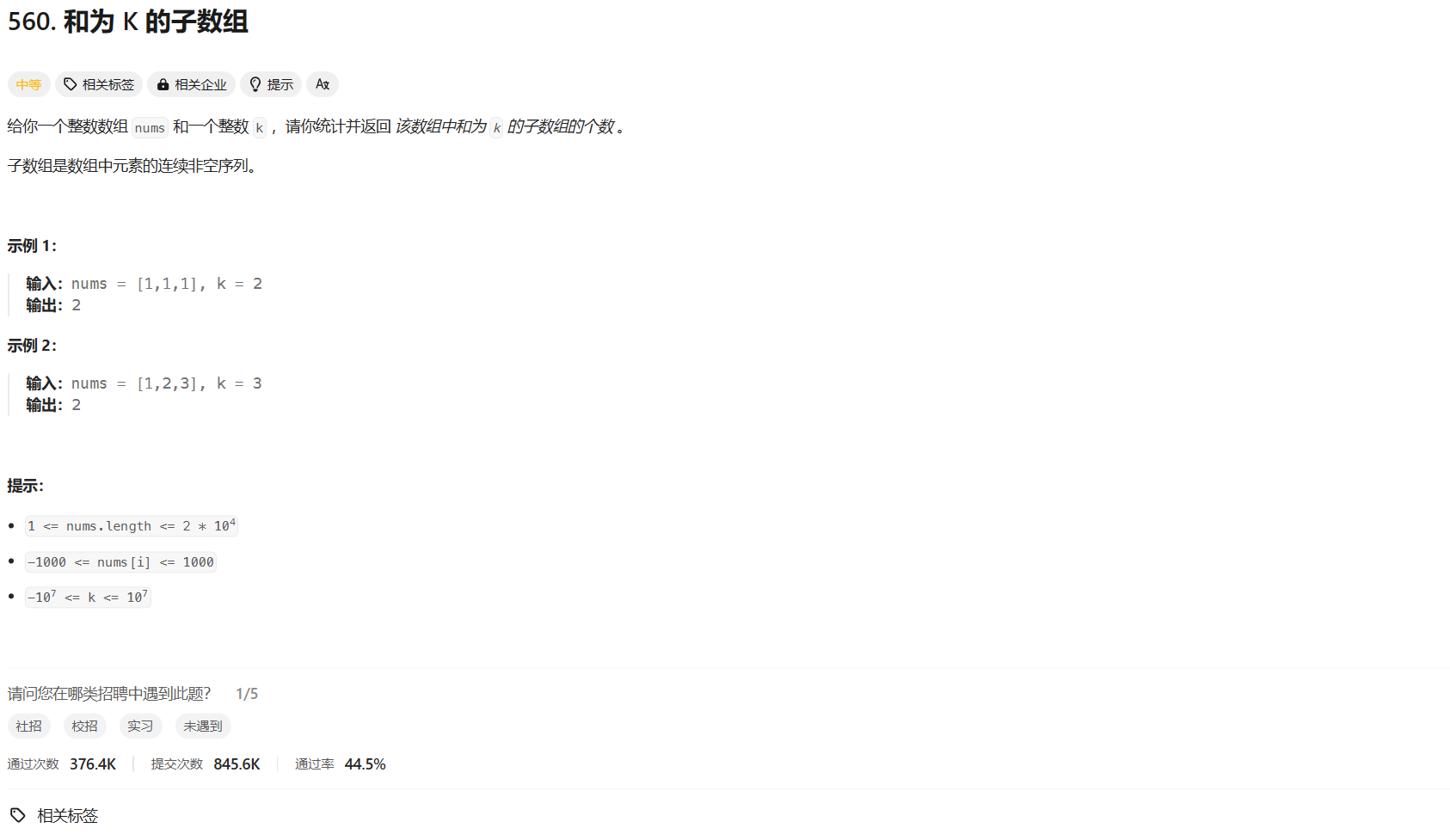
力扣hot100 和为 K 的子数组 前缀和
👨🏫 题目地址 🍻 AC code class Solution {public int subarraySum(int[] nums, int k){int ans 0;int n nums.length;int[] s new int[n 1];// 前缀和s[0] 0;s[1] nums[0];for (int i 2; i < n; i)s[i] s[i - 1] nums[i - 1…...
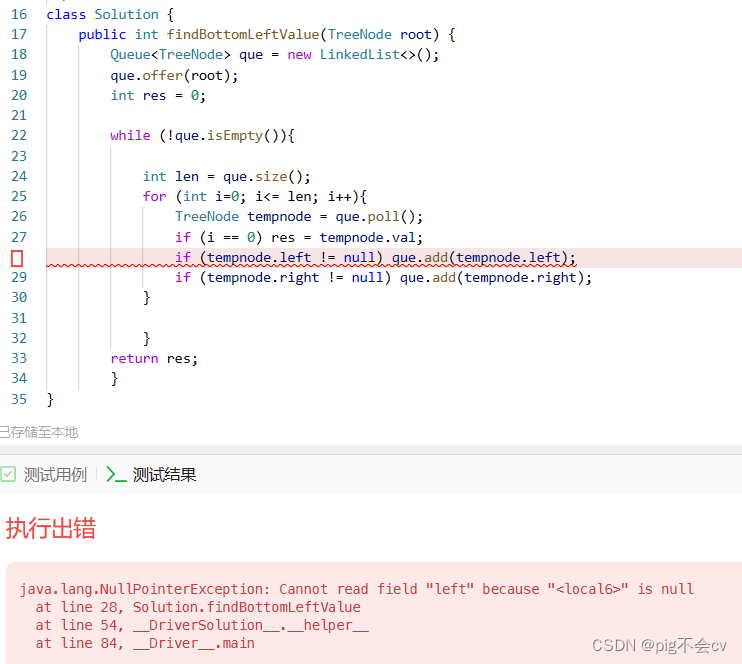
6.12找树左下角的值(LC513-M)
算法: 这道题适合用迭代法,层序遍历:按层遍历,每次把每层最左边的值保存、更新到result里面。 看看Java怎么实现层序遍历的(用队列): /*** Definition for a binary tree node.* public clas…...
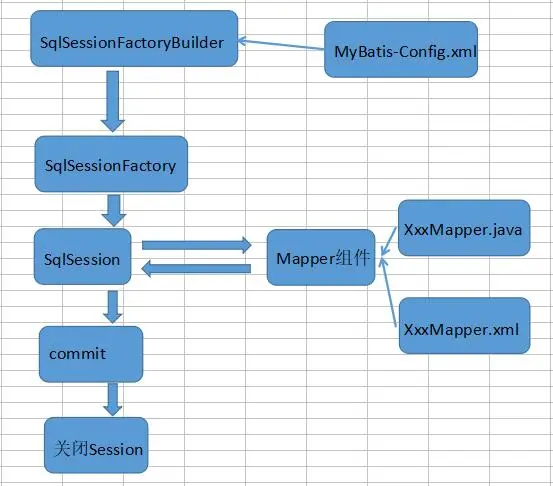
【精选】框架初探篇之——MyBatis的CRUD及配置文件
MyBatis增删改查 MyBatis新增 新增用户 持久层接口添加方法 void add(User user);映射文件添加标签 <insert id"add" parameterType"com.mybatis.pojo.User">insert into user(username,sex,address) values(# {username},# {sex},# {address}) <…...

ES8语法async与await
async和await两种语法结合可以让异步代码像同步代码一样。 一、async函数 async函数的返回值为Promise对象promise对象的结果由async函数执行的返回值决定 async function fn() {// 返回一个字符串return 字符串;// 返回的结果不是一个Promise类型的对象…...

c#处理SQLSERVER 中image数量类型为空
项目场景: DataRow dataRow dataTable.Rows[i]; var pxpicture dataRow ["pxImage"];if (pxpicture!null){byte[] pic (byte[])pxpicture;acs.Add("pxpicture", Convert.ToBase64String(pic));}问题描述 代码执行出现错误: 无…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...