24. 深度学习进阶 - 矩阵运算的维度和激活函数

Hi,你好。我是茶桁。
咱们经过前一轮的学习,已经完成了一个小型的神经网络框架。但是这也只是个开始而已,在之后的课程中,针对深度学习我们需要进阶学习。
我们要学到超参数,优化器,卷积神经网络等等。看起来,任务还是蛮重的。
行吧,让我们开始。
矩阵运算的维度
首先,我们之前写了一份拓朴排序的代码。那我们是否了解在神经网络中拓朴排序的作用。我们前面讲过的内容大家可以回忆一下,拓朴排序在咱们的神经网络中的作用不是为了计算方便,是为了能计算。
换句话说,没有拓朴排序的话,根本就没法计算了。Tensorflow和PyTourh最大的区别就是,Tensorflow在运行之前必须得把拓朴排序建好,PyTorch是在运行的过程中自己根据我们的连接状况一边运行一边建立。但是它们都有拓朴排序。
拓朴排序后要进行计算,那就要提到维度问题,在进行机器学习的时候一定要确保我们矩阵运算的维度正确。我们来看一下示例就明白我要说的了。
x = torch.from_numpy(np.random.random(size=(4, 10)))
print(x.shape)---
torch.Size([4, 10])
假如说,现在我们生成了一个4,10的矩阵,也就是4行10列。
from torch import nn
linear = nn.Linear(in_features=10, out_features=5).double()
print(linear(x).shape)---
torch.Size([4, 5])
然后我们来给他定义一个线性变化,in_features=10,这个就是必须的, 然后,out_features=5,假如把它分成5类。
这个时候,你看他就变成一个四行五列的一个东西了。
刚才我们说了,in_features=10是必须的,如果这个值我们设置成其他的,比如说8,那就不行了,运行不了。会收到警告:mat1 and mat2 shapes cannot be multiplied (4x10 and 8x5)
我们再给它来一个Softmax
nonlinear = nn.Softmax()
print(nonlinear(linear(x)))
这样,我们就得到了一个4*5的概率分布。
我们把这个非线性函数换一下,换成Sigmoid, 之前的Softmax赋值给yhat, 咱们做一个多层的:
yhat = nn.Softmax()
nonlinear = nn.Sigmoid()
linear2 = nn.linear(in_features=n, out_features=8).double()print(yhat(linear2(nonlinear(linear(x)))))
好,这个时候,我还并没有给in_features赋值,我们来想想,这个时候应该赋值是多少?也就是说,我们现在的linear2到底传入的特征是多少?
我们这里定义的linear和linear2其实就是w*x+b。
那这里我们来推一下,第一次使用linear的时候,我们得到了4*5的矩阵对吧?nonlinear并没有改变矩阵的维度。现在linear2中,那我们in_features赋值就得是5对吧?
yhat = nn.Softmax()
nonlinear = nn.Sigmoid()
linear2 = nn.linear(in_features=5, out_features=8).double()print(yhat(linear2(nonlinear(linear(x)))).shape)---
torch.Size([4, 8])
然后我们就得到了一个4*8的维度的矩阵。
那其实在PyTorch里提供了一种比较简单的方法,就叫做Sequential:
model = nn.Sequential(nn.Linear(in_features=10, out_features=5).double(),nn.Sigmoid(),nn.Linear(in_features=5, out_features=8).double(),nn.Softmax(),
)print(model(x).shape)---
torch.Size([4, 8])
这样,我们就把刚才几个函数方法按顺序都一个一个的写在Sequential里,那其实刚才的过程,也就是解释了这个方法的原理。
接着,我们来写一个ytrue:
ytrue = torch.randint(8, (4, ))
loss_fn = nn.CrossEntropyLoss()print(model(x).shape)
print(ytrue.shape)---
torch.Size([4, 8])
torch.Size([4])
现在ytrue就是CrossEntropyLoss输入的一个label值。
然后我们就可以进行反向传播了:
loss.backward()for p in model.parameters():print(p, p.grad)---
Parameter containing:
tensor([...])
...
求解反向传播之后就可以得到它的梯度了。然后再经过一轮一轮的训练,就可以把梯度稳定在某个值,这就是神经网络进行学习的一个过程。那主要是在这个过程中,一定要注意矩阵前后的大小。
激活函数
然后我们来看看激活函数的重要性。
在我们之前的课程中,我们提到过一个概念「激活函数」,不知道大家还有没有印象。那么激活函数的作用是什么呢? 是实现非线性拟合对吧?
打比方来说,如果我们现在要拟合一个函数f(x) = w*x+b, 你把它再给送到一个g(x), 再比如g(x)=w2*x+b,我们来做一个拟合,那么g(f(x)), 那是不是还是一样,g(f(x)) = w2*(w*x+b)+b, 然后就变成w2*w*x + w2*b + b, 那其实这个就还是一个线性函数。
我们每一段都给它进行一个线性变化,再进行一个非线性变化,再进行一个线性变化,一段一段这样折起来,理论上它可以拟合任何函数。
这个怎么理解?其实我们如何用已知的函数去拟合函数在高等数学里边是一个一直在学习,一直在研究的东西。学高数的同学应该知道,高数里面有一个著名的东西叫做傅立叶变化,这是一种线性积分变换,用于函数在时域和频域之间的变换。
我们给定任意一个复杂的函数,都可以通过sin和cos来把它拟合出来,其关键思想是任何连续、周期或非周期的函数都可以表示为正弦和余弦函数的组合。通过计算不同频率的正弦和余弦成分的系数an和bn, 我们可以了解一个函数的频谱特性,即它包含那些频率成分。
f ( x ) = a 0 + ∑ n = 1 0 ( a n c o s ( 2 π n f x ) + b n s i n ( 2 π n f x ) ) \begin{align*} f(x) = a_0 + \sum_{n=1}^0(a_n cos(2\pi nfx) + b_n sin(2\pi n fx)) \end{align*} f(x)=a0+n=1∑0(ancos(2πnfx)+bnsin(2πnfx))
除此之外,我们还有一个泰勒展开。我在数学篇的时候有仔细讲解过这个部分,大家可以回头去读一下我那篇文章,应该是数学篇第13节课,在那里我曾说过,所有的复杂函数都是用泰勒展开转换成多项式函数计算的。
之前有同学给我私信,也有同学在我文章下留言,说到某个位置看不懂了,还是数学拖了后腿。但是其实只是应用的话无所谓,但是如果想在这个方面有所建树,想要做些不一样的东西出来,还是要把数学的东西好好补一下的。
OK,那其实呢,我们的深度学习本质上其实就是在做这么一件事情,就是来自动拟合,到底是由什么构成的。
大家再来想一下,一个比较重要的,就是反向传播和前向传播。这个我们前面的课程里有详细的讲过,就是,我们的前向传播和反向传播的作用是什么。
那现在我们学完前几节了,回过头来我们想想,前向传播的作用是什么?反向传播的这个作用呢?
现在,假如说我已经训练出来了一个模型,我要用这个模型去预测。那么第一个问题是,预测的时候需不需要求loss?第二个是我需不需要做反向传播?
然后我们再来思考一个问题,如果我们需要求loss对于某个参数wi的偏导 ∂ l o s s ∂ w i \frac{\partial loss}{\partial w_i} ∂wi∂loss,那么我们首先需要进行反向传播对吧?那我们在进行反向传播之前,能不能不进行前向传播?
也就是说,我们把这个模型放在这里,一个x,然后输入进去得到一个loss。那么咱们训练了一轮之后,我们能不能在求解的时候不进行前向传播,直接进行反向传播?
我们只要知道,求loss值需要预测值就明白了。
那我们继续来思考,loss值和precision、recall等等的关系是什么?这些是什么?我们之前学习过,这些是评测指标对吧?也就是再问,loss和评测指标的关系是什么?
也就是说,我们能不能用precision,能不能用precision来做我们的loss函数?不能对吧,无法求导。
所以在整个机器学习的过程中,如果要有反向传播、梯度下降,必须得是可导的。像我们所说的MSE是可导的,cross-entropy也是可以求导的。
那如果上过我之前课程的同学应该记得,可求导的的函数需要满足什么条件?光滑性和连续性对吧?连续性呢,是可求导的一个必要条件,但不是充分条件,还必须在某个点附近足够光滑,以使得导数存在。
对于loss函数的设定,第一点,一定是要能求偏导的。第二呢,就是它一定得是一个凸函数:Convex functions。
那什么叫做凸函数呢?如果一个函数上的任意两点连线上的函数值都不低于这两点的函数值的线段,就称为凸函数。常见的比如线性函数,指数函数,幂函数,绝对值函数等都是凸函数。
想象一下,有一辆车,从a点开到b点,如果这个车在a点到b点的时候方向盘始终是打在一个方向的,那我们就说它是凸函数。
不过在一些情况下有些函数它不是凸函数,就在数学上专门有一个研究领域,Convex optimization,凸优化其实就是解决对于这种函数怎么样快速的求出他的基值,另外一个就是对于这种非凸函数怎么把它变成凸函数。
不同的激活函数它有什么区别呢?在最早的时候,大家用的是Sigmoid:
σ ( z ) = 1 1 + e − z \begin{align*} \sigma(z)=\frac{1}{1+e^{-z}} \end{align*} σ(z)=1+e−z1
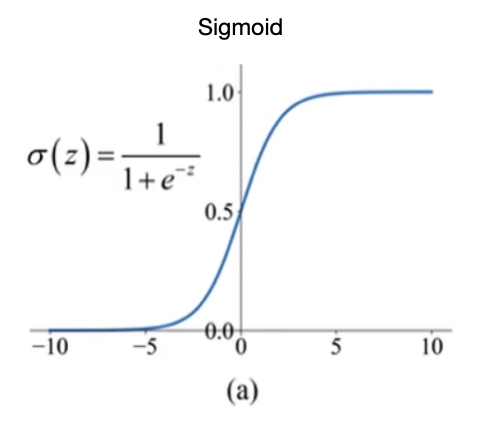
为什么最早用Sigmoid,这是因为Sigmoid有个天然的优势,就是它输出是0-1,而且它处处可导。
但是后来Sigmoid的结果有个e^x,指数运算就比较费时,这是第一个问题。第二个问题是Sigmoid的输出虽然是在0~1之间,但是平均值是0.5,对于程序来说,我们希望获得均值等于0,STD等于1。我们往往希望把它变成这样的一种函数,这样的话做梯度下降的时候比较好做。
于是就又提出来了一个更简单的方法,就是反正切函数:Tanh。
σ ( z ) = e z − e − z e z + e − z \sigma(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} σ(z)=ez+e−zez−e−z
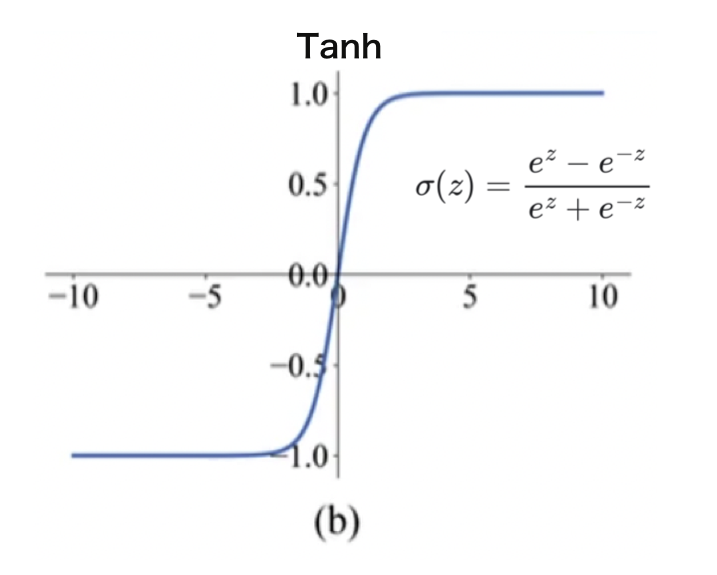
它的形式和Sigmoid很像,不同的是平均值,它的平均值是0。现在这个用的也挺多。
但是Tanh和sigmoid一样都有一个小问题,就是它的绝大多数地方loss都等于0, 那么wi大部分时候就没有办法学习,也就不会更新。
为了解决这个问题,就是有人提出来了一种非常简单的方法,就是ReLU:
R e L U ( z ) = { z , z > 0 0 , o t h e r w i s e \begin{align*} ReLU(z) = \begin{cases} z, z>0 \\ 0, otherwise \end{cases} \end{align*} ReLU(z)={z,z>00,otherwise
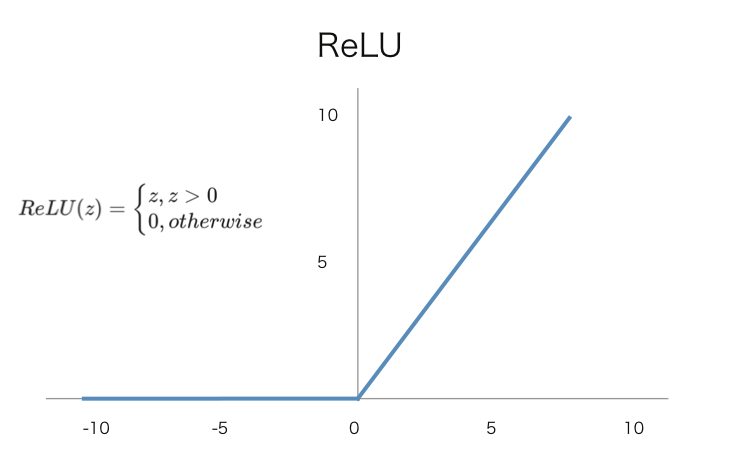
这种方法看似非常简单,但其实非常好用。它就是当一个x值经过ReLU的时候,如果它大于0就还保持原来的值,如果不大于0就直接把它变成0。
这样大家可能会觉得x<0时有这么多值没有办法求导,但其实比起sigmoid来说可求导的范围其实已经变多了。而且你会发现要对他x大于0的地方求偏导非常的简单,就直接等于1。
可以保证它肯定是可以做更新的,而且ReLU这种函数它是大量的被应用在卷积神经网络里边。
在咱们后面的课程中,会讲到卷积,它是有一个卷积核,[F1,F2,F3,F4]然后把它经过ReLU之后,可能会变成[F1,0,F3,0]。那我们只要更新F1,F3就可以了,下一次再经过某种方式,在重新把F2和F4我们重新计算一下。
也就是说现在的wx+b不像以前一样,只有一个w,如果x值等于0,那整个都等于0. 而是我们会有一个矩阵,它部分等于0也没关系。而且它的求导会变得非常的快,比求指数的导数快多了。
那其实这里还有一个小问题,面试的时候可能会问到,就是ReLU其实在0点的时候不可导,怎么办?
这个很简单,可以在函数里边直接设置一下,直接给他一个0的值就可以了,就是在代码里面加一句话。
再后来,又有人提出了一种方法:LeakyRelU:
L e a k y R e L U ( z ) = { z , z > 0 a z , o t h e r w i s e LeakyReLU(z) = \begin{cases} z, z>0 \\ az, otherwise \end{cases} LeakyReLU(z)={z,z>0az,otherwise
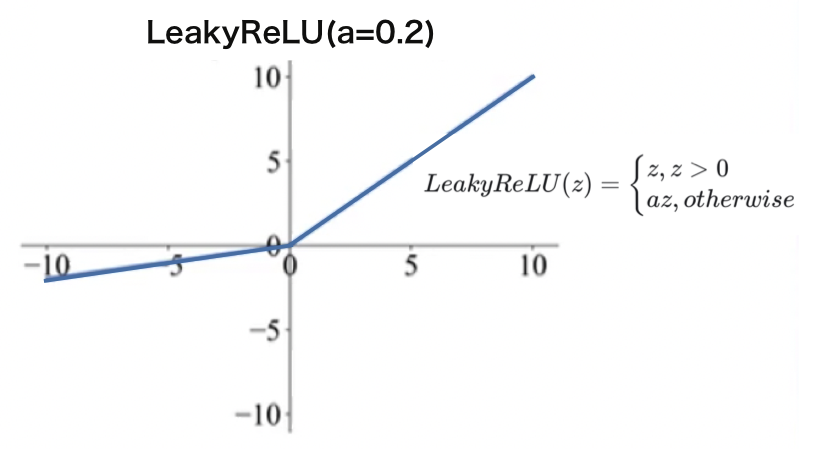
它把小于0的这些地方,也加了一个很小的梯度,这样的话大于0的时候partial就恒等于1,小于的时候partial也恒等于一个值,比如定一个a=0.2, 都可以。那这样就可以实现处处有导数。
但是其实用的也不太多,因为我们事实上发现在这种卷积神经网络里边,我们每一次把部分的权重设置成0不更新,反而可以提升它的训练效率,我们反而可以每次把训练focus on在几个参数上。
好,下节课,咱们来看看初始化的内容。
相关文章:

24. 深度学习进阶 - 矩阵运算的维度和激活函数
Hi,你好。我是茶桁。 咱们经过前一轮的学习,已经完成了一个小型的神经网络框架。但是这也只是个开始而已,在之后的课程中,针对深度学习我们需要进阶学习。 我们要学到超参数,优化器,卷积神经网络等等。看…...
杰发科技AC7801——keil工程移植到IAR
0、简介 发现AC7801的代码只有keil工程的,IAR和Eclipse的代码只有一个例程,于是在从Keil移植到IAR时候遇到的问题记录下。 正常情况下,直接把keil的usr用户代码移植到iar的文件夹下面,删除原本的文件再添加新加进来的文件即可。…...
Word怎么看字数?简单教程分享!
“我在写文章时,总是想看看写了多少字。但是我发现我的Word无法看到字数。在Word中应该怎么查看字数呢?请帮帮我!” Word是一个广泛使用的文档编辑工具。在我们编辑文章时,如果想查看写了多少字,也是可以轻松完成的。 …...
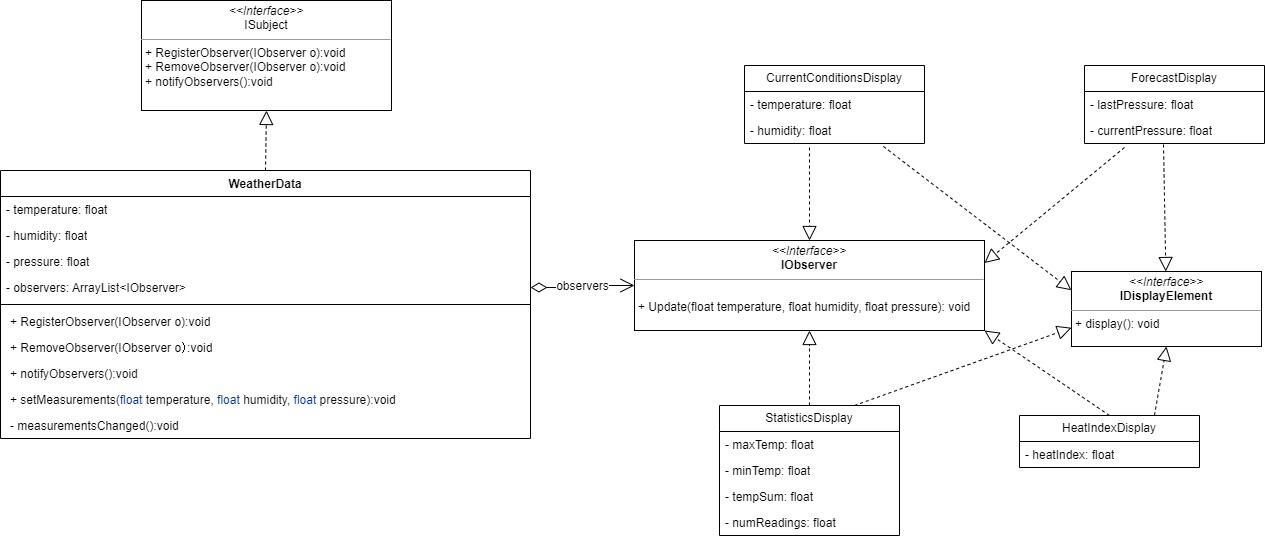
万字解析设计模式之观察者模式、中介者模式、访问者模式
一、观察者模式 1.1概述 观察者模式是一种行为型设计模式,它允许一个对象(称为主题或可观察者)在其状态发生改变时,通知它的所有依赖对象(称为观察者)并自动更新它们。这种模式提供了一种松耦合的方式&…...
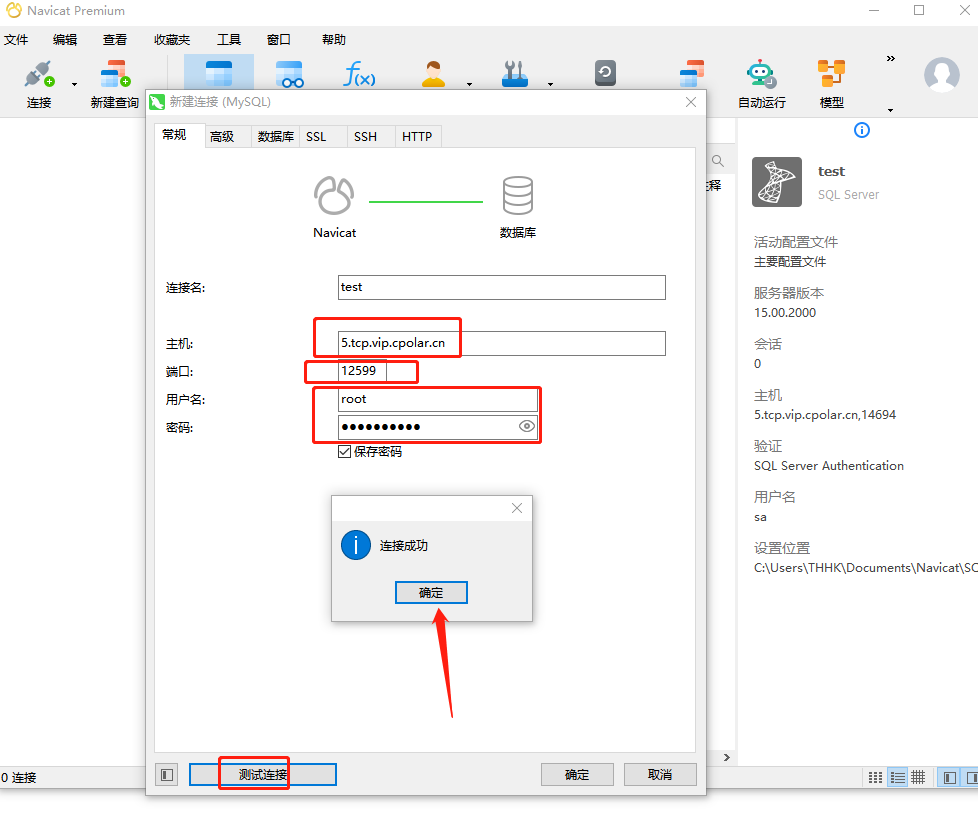
【MySQL | TCP】宝塔面板结合内网穿透实现公网远程访问
文章目录 前言1.Mysql服务安装2.创建数据库3.安装cpolar3.2 创建HTTP隧道4.远程连接5.固定TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 宝塔面板的简易操作性,使得运维难度降低,简化了Linux命令行进行繁琐的配置&#x…...

Python break用法详解
Python 语言没有提供 goto 语句来控制程序的跳转,这种做法虽然提高了程序流程控制的可读性,但降低了灵活性。为了弥补这种不足,Python 提供了 continue 和 break 来控制循环结构。本节先讲解 break 的用法。 某些时候,需要在某种…...
【C++初阶】STL详解(五)List的介绍与使用
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...

MySQL特点和基本语句
MySQL MySQL是一种流行的关系型数据库管理系统,由瑞典MySQL AB公司开发,现属于甲骨文公司(Oracle)旗下产品。MySQL是基于C语言开发的,它具有高性能、可扩展性、易用性等特点,并且支持大量的用户访问。 My…...

Gin 学习笔记03-参数绑定
参数绑定 1、ShouldBindJSON2、ShouldBindQuery3、ShouldBindUri4、ShouldBind 1、ShouldBindJSON package mainimport ("github.com/gin-gonic/gin""net/http" )type User struct {Name string json:"name"Gender string json:"gender&…...

【100天精通Python】Day73:python机器学习入门算法详解与代码示例
目录 1. 监督学习算法: 1.1 线性回归(Linear Regression): 1.2 逻辑回归(Logistic Regression): 1.3 决策树(Decision Tree): 1.4 支持向量机ÿ…...
Node.js入门指南(四)
目录 express框架 express介绍 express使用 express路由 express 响应设置 中间件 路由模块化 EJS 模板引擎 express-generator hello,大家好!上一篇文章我们介绍了Node.js的模块化以及包管理工具等知识,这篇文章主要给大家分享Nod…...
Java LeetCode篇-深入了解关于数组的经典解法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 轮转数组 1.1 使用移位的方式 1.2 使用三次数组逆转法 2.0 消失的数字 2.1 使用相减法 2.2 使用异或的方式 3.0 合并两个有序数组 3.1 使用三指针方式 3.2 使用合…...
- 无重复字符的最长子串)
LeeCode前端算法基础100题(4)- 无重复字符的最长子串
一、问题详情: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s "bbbbb…...

Axios简单使用与配置安装-Vue
安装Axios npm i axios main.js 导入 import Axios from axios Vue.prototype.$axios Axios简单发送请求 get getTest() {this.$axios({method: GET,url: https://apis.jxcxin.cn/api/title?urlhttps://apis.jxcxin.cn/}).then(res > {//请求成功回调console.log(res)}…...
【初始前后端交互+原生Ajax+Fetch+axios+同源策略+解决跨域】
初始前后端交互原生AjaxFetchaxios同源策略解决跨域 1 初识前后端交互2 原生Ajax2.1 Ajax基础2.2 Ajax案例2.3 ajax请求方式 3 Fetch3.1 fetch基础3.2 fetch案例 4 axios4.1 axios基础4.2 axios使用4.2.1 axios拦截器4.2.2 axios中断器 5 同源策略6 解决跨域6.1 jsonp6.2 其他技…...
C语言--每日选择题--Day24
第一题 1. 在C语言中,非法的八进制是( ) A:018 B:016 C:017 D:0257 答案及解析 A 八进制是0~7的数字,所以A错误 第二题 2. fun((exp1,exp2),(exp3,exp4,exp5))有几…...
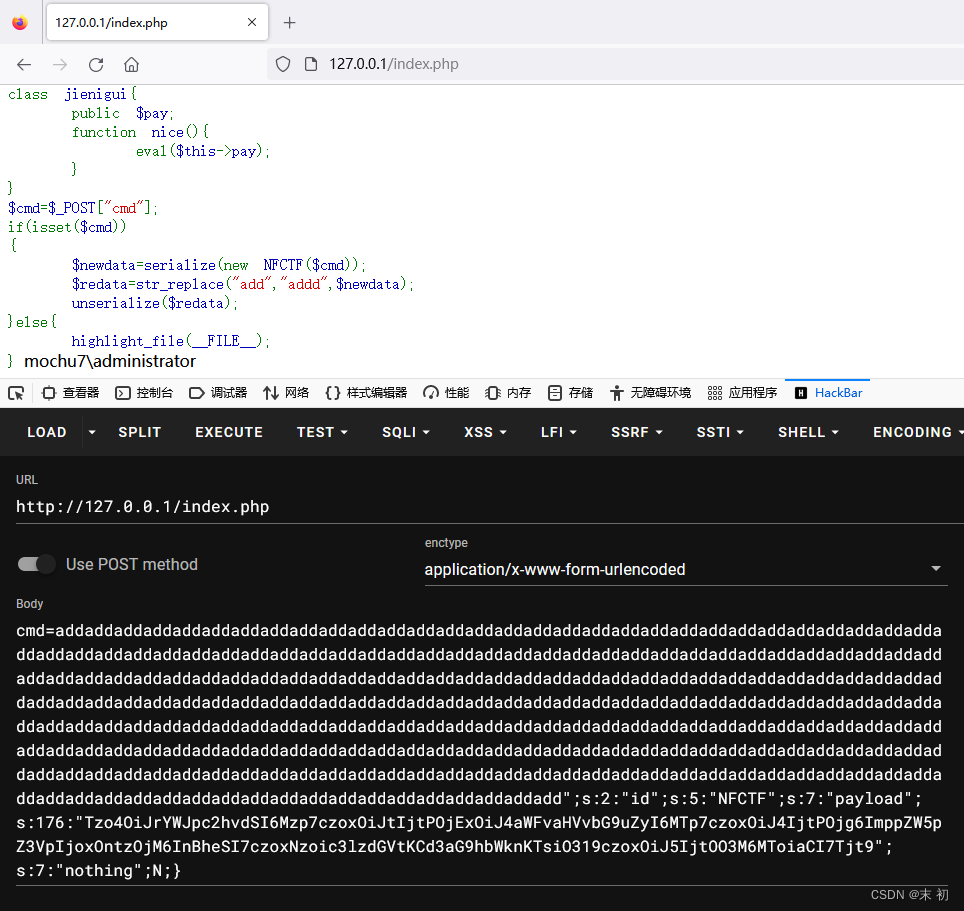
记一次简单的PHP反序列化字符串溢出
今天朋友给的一道题,让我看看,来源不知,随手记一下 <?php // where is flag error_reporting(0); class NFCTF{ public $ming,$id,$payload,$nothing;function __construct($iii){$this->ming$ii…...

找工作面试技巧
问题描述:找工作时,不知道如何回答问题怎么办。 问题解决:可以尝试使用STAT原则来回答问题。具体如下。 "STAR" 原则是一种常用于回答面试问题的方法,特别是在描述个人经验、解决问题或展示技能和能力时。"STAR&q…...
Jackson无缝替换Fastjson
目录 文章目录 一,Fastjson到Jackson的替换方案方案代码序列化反序列化通过key获取某种类型的值类型替换 二,Springboot工程中序列化的使用场景三,SpringMVC框架中的Http消息转换器1,原理:2,自定义消息转换…...
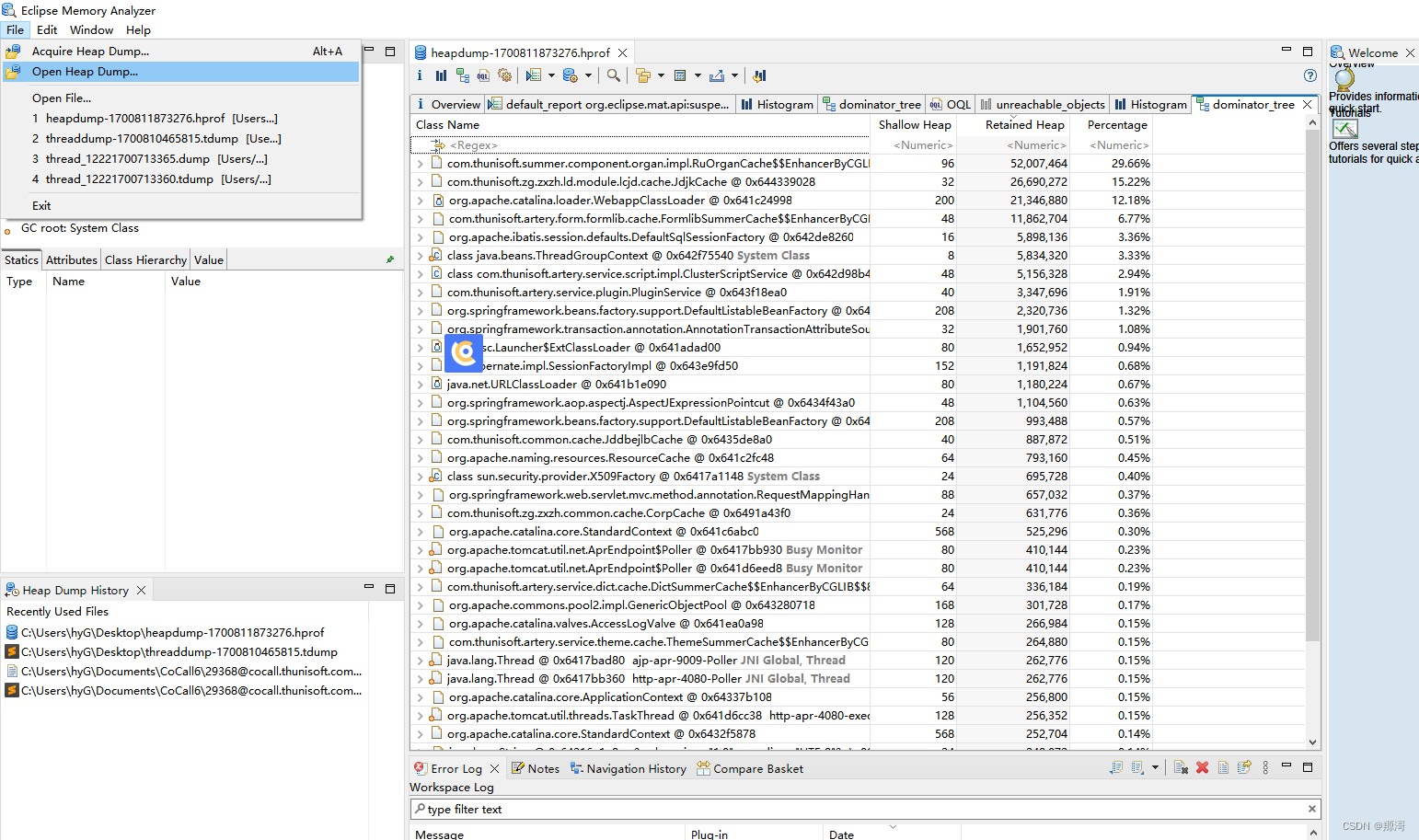
JVM 内存分析工具 MAT及实践
线程分析工具 MAT 官网下载地址:http://www.eclipse.org/mat/downloads.php mat百度网盘链接:(速度更快) 链接:https://pan.baidu.com/s/1tMp8MQIXuPtg9zBgruO0Ug?pwdjqtv 提取码:jqtv jdk17 百度网盘链接…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
