【100天精通Python】Day73:python机器学习入门算法详解与代码示例
目录
1. 监督学习算法:
1.1 线性回归(Linear Regression):
1.2 逻辑回归(Logistic Regression):
1.3 决策树(Decision Tree):
1.4 支持向量机(Support Vector Machine):
1.5 随机森林(Random Forest):
2. 无监督学习算法:
2.1 聚类算法(Clustering):
2.2 主成分分析(PCA):
2.3 K均值聚类(K-means Clustering):
3. 集成学习算法:
3.1 随机森林(Random Forest):
3.2 梯度提升树(Gradient Boosting):
3.3 AdaBoost(Adaptive Boosting):
1. 监督学习算法:
- 线性回归(Linear Regression):用于建模连续变量之间的线性关系。示例:预测房屋价格。
- 逻辑回归(Logistic Regression):用于建模二分类问题。示例:判断一封电子邮件是垃圾邮件还是正常邮件。
- 决策树(Decision Tree):通过构建树形结构进行分类或回归。示例:预测购买某个产品的用户。
- 支持向量机(Support Vector Machine):通过找到一个最优的超平面将数据分类。示例:预测肿瘤是否为恶性。
- 随机森林(Random Forest):基于多个决策树的集成算法,通过投票方式进行预测。示例:预测客户是否流失。
1.1 线性回归(Linear Regression):
-
详解:线性回归用于建立连续变量之间的线性关系模型。
-
示例代码:
from sklearn.linear_model import LinearRegression# 准备训练数据
X_train = [[1], [2], [3], [4], [5]] # 自变量的训练数据
y_train = [2, 4, 6, 8, 10] # 因变量的训练数据# 创建模型对象
model = LinearRegression()# 拟合模型
model.fit(X_train, y_train)# 预测
X_test = [[6], [7], [8]] # 自变量的测试数据
y_pred = model.predict(X_test) # 预测因变量# 输出预测结果
print("预测结果:", y_pred)1.2 逻辑回归(Logistic Regression):
- 详解:逻辑回归用于建立二分类问题的模型,输出是概率值。
- 示例代码
from sklearn.linear_model import LogisticRegression# 准备训练数据
X_train = [[1, 2], [2, 1], [2, 3], [4, 5]] # 自变量的训练数据
y_train = [0, 0, 1, 1] # 因变量的训练数据# 创建模型对象
model = LogisticRegression()# 拟合模型
model.fit(X_train, y_train)# 预测
X_test = [[3, 4], [1, 1], [5, 6]] # 自变量的测试数据
y_pred = model.predict(X_test) # 预测因变量# 输出预测结果
print("预测结果:", y_pred)1.3 决策树(Decision Tree):
- 详解:决策树通过构建树形结构进行分类或回归,选择最佳特征进行划分。
- 示例代码:
from sklearn.tree import DecisionTreeClassifier# 准备训练数据
X_train = [[1, 2], [2, 1], [2, 3], [4, 5]] # 自变量的训练数据
y_train = [0, 0, 1, 1] # 因变量的训练数据# 创建模型对象
model = DecisionTreeClassifier()# 拟合模型
model.fit(X_train, y_train)# 预测
X_test = [[3, 4], [1, 1], [5, 6]] # 自变量的测试数据
y_pred = model.predict(X_test) # 预测因变量# 输出预测结果
print("预测结果:", y_pred)1.4 支持向量机(Support Vector Machine):
- 详解:支持向量机通过找到一个最优的超平面将数据分类,可以处理线性和非线性问题。
- 示例代码:
from sklearn.svm import SVC# 准备训练数据
X_train = [[1, 2], [2, 1], [2, 3], [4, 5]] # 自变量的训练数据
y_train = [0, 0, 1, 1] # 因变量的训练数据# 创建模型对象
model = SVC()# 拟合模型
model.fit(X_train, y_train)# 预测
X_test = [[3, 4], [1, 1], [5, 6]] # 自变量的测试数据
y_pred = model.predict(X_test) # 预测因变量# 输出预测结果
print("预测结果:", y_pred)1.5 随机森林(Random Forest):
随机森林(Random Forest)是一种基于决策树的集成学习算法,它通过训练多个决策树并集成它们的预测结果来提高模型的准确性和泛化能力。
- 随机森林由多颗决策树组成,每颗树都是独立而相互不相关的。
- 每颗决策树在构建时,会从原始训练集中进行有放回地随机采样(bootstrap),形成一个新的训练集,并使用该训练集构建决策树。
- 在构建决策树的过程中,对于每个节点的特征选择,随机森林会从所有特征中随机选取一部分特征。
- 最后,随机森林通过集成所有决策树的预测结果,使用投票或平均的方式进行分类或回归。
示例代码:
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 加载数据集
data = load_iris()
X = data.data
y = data.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建随机森林模型
model = RandomForestClassifier(n_estimators=100, random_state=42)# 训练模型
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print("准确度:", accuracy)2. 无监督学习算法:
- 聚类算法(Clustering):将相似的数据点聚集到一起。示例:对市场细分进行分析。
- 主成分分析(PCA):通过线性变换将高维数据降维至低维空间。示例:图像识别中的特征提取。
- K均值聚类(K-means Clustering):将数据分成K个簇,使得每个数据点属于最近的簇。示例:对顾客进行细分。
2.1 聚类算法(Clustering):
- 详解:聚类算法是一种无监督学习方法,将相似的数据点聚集到一起,形成若干个簇。聚类算法可以帮助我们发现数据集中的内在结构和模式,用于市场细分、推荐系统、图像分割等领域。
- 示例代码:
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs# 创建示例数据
X, y = make_blobs(n_samples=100, centers=3, random_state=42)# 创建聚类模型
model = KMeans(n_clusters=3, random_state=42)# 进行聚类
y_pred = model.fit_predict(X)# 输出聚类结果
print("聚类结果:", y_pred)2.2 主成分分析(PCA):
- 详解:主成分分析是一种常用的降维方法,通过线性变换将高维数据转换为低维空间。它找到数据中最大方差的方向,即第一主成分,然后在与第一主成分正交的方向上找到第二主成分,依此类推。主成分分析可以用于减少特征维度、去除冗余信息以及可视化高维数据。
- 示例代码:
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris# 加载鸢尾花数据集
data = load_iris()
X = data.data# 创建PCA模型
model = PCA(n_components=2)# 进行主成分分析
X_pca = model.fit_transform(X)# 输出降维后的数据
print("降维后的数据:", X_pca)
2.3 K均值聚类(K-means Clustering):
- 详解:K均值聚类是一种迭代的聚类算法。它将数据集划分为K个簇,并使得每个数据点属于最近的簇的中心点。K均值聚类常用于数据分析、图像分割、文本挖掘等任务。
- 示例代码:
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs# 创建示例数据
X, y_true = make_blobs(n_samples=300, centers=4, random_state=42)# 创建K均值聚类模型
model = KMeans(n_clusters=4, random_state=42)# 进行聚类
model.fit(X)# 获取聚类标签
y_pred = model.labels_# 输出聚类结果
print("聚类结果:", y_pred)3. 集成学习算法:
随机森林(Random Forest):通过多个决策树的集成进行分类或回归。示例:预测房价
梯度提升树(Gradient Boosting):通过训练多个弱模型,并逐步拟合残差来优化整体模型。示例:预测销售额。
AdaBoost(Adaptive Boosting):通过逐步调整样本权重,训练多个弱分类器并加权投票。示例:人脸识别。
3.1 随机森林(Random Forest):
- 详解:随机森林通过多个决策树的集成进行分类或回归。每个决策树在构建时以随机的方式选择特征子集,并使用自助采样的方式构建每棵树的训练数据集。最后,随机森林通过投票(分类)或平均(回归)决策树的结果来得出最终预测。
- 示例代码:
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error# 加载数据集
data = fetch_california_housing()
X = data.data
y = data.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建随机森林模型
model = RandomForestRegressor(n_estimators=100, random_state=42)# 训练模型
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
mse = mean_squared_error(y_test, y_pred)
print("均方误差:", mse)3.2 梯度提升树(Gradient Boosting):
- 详解:梯度提升树通过训练多个弱模型,并逐步拟合当前模型的残差来优化整体模型。每一轮训练时,前一轮的残差成为当前轮的目标变量。最后,梯度提升树将多个弱模型加权求和得到最终预测结果。
- 示例代码:
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error# 加载数据集
data = fetch_california_housing()
X = data.data
y = data.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建梯度提升树模型
model = GradientBoostingRegressor(n_estimators=100, random_state=42)# 训练模型
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
mse = mean_squared_error(y_test, y_pred)
print("均方误差:", mse)3.3 AdaBoost(Adaptive Boosting):
- 详解:AdaBoost通过逐步调整样本权重,训练多个弱分类器并加权投票的方式进行分类。每个弱分类器权重取决于其在之前轮次中的分类误差。最后,AdaBoost将多个弱分类器组合成一个强分类器。
- 示例代码:
from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import fetch_olivetti_faces
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 加载数据集
data = fetch_olivetti_faces()
X = data.data
y = data.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建AdaBoost模型
model = AdaBoostClassifier(n_estimators=100, random_state=42)# 训练模型
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print("准确度:", accuracy)相关文章:

【100天精通Python】Day73:python机器学习入门算法详解与代码示例
目录 1. 监督学习算法: 1.1 线性回归(Linear Regression): 1.2 逻辑回归(Logistic Regression): 1.3 决策树(Decision Tree): 1.4 支持向量机ÿ…...
Node.js入门指南(四)
目录 express框架 express介绍 express使用 express路由 express 响应设置 中间件 路由模块化 EJS 模板引擎 express-generator hello,大家好!上一篇文章我们介绍了Node.js的模块化以及包管理工具等知识,这篇文章主要给大家分享Nod…...
Java LeetCode篇-深入了解关于数组的经典解法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 轮转数组 1.1 使用移位的方式 1.2 使用三次数组逆转法 2.0 消失的数字 2.1 使用相减法 2.2 使用异或的方式 3.0 合并两个有序数组 3.1 使用三指针方式 3.2 使用合…...
- 无重复字符的最长子串)
LeeCode前端算法基础100题(4)- 无重复字符的最长子串
一、问题详情: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s "bbbbb…...

Axios简单使用与配置安装-Vue
安装Axios npm i axios main.js 导入 import Axios from axios Vue.prototype.$axios Axios简单发送请求 get getTest() {this.$axios({method: GET,url: https://apis.jxcxin.cn/api/title?urlhttps://apis.jxcxin.cn/}).then(res > {//请求成功回调console.log(res)}…...
【初始前后端交互+原生Ajax+Fetch+axios+同源策略+解决跨域】
初始前后端交互原生AjaxFetchaxios同源策略解决跨域 1 初识前后端交互2 原生Ajax2.1 Ajax基础2.2 Ajax案例2.3 ajax请求方式 3 Fetch3.1 fetch基础3.2 fetch案例 4 axios4.1 axios基础4.2 axios使用4.2.1 axios拦截器4.2.2 axios中断器 5 同源策略6 解决跨域6.1 jsonp6.2 其他技…...
C语言--每日选择题--Day24
第一题 1. 在C语言中,非法的八进制是( ) A:018 B:016 C:017 D:0257 答案及解析 A 八进制是0~7的数字,所以A错误 第二题 2. fun((exp1,exp2),(exp3,exp4,exp5))有几…...
记一次简单的PHP反序列化字符串溢出
今天朋友给的一道题,让我看看,来源不知,随手记一下 <?php // where is flag error_reporting(0); class NFCTF{ public $ming,$id,$payload,$nothing;function __construct($iii){$this->ming$ii…...

找工作面试技巧
问题描述:找工作时,不知道如何回答问题怎么办。 问题解决:可以尝试使用STAT原则来回答问题。具体如下。 "STAR" 原则是一种常用于回答面试问题的方法,特别是在描述个人经验、解决问题或展示技能和能力时。"STAR&q…...
Jackson无缝替换Fastjson
目录 文章目录 一,Fastjson到Jackson的替换方案方案代码序列化反序列化通过key获取某种类型的值类型替换 二,Springboot工程中序列化的使用场景三,SpringMVC框架中的Http消息转换器1,原理:2,自定义消息转换…...
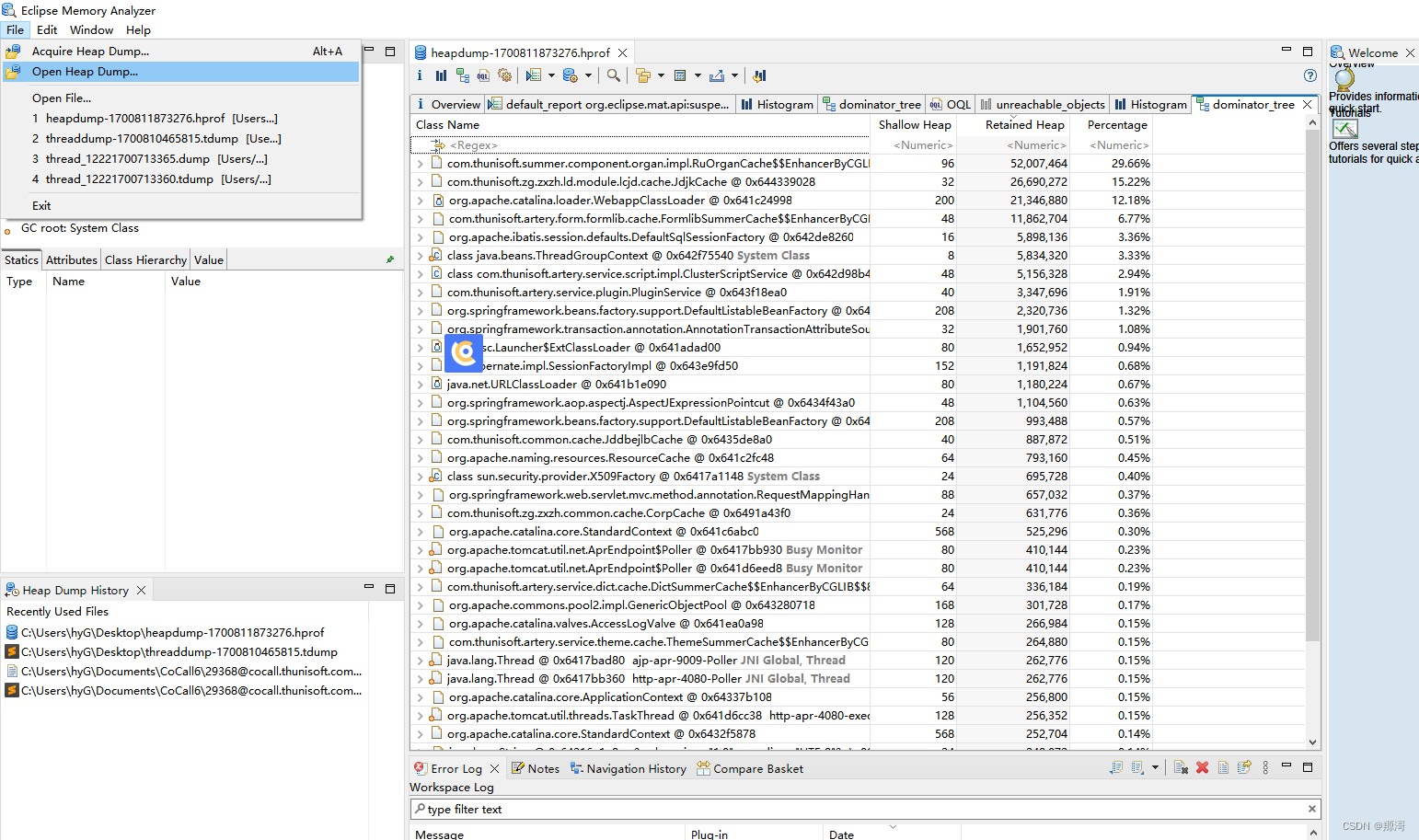
JVM 内存分析工具 MAT及实践
线程分析工具 MAT 官网下载地址:http://www.eclipse.org/mat/downloads.php mat百度网盘链接:(速度更快) 链接:https://pan.baidu.com/s/1tMp8MQIXuPtg9zBgruO0Ug?pwdjqtv 提取码:jqtv jdk17 百度网盘链接…...

jupyter notebook 不知道密码,怎么登录解决办法
jupyter notebook 不知道密码,怎么登录解决办法 1、 windows下,打开命令行,输入jupyter notebook list : C:\Users\tom>jupyter notebook list Currently running servers: http://localhost:8888/?tokenee8bb2c28a89c8a24d…...

软著项目推荐 深度学习中文汉字识别
文章目录 0 前言1 数据集合2 网络构建3 模型训练4 模型性能评估5 文字预测6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习中文汉字识别 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...
)
WEB渗透—反序列化(七)
Web渗透—反序列化 课程学习分享(课程非本人制作,仅提供学习分享) 靶场下载地址:GitHub - mcc0624/php_ser_Class: php反序列化靶场课程,基于课程制作的靶场 课程地址:PHP反序列化漏洞学习_哔哩哔_…...

牛客网刷题笔记四 链表节点k个一组翻转
NC50 链表中的节点每k个一组翻转 题目: 思路: 这种题目比较习惯现在草稿本涂涂画画链表处理过程。整体思路是赋值新的链表,用游离指针遍历原始链表进行翻转操作,当游离个数等于k时,就将翻转后的链表接到新的链表后&am…...
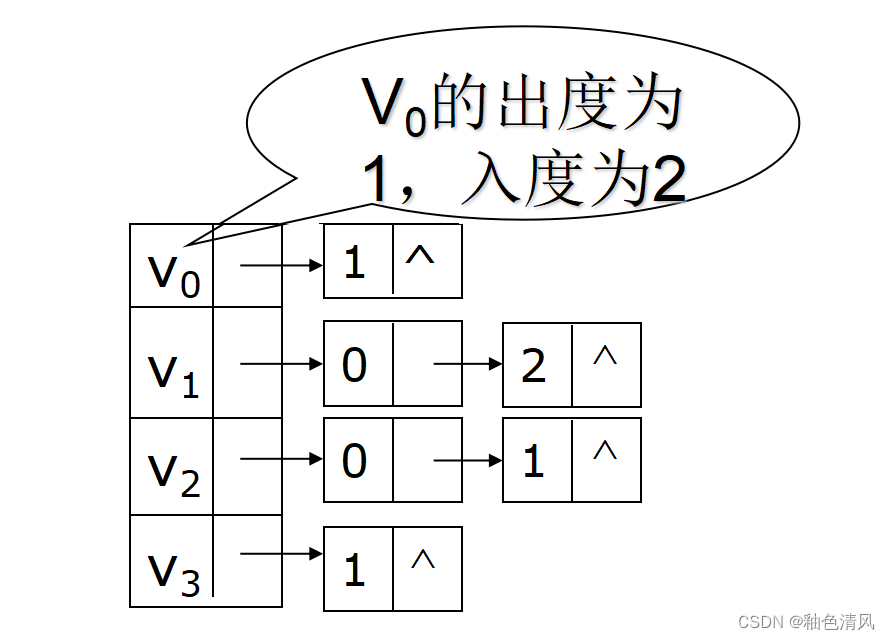
【数据结构】图<简单认识图>
对于下面的内容,大家着重观察和理解图即可,可以直接绕过一些文字性的概念,对图有一个大概的认识。 图 简单认识图图的定义有向图和无向图完全图无向完全图有向完全图 图的基本存储结构邻接矩阵存储邻接矩阵的优点 网络的邻接矩阵邻接表无向图…...

Git介绍和基础命令解析
Git基本操作指令 工作区和暂存区 Git管理的文件分为:工作区(本地的文件夹),版本库(.git文件夹),版本库又分为暂存区stage和暂存区分支master(仓库) 工作区>>>>暂存区>>>>仓库 git add把文件从工作区>>>…...
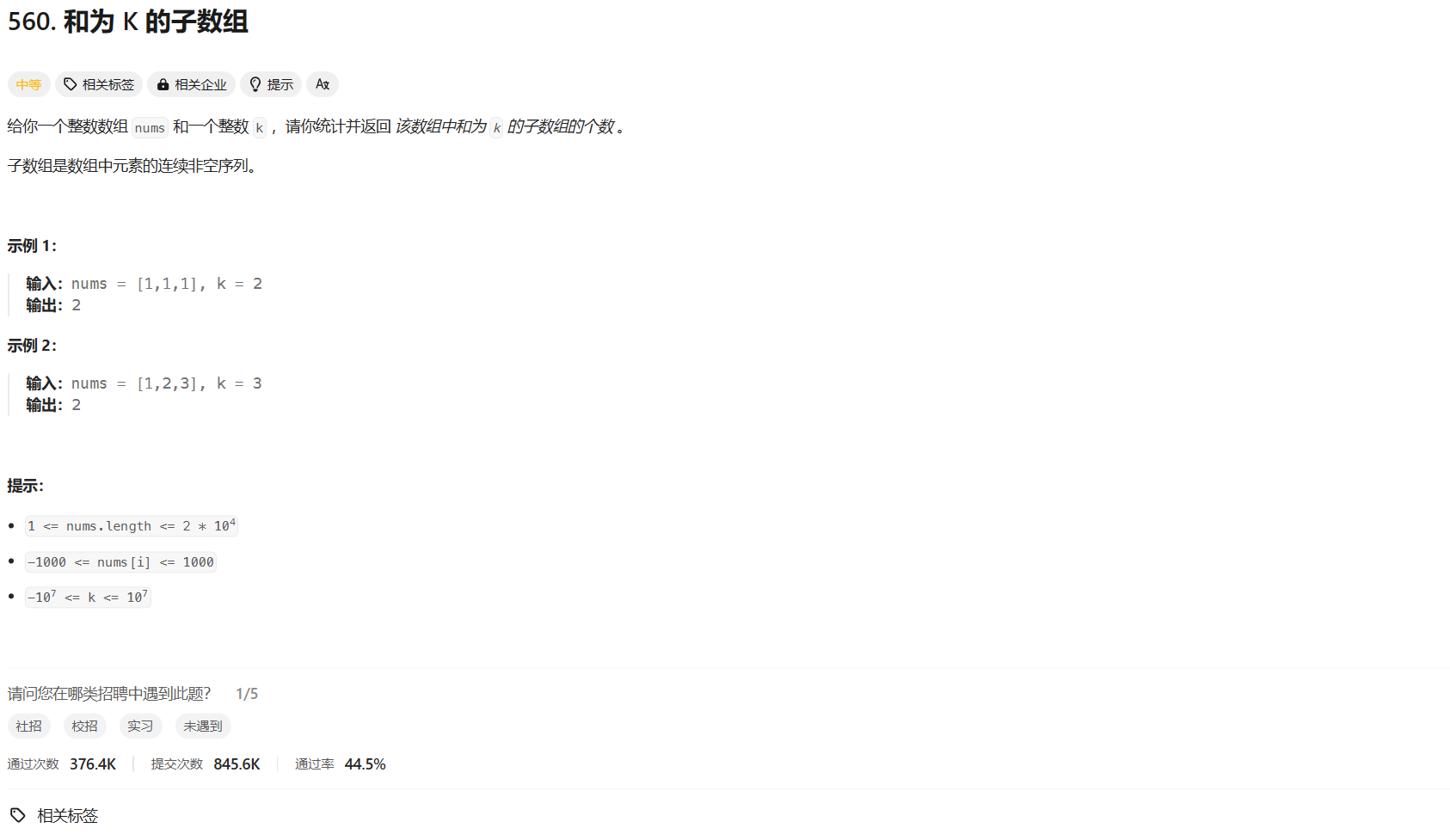
力扣hot100 和为 K 的子数组 前缀和
👨🏫 题目地址 🍻 AC code class Solution {public int subarraySum(int[] nums, int k){int ans 0;int n nums.length;int[] s new int[n 1];// 前缀和s[0] 0;s[1] nums[0];for (int i 2; i < n; i)s[i] s[i - 1] nums[i - 1…...
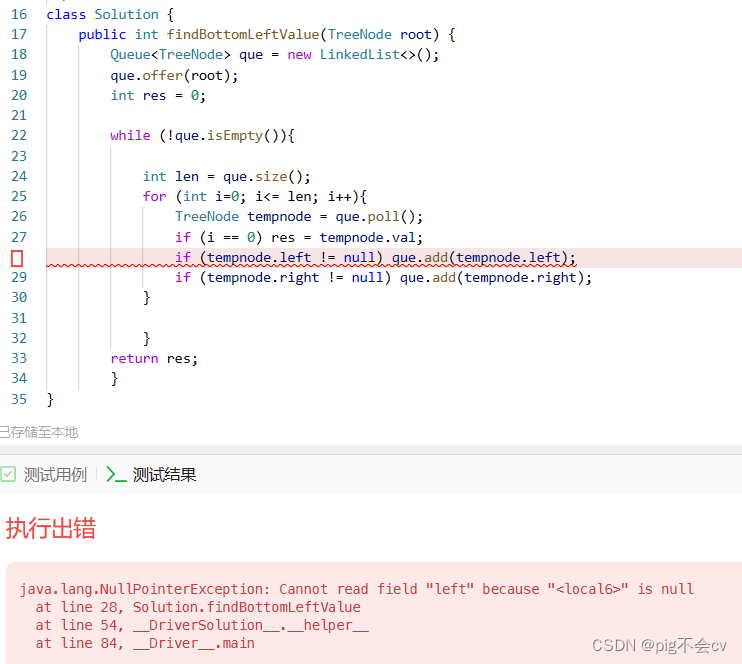
6.12找树左下角的值(LC513-M)
算法: 这道题适合用迭代法,层序遍历:按层遍历,每次把每层最左边的值保存、更新到result里面。 看看Java怎么实现层序遍历的(用队列): /*** Definition for a binary tree node.* public clas…...
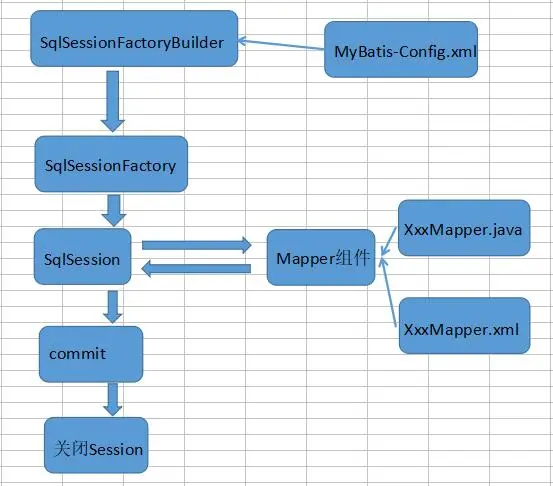
【精选】框架初探篇之——MyBatis的CRUD及配置文件
MyBatis增删改查 MyBatis新增 新增用户 持久层接口添加方法 void add(User user);映射文件添加标签 <insert id"add" parameterType"com.mybatis.pojo.User">insert into user(username,sex,address) values(# {username},# {sex},# {address}) <…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
