B树与B+树的对比
B树:
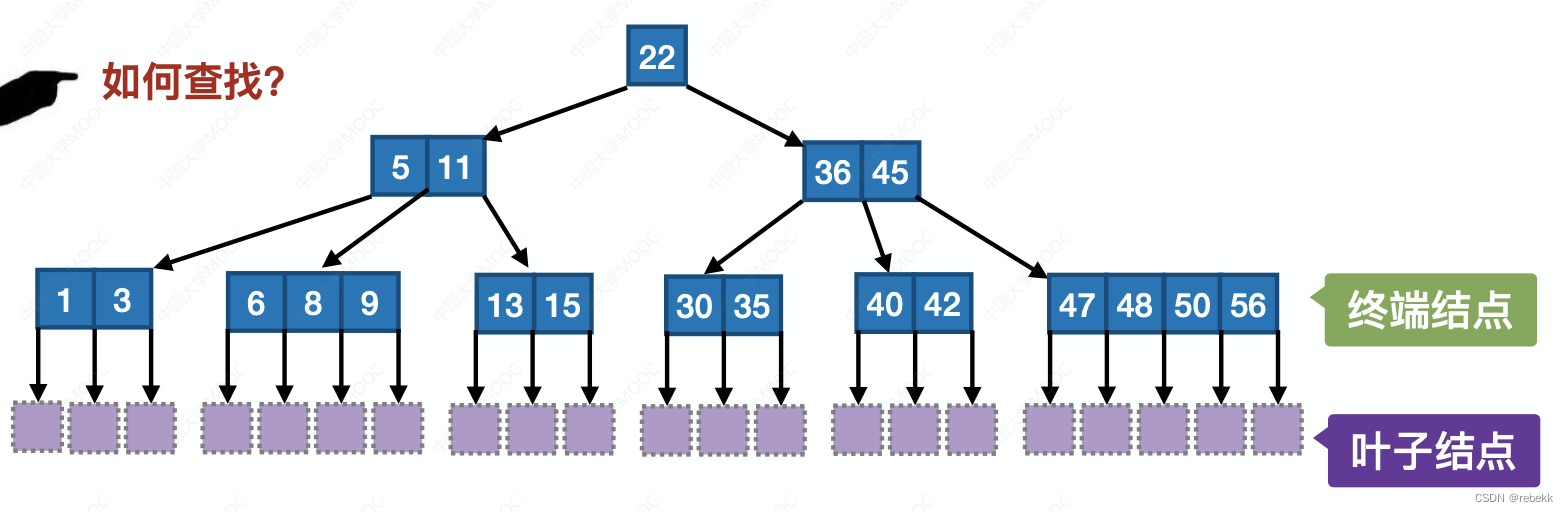
m阶B树的核心特性:
- 树中每个节点至多有m棵子树,即至多含有m-1个关键字
- 根节点的子树数属于[2, m],关键字数属于[1, m-1],其他节点的子树数属于 [ ⌈ m 2 ⌉ , m ] [\lceil \frac{m}{2}\rceil, m] [⌈2m⌉,m],关键字数属于 [ ⌈ m 2 ⌉ − 1 , m − 1 ] [\lceil \frac{m}{2}\rceil-1, m-1] [⌈2m⌉−1,m−1]
- 对任一节点,其所有子树高度都相同
- 关键字的值:子树0<关键字1<子树1<关键字2<…(类比二叉查找树 左<根<右)
- 所有叶节点都出现在同一层次上,且不带信息(可以视为外部节点或类似于折半查找判定树的查找失败节点,实际上这些节点不存在,指向这些节点的指针为空)
B+树
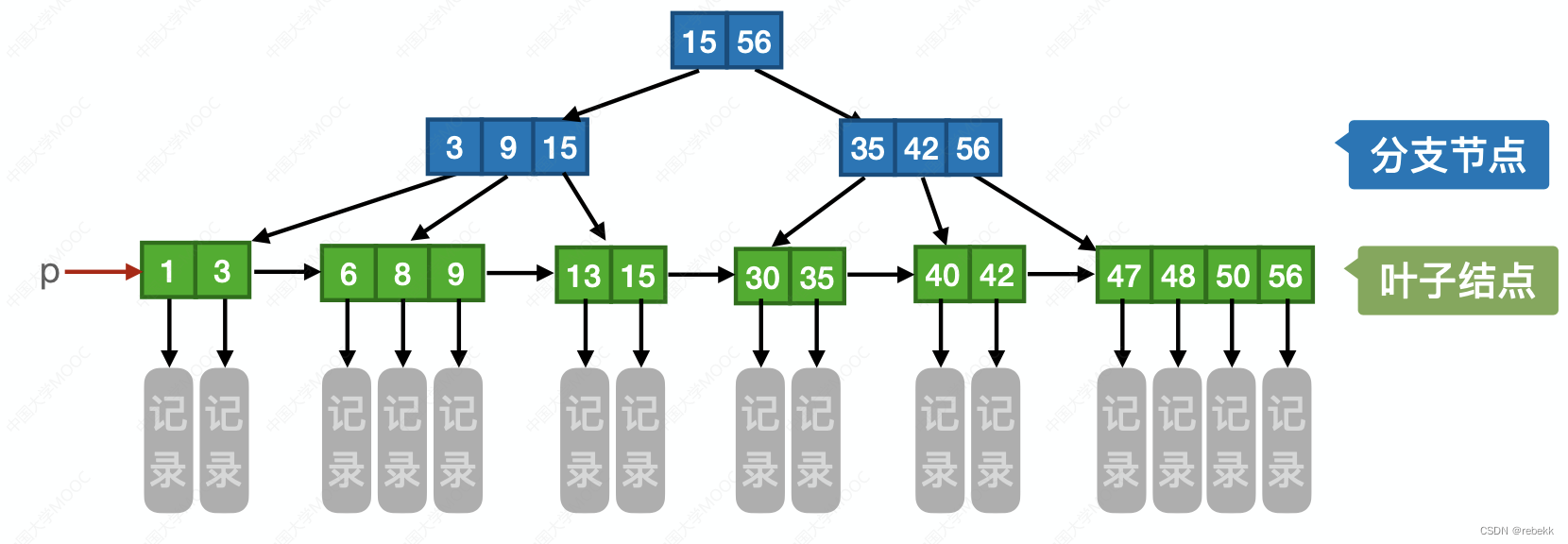
m阶B+树的核心特性:
- 通常在B+树上有两个头指针,一个指向根节点,另一个指向关键字最小的叶子节点。因此可对B+树进行两种查找运算,一种是从最小关键字起顺序查找,另一种是从根节点开始,进行随机查找
- 树中每个节点至多有m棵子树;(节点的子树个数与关键字个数相等)
- 根节点的子树数属于[2, m],其他节点的子树数属于 [ ⌈ m 2 ⌉ , m ] [\lceil \frac{m}{2}\rceil, m] [⌈2m⌉,m];(节点的子树个数与关键字个数相等)
- 所有叶节点包含全部关键字及指向相应记录的指针,叶节点中将关键字按大小顺序排列,并且相邻叶节点按大小顺序相互链接起来(支持顺序查找)
- 所有分支节点中仅包含它的各个子节点中关键字的最大值及指向其子节点的指针
- B+树中,无论查找成功与否,最终一定都要走到最下面一层节点(对比B树的查找,查找成功情况下,可能停在任何一层)
- B+树中,非叶节点不含有该关键字对应记录的存储地址,因此可以使一个磁盘块包含更多个关键字,使得B+树的阶更大,树高更矮,读磁盘次数更少,查找更快。典型应用如关系型数据库的“索引”(如MySQL)
二者对比
| - | B树 | B+树 |
|---|---|---|
| 关键字数与子树数 | 节点中的n个关键字对应n+1棵子树 | 节点中的n个关键字对应n棵子树 |
| 节点的关键字数范围 | 根节点的关键字数:[1, m-1],其他节点的关键字数[ ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉-1, m-1] | 根节点的关键字数:[1, m],其他节点的关键字数[ ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉, m] |
| 节点重复性 | 各节点中包含的关键字是不重复的 | 叶节点包含全部关键字,非叶节点中出现过的关键字也会出现在叶节点中 |
| 节点的作用 | B树的节点中都包含了关键字对应的记录的存储地址 | 叶节点包含信息,所有非叶节点仅起索引作用,非叶节点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针 |
| 来源 | m阶B树是二叉查找树的进化 | m阶B+树是分块查找的进化(进化为多级分块查找) |
| 查找方式 | 不支持顺序查找,查找成功时,可能停在任何一层节点,查找速度不稳定 | 支持顺序查找,查找成功或失败都会到达最下一层节点,查找速度稳定 |
相同点:
- 除根节点外,都最少 ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉个分叉(确保节点不要太空)
- 任何一个节点的子树都一样高(确保“绝对平衡”)
- 二者都是用于文件系统:
- B树主要用作文件的索引,因此它的查找涉及外存的存取。具体来讲,在B树上进行查找包含两种基本操作:
- 1)在B树中找节点:由于B树通常存储在磁盘上,因此查找操作1)是在磁盘上进行的
- 2)在节点中找关键字:这一查找操作是在内存中进行的,即在磁盘上找到指针p所指节点后,先将节点中的信息读入内存,然后再利用顺序查找或折半查找查询等于K的关键字
- 显然在磁盘上进行一次查找比在内存中进行一次查找耗费时间更多,因此在磁盘上进行查找的次数(即待查关键字所在节点在B树上的层次数)是决定B树查找效率的首要因素
- B+树是应文件系统所需而出的一种B树的变型树
- B树主要用作文件的索引,因此它的查找涉及外存的存取。具体来讲,在B树上进行查找包含两种基本操作:
相关文章:

B树与B+树的对比
B树: m阶B树的核心特性: 树中每个节点至多有m棵子树,即至多含有m-1个关键字根节点的子树数属于[2, m],关键字数属于[1, m-1],其他节点的子树数属于 [ ⌈ m 2 ⌉ , m ] [\lceil \frac{m}{2}\rceil, m] [⌈2m⌉,m]&am…...

关键路径-STL版/拓扑排序 关键路径【数据结构】
关键路径-STL版 题目描述 给定有向图无环的边信息,求每个顶点的最早开始时间、最迟开始时间。 输入 第一行图的顶点总数 第二行边的总数 第三行开始,每条边的时间长度,格式为源结点 目的结点 长度 输出 第一行:第个顶点的最早…...
最新AI创作系统ChatGPT系统运营源码,支持GPT-4图片对话能力,上传图片并识图理解对话,支持DALL-E3文生图
一、AI创作系统 SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧!本系统使用NestjsVueTypescript框架技术,持续集成AI能力到本系统。支持OpenAI DALL-E3文生图,…...

小航助学题库蓝桥杯题库stem选拔赛(21年3月)(含题库教师学生账号)
需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSDN博客 需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSD…...
[python]离线加载fetch_20newsgroups数据集
首先手动下载这个数据包 http://qwone.com/~jason/20Newsgroups/20news-bydate.tar.gz 下载这个文件后和脚本放一起就行,然后 打开twenty_newsgroups.py文件(在fetch_20newsgroups函数名上,右键转到定义即可找到) 之后运行代码即…...

Python与设计模式--代理模式
5-Python与设计模式–代理模式 一、网络服务器配置白名单 代理模式是一种使用频率非常高的模式,在多个著名的开源软件和当前多个著名的互联网产品后 台程序中都有所应用。下面我们用一个抽象化的简单例子,来说明代理模式。首先,构造一个网…...

ubuntu挂载磁盘,以及开机自动挂载磁盘
1. 挂载临时磁盘(关机自动取消挂载) 在Ubuntu上挂载磁盘涉及到几个步骤,其中包括查看可用磁盘、创建挂载点、编辑 /etc/fstab 文件以确保在系统启动时自动挂载等。以下是一般的步骤: **查看可用磁盘和分区:**可以使用…...
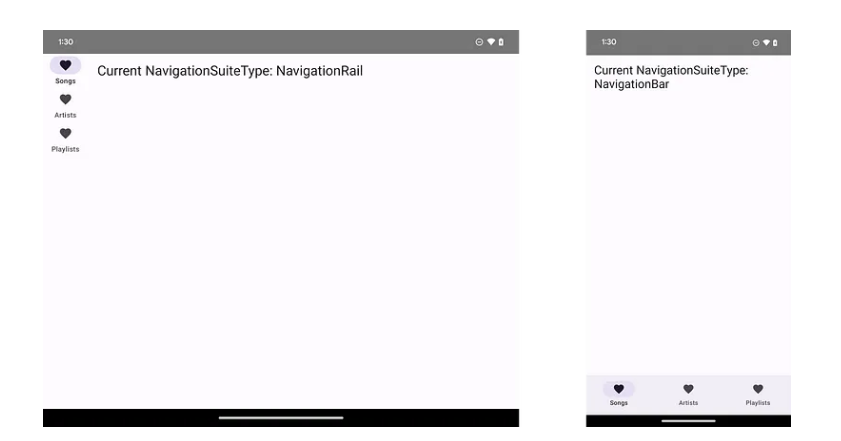
Jetpack Compose中适应性布局的新API
Jetpack Compose中适应性布局的新API 针对大屏幕优化的新组合件。 使用新的Material适应性布局,为手机、可折叠设备和平板电脑构建应用程序变得更加简单!市场上各种不同尺寸的Android设备的存在挑战了构建应用程序时对屏幕尺寸的通常假设。开发者不应该…...

小航助学题库蓝桥杯题库stem选拔赛(22年1月)(含题库教师学生账号)
需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSDN博客 需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSD…...

蓝桥杯第100 题 九宫幻方 DFS 全排列 C++ 解题思维
题目 九宫幻方https://www.lanqiao.cn/problems/100/learning/?page1&first_category_id1&name%E4%B9%9D 思路和解题方法 一 (DFS) 首先,定义了一些全局变量和数组。vis数组用于标记已经出现过的数字,a数组用于存储数独的初始状态…...

NOI / 1.10编程基础之简单排序 提问05:分数线划定 c语言 结构体
描述 世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。面试分数线根据计划录取人数的150%划定,即如果计划录取m名志愿者,则面试…...

再探Docker:从Docker基础到跨服务器部署
摘要: 这篇文章将从介绍Docker基础开始,逐步讲解如何创建镜像、使用Docker Compose编排容器、在Docker中更新部署环境,将更新后的环境打包为镜像并导出为tar包,最后在其他服务器上应用这个镜像。 1. Docker是什么 Docker是一种容…...
C# 使用PanGu分词
写在前面 这是官方介绍:盘古分词是一个中英文分词组件。作者eaglet 曾经开发过KTDictSeg 中文分词组件,拥有大量用户。作者基于之前分词组件的开发经验,结合最新的开发技术重新编写了盘古分词组件。 盘古分词组件需要配合其字典文件使用&am…...
Termius 一款优秀的跨平台 SSH 客户端工具
🔥🔥🔥 作为程序员或者运维管理人员,我们经常需要使用终端工具来进行服务器管理及各种操作,比如部署项目、调试代码、查看/优化服务、管理服务器等。 而实现远程服务器连接需要借助 SSH 协议来进行,SSH&am…...
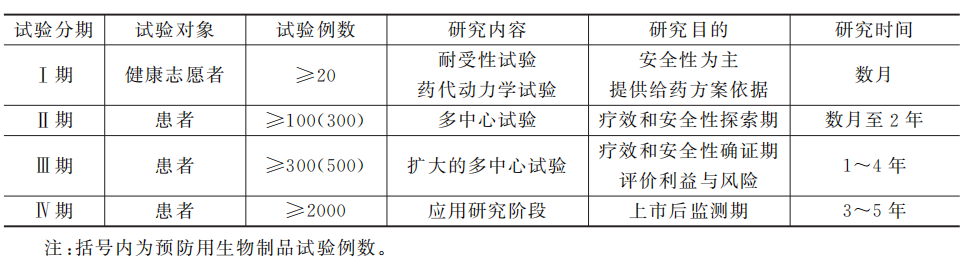
生命科学领域 - 新药从研发到上市全流程
新药是指新研制的、临床尚未应用的药物,其化学本质应为新的化合物或称新化学实体、 新 分子实体、新活性实体。新药研发的根本目的是治疗疑难危重疾病,研制出来的药物即使是全新的化学结构,但是疗效或安全性却不及现有的药物便失去新药价值&a…...
血的教训------入侵redis之利用python来破解redis密码
血的教训------入侵redis之利用python来破解redis密码 利用强大的python来进行redis的密码破解,过程不亦乐乎,当然也可以用shell脚本 本篇文章只供学习交流,请勿他用,谢谢。 其他相关联的文章 [1]VMware安装部署kail镜像服务器【…...

yolov8-pose 推理流程
目录 一、关键点预测 二、图像预处理 二、推理 三、后处理与可视化 3.1、后处理 3.2、特征点可视化 四、完整pytorch代码 yolov8-pose tensorrt 一、关键点预测 注:本篇只是阐述推理流程,tensorrt实现后续跟进。 yolov8-pose的tensorrt部署代码…...

笔记十七、认识React的路由插件react-router-dom和基本使用
react-router 分类 web使用 react-router-dom native使用 react-router-native anywhere(使用麻烦) react-router 安装 yarn add react-router-dom main.jsx import React from "react"; import ReactDOM from "react-dom/client"…...

CleanMyMac X4.14.5Crack最新Mac电脑清理优化最佳应用
CleanMyMac X 4.14.5是用于清理和优化Mac的最佳应用程序和强大工具。它看起来很棒而且很容易理解。该软件可以清理、保护、优化、稳定和维护您的 Mac 系统。您可以立即删除不必要的、不寻常的、无用的垃圾文件、损坏的文件垃圾,并释放大量内存空间。此外,…...

Linux shell单双引号区别
shell单双引号区别: Shell脚本中很多时候都在用单引号或双引号来框住字符串,但是他们之间是存在区别的 避免踩坑记录… 单引号 单引号中的任何字符都没有特殊含义,即一些转义字符,$ 变量引用都会无效,它只把他们当作一个单纯的…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
