数据结构——利用堆进行对数组的排序

今天文章的内容是关于我们如何利用堆的特性对我们的数组进行排序,还有就是我们的TopK的问题,这次我们放在的是文件种,我们放入一亿个数字,然后我们取出一亿个数字中最大的十个数,利用上章堆的问题进行解决。
首先就是我们如果对一个数组要进行排序,这个数组是没有任何规律的,就像下面的这个数组。
int arr[] = { 9,4,3,19,12,13,5,8,9 };
那我们得利用我们堆的特性,因为我们知道堆的特性,首先堆顶的数据一定是最小的,那我们要进行排序之前的话,要做的一个最重要的步骤就是先建立一个堆出来,我们可以用两种方法,一种是向上建堆,另一种就是向下建堆,这两个方法我们都会讲。
向上建堆
首先我们这里给的例子是升序,但是在升序的时候,我们是建立大堆还是小堆呢?答案是
大堆,那我们先来看看减小堆的时候,会产生怎样的问题,再来看看大堆,两者相互比较之后,我们就会发现升序就应该建立大堆。
首先就是复用我们上次堆的内容的向上建堆的那个方法,就是AdjustUp,如果这里大家不明白可以回头看看,我这里直接给出代码。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
我们可以看到这是向上调整,那我们建堆的过程是不是从二叉树的第二层开始往上建堆,比较的就是孩子和父亲的关系,那我们这里就可以写一个循环来完成这个建立堆的过程。
int arr[] = { 9,4,3,19,12,13,5,8,9 };for (int i = 1; i < sizeof(arr) / sizeof(arr[0]); i++){AdjustUp(arr, i);}
然后我们这个过程建立出来堆的样子就是我们的小堆
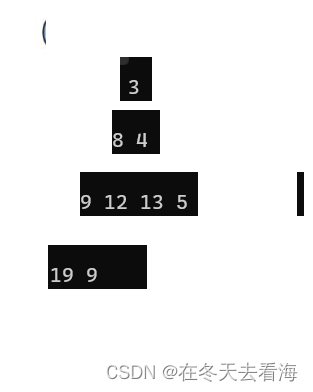
小堆建好之后,我们后面一步就是进行排序,但是排序有个问题,虽然我们保证了一开始堆顶的元素是最下的,但是我们怎么找出第二小,和第三小的数,如果我们这里有人说,我们可以利用堆的向下调整方法,然后重新建立堆,找出次小的,一次这样往下走就没问题,虽然说这样是可以完成排序,但是这样的排序方法甚至比冒泡还慢,看似用了堆的特性,其实时间复杂度比冒泡排序还高,那这样就没能完成我们堆的作用,但是如果我们建立大堆的话,结果·就·有所·不一样,我们可以不找小的,我们先排序后面的。
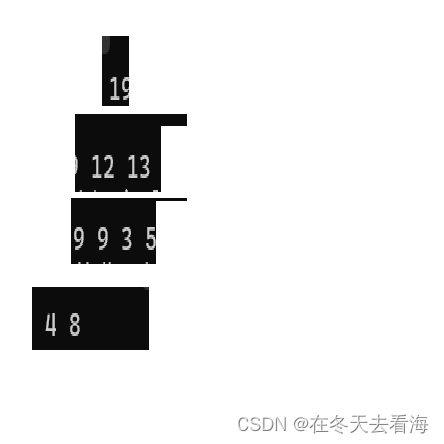
建立大堆后的样子,那我们可以先交换第一个元素和最后一个元素,然后再进行 向下调整,我们后面也会详细计算向下调整和向上调整的时间复杂度的,我们先来看如果交换第一个和最后一个元素的位置,那就变成下面这样。
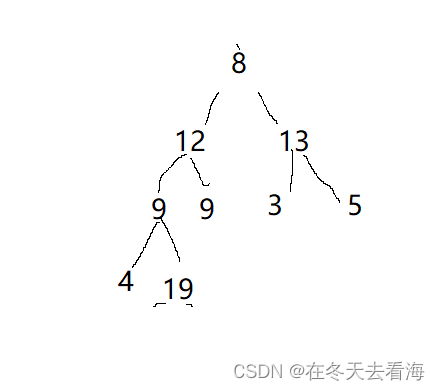
这是进行交换之后的样子,但是还是有问题,我们要保证我们这个还是大堆,那该怎么做呢,首先就是得向下调整,向下调整就是堆顶的元素往下调整,我们利用堆的特性之间写的AdjustDown,调整好之后,是下面的这个图。
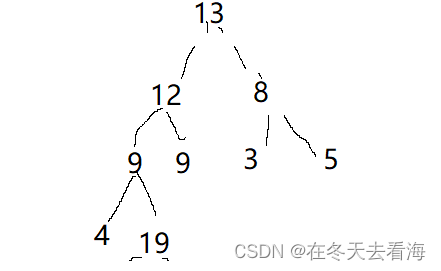
这个时候我们发现最后一个元素是最大的,有序的,而且我们还是大堆,那现在堆顶的元素就是次·大的数,所以现在要做的就是第一个和倒数第二个换位置,然后再进行调整,这样倒数两个的就是有序,有序之后他还是大堆,堆顶的元素就是第三个最大的数,这样一次循环,一直到最后就变成有序了。
那我们的代码就是下面这个,其实代码很简答的主要可能难理解。
AdjustDown
void AdjustDown(int* a, int size, int parent)
{int child = 2 * parent + 1;while (child < size){if (a[child + 1] > a[child] && child+1 < size){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
这个就是AdjustDown的代码,再堆里讲过,这样就不将了,来看我们如何进行排序的部分代码
int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//这里的end是元素个数,如果是下标的话就是指最后一个元素的后一个end--;}
end = 0的时候就说明已经排序好了,所以这个就是判断条件,然后来看我们的end一开始就是指向最后一个元素,因为是数组,所以这里表示的就是下标,我们这里就是要注意这个,然后先是交换堆顶元素和最后一个元素的问题,就直接开始调整,但是调整的时候我们end并没有进行–,因为
AdjustDown的size位置的参数表示的就是元素个素,然后我们调整的时候因为最后一个元素已经有序了,所以就不用在进行调整了。
我们来看看结果

可以发现我们也是排好序了,这里呢还有要讲一个内容就是建堆,我们那个时候建堆是向上调整,是从第二层开始的,我们也可以用向下建堆的方法,向下建堆要保证两边的子树都是堆,比如我们现在是大堆,所以子数就得是大堆,我们第一次进行调整得应该是第一个父亲节点,我们可以用(size - 1- 1)/ 2找到第一个父亲节点。因为我们堆虽然看起来是个二叉树,但是实际上就是一个数组,我们这里来看代码是如何实现得。
int main()
{int arr[] = { 9,4,3,19,12,13,5,8,9 };int n = sizeof(arr) / sizeof(arr[0]);for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}printf("\n");int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//这里的end是元素个数,如果是下标的话就是指最后一个元素的后一个end--;}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}return 0;
}
这个就是只用了向下调整进行排序,建堆得方法也是用的向下调整得这个方法,那我们后面得来计算一下向上调整和向下调整得时间复杂度,这里先给出得结论就是向下建堆的方法才是最高效的,我们下面给出一个图来分别计算出他们的时间复杂度。
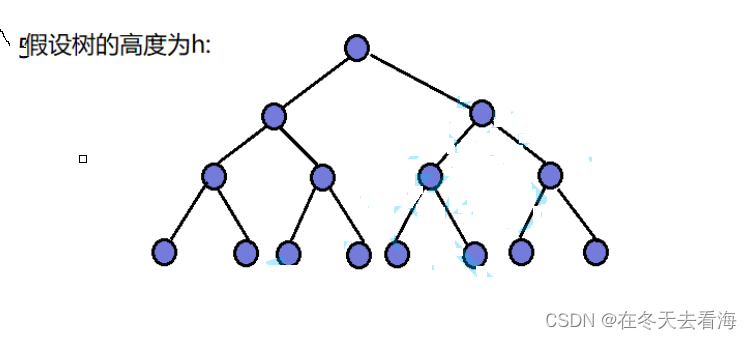
我们给出这样的一个图,首先就是假设这颗数的高度就是H,然后我们在旁边写出他们每一层的节点数。
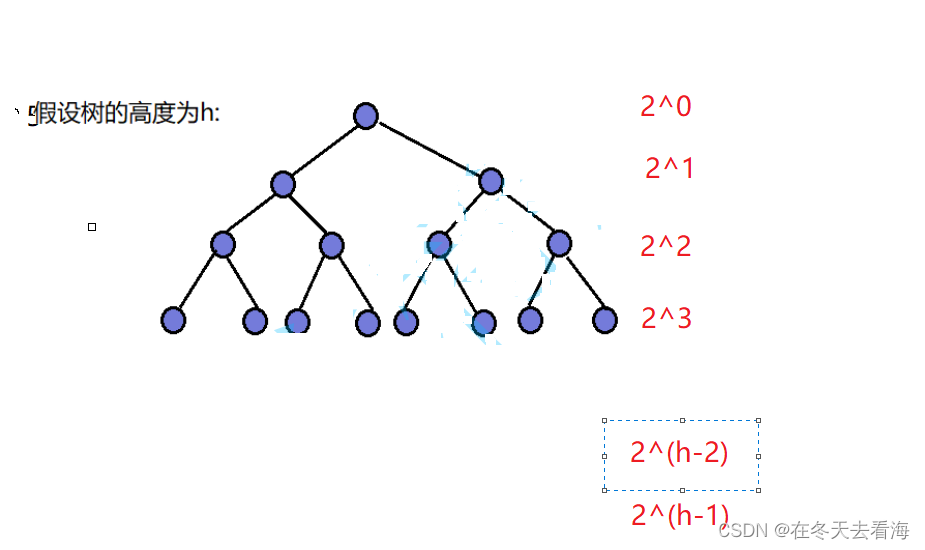
那我们可以再来计算一下他们如果是向上调整的话需要进行的调整次数。
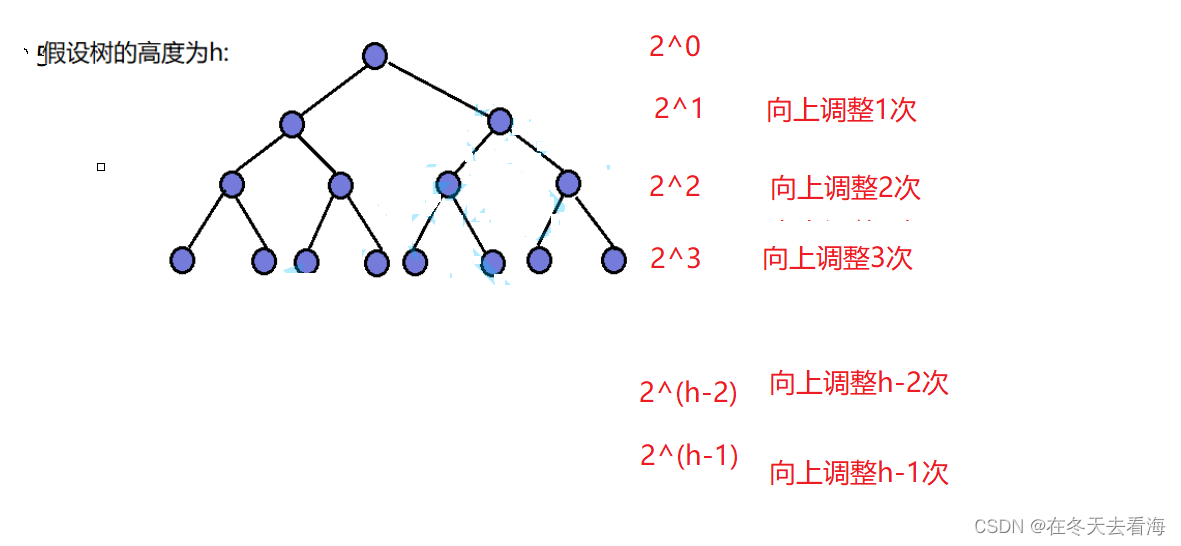
那这个时候我们只要帮他们相乘起来得到一个需要裂项相消的函数。

又因为我们的高度和我们节点个数有个等式,我们就可以把h变成N表示,我们来看看。

这个就是我们向上调整的方式,如果是向下调整的话一样的道理,只是我们是从倒数第二层开始,其实大家自己试试就行了,计算起来是一样的方法,时间复杂度是O(N)我们其实也可以通过分析得出,因为向上调整的方法是和向下的一样的,我这里就讲一个,我们不难看出向上调整的时间复杂度是高于向下的,这是为什么,我们可以看他们最多层,向上调整的时候,我们最多层是最后一层,他的节点数最多,高度也是最高的,所以是多对多,时间复杂度就是要比我们的向下调整,我们向下调整时从最后面的父亲节点开始的,而且只要调整一次就行了,这就是多对少,倒数第二层的节点基本上是整个节点的最后一个,所以我们这里得出的结论就是向下调整是最快的。我们后面就可以直接只用一个向下建堆就可以解决问题了。其实我们这里的排序本质上还是选择排序。
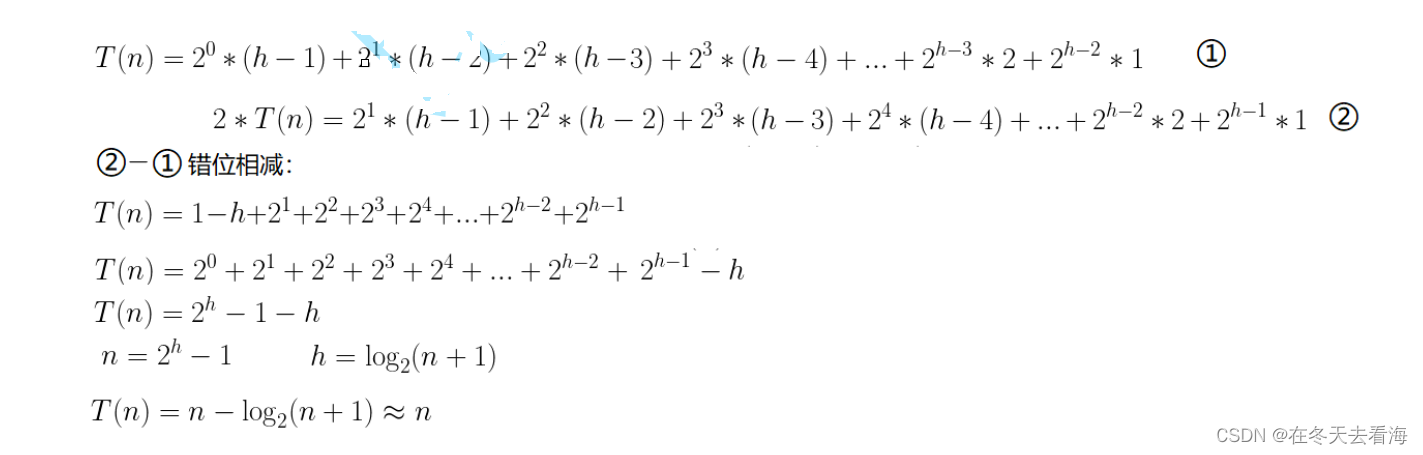
这个是向下建立堆的计算过程,大家可以看看,实在不会就私信小编,谢谢大家。
还有一个TopK问题放在下一篇文章里,因为这样流量多哈哈哈哈哈,下篇文章见。

相关文章:

数据结构——利用堆进行对数组的排序
今天文章的内容是关于我们如何利用堆的特性对我们的数组进行排序,还有就是我们的TopK的问题,这次我们放在的是文件种,我们放入一亿个数字,然后我们取出一亿个数字中最大的十个数,利用上章堆的问题进行解决。 首先就是我…...
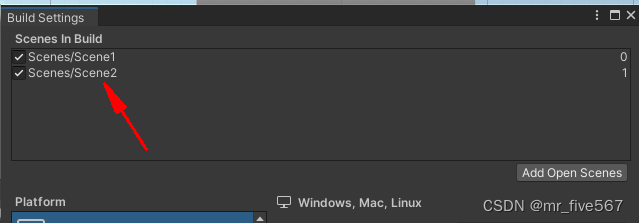
Unity 场景切换
Unity场景切换可使用以下方法: 1、SceneManager.LoadScene()方法: using UnityEngine.SceneManagement;// 切换到Scene2场景 SceneManager.LoadScene("Scene2"); 2、使用SceneManager.LoadSceneAsync()方法异步加载场景,异步加载…...

【PTA题目】7-12 N个数求和 分数 20
7-12 N个数求和 分数 20 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 本题的要求很简单,就是求N个数字的和。麻烦的是,这些数字是以有理数分子/分母的形式给出的,你输出的和也必须是有理数的形式。 输入格式: 输入第一行…...
智能AIGC写作系统ChatGPT系统源码+Midjourney绘画+支持GPT-4-Turbo模型+支持GPT-4图片对话
一、AI创作系统 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI…...

List转string 逗号分隔
List转string 逗号分隔 1、将list转化为逗号分割的字符串 String str String.join(",", list); String str StringUtils.json(list.toArray(), ","); 2、将逗号分隔的字符串转换为List List<String> list Arrays.asList(str.split("…...
手机文件怎么传到电脑?简单方法分享!
将手机文件传输到电脑可以将其备份,以防数据丢失或意外情况发生。并且电脑具有更强大的处理能力,可以将文件进行编辑、修改、转换等操作,大大提高了工作效率。那么,手机文件怎么传到电脑?本文将为大家提供简单易懂的解…...
计算机基础知识59
MySQL的卸载流程 1、先停止MySQL服务:右键“此电脑”,选择“管理”,之后选择“服务和应用程序”--“服务”,在服务中找到“MySQL”,右键选择“停止”。 2、找到“控制面板”--“程序和功能”,找到MySQL&…...

RK3568基于openharmony3.2版本之MIPI屏幕调试
mipi调试过程 1、前言2、开发环境3、调试过程3.1、下载openharmony3.2源码3.2、设备树上增加mipi-dsi屏幕的节点3.3、 分析kernel显示不出来画面3.4、 mipi屏幕显示效果图1、前言 由于工作需要,RK3568需要支持openharmony3.2系统版本,需要重新移植下载源码并且适配自家公司的…...
pycharm安装PyQt5及其工具
PyCharm安装PyQt5及其工具(Qt Designer、PyUIC、PyRcc)详细教程_pycharm pyqt5-CSDN博客 上面是原文链接,根据原文链接,我重新记录一下。IDE:pycharm 2023.2.5 一共需要安装5个。 在PyCharm中如何完整优雅地安装配置…...
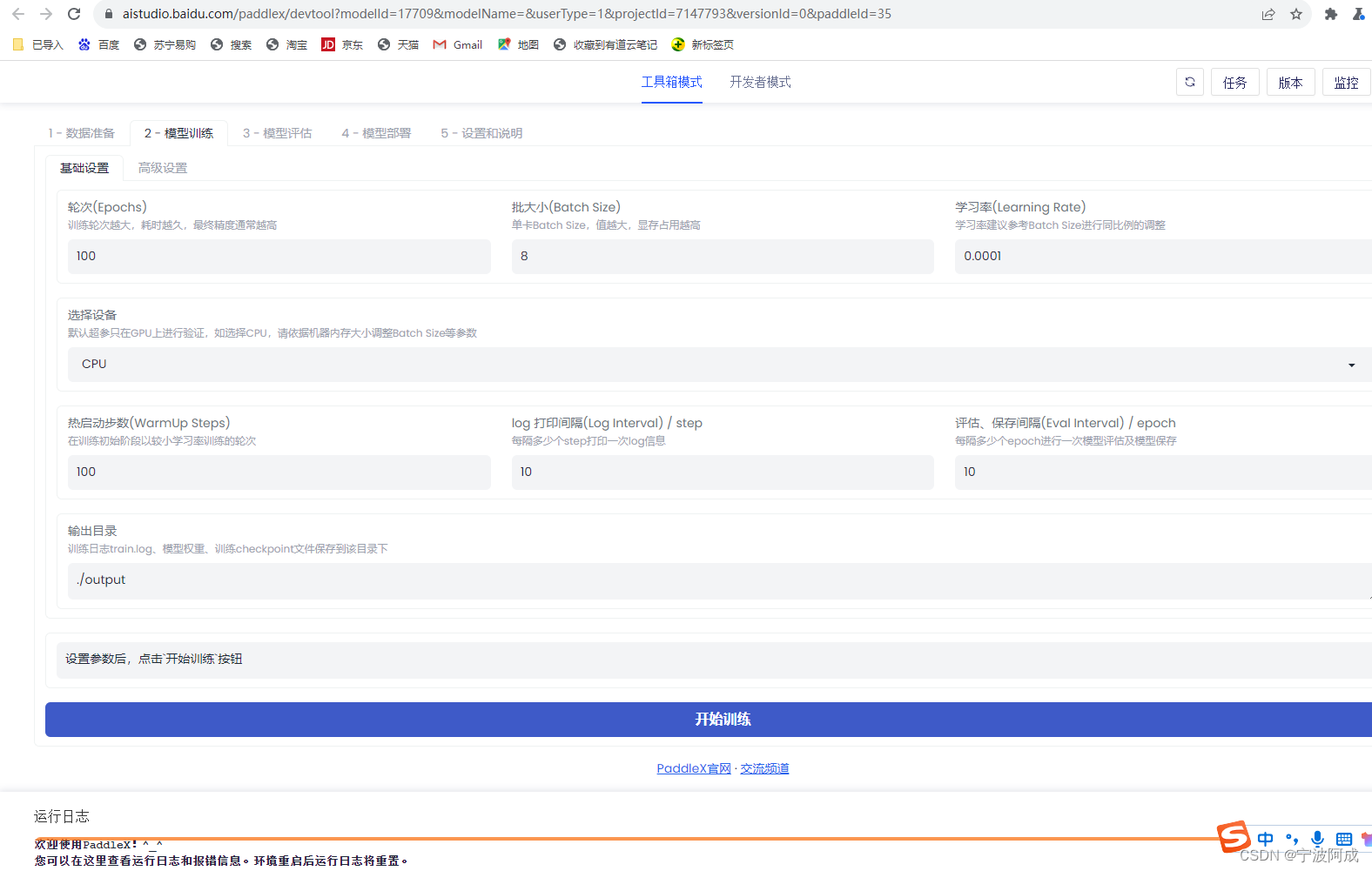
百度人工智能培训第一天笔记
参加了百度人工智能初步培训,主要是了解一下现在人工智能的基本情况,以便后续看可以参与一些啥? 下面就有关培训做一些记录,以便后续可以继续学习。 一、理论基础部分 二、实际操作部分 主要学习的百度人工智能平台如下…...

阿里云ACE认证之国际版与国内版对比!
大厂疯狂裁员,互联网行业迎来寒冬,技术人员被动陷入疯狂内卷。在愈加内卷的IT领域,“云计算”作为少有的蓝海,无疑是打工人未来实现职场提升、摆脱内卷的绝佳选择! 对于云计算行业的人来说,最值得考的肯定是…...
Java 简易版王者荣耀
所有包和类 GameFrame类 package newKingOfHonor;import java.awt.*; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.event.KeyAdapter; import java.awt.event.KeyEvent; import java.io.File; import java.util.ArrayList;im…...

【Linux】 file命令使用
file命令 file命令用于辨识文件类型。 语法 file [参数] [文件名] who命令 -Linux手册页 命令选项及作用 执行令 file --help 执行命令结果 参数 -b 列出辨识结果时,不显示文件名称;-i:显示MIME类型;-z:对…...

MFC设置单选按钮点击自己可以可选和不可选
mfc是c的一个框架,可谓是经久不衰。最近博主遇到一个问题,就是单选按钮点击自己可以设置可选和不可选,貌似类似复选框一样,但领导分发的任务上要求的是用单选按钮实现复选框这种类似功能,实现效果类似如下图࿱…...

【数据结构】二叉树之链式结构
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 一、前置说明二、二叉树的遍历2.1 前序遍历2.2 中序遍历2.3 后序遍历2.4 层序遍历 三、…...

完美的输出打印 SQL 及执行时长[MyBatis-Plus系列]
导读 Hi,大家好,我是悟纤。过着爱谁谁的生活,活出不设限的人生。 在我们日常开发工作当中,避免不了查看当前程序所执行的SQL语句,以及了解它的执行时间,方便分析是否出现了慢SQL问题。 MyBatis-Plus提供了两种SQL分析打印的方式,用于输出每条SQL语句及其执行时间,针…...
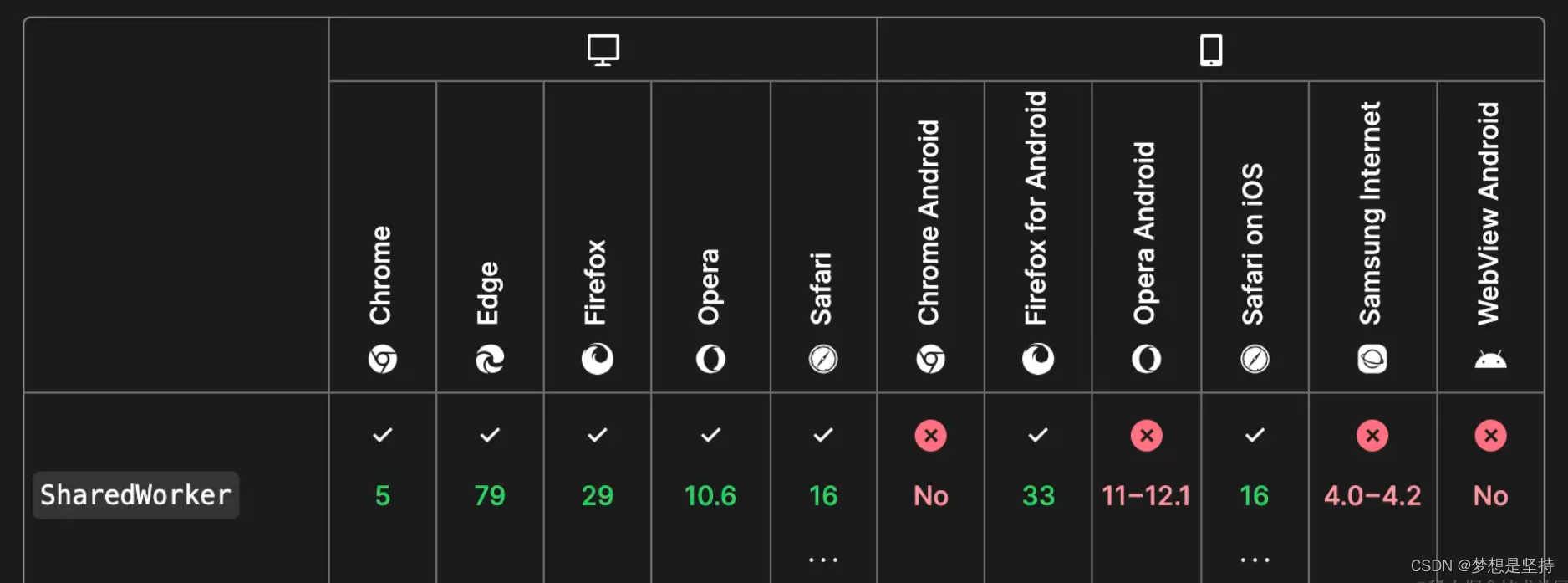
跨标签页通信的8种方式(下)
跨标签页通信是指在浏览器中的不同标签页之间进行数据传递和通信的过程。在传统的Web开发中,每个标签页都是相互独立的,无法直接共享数据。然而,有时候我们需要在不同的标签页之间进行数据共享或者实现一些协同操作,这就需要使用跨…...

笔记二十、使用路由Params进行传递参数
20.1、在父组件中设置路由参数 <NavLink to{classify/${this.state.name}} className{this.activeStyle}>classify</NavLink> 父组件 Home/index.jsx import React from "react"; import {NavLink, Outlet} from "react-router-dom";class Ap…...

K8S----taint、tolerations、label
一、污点(taint),针对的是节点,只有node才有污点的概念 1、 给节点增加一个污点 kubectl taint nodes node1 key1=value1:NoSchedule给节点 node1 增加一个污点,它的键名是 key1,键值是 value1,效果是 NoSchedule。 这表示只有拥有和这个污点相匹配的容忍度的 Pod 才能…...
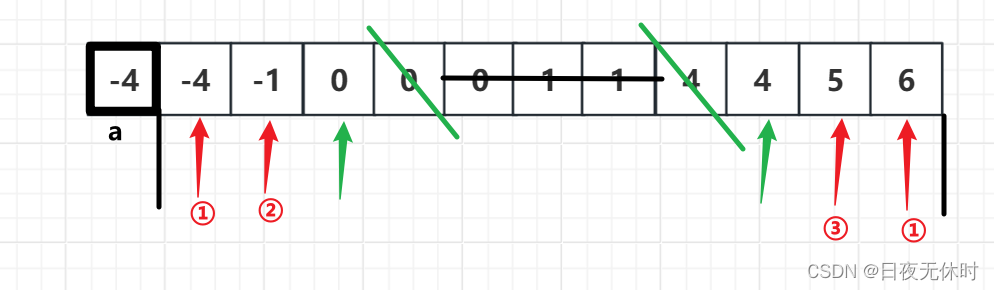
【双指针】三数之和
三数之和 在做这道题之前,建议建议先将两数之和做完再做,提升更大~ 文章目录 三数之和题目描述算法原理解法一解法二思路如下:处理细节问题: 代码编写Java代码编写C代码编写 15. 三数之和 - 力扣(LeetCode࿰…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
