C语言——打印出所有的“水仙花数”
所谓水仙花数,是指一个3位数,其各位数字立方和等于该数本身。水仙花数是指一个三位数,它的每个位上的数字的立方和等于它本身。例如,153是一个水仙花数,因为1^3 + 5^3 + 3^3 = 153。
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
int main()
{int i, j, k, num;// 循环遍历所有的3位数for (i = 1; i <= 9; i++) {for (j = 0; j <= 9; j++) {for (k = 0; k <= 9; k++) {num = i * 100 + j * 10 + k;// 判断是否为水仙花数并打印if (num == i*i*i + j*j*j + k*k*k) {printf("%d\n", num);}}}}return 0;
} 这个程序通过三个嵌套的循环遍历所有的3位数,并检查它们是否满足水仙花数的条件。如果一个数满足条件,它就会被打印出来。
这个程序通过三个嵌套的循环遍历所有的3位数,并检查它们是否满足水仙花数的条件。如果一个数满足条件,它就会被打印出来。
相关文章:

C语言——打印出所有的“水仙花数”
所谓水仙花数,是指一个3位数,其各位数字立方和等于该数本身。水仙花数是指一个三位数,它的每个位上的数字的立方和等于它本身。例如,153是一个水仙花数,因为1^3 5^3 3^3 153。 #define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>…...

<HarmonyOS第一课>应用程序框架 【课后考核】
【习题】应用程序框架 判断题 一个应用只能有一个UIAbility。错误(False)创建的Empty Ability模板工程,初始会生成一个UIAbility文件。正确(True)每调用一次router.pushUrl()方法,页面路由栈数量均会加1。错误(False) 单选题 API9及以上,r…...
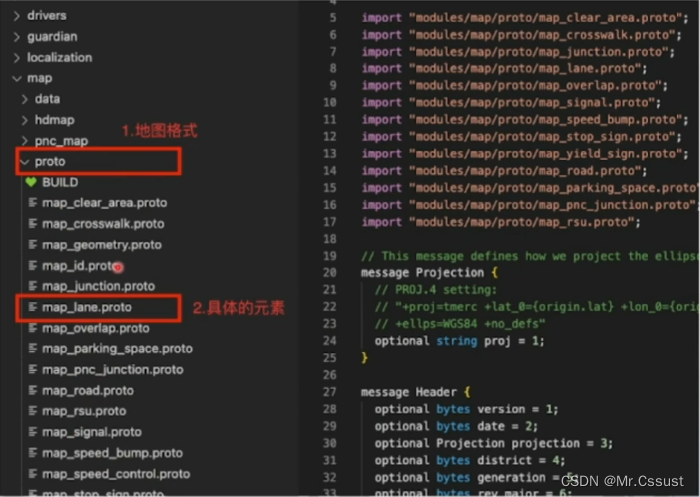
自动驾驶学习笔记(十一)——高精地图
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《Apollo Beta宣讲和线下沙龙》免费报名—>传送门 文章目录 前言 高精地图 地图采集 底图制作 地图…...
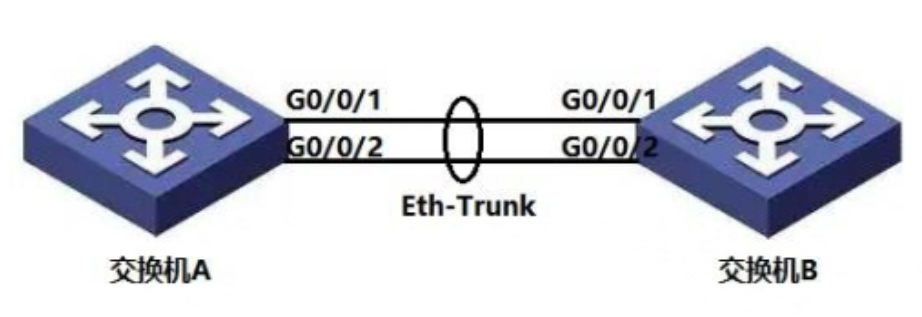
HCIA-H12-811题目解析(2)
1、【单选题】 在以太网这种多点访问网络上PPPOE服务器可以通过一个以太网端口与很多PPPOE客户端建立起PPP连接,因此服务器必须为每个PPP会话建立唯一的会话标识符以区分不同的连接PPPOE会使用什么参数建立会话标识符? 2、【单选题】PPP协议定义的是OSI参考模型中…...

Docker-简介、基本操作
目录 Docker理解 1、Docker本质 2、Docker与虚拟机的区别 3、Docker和JVM虚拟化的区别 4、容器、镜像的理解 5、Docker架构 Docker客户端 Docker服务器 Docker镜像 Docker容器 镜像仓库 Docker基本操作 1、Docker镜像仓库 镜像仓库分类 镜像仓库命令 docker lo…...
(C dp D gcd 分解+容斥 E tarjan+dp))
Codeforces Round 911 (Div. 2)(C dp D gcd 分解+容斥 E tarjan+dp)
A.手玩题: 可以通过最后一个样例,如果是长度为3的连续O,直接在两边放就行,然后一直用中间的水填到其他地方 #include<bits/stdc.h> using namespace std; const int N 3e510,mod 998244353; #define int long long int n…...

给csgo游戏搬砖新手的十大建议
1、不要参与赌博性质的开箱和炼金,因为真的会上瘾,赚了还好,亏了你得哭。 2、实在想要玩饰品,直接去悠悠有品或者网易buff看价格,底价再砍10元,总会有人愿意卖的。 3、在steam上不要接受陌生人的好友申请…...
预习报告)
西南科技大学模拟电子技术实验一(常用电子仪器的使用及电子元器件的识别)预习报告
一、计算/设计过程 说明:本实验是验证性实验,计算预测验证结果。是设计性实验一定要从系统指标计算出元 1、用万用表电阻挡测量实验板(箱)上电位器(可调电阻)的参数范围。 0~1kΩ电阻: 1k*0%=0 1k*100%=1k 所以范围为0~1k 0~10kΩ电阻: 10k*0%=0 10k*…...
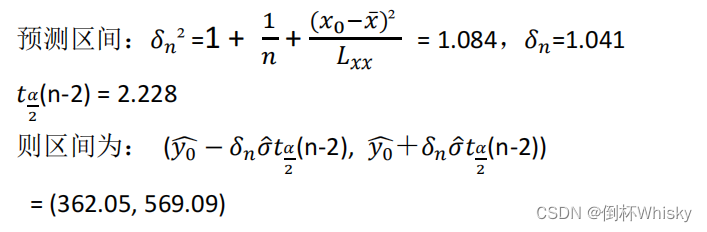
回归分析例题(多元统计分析期末复习)
例一 例二 一元线性回归 解: (1)y a ^ \hat{a} a^ b ^ \hat{b} b^x,求线性回归方程即求出 a ^ \hat{a} a^和 b ^ \hat{b} b^ 而 b ^ \hat{b} b^ L x y L x x { {L_{xy}} \over {L_{xx}} } LxxLxy 所以我们首先需要计算 L x…...
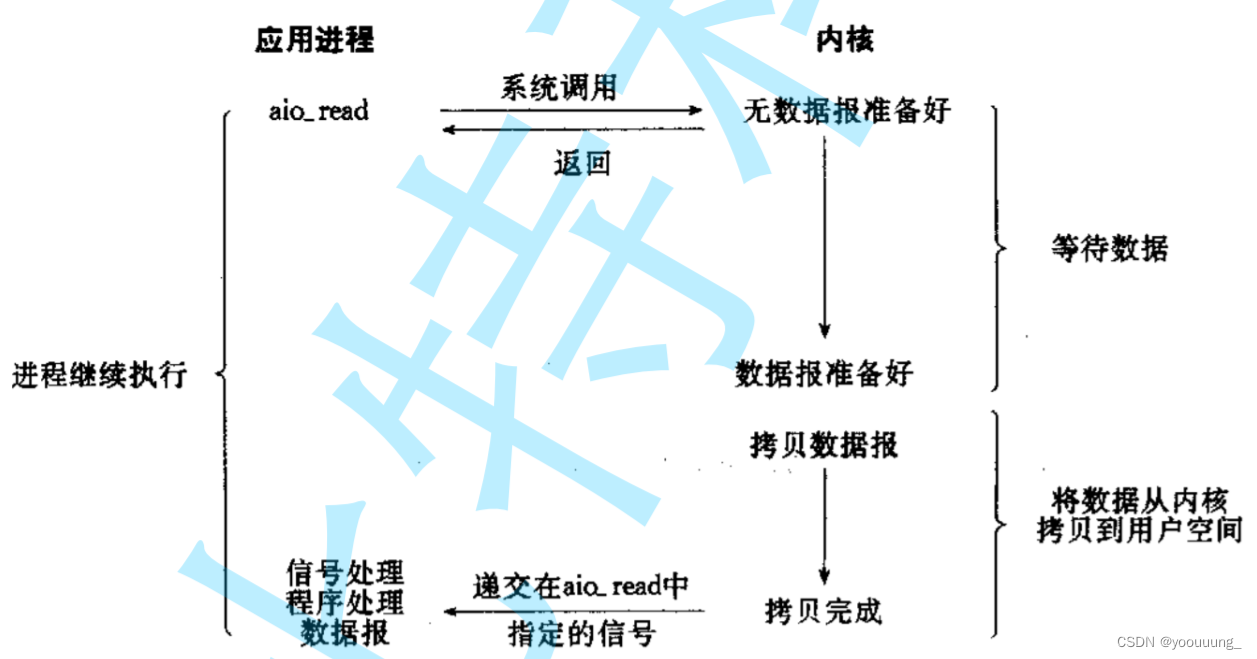
Linux多路转接select,poll
文章目录 目录 文章目录 一、五种IO模型 1.阻塞IO: 2.非阻塞IO 3.信号驱动IO 4.IO多路转接 5.异步IO 二、高级IO的一些重要概念 1.同步通信和异步通信 2.阻塞和非阻塞 三、其他高级IO 四、非阻塞IO 1.fctl函数 2.实现setNoBlock函数,将文件描述符设置…...
如何轻松将 4K 转换为 1080p 高清视频
由于某些原因,你可能有一些 4K 视频,与1080p、1080i、720p、720i等高清视频相比,4K 视频具有更高的分辨率,可以给您带来更多的视觉和听觉享受。但是,播放4k 视频是不太容易的,因为超高清电视没有高清电视那…...
)
责任链模式 (Chain of Responsibility Pattern)
定义 责任链模式是一种行为型设计模式,用于在对象间建立一条处理请求的链。它允许多个对象有机会处理请求,从而减少请求的发送者和接收者之间的耦合。在责任链模式中,每个接收者包含对另一个接收者的引用,形成一条链。如果一个对…...
企业营销管理能够实现自动化吗?怎么做?
当今企业面临着越来越多的营销难题:如何有效培育潜在客户、如何提高营销活动的效果、如何优化营销资源的分配......企业的营销管理怎么做?或许CRM系统营销自动化会起到作用。 客户细分: 企业可以通过CRM的客户细分功能,根据客户…...
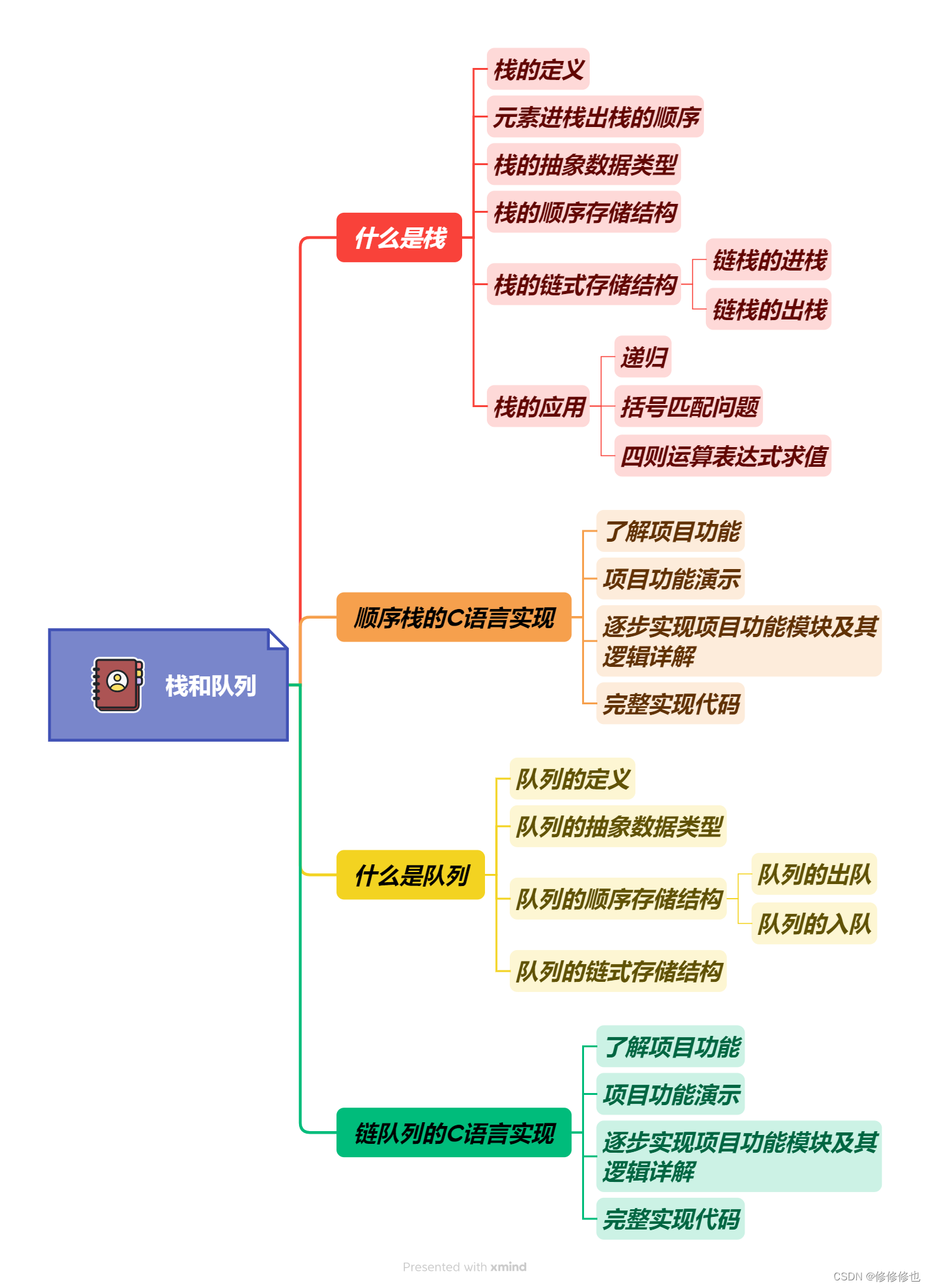
【数据结构】什么是栈?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌栈的定义 📌元素进栈出栈的顺序 📌栈的抽象数据类型 📌栈的顺序存储结构 📌栈的链式存储结构 链栈的进…...
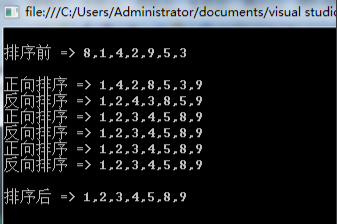
基于C#实现鸡尾酒排序(双向冒泡排序)
通俗易懂点的话,就叫“双向冒泡排序”。 冒泡是一个单向的从小到大或者从大到小的交换排序,而鸡尾酒排序是双向的,从一端进行从小到大排序,从另一端进行从大到小排序。 从图中可以看到,第一次正向比较,我们…...
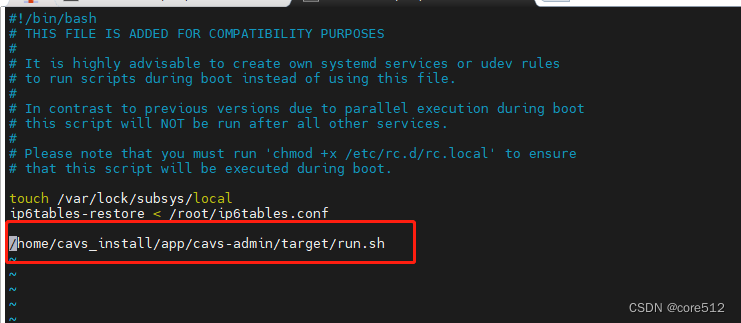
CentOS添加开机启动
1.编写项目启动脚本(run.sh) #!/bin/bash-切换到程序所在路径 cd /home/cavs_install/app/cavs-admin/target/ # 等待其他组件启动完毕后再启动本项目(如果不需要等待,本步骤可省略) sleep 300 # 实际启动命令 nohup …...
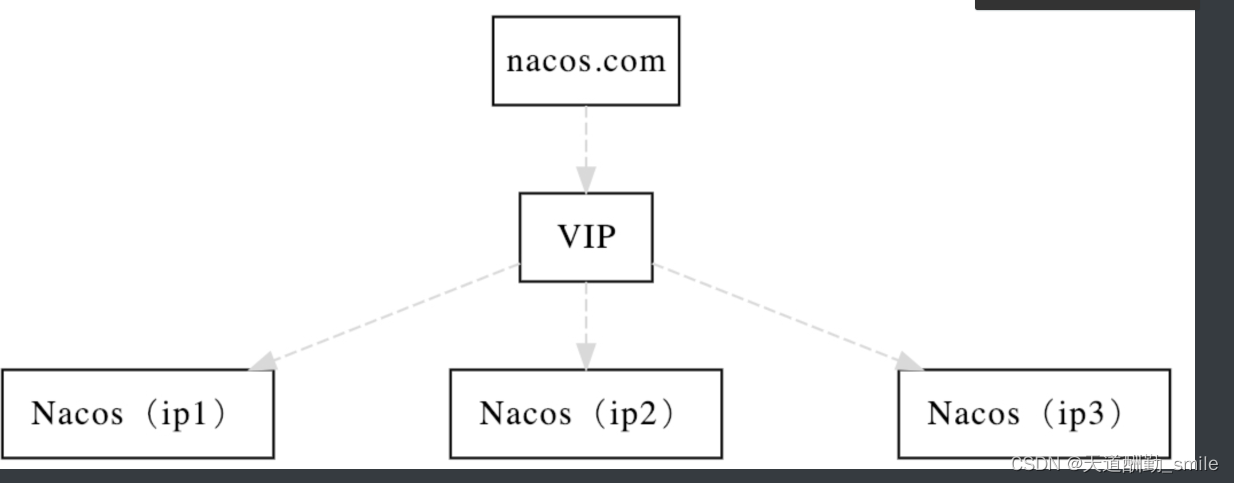
SpringCloudAlibaba之Nacos的持久化和高可用——详细讲解
目录 一、Nacos持久化 1.持久化说明 2.安装mysql数据库5.6.5以上版本(略) 3.修改配置文件 二、nacos高可用 1.集群说明 2.nacos集群架构图 2.集群搭建注意事项 3.集群规划 4.搭建nacos集群 5.安装Nginx 6.配置nginx conf配置文件 7.启动nginx进行测试即可 一、Nacos持久…...
vue3安装eslint和prettier,最简单的步骤
第1步: 安装eslint yarn add eslint -D 第2步: 在根文件夹中,创建.eslintrc.js文件 第3步: 在package.json文件中新增命令 "lint": "eslint --fix --ext .ts,.tsx,.vue src --quiet","prettier"…...

Day32| Leetcode 122. 买卖股票的最佳时机 II Leetcode 55. 跳跃游戏 Leetcode 45. 跳跃游戏 II
Leetcode 122. 买卖股票的最佳时机 II 题目链接 122 买卖股票的最佳时机 II 本题目设计的还是比较巧妙的,把最终的利润分为每天的利润就解决了(贪心),每天的利润就是前一天买进,后一天卖出,转化到代码上就…...
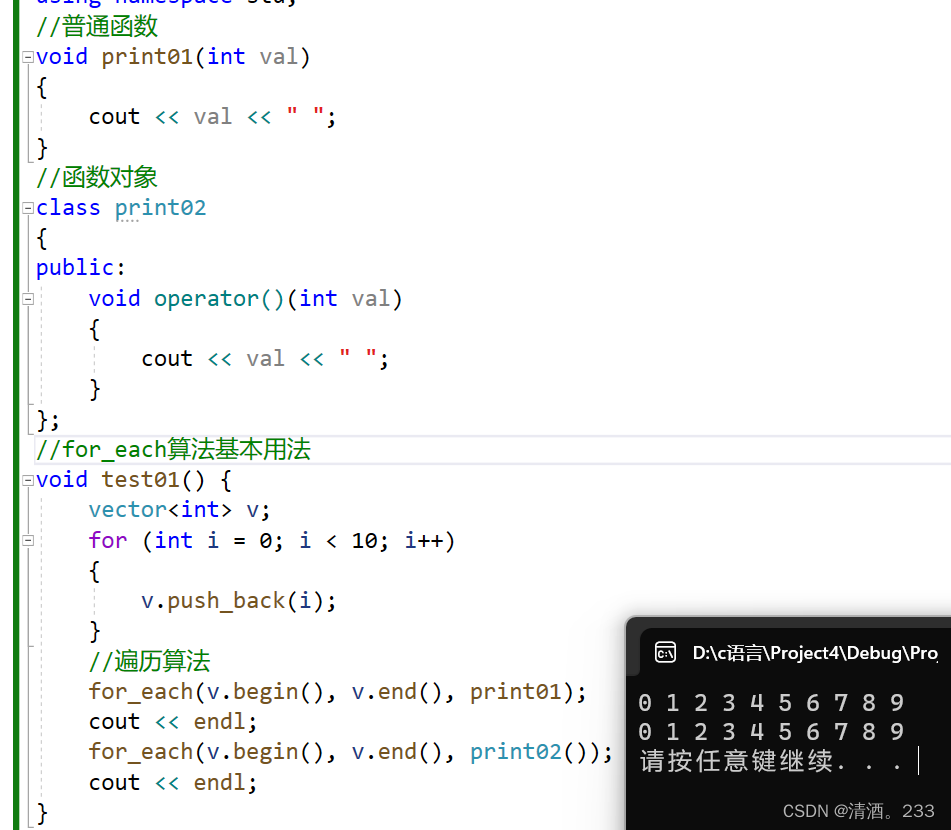
95.STL-遍历算法 for_each
算法概述: 算法主要是由头文件 <algorithm> <functional> <numeric> 组成。 <algorithm> 是所有STL头文件中最大的一个,范围涉及到比较、 交换、查找、遍历操作、复制、修改等等 <numeric> 体积很小,只包括几个在序列上面…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
