Codeforces Round 911 (Div. 2)(C dp D gcd 分解+容斥 E tarjan+dp)
A.手玩题:
可以通过最后一个样例,如果是长度为3的连续O,直接在两边放就行,然后一直用中间的水填到其他地方
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod= 998244353;
#define int long long
int n,m,k;void solve()
{cin>>n;string s;cin>>s;s="?"+s;int res=0;int now=0;s+="#";for(int i=1;i<=n+1;i++){if(s[i]=='#'){if(now>=3){cout<<2<<"\n";return ;}res+=min(2ll,now);now=0;}else now++;}cout<<res<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}B:
直接每个数字都去判定能不能成为最后一个
假设都变成 a
然后目标变成 让 b c的数量相同
假设只操作b c,那么他们的差都减一,差奇偶性不变
如果操作a c或者a b,那么他们的差还是不变,因为-b -a ,+c,差变化2
所以如果差是奇数没法操作,
再想一下,那么对a的数量有没有啥要求呢
可以发现没要求,
因为b c可以操作自己变出一个a,然后再用 a去操作自己,他们可以独立自主
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod= 998244353;
#define int long long
int n,m,k;void solve()
{int a,b,c;auto ok=[&](int a,int b,int c){int need=abs(b-c);if(need%2==0) return true;return false;};cin>>a>>b>>c;if(ok(a,b,c)) cout<<"1 ";else cout<<"0 "; if(ok(b,a,c)) cout<<"1 ";else cout<<"0 "; if(ok(c,a,b)) cout<<"1 ";else cout<<"0 "; cout<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}C:
感觉很裸的dp
dp状态:通过u这个子树到达叶子节点的最少次数
那么如果是叶子节点无需代价
如果不是叶子节点,判断走的左右子树的方向和当前根方向是否相同,不同代价+1
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod= 998244353;
#define int long long
typedef long long LL;
typedef pair<int, char> PII;int n,m,k;
string s;
vector<PII> g[N];
int f[N];
void dfs(int u){//if(s[u]=='U') f[u]=1;if(g[u].empty()){f[u]=0;return ;}for(auto [v,w]:g[u]){dfs(v);f[u]=min(f[u],f[v]+(w!=s[u]));}
}
void solve()
{cin>>n>>s;s="?"+s;for(int i=1;i<=n;i++){g[i].clear();f[i]=2e18;}for(int i=1;i<=n;i++){int a,b;cin>>a>>b;if(a) g[i].emplace_back(a,'L');if(b) g[i].emplace_back(b,'R');}dfs(1);cout<<f[1]<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}D:
首先先排序,排序不影响答案
然后问题变成了
当前数(a[i]和前面数的gcd之和)*后面的个数(就是k嘛)
然后难点是前面
我们可以分开求a[x]的因数的贡献,
通过一个调和级数求1到10w的每个数的因子(不是质因子哦,而是因子,比如16的因子有1 2 4 8 16)
然后a[i]和前面数因子的贡献计算
这里举例说明一下
假设
a[i]=20 a[j]=4
a[i]的因子有 1 2 4 510 20
a[j]因子有 1 2 4
那么他们gcd的贡献是gcd(20,4)=4
直接求他们里面最大的共同的的因子不好求(n^2超时间嘛)
但是我们知道每个数的因子最多就128个? n*128够了
然后我们可以求当前数的当前因子能和前面数的因子的总贡献
比如上面例子的1和1配对 2和2配对 4和4配对
但是注意到我们贡献其实只有一个4
那么咋办呢可以用容斥来解决
4的因子里面有2 1
2的因子有1
1的因子只有自己
所以我们求完后还要减去这个因子的倍数
设当前数组f[x]表示因子x有多少个(i,j)的对数
根据上面那个例子a[i]=20 a[j]=4
f[4]=1 f[2]=1 f[1]=1(因为只有两个数嘛,所以只有一对)
然后计算完这个f数组,我们要用容斥减去当前x的倍数的对数
比如上面例子的f[2]要减去f[4] f[1]要减去f[1]减去f[2]减去f[4](这里的f[2]要先减去f[4]哦)
然后当前f[x]数组就是名副其实的因子是x的对数
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10,mod= 998244353;
#define int long long
typedef long long LL;
typedef pair<int, char> PII;int n,m,k;
int a[N];
vector<int> g[N];
int gcd(int a,int b){return b?gcd(b,a%b):a;
}
void init(){for(int i=1;i<N;i++){for(int j=i;j<N;j+=i){g[j].push_back(i);}}
}
void solve()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}sort(a+1,a+1+n);vector<int> c(N),f(N);for(int i=1;i<=n;i++){for(auto x:g[a[i]]){f[x]+=c[x]*(n-i);c[x]++;}}int res=0;for(int i=100000;i>=1;i--){for(int j=i+i;j<=100000;j+=i){f[i]-=f[j];}res+=f[i]*i;}cout<<res<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;init();cin>>t;while(t--) solve();
}E:
手完可以发现如果是强联通分量最后会变成一个有向完全图
代表着如果进来了,因为要求路径最长,所以这个强联通分量的点都要走一遍且保证点不重复,
然后直接dp一下即可
然后因为是拓扑序大的 scc_cnt小,因为tarjan是先到底部的,底部的点会先缩,再回溯到上面缩,所以dp直接从1开始即可
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod= 998244353;
#define int long long
typedef long long LL;
typedef pair<int, char> PII;int n,m,k;vector<int> g[N],h[N];
int dfn[N],low[N];
int scc_cnt,timestamp;
int stk[N],id[N];
bool in_stk[N];
int sz[N];
int top;
stack<int> s;
int b[N],a[N],c[N],f[N],gg[N];
void tarjan(int u){dfn[u] = low[u] = ++ timestamp;stk[ ++ top] = u, in_stk[u] = true;for (auto j:g[u]){if (!dfn[j]){tarjan(j);low[u] = min(low[u], low[j]);}else if (in_stk[j]) low[u] = min(low[u], dfn[j]);}if (dfn[u] == low[u]){++ scc_cnt;int y;do {y = stk[top -- ];in_stk[y] = false;id[y] = scc_cnt;} while (y != u);}}
void solve()
{cin>>n>>m;scc_cnt=timestamp=top=0;for(int i=0;i<=n;i++){g[i].clear();dfn[i]=low[i]=0;in_stk[i]=false;h[i].clear();id[i]=b[i]=c[i]=0;f[i]=gg[i]=0;}for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=m;i++){int a,b;cin>>a>>b;g[a].push_back(b);}for(int i=1;i<=n;i++){if(!dfn[i])tarjan(i);}for(int i=1;i<=n;i++){b[id[i]]+=a[i];c[id[i]]++;}for(int u=1;u<=n;u++){//cout<<id[u]<<" ";for(auto v:g[u]){if(id[u]!=id[v]){h[id[u]].push_back(id[v]);}}}int ans1=0,ans2;for(int i=1;i<=scc_cnt;i++){f[i]=c[i],gg[i]=b[i];for(auto j:h[i]){int t1=f[j]+c[i],t2=gg[j]+b[i];if(t1>f[i]||t1==f[i]&&t2<gg[i]){f[i]=t1,gg[i]=t2;}}if (f[i] > ans1 || f[i] == ans1 && gg[i] < ans2) ans1 = f[i], ans2 = gg[i];}cout<<ans1<<" "<<ans2<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}相关文章:
(C dp D gcd 分解+容斥 E tarjan+dp))
Codeforces Round 911 (Div. 2)(C dp D gcd 分解+容斥 E tarjan+dp)
A.手玩题: 可以通过最后一个样例,如果是长度为3的连续O,直接在两边放就行,然后一直用中间的水填到其他地方 #include<bits/stdc.h> using namespace std; const int N 3e510,mod 998244353; #define int long long int n…...

给csgo游戏搬砖新手的十大建议
1、不要参与赌博性质的开箱和炼金,因为真的会上瘾,赚了还好,亏了你得哭。 2、实在想要玩饰品,直接去悠悠有品或者网易buff看价格,底价再砍10元,总会有人愿意卖的。 3、在steam上不要接受陌生人的好友申请…...
预习报告)
西南科技大学模拟电子技术实验一(常用电子仪器的使用及电子元器件的识别)预习报告
一、计算/设计过程 说明:本实验是验证性实验,计算预测验证结果。是设计性实验一定要从系统指标计算出元 1、用万用表电阻挡测量实验板(箱)上电位器(可调电阻)的参数范围。 0~1kΩ电阻: 1k*0%=0 1k*100%=1k 所以范围为0~1k 0~10kΩ电阻: 10k*0%=0 10k*…...
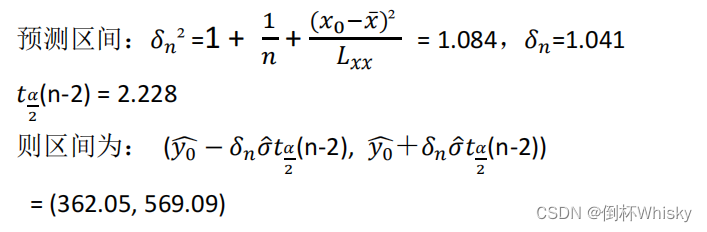
回归分析例题(多元统计分析期末复习)
例一 例二 一元线性回归 解: (1)y a ^ \hat{a} a^ b ^ \hat{b} b^x,求线性回归方程即求出 a ^ \hat{a} a^和 b ^ \hat{b} b^ 而 b ^ \hat{b} b^ L x y L x x { {L_{xy}} \over {L_{xx}} } LxxLxy 所以我们首先需要计算 L x…...
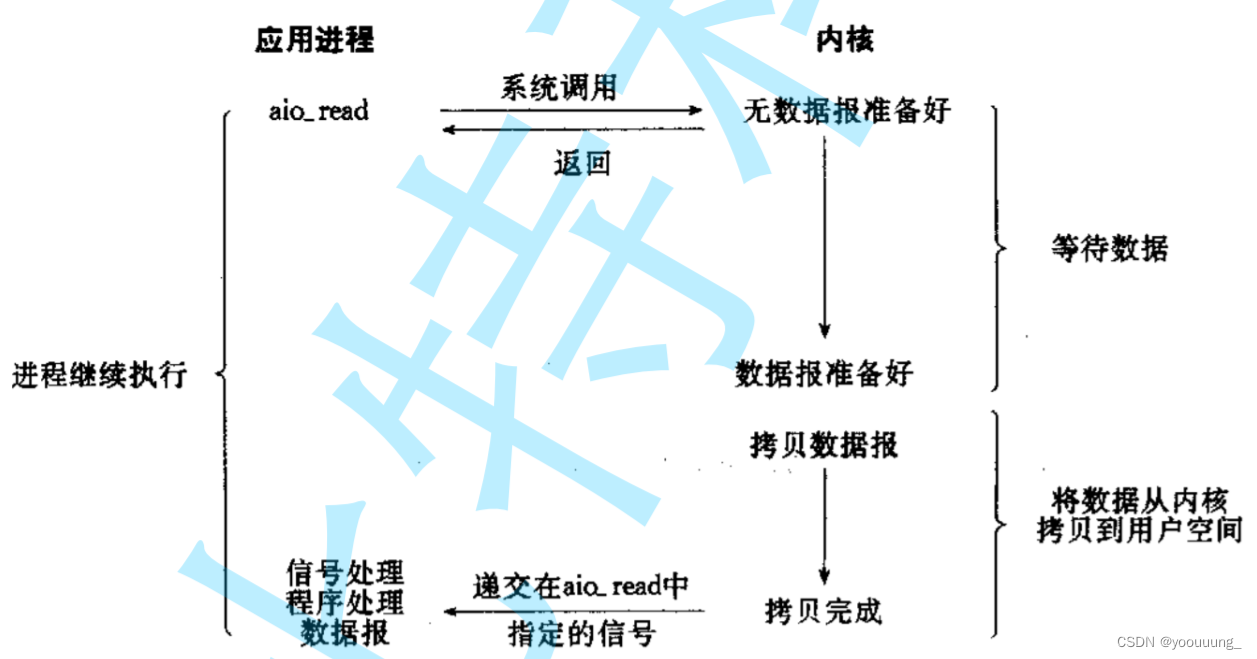
Linux多路转接select,poll
文章目录 目录 文章目录 一、五种IO模型 1.阻塞IO: 2.非阻塞IO 3.信号驱动IO 4.IO多路转接 5.异步IO 二、高级IO的一些重要概念 1.同步通信和异步通信 2.阻塞和非阻塞 三、其他高级IO 四、非阻塞IO 1.fctl函数 2.实现setNoBlock函数,将文件描述符设置…...
如何轻松将 4K 转换为 1080p 高清视频
由于某些原因,你可能有一些 4K 视频,与1080p、1080i、720p、720i等高清视频相比,4K 视频具有更高的分辨率,可以给您带来更多的视觉和听觉享受。但是,播放4k 视频是不太容易的,因为超高清电视没有高清电视那…...
)
责任链模式 (Chain of Responsibility Pattern)
定义 责任链模式是一种行为型设计模式,用于在对象间建立一条处理请求的链。它允许多个对象有机会处理请求,从而减少请求的发送者和接收者之间的耦合。在责任链模式中,每个接收者包含对另一个接收者的引用,形成一条链。如果一个对…...
企业营销管理能够实现自动化吗?怎么做?
当今企业面临着越来越多的营销难题:如何有效培育潜在客户、如何提高营销活动的效果、如何优化营销资源的分配......企业的营销管理怎么做?或许CRM系统营销自动化会起到作用。 客户细分: 企业可以通过CRM的客户细分功能,根据客户…...
【数据结构】什么是栈?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌栈的定义 📌元素进栈出栈的顺序 📌栈的抽象数据类型 📌栈的顺序存储结构 📌栈的链式存储结构 链栈的进…...
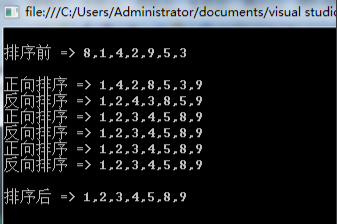
基于C#实现鸡尾酒排序(双向冒泡排序)
通俗易懂点的话,就叫“双向冒泡排序”。 冒泡是一个单向的从小到大或者从大到小的交换排序,而鸡尾酒排序是双向的,从一端进行从小到大排序,从另一端进行从大到小排序。 从图中可以看到,第一次正向比较,我们…...
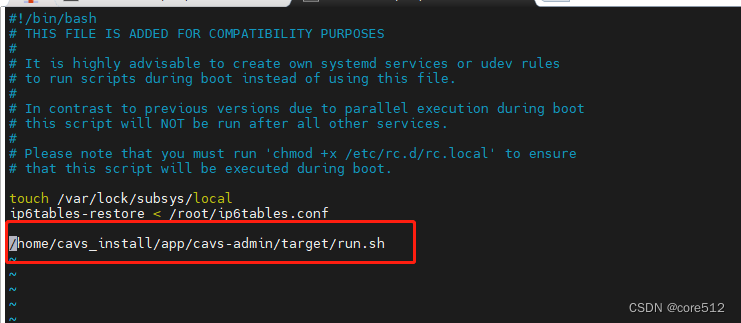
CentOS添加开机启动
1.编写项目启动脚本(run.sh) #!/bin/bash-切换到程序所在路径 cd /home/cavs_install/app/cavs-admin/target/ # 等待其他组件启动完毕后再启动本项目(如果不需要等待,本步骤可省略) sleep 300 # 实际启动命令 nohup …...
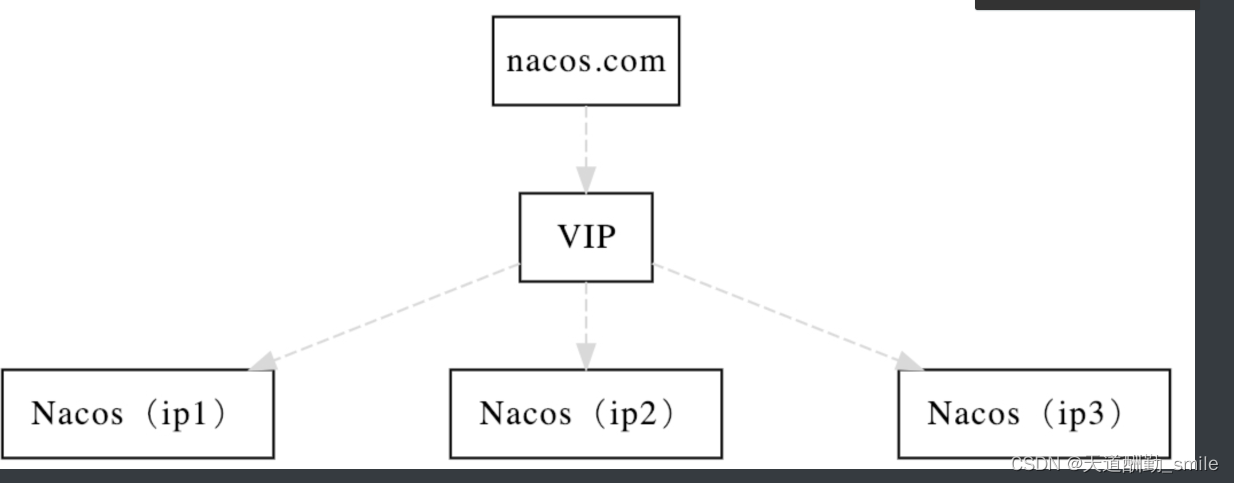
SpringCloudAlibaba之Nacos的持久化和高可用——详细讲解
目录 一、Nacos持久化 1.持久化说明 2.安装mysql数据库5.6.5以上版本(略) 3.修改配置文件 二、nacos高可用 1.集群说明 2.nacos集群架构图 2.集群搭建注意事项 3.集群规划 4.搭建nacos集群 5.安装Nginx 6.配置nginx conf配置文件 7.启动nginx进行测试即可 一、Nacos持久…...
vue3安装eslint和prettier,最简单的步骤
第1步: 安装eslint yarn add eslint -D 第2步: 在根文件夹中,创建.eslintrc.js文件 第3步: 在package.json文件中新增命令 "lint": "eslint --fix --ext .ts,.tsx,.vue src --quiet","prettier"…...

Day32| Leetcode 122. 买卖股票的最佳时机 II Leetcode 55. 跳跃游戏 Leetcode 45. 跳跃游戏 II
Leetcode 122. 买卖股票的最佳时机 II 题目链接 122 买卖股票的最佳时机 II 本题目设计的还是比较巧妙的,把最终的利润分为每天的利润就解决了(贪心),每天的利润就是前一天买进,后一天卖出,转化到代码上就…...
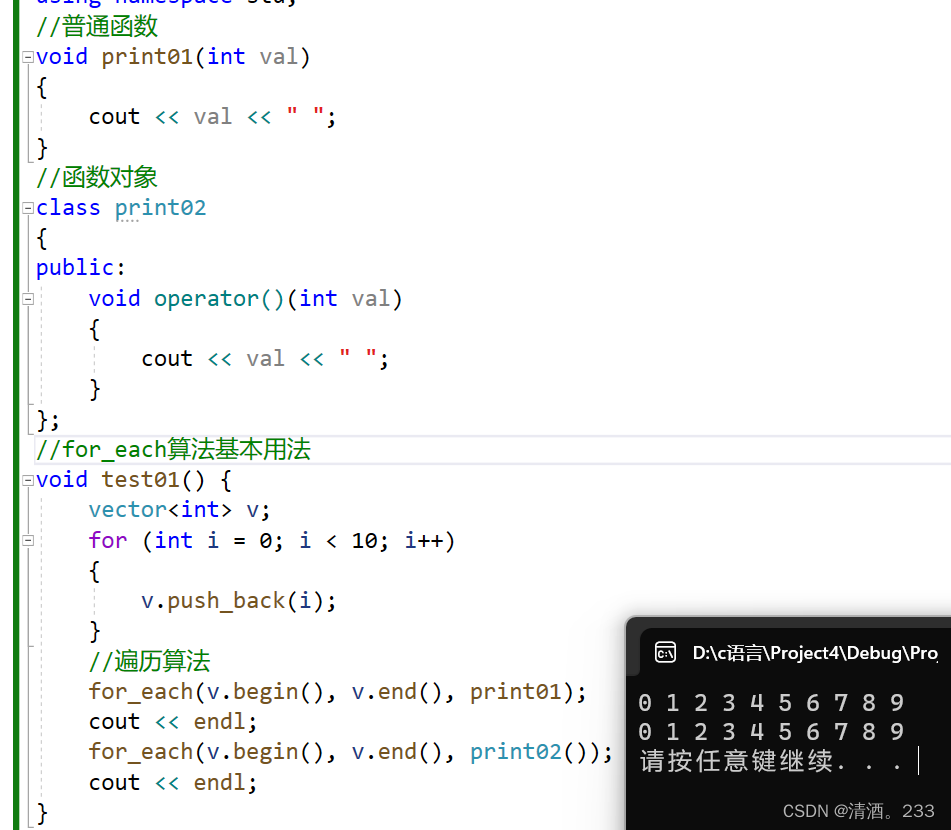
95.STL-遍历算法 for_each
算法概述: 算法主要是由头文件 <algorithm> <functional> <numeric> 组成。 <algorithm> 是所有STL头文件中最大的一个,范围涉及到比较、 交换、查找、遍历操作、复制、修改等等 <numeric> 体积很小,只包括几个在序列上面…...

Python基础语法之学习type()函数
Python基础语法之学习type函数 一、代码二、效果 查看数据类型或者说查看变量存储的数据类型 一、代码 print(type("文本")) print(type(666)) print(type(3.14))二、效果 梦想是生活的指南针,坚持追逐梦想,终将抵达成功的彼岸。不要害怕失败…...

filebeat报错dropping too large message of size
filebeat报错: dropping too large message of size 1714620. 原因: kafka对每一条消息的大小进行了限制。 解决 kafka端 修改config/server.properties,添加以下配置 max_message_bytes10000000 replica.fetch.max.bytes10000000修改…...
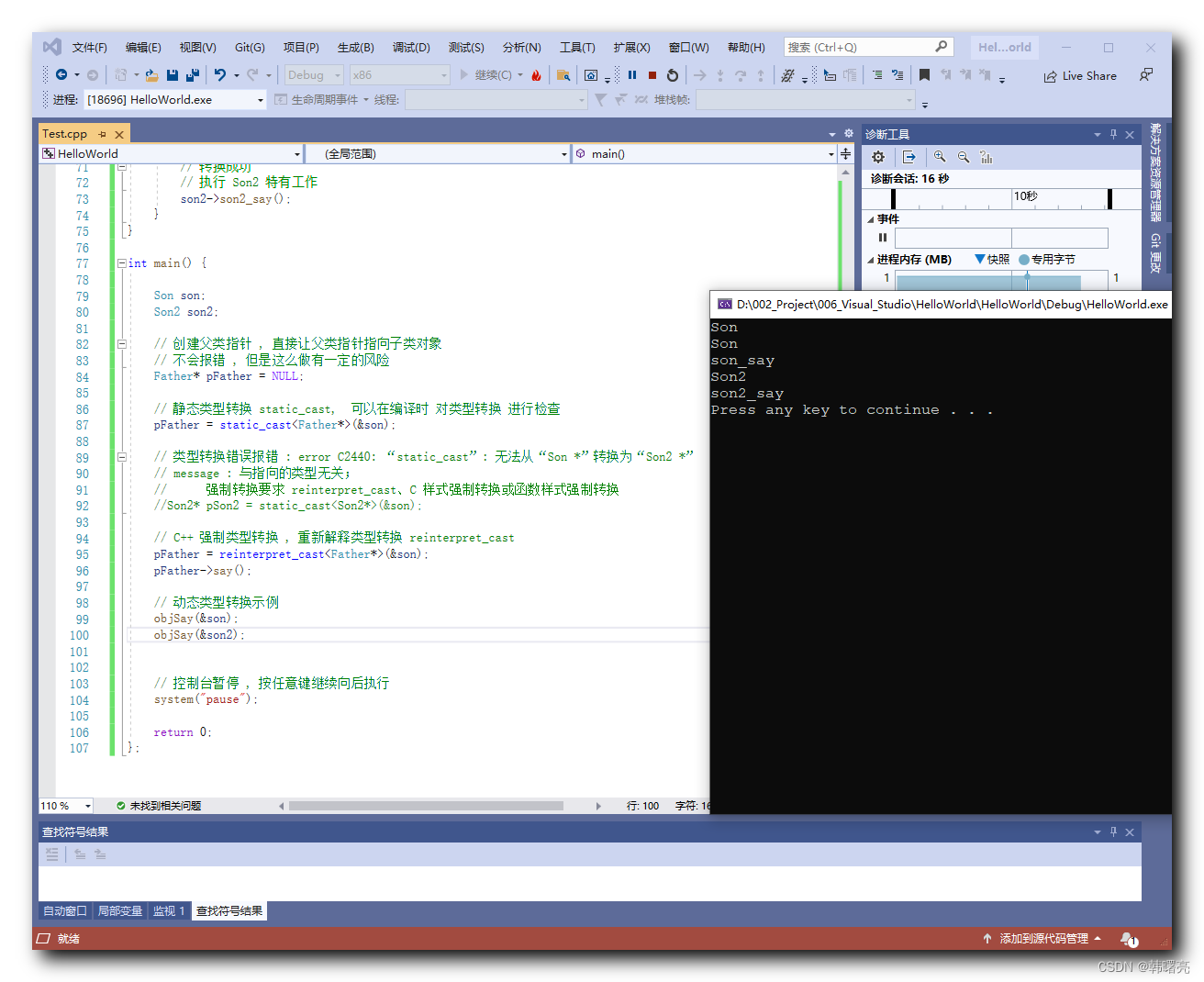
【C++】类型转换 ④ ( 子类 和 父类 之间的类型转换 - 动态类型转换 dynamic_cast )
文章目录 一、子类 和 父类 之间的类型转换 - 动态类型转换 dynamic_cast1、构造父类和子类2、子类 和 父类 之间的类型转换 - 隐式类型转换3、子类 和 父类 之间的类型转换 - 静态类型转换 static_cast4、子类 和 父类 之间的类型转换 - 重新解释类型转换 reinterpret_cast5、…...

在CentOS 7.9上搭建高性能的FastDFS+Nginx文件服务器集群并实现外部远程访问
文章目录 引言第一部分:FastDFS介绍与安装1.1 FastDFS简介1.2 FastDFS安装1.2.1 安装Tracker Server1.2.2 安装Storage Server 1.3 FastDFS配置1.3.1 配置Tracker Server1.3.2 配置Storage Server1.3.3 启动FastDFS服务 第二部分:Nginx配置2.1 Nginx安装…...
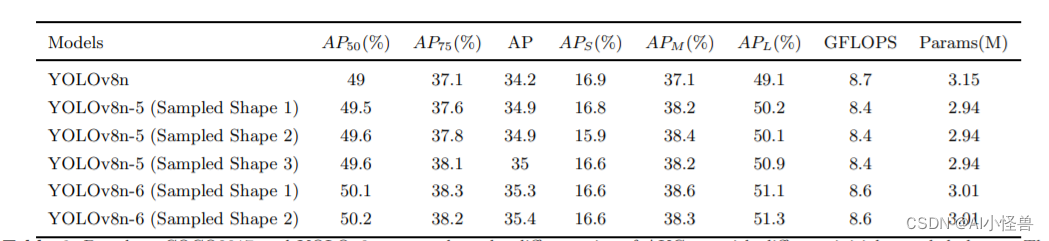
YOLOv8独家原创改进: AKConv(可改变核卷积),即插即用的卷积,效果秒杀DSConv | 2023年11月最新发表
💡💡💡本文全网首发独家改进:可改变核卷积(AKConv),赋予卷积核任意数量的参数和任意采样形状,为网络开销和性能之间的权衡提供更丰富的选择,解决具有固定样本形状和正方形的卷积核不能很好地适应不断变化的目标的问题点,效果秒殺DSConv 1)AKConv替代标准卷积进行…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
