代码随想录算法训练营 ---第四十五天
前言:
昨天的题做过之后,今天的题基本上都很简单,但是要注重一下细节。
第一题:

简介:
动态规划五部曲:
1.确定dp数组的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法
2.确定dp公式
i:可以看作本次的物品值
j:可以看作背包容量
dp[j] +=dp[j-i];
3.确定如何初始化dp数组
dp[0] = 1;
4.确定如何遍历数组
先遍历背包,再遍历物品(因为我们先迈一步再迈两步 还是 先迈两步再迈一步 是有区别的)
for(int j=0;j<=n;j++){for(int i=1;i<=m;i++){if(j-i>=0)dp[j] +=dp[j-i];}}5.打印数组,看是否正确
代码实现:
#include <iostream>
#include <vector>
using namespace std;int palou(int m,int n){vector<int> dp(n+1,0);dp[0] = 1;for(int j=0;j<=n;j++){for(int i=1;i<=m;i++){if(j-i>=0)dp[j] +=dp[j-i];}}return dp.back();
}int main(){int m,n;cin>>n>>m;cout<<palou(m,n);return 0;
}第二题:

简介:
我认为本题的重点在于如何初始化dp数组,自己做时在那里吃了亏。
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2.确定递推公式 递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); 如果放入就加一个金币,不放入就不加。
3.dp数组如何初始化 首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;然后考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。所以下标非0的元素都是应该是最大值。
代码如下:
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
4.确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。所以本题并不强调集合是组合还是排列。如果求组合数就是外层for循环遍历物品,内层for遍历背包。如果求排列数就是外层for遍历背包,内层for循环遍历物品。所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!

5.举例推导dp数组
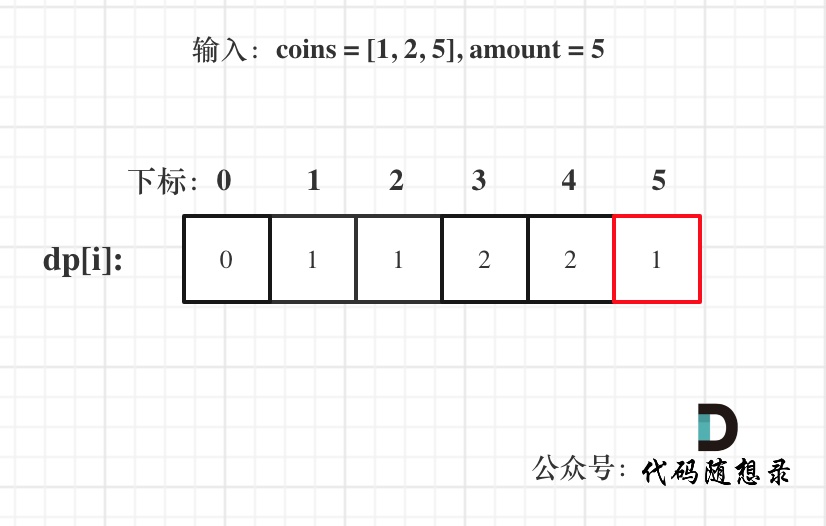
dp[amount]为最终结果。
代码实现:
//dp[j]表示组成j 所需最少硬币个数int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,INT_MAX);dp[0]=0;for(int i=0;i<coins.size();i++){for(int j=coins[i];j<=amount;j++){if (dp[j - coins[i]] != INT_MAX)dp[j] =min(dp[j],dp[j-coins[i]]+1); }}if(dp.back()==INT_MAX)return -1;elsereturn dp.back();}第三题:

简介:
本题和上一题十分相似,只不过我们在遍历时要注意完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?这样本题是不是就很清晰了。
代码实现:
先遍历背包,再遍历物品
int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}}return dp[n];}先遍历物品,再遍历背包
int numSquares(int n) {if(n<4)return n;vector<int> dp(n+1,INT_MAX);dp[0] = 0;for(int i=1;i*i<=n;i++){for(int j=i*i;j<=n;j++){dp[j] =min(dp[j],dp[j-i*i]+1);}}return dp.back();}总结:
今天使用感觉更加得心应手了,还需努力!
相关文章:

代码随想录算法训练营 ---第四十五天
前言: 昨天的题做过之后,今天的题基本上都很简单,但是要注重一下细节。 第一题: 简介: 动态规划五部曲: 1.确定dp数组的含义 dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法 2.确定dp…...
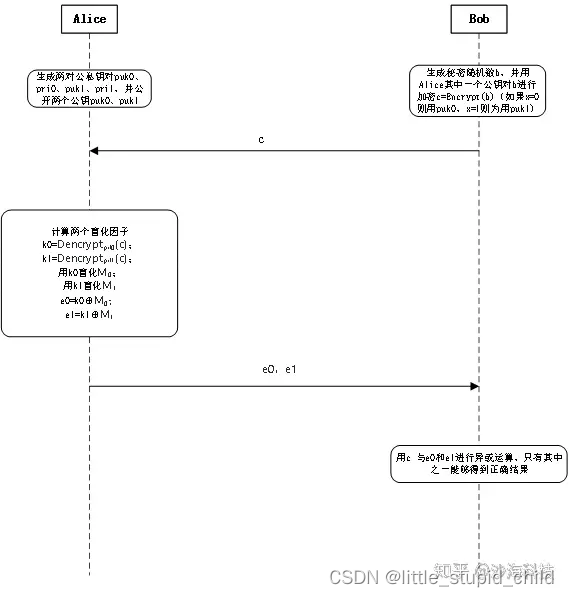
【密码学】【多方安全计算】不经意传输(Oblivious Transfer,OT)
文章目录 不经意传输(oblivious transfer)定义不经意传输的实例(1 out 2,二选一不经意传输)基于RSA的1 out 2 不经意传输疑问 不经意传输(oblivious transfer)定义 不经意传输(obli…...

STL常用算法-C++
概述: 算法主要是由头文件 <algorithm> <functional> <numeric> 组成。<algorithm> 是所有 STL 头文件中最大的一个,范围涉及是比较、交换、查找、遍历操作、复制、修改等等。<functional> 定义了一些模板类,…...

一、Lua基础
文章目录 一、Lua是什么二、Lua特性(一)轻量级(二)可扩展(三)其它特性 三、Lua安装四、Lua应用 看到评论说,C让我见识了语言的严谨与缜密,lua让我见识到了语言的精巧与创新ÿ…...

vue3 webSocket 封装及使用
vue3 webSocket 封装及使用 封装 import { ref, onUnmounted } from vue; interface SocketOptions {heartbeatInterval?: number;reconnectInterval?: number;maxReconnectAttempts?: number; }class Socket {url: string;ws: WebSocket | null null;opts: SocketOption…...
)
记录vscode常用插件集合(extensions)
名称用处Chinese (Simplified) (简体中文) Language Pack for Visual Studio Code适用于 VS Code 的中文(简体)语言包Dev ContainersVisual Studio代码开发容器ES7 React/Redux/GraphQL/React-Native snippetsES7 React/Redux/GraphQL/Rect Native代码段…...

正则表达式详解
一、正则表达式概述 正则表达式是一组由字母和符号组成的特殊文本,它可以用来从文本中找出满足你想要的格式的句子。通俗的讲就是按照某种规则去匹配符合条件的字符串 一个正则表达式是一种从左到右匹配主体字符串的模式。 “Regular expression”这个词比较拗口&a…...

【限时免费】20天拿下华为OD笔试之【双指针】2023Q1A-两数之和绝对值最小【欧弟算法】全网注释最详细分类最全的华为OD真题题解
文章目录 题目描述与示例题目描述输入输出示例一输入输出说明 解题思路代码解法一pythonjavacpp 解法二pythonjavacpp 时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 题目描述与示例 题目描述 给定一个整数数组nums,请你在该数组中找出两个数,…...

expect脚本在自动化部署中的具体应用案例
#expect脚本在自动化部署中的具体应用 expect脚本是一个非常好的交互式应用脚本,在自动化部署中,可以使用这个脚本来实现全自动的自动化部署。下面是一些具体的应用案例。 场景一:自动安装mysql 可以使用expect脚本来实现mysql自动安装&…...
【Java+SQL Server】前后端连接小白教程
目录 📋 流程总览 ⛳️【SQL Server】数据库操作 1. 新建数据库text 2. 新建表 3. 编辑表 ⛳️【IntelliJ IDEA】操作 1. 导入jar包 2. 运行显示错误 📋 流程总览 ⛳️【SQL Server】数据库操作 打开SQL Server数据库-->sa登录-->新建数据库…...
Xilinx Zynq-7000系列FPGA多路视频处理:图像缩放+视频拼接显示,提供工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐FPGA图像处理方案FPGA图像缩放方案FPGA视频拼接叠加融合方案推荐 3、设计思路详解HLS 图像缩放介绍Video Mixer介绍 4、vivado工程介绍PL 端 FPGA 逻辑设计PS 端 SDK 软件设计 5、工程移植说明vivado版本不一致处理FPGA型号不一致处理其他…...

Web语言基础课程期末代做
《Web语言基础》课程期末考核要求综合运用课程所学知识,使用VS和SQL及相关开发工具,结合DIVCSS等前端设计技术,完成一个具备新闻发布和考试功能的动态系统,要求包括但不限于:用户注册、登录功能、新闻展示功能、后台数…...

Scanner常用知识点
在Java中,Scanner类是用于读取用户输入的工具类,可以从多种输入源读取数据,如标准输入流、文件或字符串。以下是一些Scanner类的常用知识点: Scanner的初始化:在使用Scanner类之前,需要先将其导入到你的Ja…...
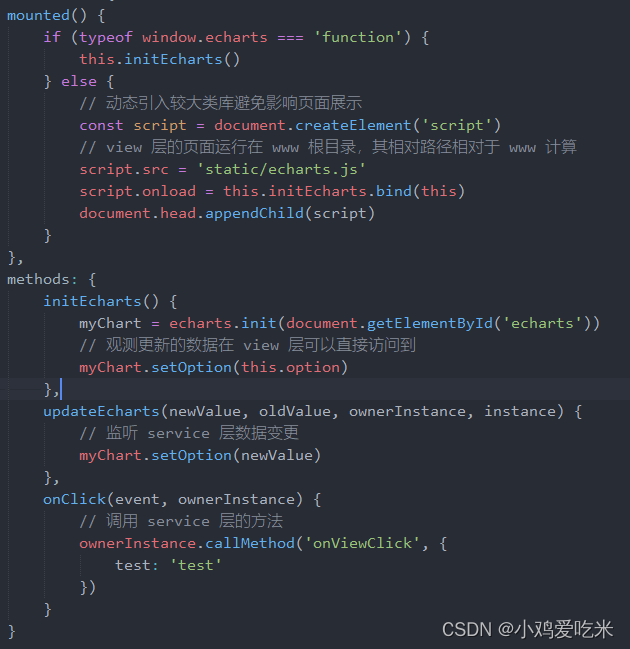
uniapp页面使用多个echarts出现数据渲染错乱问题解决
首先,uniapp当中使用echarts是在通过使用renderjs的script模板的前提下实现的,在官方提供的案例当中,核心代码是这一部分: 但如果将其封装为组件,并在一个页面当中引用多次来生成多个charts图标,那么这个时…...

PHP连接数据库 错误抑制 三元运算符 学习资料
PHP连接数据库 PHP可以通过不同的扩展和库来连接各种类型的数据库。下面是一个使用MySQL数据库的连接示例: <?php $servername "localhost"; $username "your_username"; $password "your_password"; $dbname "your_d…...
5G智慧工地整体解决方案:文件全文115页,附下载
关键词:5G智慧工地,智慧工地建设方案,智慧工地管理平台系统,智慧工地建设调研报告,智慧工地云平台建设 一、5G智慧工地建设背景 5G智慧工地是利用5G技术、物联网、大数据、云计算、AI等信息技术,围绕“人…...

数据结构 / 内存的动态申请和释放
1.内存的动态申请 malloc malloc 的头文件: #include <stdlib.h>格式: void *malloc(size_t size);参数: size_t size: 申请堆区内存大小, 单位是字节;size_t: 是数据类型, 是 unsigned long的宏定义的别名;返回值: void *: 通用类型指针,使用时需要强转为具…...

Android手电筒、闪光灯、torch、flash
1. 仅开启手电筒 单纯的开启手电筒我们可以使用CameraManager的.setTorchMode()方法。 cameraCharacteristics.get(CameraCharacteristics.FLASH_INFO_AVAILABLE)获取该相机特征是否可获取闪光灯。 CameraManager cameraManager (CameraManager) getSystemService(CAMERA_SE…...

C语言--每日选择题--Day26
第一题 1.在C语言中,表示一次性地给数组a的10元素赋值() int a[10];scanf("%d",a); A:正确 B:错误 答案及解析 B 我们知道单独的数组名就是首元素地址,但是也有…...

[ACTF2020 新生赛]BackupFile
打开题目就一句话:尝试找到源文件 和上一题一样,用dirsearch扫描网站找到了一下内容 flag.php,0B,虚假flag 瞅一眼index.php.bak是啥 下载了一个文件,把bak后缀删掉,打开了index.php源码 is_numeric()&am…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
