关于Could not build wheels for opencv-python-headless, which is...报错的解决方案
在通过最新版pip在线安装package：opencv-python-headless的时候，会产生报错信息，主要为
ERROR: Failed building wheel for opencv-python-headless
ERROR: Could not build wheels for opencv-python-headless, which is required to install pyproject.toml-based projects
如图：
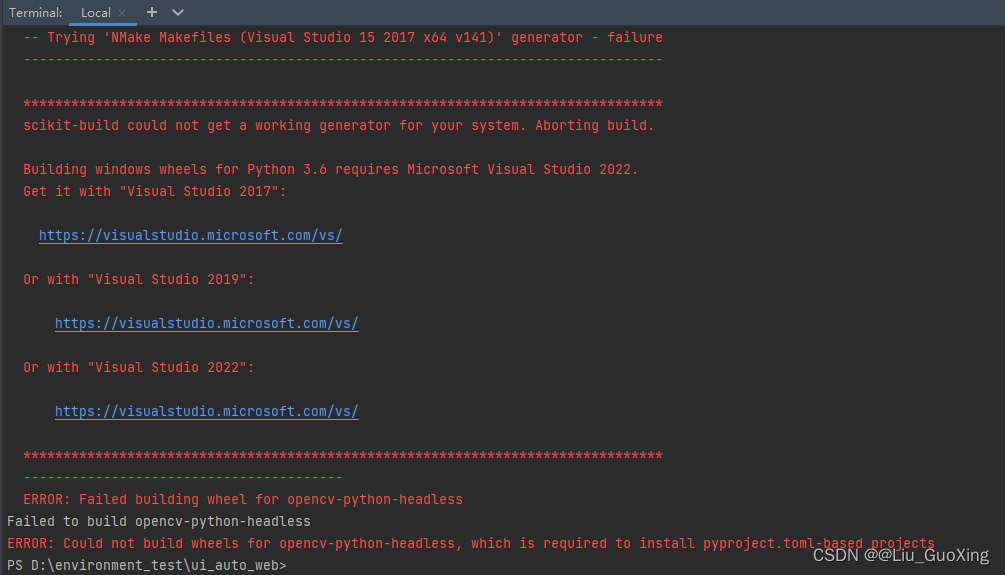
解决方案一：在线加载（简单快捷，成功率较低）
1、进入pycharm或dos页面
2、输入如下命令后回车等待自动安装：
pip3 install opencv-python-headless解决方案二：离线加载（步骤偏多，成功率很高）
1、进入官网下载opencv-python-headless
点击此处直接进入官网
https://pypi.org/project/opencv-python-headless/3.4.18.65/#files2、选择对应自己电脑python版本的文件，如我的电脑用的是python3.6，那就需要选择带有cp36字样的文件，amd64表示支持的是64位操作系统（目前用32位的电脑已经不多见了）
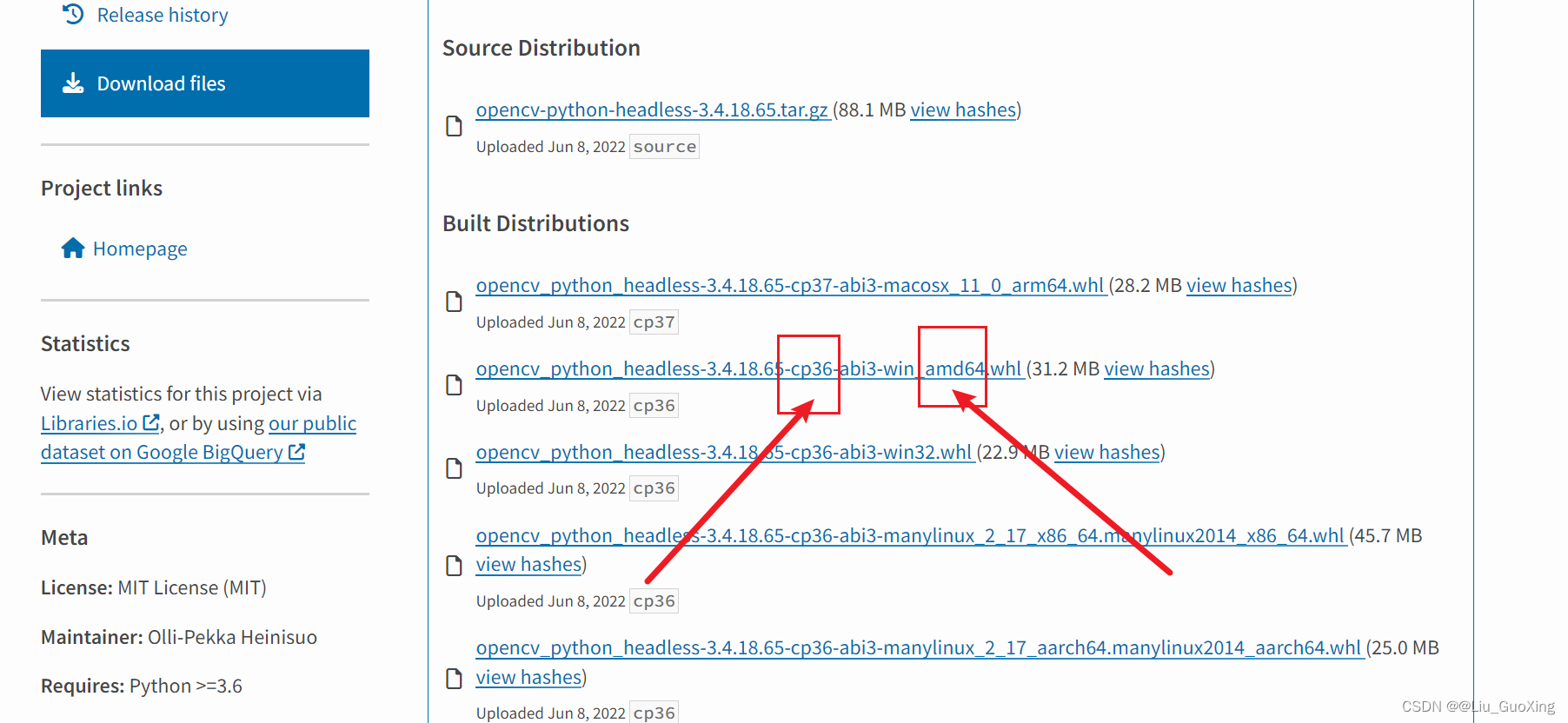
3、点击文件名后开始下载，下载后在桌面上或者电脑中的任意位置新建一个纯英文命名的文件夹，名称随意，比如aaa，将刚刚下载的文件粘贴到纯英文命名的文件夹中
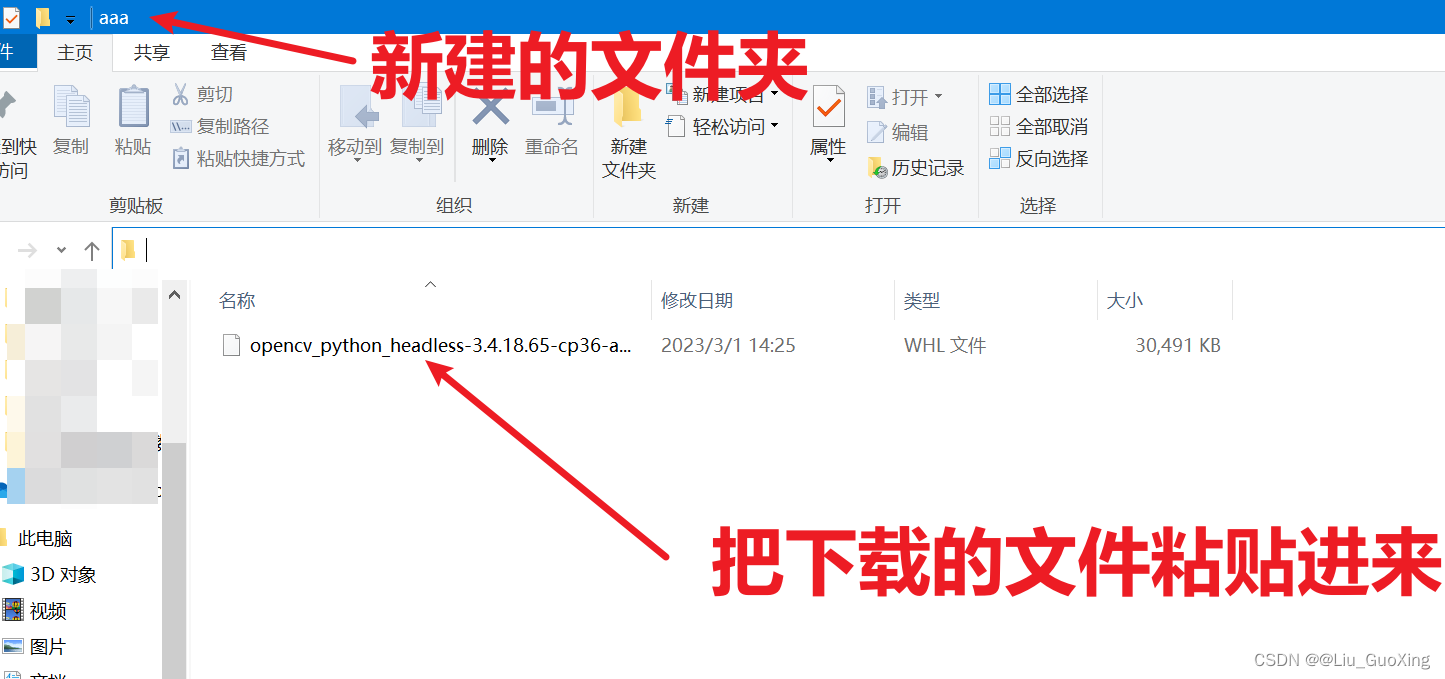
4、点击文件夹中的地址栏，删掉原有地址，输入cmd后回车
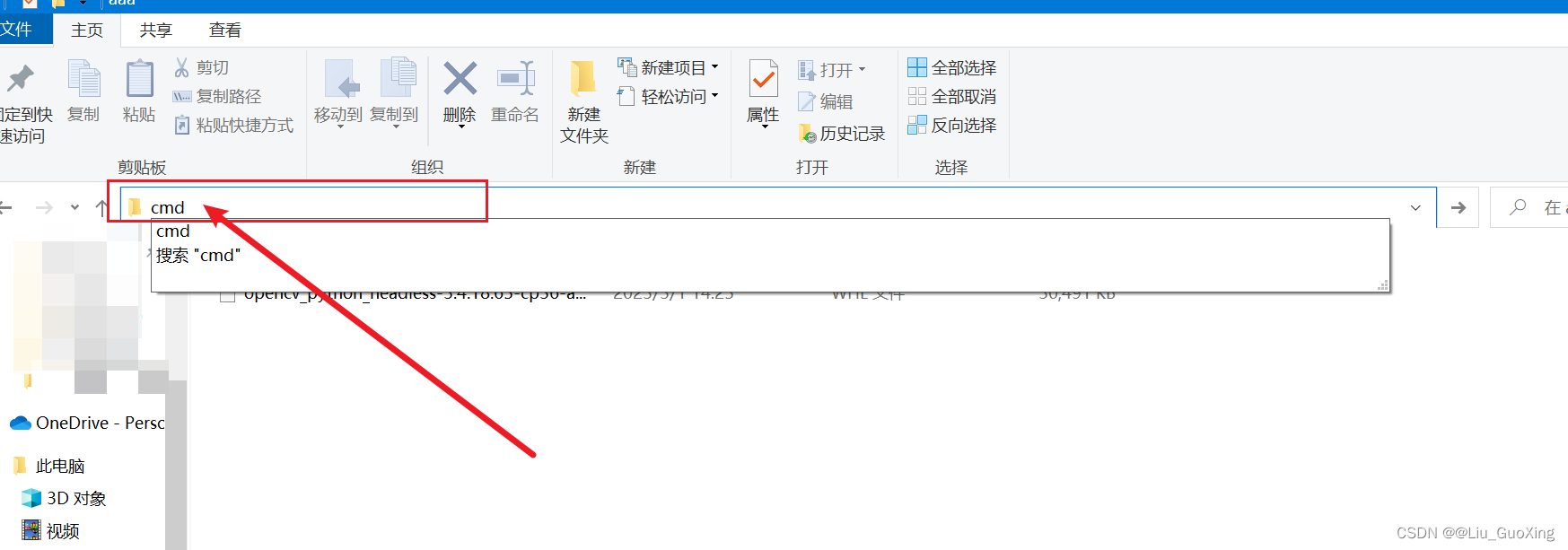
5、 输入pip3 install 文件名（文件名只需要输入开头几个字母按一下tab键就可以自动补齐了）
pip3 install opencv_python_headless-xxxxxxxxxx.whl
#（例子）例子如图：
6、输入完命令后按回车等待其出现success字样即可，此方法成功率非常高
❤关注我，不迷路❤
******我的本文相关专栏******
软件测试 & 开发（单击此处进入）
******我的其它作品专栏******
PC常见故障汇总专栏（点击进入）
EXCEL综合场景应用详解（点击此处进入）
全国计算机等级考试-二级python基础（点击此处进入）
相关文章：
关于Could not build wheels for opencv-python-headless, which is...报错的解决方案
在通过最新版pip在线安装package：opencv-python-headless的时候，会产生报错信息，主要为 ERROR: Failed building wheel for opencv-python-headless ERROR: Could not build wheels for opencv-python-headless, which is required to insta…...
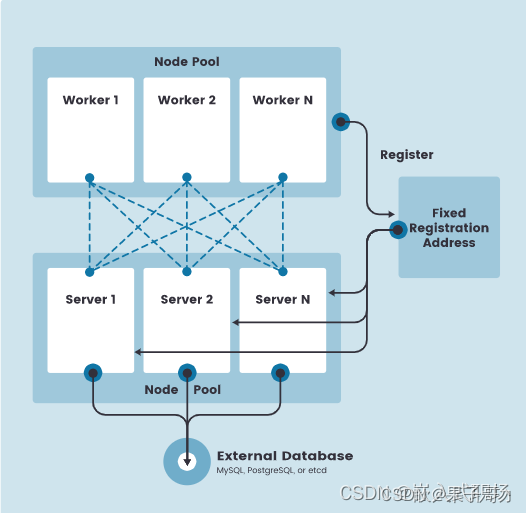
【K3s】第1篇 K3s入门级介绍及架构详解
1、什么是 K3s? K3s 是一个轻量级的 Kubernetes 发行版，它针对边缘计算、物联网等场景进行了高度优化。K3s 有以下增强功能： 打包为单个二进制文件。使用基于 sqlite3 的轻量级存储后端作为默认存储机制。同时支持使用 etcd3、MySQL 和 PostgreSQL 作…...
Java学习--反射
1. 反射 1.1 反射的概述： **专业的解释（了解一下）：**是在运行状态中，对于任意一个类，都能够知道这个类的所有属性和方法；对于任意一个对象，都能够调用它的任意属性和方法ÿ…...
应用和迭代（名词解释）
应用和迭代是什么意思 应用： ● 一个完整的前端应用，一般用应用脚手架创建，包含路由，页面，状态等 ● 一个应用对应一个代码仓库 ● 应用的分组（业务中心，数据中台等）只用于逻辑分类&…...
HTMLCollection 和 NodeList 区别
Node 和 Element DOM 是一棵树，所有节点都是 NodeNode 是 Element 的基类Element 是其他 HTML 元素的基类，如 HTMLDivElement HTMLCollection 和 NodeList HTMLCollection 是 Element 的集合NodeList 是 Node 的集合 <body><p id"p1&qu…...
fork()出来一个进程，这个进程的父进程是从哪来的？
基本概念fork() creates a new process by duplicating the calling process. The new process is referred to as the child process. The calling process is referred to as the parent process.fork()是一个系统调用，不是一个函数。详细信息可以，man…...
结构体内存对齐
结构体相信大家已经了解过了，现在我们深入讨论一个问题，计算结构体的大小 也是很热门的一个考点：结构体内存对齐 先看看下面结构体的大小 typedef struct Test {char a;char b;char c; }Test; 很容易看出答案为3，结构体的大小位…...
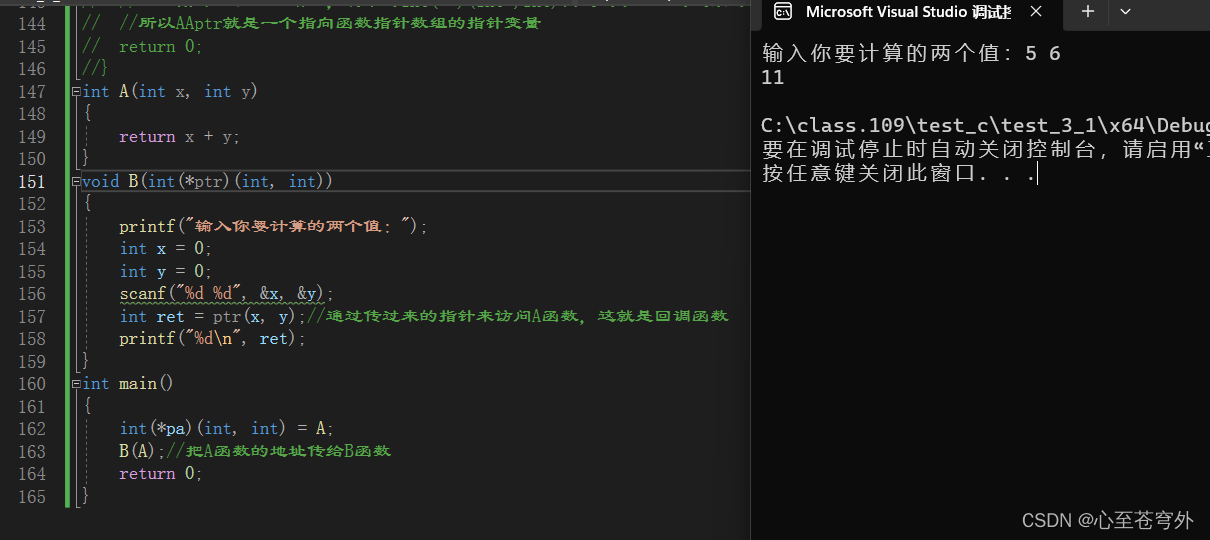
【C语言进阶】指针进阶
今日所做之事勿候明天，自我所做之事勿候他人。 --歌德 目录 指针进阶(更深层次的理解): 一.字符指针 二.指针数组 三.数组指针 1.数组指针的定义: 2.&数组名和数组名: 3.数组指针的使用: 四.数组参数，指针参数 1.一维数组传参:…...
java：Class的isPrimitive方法使用
java：Class的isPrimitive方法使用 1 前言 java中Class类的isPrimitive方法，用于检查类型是否为基本类型。java虚拟机创建了int、byte、short、long、float、double、boolean、char这8种基础信息，以及void，一共9种。为这9种类型时…...
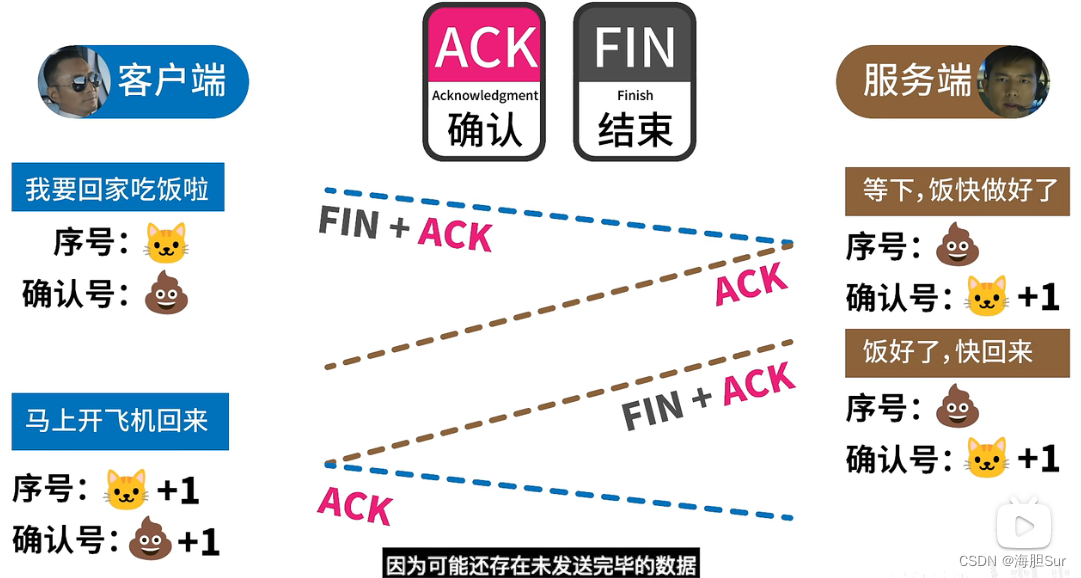
TCP 握手过程 三次 四次
蛋老师视频 SYN 同步 ACK 确认 FIN 结束 核心机制是确定哪些请求或响应需要丢弃 SYN、ACK、FIN 通过 1/0 设置开启/关闭 开启SYN后，报文中会随机生成 Sequence序号 用于校验 （应用可能发起多个会话，可以区分） 服务器的同步序…...
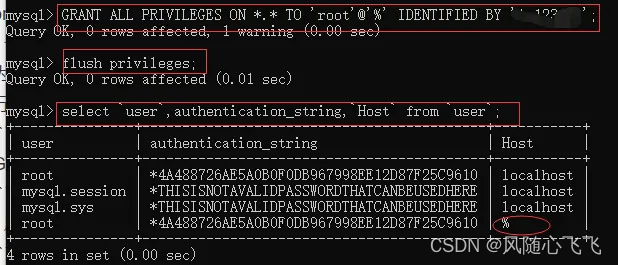
windows 下 安裝mysql 5.7.41 （64位） 超简单方式
文章目录1. 安装包下载2.安装步骤3. 服务卸载方式4. 配上 my.ini 常用配置1. 安装包下载 注意，截至2023年2月23日，MySQL所有版本不提供ARM芯片架构的Windows版本(8.0.12开始支持Red Hat系统的ARM版本)，所以ARM架构的Windows无法安装MySQL&am…...
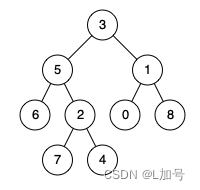
二叉树——二叉树的最近公共祖先
二叉树的最近公共祖先 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一…...
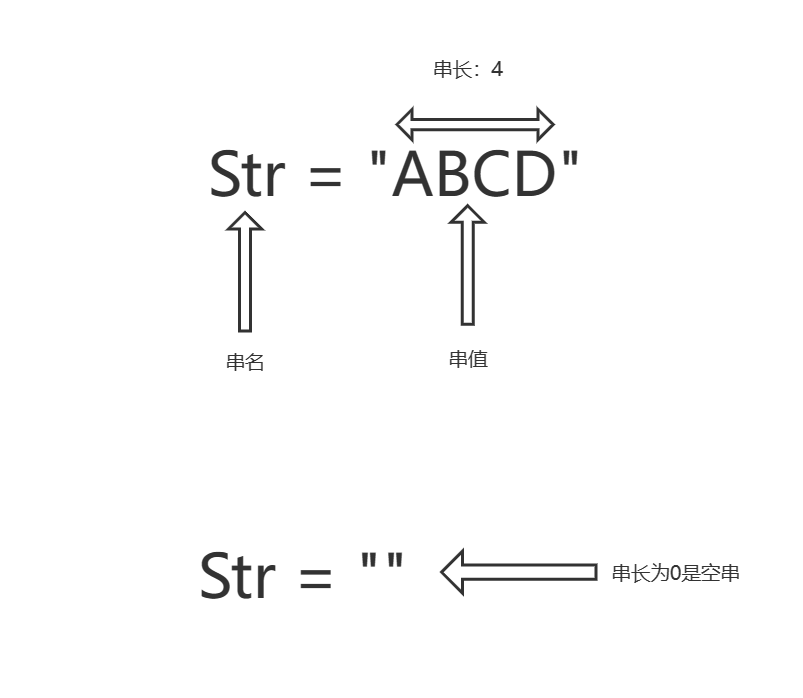
数据结构与算法基础-学习-14-线性表之串
一、串的定义由0-n个字符组成的有限序列。（n>0）二、串的相关术语1、子串串中任意个连续字符组成的子序列成为该串的子串。2、主串包含子串的串成为主串。3、字符位置字符在序列中的序号为该字符在串中的位置。4、子串位置子串第一个字符在主串中的位置…...
Mac 快捷键
目录 命令行快捷键 命令行快捷键 control d 命令行中代表发送EOF终止输入 control u 删除光标之前到行首的字符 control k 删除光标之前到行尾的字符(比较常用) control a 移动光标到行首(常用) control e 移动光标到行尾 control l 清屏，相当于clear命令 con…...
【微服务】-微服务环境搭建
目录 2.1 技术选型 2.2 模块设计 2.3 微服务调用 2.4 创建⽗⼯程 2.5 创建商品微服务 2.6 创建订单微服务 2.1 技术选型 持久层: SpingData Jpa 数据库: MySQL5.7 其他: SpringCloud Alibaba 技术栈 2.2 模块设计 --- shop-parent ⽗⼯程 --- shop-product-api 商品微服…...
IGKBoard（imx6ull）-ADC编程MQ-2烟雾传感器采样
文章目录1- ADC介绍2- MQ-2烟雾传感器介绍（1）工作原理（2）MQ-2应用电路3- MQ-2烟雾传感器硬件连接4- ADC驱动配置5- 编程查看当前浓度1- ADC介绍 ADC是Analog-to-Digital Converter的缩写，指模数转换器。真实世界的模拟…...
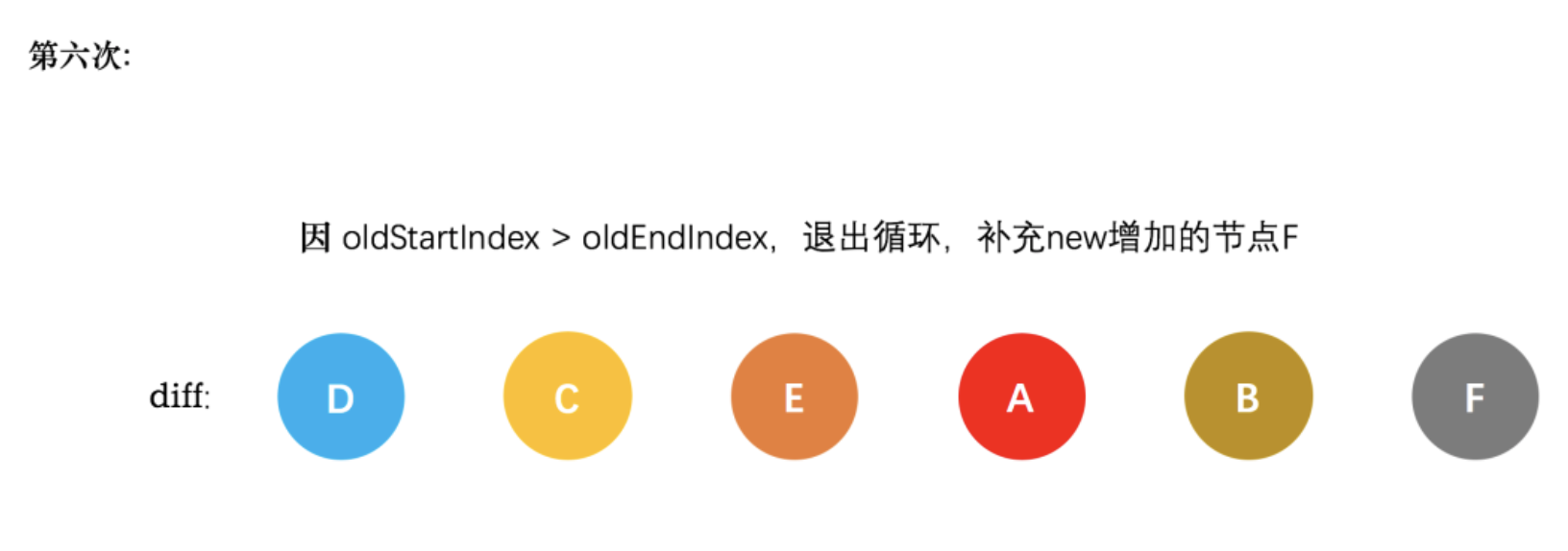
前端二面vue面试题总结
什么是 mixin ？ Mixin 使我们能够为 Vue 组件编写可插拔和可重用的功能。如果希望在多个组件之间重用一组组件选项，例如生命周期 hook、 方法等，则可以将其编写为 mixin，并在组件中简单的引用它。然后将 mixin 的内容合并到组件中…...
时间API在更新，传奇已经谢幕，但技术永远不死
（Bill Joy(左一)，Vinod Khosla(左二)，Andy Bechtolsheim(右二)，Scott McNealy(右一) ） CSDN 博文征集活动（和日期相关的代码和bug）：点击这里 各位 “big guys”，这篇博文…...
SQL调优指南笔记22：Gathering Diagnostic Data with SQL Test Case Builder
本文为SQL Tuning Guide 第21章“Gathering Diagnostic Data with SQL Test Case Builder”的笔记。 SQL Test Case Builder 是一种工具，可自动收集在不同数据库实例中重现问题所需的信息。 SQL 测试用例是一组信息，使开发人员能够为遇到性能问题的特定…...
从0开始学python -43
Python3 正则表达式 正则表达式是一个特殊的字符序列，它能帮助你方便的检查一个字符串是否与某种模式匹配。 Python 自1.5版本起增加了re 模块，它提供 Perl 风格的正则表达式模式。 re 模块使 Python 语言拥有全部的正则表达式功能。 compile 函数根…...
DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
Java如何权衡是使用无序的数组还是有序的数组
在 Java 中，选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南： ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
条件运算符
C中的三目运算符（也称条件运算符，英文：ternary operator）是一种简洁的条件选择语句，语法如下： 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true，则整个表达式的结果为“表达式1”…...
JVM垃圾回收机制全解析
Java虚拟机（JVM）中的垃圾收集器（Garbage Collector，简称GC）是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象，从而释放内存空间，避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...
多模态商品数据接口：融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 （一）多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如，当用户上传一张“蓝色连衣裙”的图片时，接口可自动提取图像中的颜色（RGB值&…...
NLP学习路线图（二十三）：长短期记忆网络（LSTM）
在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN） 曾被视为…...
爬虫基础学习day2
# 爬虫设计领域 工商：企查查、天眼查短视频：抖音、快手、西瓜 ---> 飞瓜电商：京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空：抓取所有航空公司价格 ---> 去哪儿自媒体：采集自媒体数据进…...
docker 部署发现spring.profiles.active 问题
报错： org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持，SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库（解决显示问题） sudo apt install fonts-wqy…...
tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效，稳定，易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...