当前位置： 首页 > news >正文

计算4人队形的最可能分布

news 2026/2/8 11:15:50

2

2

2

1

2

2

2

2

2

1

2

2

2

2

2

1

2

2

3

3

3

x

3

3

2

2

2

1

2

2

2

2

2

1

2

2

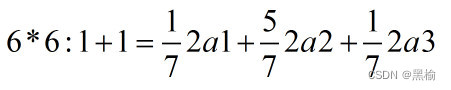
在6*6的平面上2个点随机分布，有3种分布方式，2a1，2a2，2a3，占比为1：5：1.

3

3

3

2

3

3

3

3

3

2

3

3

1

1

1

x

1

1

1

1

1

x

1

1

3

3

3

2

3

3

3

3

3

2

3

3

在2a1上增加一个点，有3种分布方式，3a1，3a2，3a3，占比是5：2：10

5

5

3

3

5

5

5

5

3

3

5

5

4

4

x

1

4

4

4

4

1

x

4

4

5

5

3

3

5

5

5

5

3

3

5

5

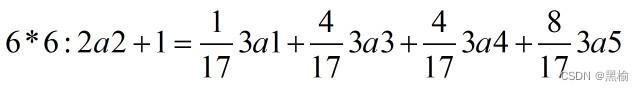
4

4

1

1

4

4

4

4

1

1

4

4

4

4

1

1

4

4

6

6

x

x

6

6

4

4

1

1

4

4

4

4

1

1

4

4

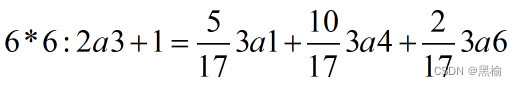
同样的办法得到2a2+1和2a3+1.

把2a1+1，2a2+1，2a3+1代入1+1的表达式得到

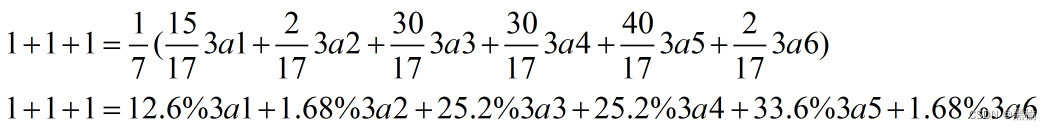
在此基础上计算3a1+1

2

2

2

1

3

2

2

2

2

1

3

2

2

2

2

1

3

2

4

4

4

1

1

4

14

14

14

12

1

14

2

2

2

1

3

2

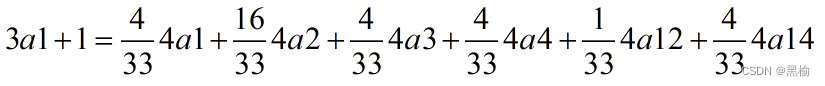
3a1+1把空间分成6部分，4a1，4a2，4a3，4a4，4a12，4a14，占比为4：16：4：4：1：4.所以如果在6*6的空间里已经有3个人排成3a1的结构，此时再来一个人，这个队伍最有可能变成4a2.

用同样的办法计算3a2+1，3a3+1，3a4+1，3a5+1，3a6+1

3a2+1

5

5

5

6

5

5

5

5

5

6

5

5

5

5

5

6

5

5

3

3

3

1

3

3

3

3

3

1

3

3

3

3

3

1

3

3

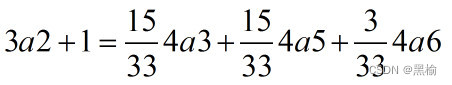
3a3+1

7

7

7

8

5

7

7

7

7

8

5

7

7

7

7

8

5

7

2

2

2

1

1

2

2

2

2

1

1

2

11

11

11

1

3

11

3a4+1

9

9

9

2

2

11

9

9

9

2

2

11

9

9

9

2

2

11

15

15

15

14

14

1

10

10

10

1

1

4

9

9

9

2

2

11

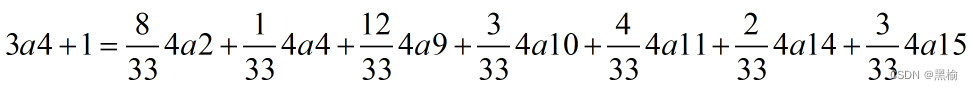
3a5+1

13

13

13

7

7

7

13

13

13

7

7

7

13

13

13

7

7

7

9

9

9

1

2

2

9

9

9

2

1

2

9

9

9

2

2

1

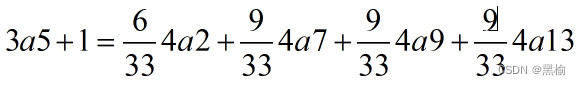
10

10

10

4

4

4

10

10

10

4

4

4

10

10

10

4

4

4

16

16

16

1

1

1

10

10

10

4

4

4

10

10

10

4

4

4

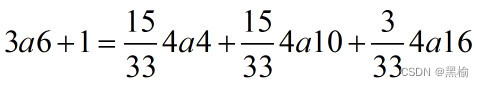
所以计算4人队形的所有组合就是计算1+1+1+1，因此把3a1+1，3a2+1，…，3a6+1代入

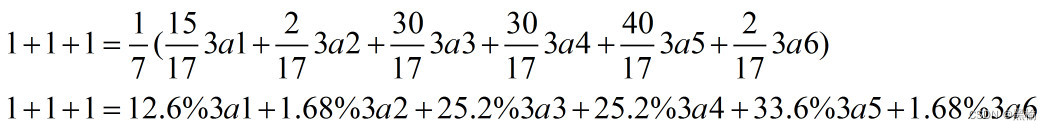
得到

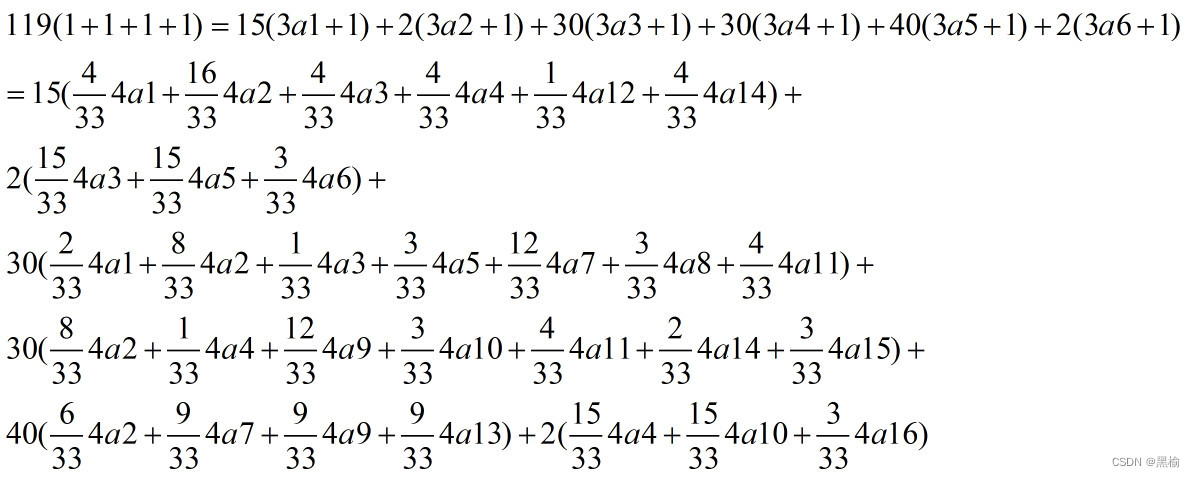
化简

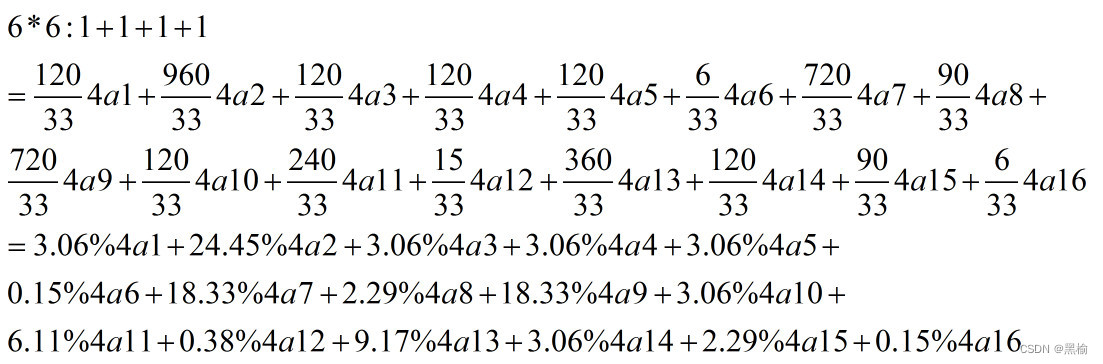
4个点16个结构的占比

1

2

3

4

5

6

7

8

0.0306

0.2445

0.0306

0.0306

0.0306

0.0015

0.1833

0.0229

9

10

11

12

13

14

15

16

0.1833

0.0306

0.0611

0.0038

0.0917

0.0306

0.0229

0.0015

所以在6*6的平面上4个人的队形最大概率为4a2，占比为24.45%其次是4a7和4a9占比都是18.33%，这3个分布就占总分布的61%。

2

-

-

-

-

-

1

24.45%

2

1

1

-

1

1

-

2

-

-

1

-

1

-

2

-

1

-

-

-

-

2

-

-

-

2

7

-

-

1

-

1

-

18.33%

7

-

-

-

-

1

-

7

-

-

1

1

-

-

7

1

-

-

-

-

1

7

-

1

-

7

9

-

-

1

-

-

-

1

-

18.33%

9

-

-

-

-

1

1

-

-

9

-

-

-

-

-

-

-

1

9

1

1

-

-

9

-

-

-

1

9

而这3种分布看起来都可能很像人字形。

计算机验算，随机向6*6的区域内扔4个石子，扔了1000次，2000次

计算

1000

2000

1

0.0306

33

0.033

65

0.0325

2

0.2445

233

0.233

464

0.232

3

0.0306

40

0.04

82

0.041

4

0.0306

28

0.028

68

0.034

5

0.0306

39

0.039

82

0.041

6

0.0015

2

0.002

8

0.004

7

0.1833

208

0.208

413

0.2065

8

0.0229

34

0.034

71

0.0355

9

0.1833

150

0.15

310

0.155

10

0.0306

30

0.03

59

0.0295

11

0.0611

71

0.071

129

0.0645

12

0.0038

7

0.007

9

0.0045

13

0.0917

78

0.078

139

0.0695

14

0.0306

25

0.025

69

0.0345

15

0.0229

22

0.022

28

0.014

16

0.0015

0

0

4

0.002

和计算数据基本一致。

相关文章：

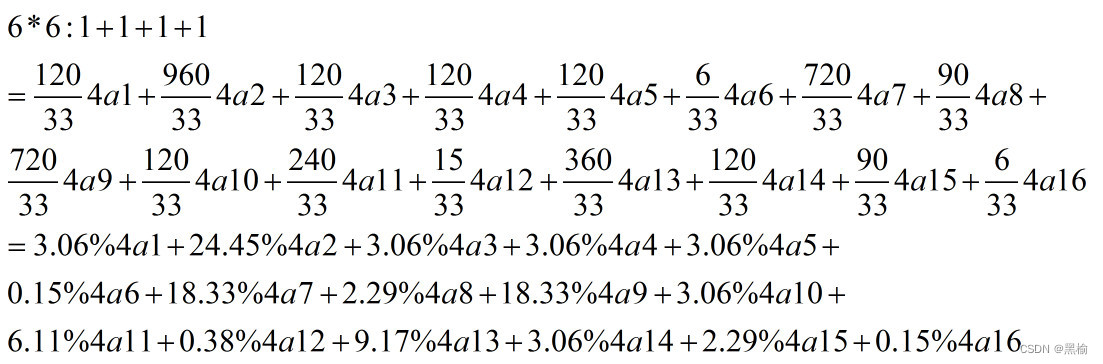
计算4人队形的最可能分布

2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 3 3 3 x 3 3 2 2 2 1 2 2 2 2 2 1 2 2 在6*6的平面上2个点随机分布，有3种分布方式，2a1，2a2，2a3，占比为1：5：1. 3 3 …...

编程日记 2023/11/28 23:03:37

如何解决 Java 中的 IllegalArgumentException 异常？

非法参数异常（IllegalArgumentException）的抛出是为了表明一个方法被传递了一个非法参数。该异常扩展了 RuntimeException 类，因此属于在 Java 虚拟机（JVM）运行期间可能抛出的异常。它是一种未检查异常，因此…...

编程日记 2023/11/28 23:02:36

Vue 双向数据绑定

之前通过v-bind来完成的数据绑定&#xff0c;属性值和表达式进行绑定&#xff0c;表达式的值发生变化了属性值也跟着发生变化。 单向数据绑定&#xff1a; <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>首页</titl…...

编程日记 2023/11/28 23:00:34

电脑开机过程中，程序的启动的顺序是怎么样的？

电脑的启动过程涉及多个步骤，程序按照特定的顺序启动。这个过程通常如下： 电源开启: 当你按下电源按钮时，电源供应器（PSU）开始向电脑的各个组件供电。 自检加电（POST）: 这是电脑启动过程的第一步。在这个阶段，基本输入输出系统（BIOS）或统一可扩展固件接口（UEFI）执行…...

编程日记 2023/11/28 22:59:33

JSON详细教程

&#x1f60a;JSON详细教程 &#x1f6a9;JSON简介☃️JSON语法规则&#x1f50a;JSON和JavaScript对象的区别 ☃️JSON数据类型字符串&#x1f50a;数字&#x1f50a;布尔值&#x1f50a;数组&#x1f50a;对象&#x1f50a;Null ☃️JSON对象&#x1f50a;访问JSON对象的值&a…...

编程日记 2023/11/28 22:58:31

DSP介绍及CCS

文章目录 CCS版本编译器CCS使用注意严禁中文 CCS的基本操作新建工程导入现有工程调整字体的大小工程界面恢复标签的使用 仿真盒小虫子进入在线Debug 仿真器芯片TMS320F28355基本介绍特性 DSP中特殊指令dsp指令中的EALLOW EDIS CCS TI官网 版本 CCS版本&#xff1a; CCS8.3.1…...

编程日记 2023/11/28 22:57:30

周期串（Periodic Strings）

做了我两个小时&#xff0c;我真的裂开 之前已经发过一次了&#xff0c;走在回宿舍的路上突然发现有些情况并不适用&#xff0c;赶紧删掉了 题目如下&#xff1a; 如果一个字符串可以由某个长度为k的字符串重复多次得到&#xff0c;则称该串以k为周期。例如&#xff1a;abca…...

编程日记 2023/11/28 22:56:29

C语言——猜凶手

题目&#xff1a; 日本某地发生了一件谋杀案&#xff0c;警察通过排查确定杀人凶手必为4个嫌疑犯的一个。 以下为4个嫌疑犯的供词: A说&#xff1a;不是我。 B说&#xff1a;是C。 C说&#xff1a;是D。 D说&#xff1a;C在胡说 已知3个人说了真话&#xff0c;1个人说的是假话。…...

编程日记 2023/11/28 22:55:28

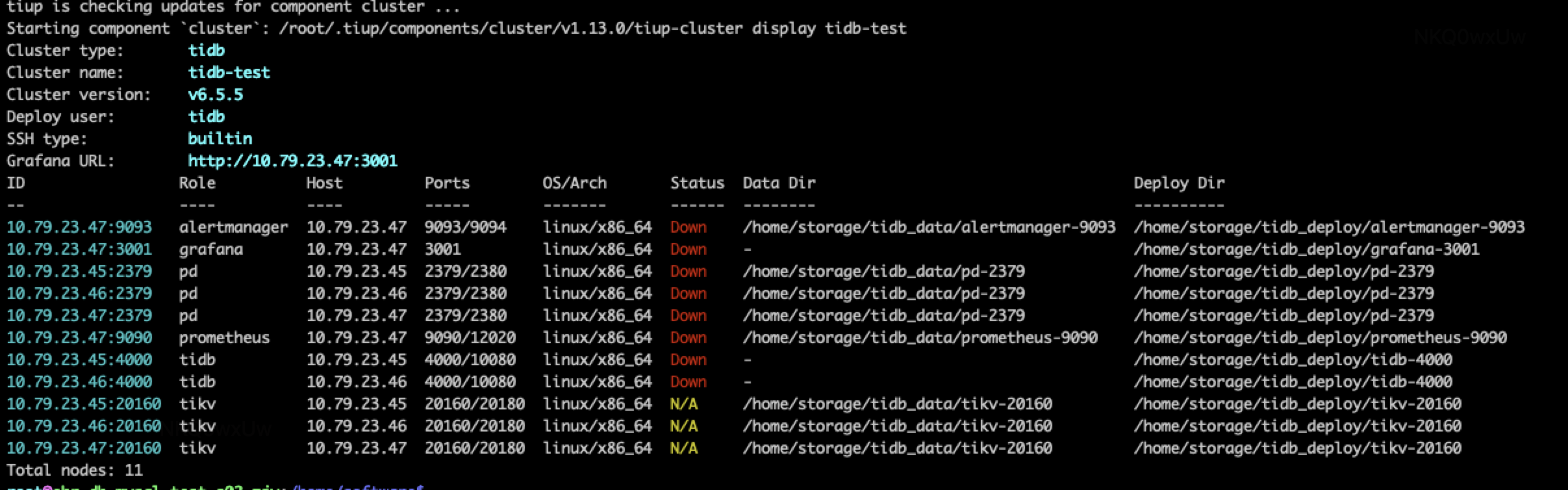
【TiDB】TiDB离线方式部署

目录 1 下载TiDB离线组件包 2 安装TiUP 3 合并离线包 4 TIDB 软件和硬件环境建议配置 5 TiDB环境与系统配置检查 6 生成集群初始化配置文件模板 7 执行部署命令 1 检查就能存在的潜在风险 2 手动修复风险 3 部署 TiDB 集群 8 查看TIUP管理的集群情况 9 检查部署的…...

编程日记 2023/11/28 22:54:27

android shape绘制半圆

<?xml version"1.0" encoding"utf-8"?><shape xmlns:android"http://schemas.android.com/apk/res/android"android:shape"rectangle"><sizeandroid:width"20dp"android:height"10dp" /><…...

编程日记 2023/11/28 22:53:25

【开源】基于Vue和SpringBoot的个人健康管理系统

项目编号&#xff1a; S 040 &#xff0c;文末获取源码。 \color{red}{项目编号&#xff1a;S040&#xff0c;文末获取源码。} 项目编号&#xff1a;S040&#xff0c;文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 健康档案模块2.2 体检档案模块2.3 健…...

编程日记 2023/11/28 22:52:24

qt QString字符串常用转换

QString字符串转换类型,常见的有: 1. const char*初始化QString.即const char*类型转QString字符串类型. QString str("肖战");qDebug() <<str; 2. QChar数组初始化QString.即QChar字符数组转QString字符串. QChar cHello[5] {H,e,l,l,o};QString strHell…...

编程日记 2023/11/28 22:50:22

JAVA sql 查询3

-- 1. 求各个月入职的的员工个数 select date_format(hiredate,%m),count(date_format(hiredate,%m)) from employees group by date_format(hiredate,%m) -- 2. 查询 50 号部门,60 号部门,70 号部门的各个部门的平均工资 SELECT department_id,avg(salary) FROM employees WH…...

编程日记 2023/11/28 22:49:21

PHP while 和 do-while 循环 学习资料

PHP while 和 do-while 循环 在 PHP 中&#xff0c;while 和 do-while 是两种常用的循环结构&#xff0c;用于重复执行一段代码&#xff0c;直到满足指定条件为止。以下是对这两种循环的介绍和示例&#xff1a; while 循环 while 循环用于在指定条件为真时重复执行代码块。循…...

编程日记 2023/11/28 22:47:19

OpenJudge NOI 1.8 16:矩阵剪刀石头布 c语言

描述 Bart的妹妹Lisa在一个二维矩阵上创造了新的文明。矩阵上每个位置被三种生命形式之一占据&#xff1a;石头&#xff0c;剪刀&#xff0c;布。每天&#xff0c;上下左右相邻的不同生命形式将会发生战斗。在战斗中&#xff0c;石头永远胜剪刀&#xff0c;剪刀永远胜布&#…...

编程日记 2023/11/28 22:46:18

mysql 性能参数调优详解

1 优化连接池 连接池运行机制 MySQL连接器中的连接池&#xff0c;用以提高数据库密集型应用程序的性能和可扩展性&#xff0c;默认启用。MySQL连接器负责管理连接池中的多个连接&#xff0c;自动创建、打开、关闭和破坏连接&#xff0c;多个连接的创建&#xff0c;可满足多客户…...

编程日记 2023/11/28 22:44:16

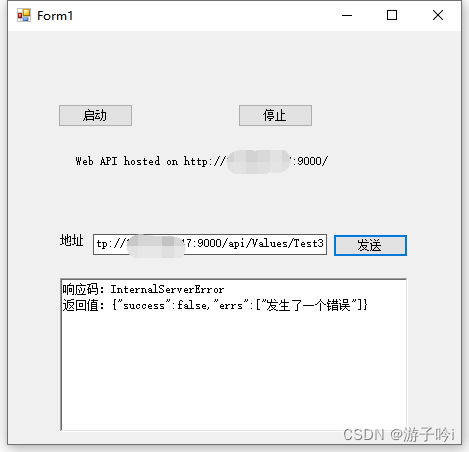
基于.net framework4.0框架下winform项目实现寄宿式web api

首先Nuget中下载包&#xff1a;Microsoft.AspNet.WebApi.SelfHost&#xff0c;如下&#xff1a; 注意版本哦&#xff0c;最高版本只能4.0.30506能用。 1.配置路由 public static class WebApiConfig{public static void Register(this HttpSelfHostConfiguration config){// …...

编程日记 2023/11/28 22:43:15

Vue中项目进行文件压缩与解压缩 （接口返回文件的url压缩包前端解析并展示出来，保存的时候在压缩后放到接口入参进行保存）

安装 npm install pako在Vue组件中引入pako&#xff1a; import pako from pako;接口返回的url是这个字段 tableSsjsonUrl 其实打开就是压缩包const source await tableFileUrl ({ id: this.$route.query.id}); if(source.code 0) {this.titleName source.data.tableNam…...

编程日记 2023/11/28 22:42:14

Linux shell编程学习笔记31：alias 和 unalias 操作 命令别名

目录 0 前言1 定义别名2 查看别名 2.1 查看所有别名2.2 查看某个别名 2.2.1 alias 别名2.2.2 alias | grep 别名字符串2.2.3 使用 CtrlAltE 组合键3 unalias&#xff1a;删除别名4 如何执行命令本身而非别名 4.1 方法1&#xff1a;使用 CtrlAltE 组合键 && unalias4…...

编程日记 2023/11/28 22:41:13

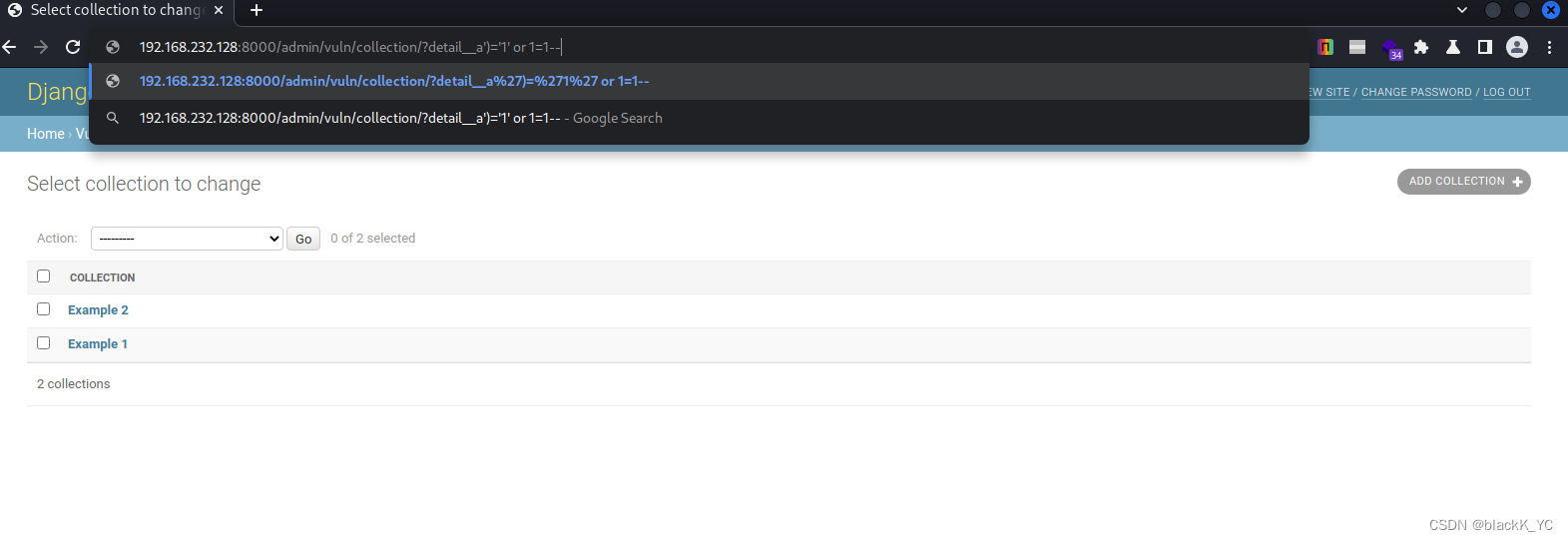
Django JSONField/HStoreField SQL注入漏洞（CVE-2019-14234）

漏洞描述 Django 于2019年8月1日 日发布了安全更新&#xff0c;修复了 JSONField 和 HStoreField 两个模型字段的 SQL 注入漏洞。 参考链接&#xff1a; Django security releases issued: 2.2.4, 2.1.11 and 1.11.23 | Weblog | DjangoDjango JSONField SQL注入漏洞&#x…...

编程日记 2023/11/28 22:40:12

Leetcode 3577. Count the Number of Computer Unlocking Permutations

Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接&#xff1a;3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯&#xff0c;要想要能够将所有的电脑解锁&#x…...

编程新知 2026/1/4 2:33:39

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户&#xff0c;但你不希望用 root 权限运行 ns-3&#xff08;这是对的&#xff0c;ns3 工具会拒绝 root&#xff09;&#xff0c;你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案&#xff1a;创建非 roo…...

编程新知 2025/9/11 11:00:29

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战

“&#x1f916;手搓TuyaAI语音指令 &#x1f60d;秒变表情包大师&#xff0c;让萌系Otto机器人&#x1f525;玩出智能新花样&#xff01;开整&#xff01;” &#x1f916; Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制&#xff08;TuyaAI…...

编程新知 2026/1/30 16:09:53

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/11/20 14:26:29

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2026/2/6 1:04:23

NXP S32K146 T-Box 携手 SD NAND（贴片式TF卡）：驱动汽车智能革新的黄金组合

在汽车智能化的汹涌浪潮中&#xff0c;车辆不再仅仅是传统的交通工具&#xff0c;而是逐步演变为高度智能的移动终端。这一转变的核心支撑&#xff0c;来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒&#xff08;T-Box&#xff09;方案&#xff1a;NXP S32K146 与…...

编程新知 2026/1/24 14:43:35

Python Einops库：深度学习中的张量操作革命

Einops&#xff08;爱因斯坦操作库&#xff09;就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库&#xff0c;用类似自然语言的表达式替代了晦涩的API调用&#xff0c;彻底改变了深度学习工程…...

编程新知 2025/10/16 12:04:52

淘宝扭蛋机小程序系统开发：打造互动性强的购物平台

淘宝扭蛋机小程序系统的开发&#xff0c;旨在打造一个互动性强的购物平台&#xff0c;让用户在购物的同时&#xff0c;能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机&#xff0c;实现旋转、抽拉等动作&#xff0c;增…...

编程新知 2026/1/31 7:11:11

QT开发技术【ffmpeg + QAudioOutput】音乐播放器

一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下&#xff0c;音视频内容犹如璀璨繁星&#xff0c;点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频&#xff0c;到在线课堂中知识渊博的专家授课&#xff0c;再到影视平台上扣人心弦的高清大片&#xff0c;音…...

编程新知 2026/2/4 5:32:18

如何让非 TCP/IP 协议驱动屏蔽 IPv4/IPv6 和 ARP 报文？

——从硬件过滤到协议栈隔离的完整指南 引言 在现代网络开发中，许多场景需要定制化网络协议（如工业控制、高性能计算），此时需确保驱动仅处理特定协议，避免被标准协议（如 IPv4/IPv6/ARP）干扰。本文基于 Linux 内核驱动的实现，探讨如何通过硬件过滤、驱动层拦截和协议栈…...

编程新知 2025/11/27 0:24:07