不同路径 II(力扣LeetCode)动态规划
不同路径 II
题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
- m == obstacleGrid.length
- n == obstacleGrid[i].length
- 1 <= m, n <= 100
- obstacleGrid[i][j] 为 0 或 1
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。 - 确定递推公式
递推公式和62.不同路径⼀样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这⾥需要注意⼀点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
在不同路径不同路径中我们给出如下的初始化:
vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
因为从(0, 0)的位置到(i, 0)的路径只有⼀条,所以dp[i][0]⼀定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是⾛不到的位置了,所以障碍之后的dp[i][0]应该还是
初始值0。
如图:
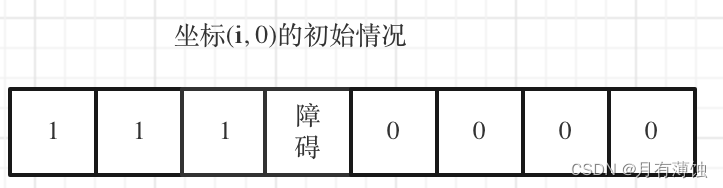
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
注意代码⾥for循环的终⽌条件,⼀旦遇到obstacleGrid[i][0] == 1的情况就停⽌dp[i][0]的赋值1的操作,dp[0][j]同理
4. 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,⼀定是从左到右⼀层⼀层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]⼀定是有数值。
代码如下:
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}
}
- 举例推导dp数组
拿示例1来举例如题:
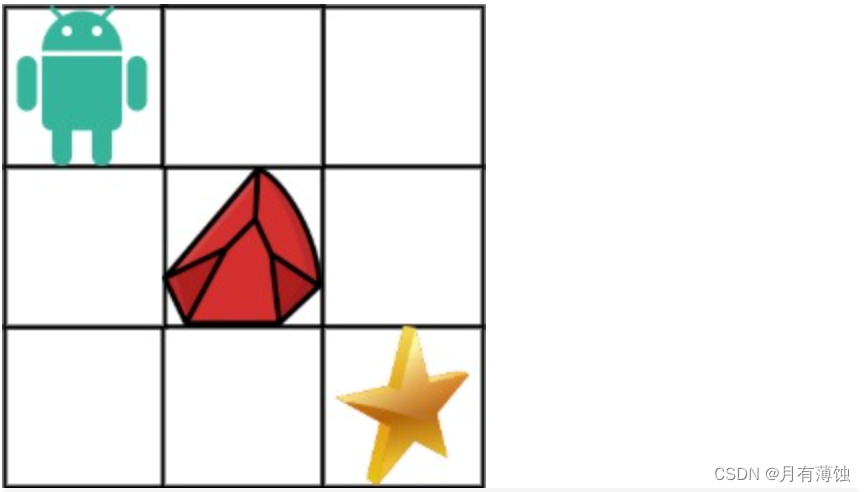
对应的dp table 如图:
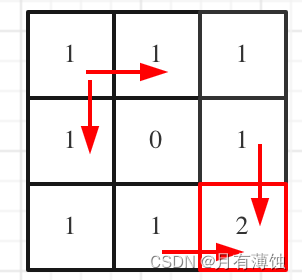
如果这个图看不懂,建议再理解⼀下递归公式,然后照着⽂章中说的遍历顺序,⾃⼰推导⼀下!
力扣提交代码
c++
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};
c语言
int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize)
{int n=obstacleGridSize;// 定义障碍物网格行数int m=obstacleGridColSize[0];// 定义障碍物网格列数//如果在起点或终点出现了障碍,直接返回0if(obstacleGrid[0][0]==1||obstacleGrid[n-1][m-1]==1) return 0;int i,j;int dp[110][110]={0};//所有元素先初始化为0//初始化dp数组for(i=0;i<n&&obstacleGrid[i][0]==0;i++) dp[i][0]=1;//第一行如果遇到障碍物,则后面为0for(j=0;j<m&&obstacleGrid[0][j]==0;j++) dp[0][j]=1;//第一列如果遇到障碍物,则后面为0for(i=1;i<n;i++){for(j=1;j<m;j++){if(obstacleGrid[i][j]==1) continue;//遇到障碍物就跳过继续dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[n-1][m-1];
}
相关文章:

不同路径 II(力扣LeetCode)动态规划
不同路径 II 题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。…...

探索深度学习:从理论到实践的全面指南
探索深度学习:从理论到实践的全面指南 摘要: 本文旨在提供一个关于深度学习的全面指南,带领读者从理论基础到实践应用全方位了解这一技术。我们将介绍深度学习的历史、基本原理、常用算法和应用场景,并通过Python代码示例和Tens…...
统计二叉树中的伪回文路径 : 用位运用来加速??
题目描述 这是 LeetCode 上的 「1457. 二叉树中的伪回文路径」 ,难度为 「中等」。 Tag : 「DFS」、「位运算」 给你一棵二叉树,每个节点的值为 1 到 9 。 我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值…...
【数据结构】树与二叉树(廿四):树搜索指定数据域的结点(算法FindTarget)
文章目录 5.3.1 树的存储结构5. 左儿子右兄弟链接结构 5.3.2 获取结点的算法1. 获取大儿子、大兄弟结点2. 搜索给定结点的父亲3. 搜索指定数据域的结点a. 算法FindTargetb. 算法解析c. 代码实现a. 使用指向指针的指针b. 直接返回找到的节点 4. 代码整合 5.3.1 树的存储结构 5.…...
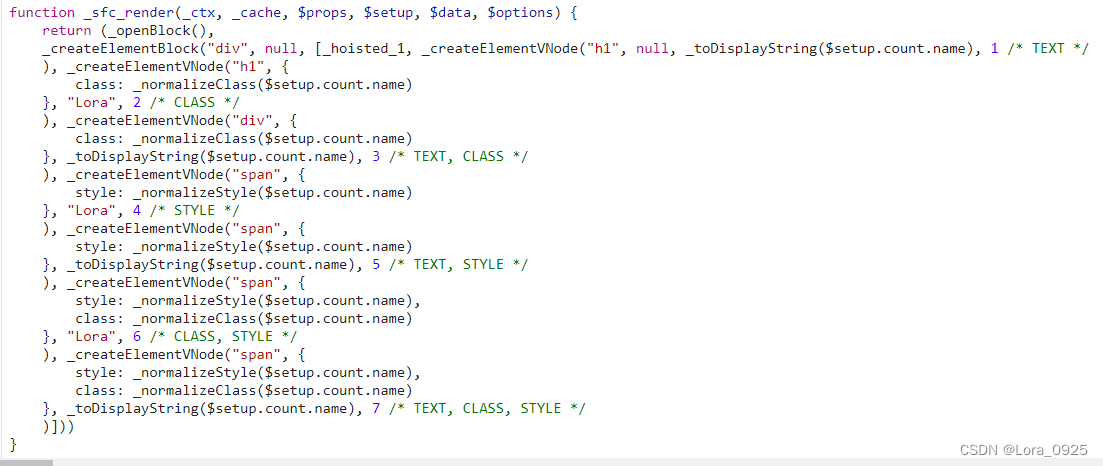
vue3怎么提升效率的?为什么vue3比vue2快?效率提升主要在哪些方面?
官方文档中说vue3在 客户端渲染效率比vue2提升了1.3~2倍, SSR渲染效率比vue2提升了2~3倍,那么究竟是怎么提升的呢? 一、静态提升 在 vue3项目中的package.json文件中,可以看到这个 vue/compiler-sfc,它是用来解析(.v…...

C语言文件操作 | 文件分类、文件打开与关闭、文件的读写、文件状态、文件删除与重命名、文件缓冲区
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和…...

从零开始的c语言日记day37——数组指针练习
一、 取地址数组储存在了*p里,里面储存的是整个数组的地址但本质也是第一个元素的地址解引用后1为4个字节所以就可以打印数组了。但一般不用这种方法 这样更方便一些 打印多维数组 如果不用这样传参,用指针传参怎么做呢? Main里函数的arr表示…...

codeforces 1851F
题目链接 题目大意:给你一个长度为n的数组a, 和一个整数k(2<n<2e5, k<30, a[i]<pow(2,k))。 任选一个x,求(a[i] ^ x) & (a[j] ^ x) 的最大值(1<i,j<n, i!j, x<pow(2,k))。 由于中间有个&,所以我们要求两个数最高…...

js把格式为YYYY-MM-DD HH:mm:ss的时间转换为UTC时间ISO 8601格式
// 要转换的日期字符串 const inputDate 2023-11-25 14:54:01; // 将日期字符串转换为Date对象 const dateObj new Date(inputDate); // 获取时间戳(毫秒) const timestamp dateObj.getTime(); // 转换格式 const outputDate new Date(tim…...

使用 Java 来读取 Excel 文件,检查每一行中的 URL,并将不符合条件的行标记为红色
-- 日、时、分、秒,这是计时的单位,惜时就应该惜日、惜时、惜分、惜秒。 用 Java 来读取 Excel 文件,检查每一行中的 URL,并将不符合条件的行标记为红色。以下是一个简单的示例,使用 Apache POI 进行 Excel 操作&#…...

雷达公式实现(matlab)
雷达公式实现 代码来源:《雷达系统分析与设计(MATLAB版)(第三版)》 function [snr] radar_eq(pt,freq,g,sigma,b,nf,loss,range) % This program implements Eq.(1.63) %% Inputs:% pt——峰值功率,W% freq——雷达中心频率,Hz% g——天线…...
CMake构建一个转换为3d tile的开源代码成功
之前CMake构建一个转换为3d tile的开源代码,生成解决方案之后,从VS2019打开; 总是报一个错误,跟 mocs_compilation_Debug.cpp 这个QT相关文件有关,它生成的obj,总是报模块计算机x64和目标计算机x86冲突&am…...

Java线程通信
线程通信 案例 package com.itheima.d4;public class ThreadTest {public static void main(String[] args) {Desk desk new Desk();//创建3个生产者线程new Thread(() -> {while (true) {desk.put();}}, "厨师1").start();new Thread(() -> {while (true) {…...
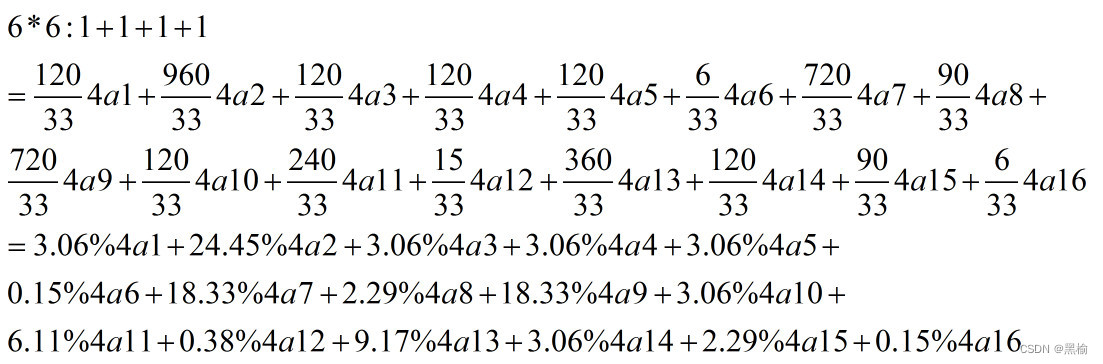
计算4人队形的最可能分布
2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 3 3 3 x 3 3 2 2 2 1 2 2 2 2 2 1 2 2 在6*6的平面上2个点随机分布,有3种分布方式,2a1,2a2,2a3,占比为1:5:1. 3 3 …...

如何解决 Java 中的 IllegalArgumentException 异常?
非法参数异常(IllegalArgumentException)的抛出是为了表明一个方法被传递了一个非法参数。该异常扩展了 RuntimeException 类,因此属于在 Java 虚拟机(JVM)运行期间可能抛出的异常。它是一种未检查异常,因此…...

Vue 双向数据绑定
之前通过v-bind来完成的数据绑定,属性值和表达式进行绑定,表达式的值发生变化了属性值也跟着发生变化。 单向数据绑定: <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>首页</titl…...

电脑开机过程中,程序的启动的顺序是怎么样的?
电脑的启动过程涉及多个步骤,程序按照特定的顺序启动。这个过程通常如下: 电源开启: 当你按下电源按钮时,电源供应器(PSU)开始向电脑的各个组件供电。 自检加电(POST): 这是电脑启动过程的第一步。在这个阶段,基本输入输出系统(BIOS)或统一可扩展固件接口(UEFI)执行…...

JSON详细教程
😊JSON详细教程 🚩JSON简介☃️JSON语法规则🔊JSON和JavaScript对象的区别 ☃️JSON数据类型字符串🔊数字🔊布尔值🔊数组🔊对象🔊Null ☃️JSON对象🔊访问JSON对象的值&a…...
DSP介绍及CCS
文章目录 CCS版本编译器CCS使用注意严禁中文 CCS的基本操作新建工程导入现有工程调整字体的大小工程界面恢复标签的使用 仿真盒小虫子进入在线Debug 仿真器芯片TMS320F28355基本介绍特性 DSP中特殊指令dsp指令中的EALLOW EDIS CCS TI官网 版本 CCS版本: CCS8.3.1…...
)
周期串(Periodic Strings)
做了我两个小时,我真的裂开 之前已经发过一次了,走在回宿舍的路上突然发现有些情况并不适用,赶紧删掉了 题目如下: 如果一个字符串可以由某个长度为k的字符串重复多次得到,则称该串以k为周期。例如:abca…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
