图论 2023.11.27
Kruskal定义不同的优先级
P3623 [APIO2008] 免费道路
给定一个无向图,其中一些边是0,其他边为1
两个不同的点之间都应该一条且仅由一条边连接
并保持刚好K条0,求是否有解决方案
n<=2e4,m<=1e5
Kruskal定义不同的优先级
思路:Kruskal先以1边优先,筛出必须要的0边
之后Kruskal先添加必须要的的0边,再以0边优先,把0边添加至k后,再添1边,最后还要检查图的连通性
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
int n, m, k, fa[N], tot, cnt;
struct edge {int u, v, w;
}e[N], ans[N];
bool cmp1(edge e1, edge e2) {return e1.w > e2.w;
}
bool cmp2(edge e1, edge e2) {return e1.w < e2.w;
}
int find(int x) {return x == fa[x] ? x:fa[x] = find(fa[x]);
}
void init() {cnt = tot = 0;for (int i = 1; i <= n; i++) fa[i] = i;
}
void check() {int tmp = find(1);for (int i = 2; i <= n; i++) {int f = find(i);if (f != tmp) {printf("no solution\n");exit(0);}tmp = f;}
}
int main()
{cin >> n >> m >> k;for (int i = 1; i <= m; i++)cin >> e[i].u >> e[i].v >> e[i].w;init();sort(e + 1, e + m + 1, cmp1); //从大到小(1边优先)for (int i = 1; i <= m; i++) {int x = find(e[i].u);int y = find(e[i].v);if (x == y) continue;fa[x] = y;if (e[i].w == 0) {tot++, e[i].w = -1; //定为必须边,下次的Kruskal此边为最高优先级}}if (tot > k) { //(1边优先)0边>k,0边优先时,0边依然>kprintf("no solution\n");return 0;}check();init(); sort(e + 1, e + m + 1, cmp2);for (int i = 1; i <= m; i++) {int f1 = find(e[i].u), f2 = find(e[i].v);if (f1 == f2) continue;if (e[i].w == 1 || tot < k) {fa[f1] = f2;if (e[i].w < 1) {tot++, e[i].w = 0;}ans[++cnt] = e[i];}}if (tot < k) {printf("no solution\n");return 0;}check();for (int i = 1; i <= cnt; i++) {printf("%d %d %d\n", ans[i].u, ans[i].v, ans[i].w);}return 0;
}几何联通
P3958 [NOIP2017 提高组] 奶酪
给定一个它的高度为 h,它的长度和宽度我们可以认为是无限大的奶酪,有n个空洞坐标为(x,y,z)
统一半径为r,能否利用已有的空洞跑 到奶酪的上表面去
深度优先搜索,不需要回溯,进入和出来判断只需看z-r,z+r和0,h的比较
n<=1e3,h,r<=1e9
#include<iostream>
#include<algorithm>
#include<string.h>
#include<cstring>
#include<math.h>
using namespace std;
const int N = 1e3 + 10;
int n;
double h, r;
int vis[N];
int ans;
struct cir {double x, y, z;bool operator <(const cir& c)const { //按从低到高return z < c.z; }
}a[N];
double dist(double x1, double y1, double z1, double x2, double y2, double z2){return sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1) + (z2 - z1) * (z2 - z1));
}
void dfs(int now) {if (ans) return;if (a[now].z + r>= h) {ans = 1;return;}vis[now] = 1;for (int i = 1; i <= n; i++) {if (vis[i]) continue;if (dist(a[now].x, a[now].y, a[now].z, a[i].x, a[i].y, a[i].z) > 2 * r) continue;dfs(i);}
}
void solve() {memset(vis, 0, sizeof(vis));ans = 0;cin >> n >> h >> r;for (int i = 1; i <=n; i++) {cin >> a[i].x >> a[i].y >> a[i].z;}sort(a + 1, a + 1 + n);for (int i = 1; i <= n; i++) {if (a[i].z- r <= 0) {dfs(i); //深搜}}if (!ans) {cout << "No" << '\n';}else {cout << "Yes" << '\n';}
}
int main()
{int t;cin >> t;while (t--) solve();
}二维联通
P2498[SDOI2012] 拯救小云公主
给定一个row行line列大小的矩阵,给定n个boss的位置,需要从左下角,到达右上角
找一条路径使到距离boss的最短距离最远,输出最远距离
n<=3000
思路:小数二分最远距离,boss点作为圆心, 参考奶酪
左边界或上边界通过这些洞和右边界或下边界联通时,问题无解
#include<iostream>
#include<cstring>
#include<math.h>
#include<queue>
using namespace std;
int dis[3001][3001];
int x[3001], y[3001];
int getdis(int x1, int y1, int x2, int y2) {return pow(x1 - x2, 2) + pow(y1 - y2, 2);
}
bool able(int d, double r) {return r * r * 4 > d;
}
int row, line, n;
queue<int>q;
bool vis[3001];
bool bfs(double r) {memset(vis, 0, sizeof(vis));while (!q.empty())q.pop();for (int i = 1; i <= n; i++) {if (row - y[i] < r||x[i]<r) { // 左下角(row, 0)出发通过这些圆q.push(i), vis[i] = 1;}}while (!q.empty()) {int p = q.front();q.pop();if (y[p] < r|| line - x[p] < r) { //右上角(0,line)通过这些圆return 0;}for (int i = 1; i <= n; i++)if (!vis[i] && able(dis[p][i], r)) { vis[i] = 1, q.push(i);}}return 1;
}
int main() {cin >> n >> line >> row;line--; row--;for (int i = 1; i <= n; i++) {cin >> x[i] >> y[i];x[i]--;y[i]--;}for (int i = 1; i <= n; i++)for (int j = 1; j < i; j++)dis[i][j] = dis[j][i] = getdis(x[i], y[i], x[j], y[j]);double l = 0, r = min(row, line), mid;for (int i = 1; i <= 60; i++) {mid = (l + r) / 2;if (bfs(mid))l = mid;else r = mid;}printf("%.2lf\n", l);return 0;
}视为T在S之间滑动,转换为拓扑图目标所有窗口匹配,即度数为0 (atcoder 329 E)
给定一个长度为n字符串S,长度为m的字符串T
将长度为n字符串全是#变成S,操作:用T替换S的部分区间
n<=2e5,m<=5
思路:视为T在S之间滑动,于是有n-m+1的窗口
转换为拓扑图:入度为每个窗口不匹配的数量,一旦为0完全匹配,边为该窗口不匹配的字符,编号为(窗口编号i相连字符编号i+j)
之后拓扑,ans倒序后得到操作的顺序,目标为所有窗口完全匹配因为(视为T在S之间滑动)
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>#include<unordered_map>#include<unordered_set>#include<bitset>#include<array>using namespace std;#define endl '\n'#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)#define int long long#define int128 __int128_t#define ll long long#define ld long doubletypedef unsigned long long ull ;#define fr(i,l,r) for(int i=l;i<=r;i++)#define fer(i,x) for(int i=e.head[x];i;i=e.next[i])#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondtypedef pair<int,int> pr;const int N = 1e6+10;const int mod=998244353,inf=1e18;int n,m;int a[N];map<int,int>mp;void solve(){cin>>n>>m;string s,t;cin>>s>>t;vector<int>in(n+1,m);vector<vector<int>>e(n+1); //边 queue<int>q;for(int i=0;i<n-m+1;i++){for(int j=0;j<m;j++){if(s[i+j]==t[j]){in[i]--;if(in[i]==0){ //完全与t对应q.push(i);}}else{e[i+j].push_back(i); }}}vector<int>ans;while(!q.empty()){int u=q.front();q.pop();ans.push_back(u);for(int i=0;i<m;i++){if(mp[u+i]){continue;}mp[u+i]=1;for(auto it:e[u+i]){in[it]--;if(in[it]==0){q.push(it);}}}}reverse(ans.begin(),ans.end()); //每一次操作位置if(ans.size()<n-m+1){cout<<"No"<<'\n';}else{cout<<"Yes"<<'\n';}}signed main(){ios;int t=1;// cin>>t;while(t--) solve();return 0;}相关文章:

图论 2023.11.27
Kruskal定义不同的优先级 P3623 [APIO2008] 免费道路 给定一个无向图,其中一些边是0,其他边为1 两个不同的点之间都应该一条且仅由一条边连接 并保持刚好K条0,求是否有解决方案 n<2e4,m<1e5 Kruskal定义不同的优先级 思路:…...
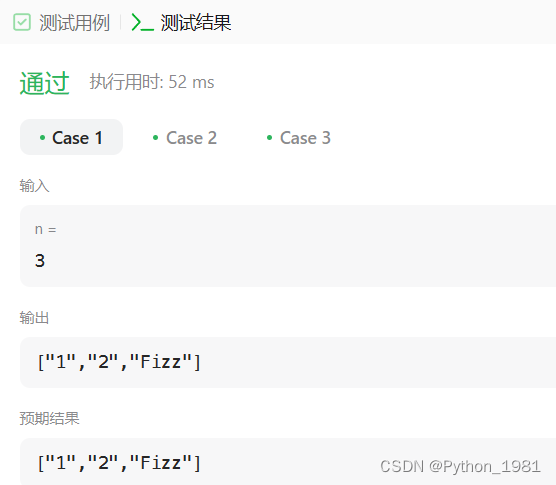
蓝桥杯day02——Fizz Buzz
1、题目 给你一个整数 n ,找出从 1 到 n 各个整数的 Fizz Buzz 表示,并用字符串数组 answer(下标从 1 开始)返回结果,其中: answer[i] "FizzBuzz" 如果 i 同时是 3 和 5 的倍数。answer[i] &…...
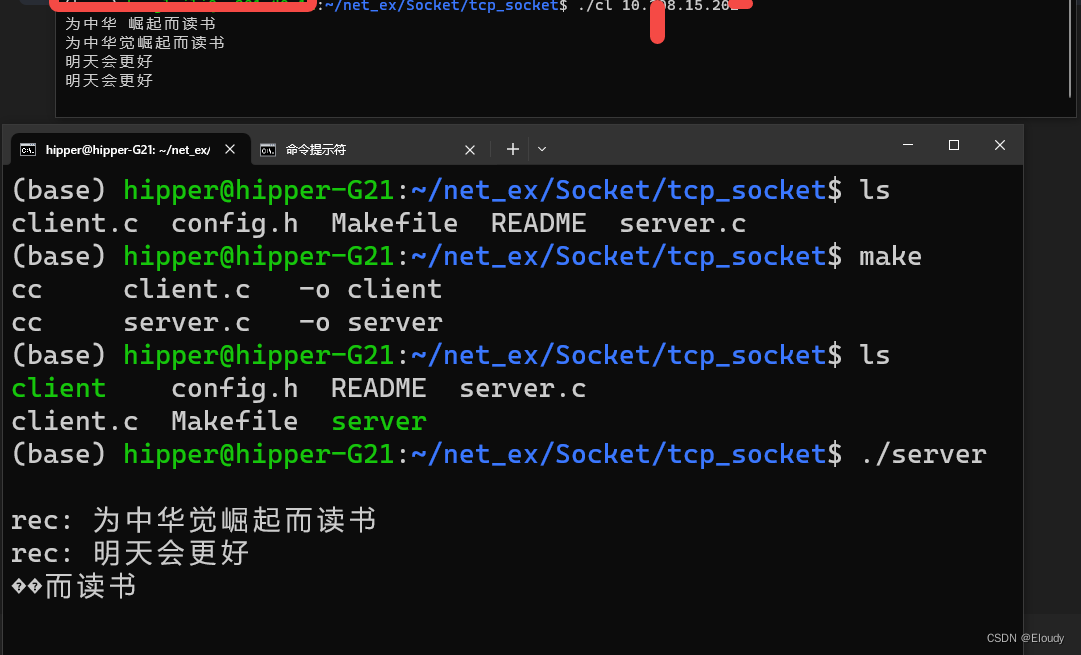
socket 一个完整的不错的示例
从客户端向服务器端发送信息时,在服务器端有打印显示; 检测环境常用,备份一下 0,公共头文件代码 //config.h#include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/socket.h> #inc…...

第10关:基数排序
任务要求参考答案问答98 任务描述相关知识 基数排序算法编程要求测试说明 任务描述 本关任务:实现基数排序算法,并将乱序数列变成升序。 相关知识 为了完成本关任务,你需要掌握:1.基数排序算法。 基数排序算法 基数排序是按…...

torch::和at:: factory function的差別
torch::和at:: factory function的差別 前言torch::autograd::THPVariable_randtorch::rand_symintat::rand_symintdemotorch命名空間at命名空間 前言 >>> import torch >>> a torch.rand(3, 4) >>> a.requires_grad False >>> a torch…...

与珎同行录-开篇-231129
与珎同行录-开篇 珎就是对陪伴并帮助我写代码的AI的昵称 能不能读懂这个绕口令问题呢? 连续的椎体的相邻椎体质心的相邻质心的质心作为当前质心所在的椎体的质心, 该质心的方向代表该椎体的上下方向 如何代码实现呢? 还是没看懂…好吧最终的算法是:...

linux logrotate日志轮询设置案例一
1.编辑/etc/logrotate.conf文件,添加如下配置,并保存 /var/log/ztj.log {missingokhourlycreate 644 root rootsharedscriptspostrotateif [ -f /var/run/syslogd.pid ];then/bin/kill -HUP $(/bin/cat /var/run/syslogd.pid) >/dev/null 2>&…...

Android 12.0 禁用adb reboot recovery命令实现正常重启功能
1.前言 在12.0的系统rom定制化开发中,在定制recovery模块的时候,由于产品开发需要要求禁用recovery的相关功能,比如在通过adb命令的 adb reboot recovery的方式进入recovery也需要实现禁用,所以就需要了解相关进入recovery流程来禁用该功能 2.禁用adb reboot recovery命令…...
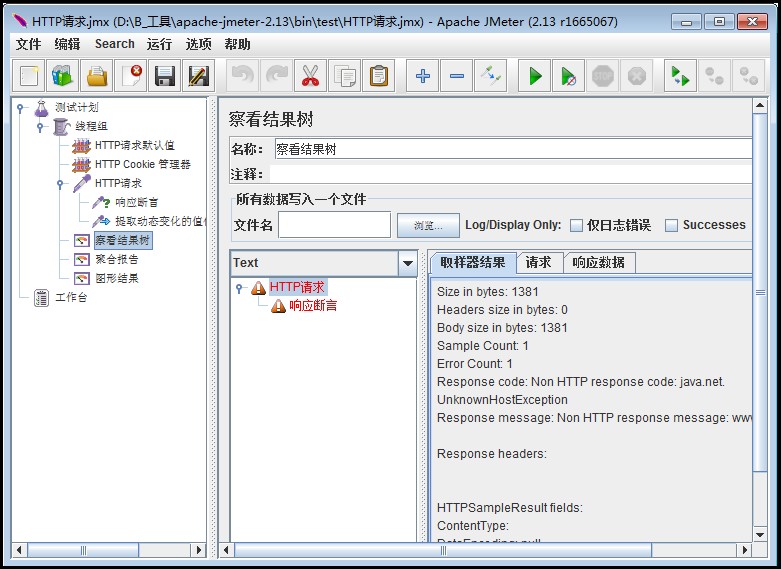
使用Jmeter进行http接口测试
前言: 本文主要针对http接口进行测试,使用Jmeter工具实现。 Jmter工具设计之初是用于做性能测试的,它在实现对各种接口的调用方面已经做的比较成熟,因此,本次直接使用Jmeter工具来完成对Http接口的测试。 一、开发接口…...
:ION 内存管理器——cma heap)
Linux内存管理(六十三):ION 内存管理器——cma heap
源码基于:Linux 5.4 约定: 芯片架构:ARM64内存架构:UMACONFIG_ARM64_VA_BITS:39CONFIG_ARM64_PAGE_SHIFT:12CONFIG_PGTABLE_LEVELS :3ION 系列博文: ION 总篇ION —— cma heapION —— system heap0. 前言 ION 是 Google 在 Android 4.0 中引入,目的主要是通过在硬件…...

条形码格式
条形码格式 简述EAN码EAN-13EAN-8 UPC码UPC-AUPC-E CODE128 简述 EAN码 EAN码(European Article Number)是国际物品编码协会制定的一种全球通用的商用条码。EAN码分为:标准版(EAN-13) 和 缩短版(EAN-8&am…...
)
Java通过Redis进行延时队列,定时发布消息(根据用户选择时间进行发布)
前言 目前很多产品都用到过定时发布或者定时推送等功能,定时推送有两种定义,一种是后台自己有相关规则,通过定时器设置好相应的时间进行推送(例如定时任务框架QuartZ、xxl-job等实现,或者通过springboot自带定时任务Scheduled注解等实现)&am…...
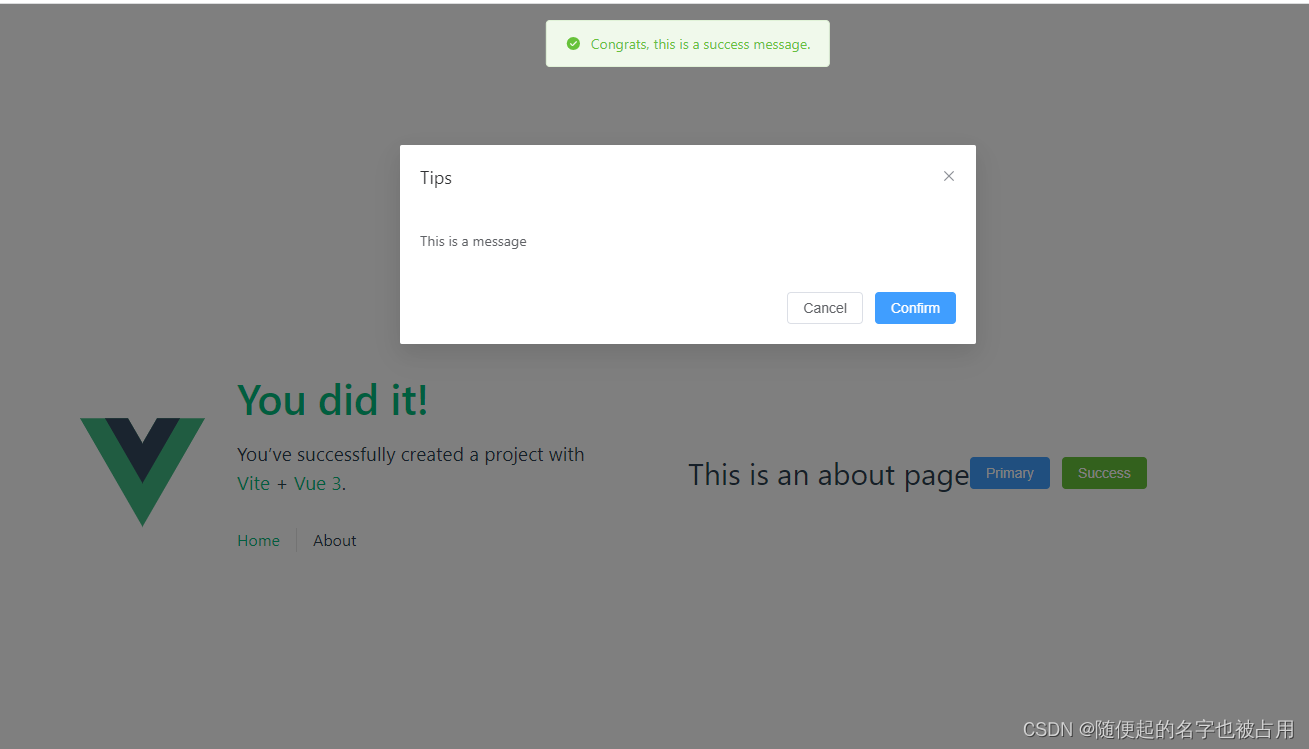
从 0 搭建 Vite 3 + Vue 3 Js版 前端工程化项目
之前分享过一篇vue3+ts+vite构建工程化项目的文章,针对小的开发团队追求开发速度,不想使用ts想继续使用js,所以就记录一下从0搭建一个vite+vue3+js的前端项目,做记录分享。 技术栈 Vite 3 - 构建工具 Vue 3 Vue Router - 官方路由管理器 Pinia - Vue Store你也可以选择vue…...

【论文阅读笔记】Smil: Multimodal learning with severely missing modality
Ma M, Ren J, Zhao L, et al. Smil: Multimodal learning with severely missing modality[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2021, 35(3): 2302-2310.[开源] 本文的核心思想是探讨和解决多模态学习中的一个重要问题:在训练和测…...
在Windows系统上安装git-Git的过程记录
01-上git的官网下载git的windows安装版本 下载页面链接: https://git-scm.com/downloads 选择Standalone Installer的版本进行下载: 这里给大家一全git-2.43.0的百度网盘下载链接: https://pan.baidu.com/s/11HwNTCZmtSWj0VG2x60HIA?pwdut…...

qt QString常用方法
1. QString 尾部拼接,尾部插入字符.调用append()函数.同时,QString字符串直接用加号 也可以进行拼接. QString s "我的女神";s s "刘亦菲";s "最近可好?";s.append("你跑哪儿去了?");//拼接结果: 我的女神刘亦菲最近可好?你跑…...

吴恩达《机器学习》10-6-10-7:学习曲线、决定下一步做什么
一、学习曲线 1. 学习曲线概述 学习曲线将训练集误差和交叉验证集误差作为训练集实例数量(m)的函数绘制而成。这意味着从较少的数据开始,逐渐增加训练集的实例数量。该方法的核心思想在于,当训练较少数据时,模型可能…...
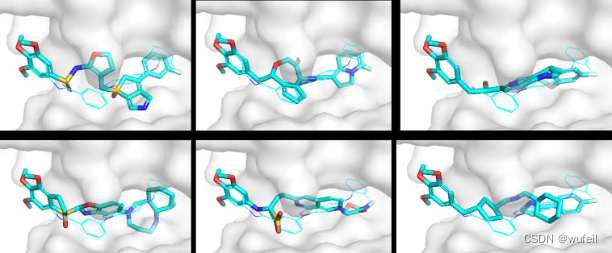
分子骨架跃迁工具-DiffHopp 评测
一、文章背景介绍 DiffHopp模型发表在ICML 2023 Workshop on Computational Biology(简称:2023 ICML-WCB)上的文章。第一作者是剑桥计算机系的Jos Torge。 DiffHopp是一个专门针对骨架跃迁任务而训练的E3等变条件扩散模型。此外,…...

MySQL双主双从数据库集群搭建
1 引言 在之前的文章中提到过相关搭建方法,具体请参考《MySQL主从数据库搭建》这篇文章,本文主要讲述双主双从,双主多从集群的搭建方式。 这里要问一个问题,为什么MySQL要搭建数据库集群呢?我想应该有以下几点原因&…...
vue实现动态路由菜单!!!
目录 总结一、步骤1.编写静态路由编写router.jsmain.js注册 2.编写permisstions.js权限文件编写permisstions.jsaxios封装的APIstore.js状态库system.js Axios-APIrequest.js axios请求实例封装 3.编写菜单树组件MenuTree.vue 4.主页中使用菜单树组件 总结 递归处理后端响应的…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

NineData数据库DevOps功能全面支持百度智能云向量数据库 VectorDB,助力企业 AI 应用高效落地
NineData 的数据库 DevOps 解决方案已完成对百度智能云向量数据库 VectorDB 的全链路适配,成为国内首批提供 VectorDB 原生操作能力的服务商。此次合作聚焦 AI 开发核心场景,通过标准化 SQL 工作台与细粒度权限管控两大能力,助力企业安全高效…...
